湖北省宜昌市部分示范高中教学协作体2018-2019学年高二上学期期中理科数学试题

宜昌市部分示范高中教学协作体2019年秋高二期中联考数 学（全卷满分：150分 考试用时：150分钟）一、选择题:本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1、已知两点()()1,2,3,4A B -，则直线AB 的斜率为A. 2B. 21-C.21D. 2-2、数列3，5，9，17，33，…的一个通项公式n a 可以为( )A. 21n +B. 12+nC.12-nD. 121n +-3、在等比数列{}n a 中，12,34321=+=+a a a a ，则65a a +的值为 ( )A. 18B. 21C. 24D. 484、过点()3,1-P 且倾斜角为 30的直线方程为（ ）A. 03433=+-y xB. 0323=+-y xC. 03233=+-y xD. 03=-y x5、已知数列{}n a 的前n 项和n n S n -=2，则=5a ( )A. 6B. 8C. 12D. 206、已知圆过()()()1,2,1,0,3,0A B C --三点，则圆的方程是（ ）A. 09422=--+x y xB. 05422=-++x y xC. 07222=--+x y xD. 03222=-++x y x7、在等差数列{}n a 中，若76,a a 是方程0132=-+x x 的两根，则{}n a 的前12项的和为( )A. 6B. 18C. -18D. -68、不论m 为何实数，直线()0121=+---m y x m 恒过定点（ ）A.()1,1-B.()1,2-C.()1,2--D. ()1,19、已知数列{}n a 满足3,211-==-+a a a n n ，则=+++521a a a ( )A. 13B. 8C. 5D. 2010、已知数列{}n a 满足nn n a a a 2,211+==+，则n a =（ ）A.2nB. n 2C. 121+-nD.221-+n11、已知()()0,1,4,2B A ，动点P 在直线1-=x 上，当PB PA +取最小值时，则点P 的坐标为（ ）A.⎪⎭⎫ ⎝⎛-58,1 B. ⎪⎭⎫ ⎝⎛-521,1 C. ()2,1-D. ()1,1-12、直线01=-+ay ax 与圆0122222=+-+a y a x a 有公共点()00,y x ，则00y x 的最大值为（ ）A.41- B.34C.94D. 2二、填空题：本大题共4小题，每小题5分，共20分. 13、已知直线013:=-+y x l ，则直线l 的倾斜角为______．14、已知点()()()2,3,2,1,,2A B C x --，若A 、B 、C 三点共线，则x 的值为______．15、已知1，a,b,c,4成等比数列，则b=______．16、已知圆012:22=--+x y x C ，以点1,12⎛⎫⎪⎝⎭为中点的弦所在的直线方程是______．三、解答题：解答题应写出文字说明，证明过程或演算步骤. 17、（本小题满分10分） 已知直线l 过点()2,3P ．⑴若直线l 与052=++y x 平行，求直线l 的方程; ⑵若直线l 在两坐标轴上的截距相等，求直线l 的方程．18、（本小题满分12分）在等差数列{}n a 中，13,5543=+=a a a （1）求数列{}n a 的通项公式； （2）设n b n a n +=-22，求数列{}n b 的前n 项和n S ．19、（本小题满分12分）已知递增等比数列{}n a 满足：13,332==S a⑴求{}n a 的通项公式及前n 项和n S ； ⑵设()13log 11+⋅+=n n a n b ，求数列{}n b 的前n 项和n T．20、（本小题满分12分）已知曲线方程042:22=+--+m y x y x C .⑴ 若曲线C 表示圆，求m 的取值范围；⑵ 当m=4时，求圆心和半径；⑶当m=4时，若圆C 与直线04:=-+y x l 错误！未找到引用源。

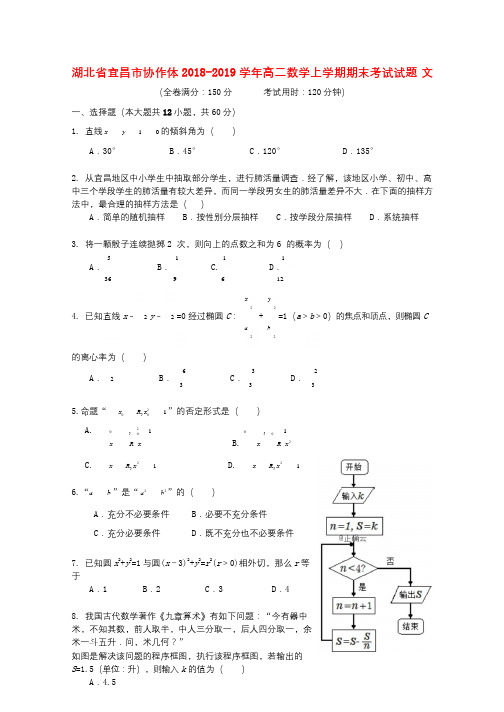
湖北省宜昌市协作体 2018-2019学年高二数学上学期期末考试试题 文（全卷满分：150分考试用时：120分钟）一、选择题（本大题共 12小题，共 60分） 1. 直线 xy 1 0 的倾斜角为（ ）A ．30°B ．45°C ．120°D ．135°2. 从宜昌地区中小学生中抽取部分学生，进行肺活量调查．经了解，该地区小学、初中、高 中三个学段学生的肺活量有较大差异，而同一学段男女生的肺活量差异不大．在下面的抽样方 法中，最合理的抽样方法是（ ）A ．简单的随机抽样B ．按性别分层抽样C ．按学段分层抽样D ．系统抽样 3. 将一颗骰子连续抛掷 2次，则向上的点数之和为 6的概率为（ ）51 1 1A ．B ．C.D ．36 9612xy224. 已知直线 x ﹣ 2 y ﹣ 2 =0经过椭圆 C ： + =1（a ＞b ＞0）的焦点和顶点，则椭圆 Cab22的离心率为（ ） 63A ． 2B ．C ．D ．3 32 35.命题“x 0 R , x 02 1”的否定形式是（）A., 02 1 0, 0 1 xR xB. x R x 2C. x R , x 2 1D.x R , x 216.“ab ”是“ a 2 b 2 ”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7. 已知圆 x 2+y 2=1与圆(x －3)2+y 2=r 2(r ＞0)相外切，那么 r 等 于A ．1B ．2C ．3D ．4 8. 我国古代数学著作《九章算术》有如下问题：“今有器中 米，不知其数，前人取半，中人三分取一，后人四分取一，余 米一斗五升．问，米几何？”1B ．6C ．7.5D ．9x 3y 6 09. 已知实数 x ， y 满足 x y2 4 02x 3y 12 0，则 z x y 的最小值是（ ） 2 A ． 6B ． 4C ．D ．05xy22410. 若椭圆的离心率为 ，则 k 的值为( )194 k51919A ．－21B ．21C ．－ 或 21D. 或 21252511. 若圆 C ：x 2＋y 2－4x －4y －10＝0上至少有三个不同的点到直线 l ：x －y ＋c ＝0的距离为 2 2，则 c 的取值范围是（ ）A ．[－2,2]B ．(－2 2，2 2)C ．[－2 2，2 2]D ．(－2,2)xy2 2 221( 0)AF BFa b12. 椭圆上一点A 关于原点的对称点为B ，F 为其右焦点，若，ab设ABF, 且,，则该椭圆离心率的取值范围为 （ ）12 4,1 A. B.C.D.2 23 3二、填空题（本大题共 4 小题，共 20 分）13. 从某班抽取 5名学生测量身高（单位：cm ），得到的数据为 160，162，159，160，159， 则该组数据的方差 s 2=______ ．114. 在区间(0,1)内任取两个实数，则这两个实数的和大于 的概率为______ ．3x215. 已知 P 是椭圆 y 2 1上的一点， 是椭圆的两个焦点，当 F PF时，则F 1, F 21234PF F 1 2的面积为______．216. 在平面直角坐标系XOY中，圆C的方程为x2＋y2－8x＋15＝0，若直线y＝kx－2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是______ ．三、解答题（本大题共6小题，共70分）17.（本小题10分）已知命题p：函数f（x）=lg（x2+mx+m）的定义域为R，命题q：函数g （x）=x2﹣2x﹣1在[m，+∞）上是增函数．（1）若p为真，求m的范围；（2）若“p∨q”为真命题，“p∧q”为假命题，求m的取值范围．18.（本小题12分）已知直线l的方程为2x y10.（1）求过点A（3，2），且与直线l垂直的直线l1的方程；（2）若直线l 2与直线l平行，且点P（3，0）到直线l2的距离为5，求直线l2的的方程.19.（本小题12分）宜昌车天地关于某品牌汽车的使用年限x（年）和所支出的维修费用y（千元）由如表的统计资料：x 2 3 4 5 6y 2.1 3.4 5.9 6.6 7.0（1）画出散点图并判断使用年限与所支出的维修费用是否线性相关；如果线性相关，求回归直线方程；（2）若使用超过8年，维修费用超过1.5万元时，车主将处理掉该车，估计第10年年底时，车主是否会处理掉该车？n n(x x)(y y)x y nx yi i i i）（b1 1n ni i320 （本小题12分）对宜昌某校高二年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下：分组频数频率10,1510 0.2515,2024 n20,25m p25,30 2 0.05合计M 1（1）求出表中M、P及图中a的值；（2）若该校高二学生有240人，试估计该校高二学生参加社区服务的次数在区间10,15内的人数；（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加25,30内的概率.社区服务次数在区间21 （本小题12分）已知以点C为圆心的圆经过点A(-1,0)和B(3,4),且圆心在直线x+3y-15=0 上.(1)求圆C的方程.(2)设点P在圆C上,求△PAB的面积的最大值.x y2222、（本小题12分）已知和是椭圆221(a b0)的两个焦点，F1(1,0)2(1,0)Fa b3P(1,)且点在椭圆C上．2（1）求椭圆C的方程；（2）直线l:y kx m（m＞0）与椭圆C有且仅有一个公共点，且与x轴和y轴分别交于点M，N，当△OMN面积取最小值时，求此时直线l的方程．6宜昌市部分示范高中教学协作体 2018年秋期末联考高二（文科）数学参考答案 题号 1 2 3 4 5 6 7 8 9 10 1112答案 DC AB D D BBBCAB17 13141516184317.解：（1）若 p 为真，x 2+mx+m ＞0恒成立，…（1分）所以△=m 2﹣4m ＜0，----------2分 所以 0＜m ＜4．-------------------------------4分（2）因为函数 g （x ）=x 2﹣2x ﹣1 的图象是开口向上，对称轴为 x=1的抛物线， 所以，若 q 为真，则 m ≥1．-------------------------------6分 若 p ∨q 为真，p ∧q 为假，则 p ，q 中一真一假； ∴或，-------------------------------8分所以 m 的取值范围为{m|0＜m ＜1或 m ≥4}．-------------------------------10分 18. 解：（1）设与直线 l ：2x -y +1=0垂直的直线l 1 的方程为：x +2y +m =0，-------------------------2分把点 A （3，2）代入可得，3+2×2+m =0，解得 m =-7．-------------------------------4分∴过点 A （3，2）且与直线 l 垂直的直线l 1 方程为：x +2y -7=0；----------------------6分（2）设与直线 l ：2x -y +1=0平行的直线l 2 的方程为：2x -y +c =0， ----------------------------8分∵点 P （3，0）到直线l 2 的距离为 5 ．23 c 5∴，解得 c =-1或2 1 2 2-11．-----------------------------------------------10分∴直线l 2 方程为：2x -y -1=0或2x -y -11=0．-------------------------------------------12分 19.解：（1）作出散点图如图：由散点图可知是线性相关的-------------------------------2分列表如下：5x y5x yi i113545b 1.3i1计算得：，5229054x5x2ii1于是：a y b x5 1.340.2，即得回归直线方程为y 1.3x0.2-------------------------------6分（2）把x10代入回归方程y 1.3x0.2，得y12.8，因此，估计使用10年维修费用是12.8千元，即维修费用是1.28万元，因为维修费用低于1.5万元，所以车主不会处理该车．-------------------------------12 分1020.解：（1）由分组[10,15)内的频数是10，频率是0.25知，0.25，所以MM40. ………2分因为频数之和为40，所以1024m240，m4. …………………3分m4因为a是对应分组[15,20)的频率与组距的商，所以240.12. ……………6分a405（2）因为该校高二学生有240人，分组[10,15)内的频率是0.25，8所以估计该校高二学生参加社区服务的次数在此区间内的人数为 60 人. ……………8分 （3）这个样本参加社区服务的次数不少于 20次的学生共有 m 2 6人， …………………9分 设在区间[20, 25)内的人为a a a a，在区间[25,30)内的人为1, 2 , 3,4b b .1, 2则任选 2 人共有 (a 1,a 2 ), (a 1,a 3 ), (a 1,a 4 ), (a 1,b 1), (a 1,b 2 ), (a 2 ,a 3 ), (a 2 ,a 4 ), (a 2 ,b 1),(a ,b ), (a ,a ) ， (a ,b ), (a ,b ), (a ,b ), (a ,b ), (b ,b )15种情22343132414212况， …………………11分而两人都在[25,30)内只能是b b 一种， 所以所求概率为1, 21 14P1 .……………………12分15 1521. (1)依题意所求圆的圆心 C 为 AB 的垂直平分线和直线 x+3y-15=0的交点, 因为 AB 中点为(1,2),斜率为 1,所以 AB 的垂直平分线方程为 y-2=-(x-1), 即 y=-x+3, ……………………2分 联立 解得即圆心(-3,6), ……………………4分 半径 r===2.所以所求圆方程为(x+3)2+(y-6)2=40. ……………………6分 (2)|AB|==4,圆心到 AB 的距离为 d=4 ,……………………8分P 到 AB 距离的最大值为 d+r=4 +2,……………………10分所以△PAB 面积的最大值为 ×4×(4+2)=16+8.……………………12分xy22F 1(1, 0)2(1, 0)F22.（1）∵和是椭圆的两个焦点，且点3 P (1, )2∴依题意，c1，又2(11)2(30)234，故．---------------------2a a222分9由b2c2a2得b2=3．-----------------------------------------------------------3分x y22故所求椭圆C的方程为1．-----------------------------------------------443分22x y143（2）由，消y得（4k2+3）x2+8kmx+4m2-12=0，y kx m由直线l与椭圆C仅有一个公共点知，△=64k2m2-4（4k2+3）（4m2-12）=0，整理得m2=4k2+3．-----------------------------6分m由条件可得k≠0，M(,0)，N（0，m）．k所以．①------------------------------8分将m2=4k2+3代入①，得．因为|k|＞0，所以，-------------------------------10分34k当且仅当，则，即时等号成立，S△OMN有最小值．-----11分k因为m2=4k2+3，所以m2=6，又m＞0，解得．故所求直线方程为或．----------------------------12分10宜昌市部分示范高中教学协作体2018年秋期末联考高二（文科）数学命题双向细目表题号题型分值考查知识点能力要求试题难度试题来源1 选择 5 直线：直线的倾斜角掌握0.9 资料2 选择 5 统计：抽样方法掌握0.8 改编3 选择 5 概率：古典概率应用0.85 改编4 选择5 椭圆：椭圆离心率掌握0.8 试卷5 选择 5 直线：点到直线的距离公式应用0.8 试卷6 选择 5 逻辑：充要条件理解0.8 改编7 选择 5 圆：两圆位置关系应用0.7 资料8 选择 5 程序框图应用0.65 资料9 选择 5 线性规划综合0.7 资料10 选择 5 椭圆应用0.6 改编11 选择 5 直线与圆应用0.5 改编12 选择 5 椭圆：椭圆的离心率范围综合0.4 改编13 填空 5 统计：均值，方差掌握0.85 改编14 填空 5 概率：几何概型应用0.7 资料15 填空 5 椭圆：焦点三角形应用0.55 书本改编16 填空 5 圆：与圆相关的最值理解0.3 书本重组17 解答10 逻辑：逻辑联结词应用0.8 改编18 解答12 直线：点关于直线对称等掌握0.7 书本改编19 解答12 统计：回归方程综合0.6 试卷20 解答12 概率：古典概型综合0.6 改编21 解答12 圆：圆的标准方程，直线与圆的位置关系综合0.5 改编22 解答12 椭圆：标准方程，综合应用应用0.25 试卷。

宜昌市部分示范高中教学协作体2018年秋期中联考高二物理（全卷满分：100分考试用时：90分钟）一、选择题（本题共12小题，每小题4分，共48分。

其中1～8题为单选题，9～12题为多选题，多选题全部选对的得4分，选对但不全的得2分，有选错的得0分）1．关于电场强度的下列说法中，正确的是A．电场强度与试探电荷所受电场力成正比B．试探电荷的电荷量越大，电场强度越大C．电场强度的方向就是试探电荷所受电场力的方向D．电场强度是电场本身的性质，与试探电荷的电量及其所受电场力大小无关2．下列公式中，既适用于点电荷产生的静电场，也适用于匀强电场的有①场强FEq=②场强UEd=③场强2QE kr=④电场力做功W qU=A．①③ B．①④ C．②③ D．②④3．如图所示，在匀强电场中有a、b、c、d四点，它们处于同一圆周上，且ac、bd分别是圆的直径．已知a、b、c三点的电势分别为φa=9V，φb=15V，φc=18V，则d 点的电势为A．4VB．8VC．12VD．16V4．如图所示，用静电计可以测量已充电的平行板电容器两极板之间的电势差U，现使B板带正电，则下列判断正确的是A．若将玻璃板插入两板之间，则静电计指针张角变大B．增大两极板之间的距离，静电计指针张角变大C．将A板稍微上移，静电计指针张角将变小D．减小两极板之间的距离，静电计指针张角变大5．一个电流表的满偏电流I g=1mA．内阻为500Ω，要把它改装成一个量程为10V的电压表，则应在电流表上A．串联一个10kΩ的电阻 B．并联一个10kΩ的电阻C．串联一个9.5kΩ的电阻 D．并联一个9.5kΩ的电阻6．用伏安法测电阻R，按（甲）图测得的结果为R1，按（乙）图测得的结果为R2，若电阻的真实值为R Z，则下列关系正确的是A．R1 > R Z > R2B．R1 < R Z < R2C．R Z > R1，R Z > R2D．R1 = R Z = R27．人从高处跳到低处时，为了安全，一般都是脚触地后，顺势下蹲，这样做是为了A．减小地面对人的冲量的大小B．增大人与地面的压强，这样人触地更平稳C．增大人与地面的作用时间，减小地面对人的作用力 D．使人的动量变化量减小8．如图所示，小车AB放在光滑水平面上，A端固定一个轻弹簧，B端粘有油泥，AB总质量为M，质量为m的木块C放在小车上，用细绳连接于小车的A端并使弹簧压缩，开始时AB和C都静止，当突然烧断细绳时，C被释放，C离开弹簧向B端冲去，并跟B端油泥粘在一起，忽略一切摩擦，以下说法正确的是A．弹簧伸长过程中C向右运动，同时AB也向右运动B．C与B碰前，C与AB的速率之比为m:MC．C与油泥粘在一起后，AB继续向右运动D．C与油泥粘在一起后，AB立即停止运动9．如图所示，AC、BD为圆的两条互相垂直的直径，圆心为O，半径为r，将带等电荷量的正、负点电荷放在圆周上，它们的位置关于AC对称，＋q与O点的连线和OC夹角为30°，下列说法正确的是A．A、C两点的电势关系是φA＝φCB．B、D两点的电势关系是φB＝φDC ． O 点的场强大小为kq r2 D ． O 点的场强大小为3kq r210．如图所示，AB 、CD 为一圆的两条直径，且互相垂直，O 点为圆心。

2018年秋季湖北省重点高中联考协作体期中考试 高二理科数学(B)试卷参考答案及评分细则一.选择题:13. 17 14. 4π15. 8 16. ④ 三.解答题:17. (1)因为命题p 为真，则对数的真数－2t 2＋7t －5>0，解得1<t <52.所以实数t 的取值范围是⎝ ⎛⎭⎪⎫1，52 (5)分(2)因为p 是q的充分不必要条件，所以⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫t ⎪⎪⎪1<t <52是不等式t 2－(a ＋3)t ＋a＋2<0的解集的真子集．法一 因为方程t 2－(a ＋3)t ＋a ＋2＝0的两根为1和a ＋2， 所以只需a ＋2>52，解得a >12又1a ≠.即实数a 的取值范围为112a a >≠且.法二 令f (t )＝t 2－(a ＋3)t ＋a ＋2，因为f (1)＝0，所以只需52f ⎛⎫⎪⎝⎭<0，解得a >12.即实数a 的取值范围为112a a >≠且.……10分18. 解：⑴1111MN MA A B B N =++1111133BA AB B C =++ 11111()()33333=-++-=++c a a b a a b c .…………………………6分 ⑵2()222++=+++⋅+⋅+⋅222a b c a b c a b b c c a111110211211522=++++⨯⨯⨯+⨯⨯⨯=，||++a b c，1||||33MN =++=a b c .………………………12分 19. 解：易知此弦所在直线的斜率存在,所以设斜率为k,A(x 1,y 1),B(x 2,y 2),则221122221,421,42x y x y +=+=⎧⎪⎨⎪⎩相减得,12121212()()()()042x x x x y y y y +-+-+= 所以此弦所在直线方程是11(1),2y x -=--即230x y +-=．…………………12分 20. ⑴解：因为BC AB 2=，60ABC ︒∠=，在△ABC 中，由余弦定理可得 BC AC 3=，所以 BC AC ⊥．又因为 AC FB ⊥， 所以⊥AC 平面FBC ．因为⊥AC 平面FBC ，所以FC AC ⊥．因为FC CD ⊥，所以⊥FC 平面ABCD ,∴CF CB ⊥． …………………6分 (2)由(1)知,,CA CF CB 两两互相垂直，建立如图所示的空间直角坐标系xyz C -．在等腰梯形ABCD 中，可得 CB CD =．设1BC =，所以11(0,0,0),(0,1,0),,0),,1)22C A BDE --．所以 )1,21,23(-=，)0,0,3(=，)0,1,0(=． 设平面EAC 的法向量为=()x,y,z n ，则有0,0.CE CA ⎧⋅=⎪⎨⋅=⎪⎩n n 所以10,20.x y z -+== 取1z =，得=n (0,2,1)．设BC 与平面EAC 所成的角为θ，则||sin |cos ,|||||CB CB CB ⋅=〈〉==θn n n 所以 BC 与平面EAC 所成角的正弦值为552． (12)。

宜昌市部分示范高中教学协作体2019年春期中联考高二（理科）数学命题人：曹炼忠 审题人：梁环义 （全卷满分：150分 考试用时：120分钟）第Ⅰ卷（选择题 共60分）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题所给出的四个选项中，只有一项是符合题目要求的.1.命题“02000,sin 1x x R x x e ∃∈++<错误！未找到引用源。

”的否定是（ ）A ．02000,sin 1x x R x x e∃∈++>错误！未找到引用源。

B ．02000,sin 1x x R x x e∃∈++≥错误！未找到引用源。

C ．2,sin 1xx R x x e ∀∈++>错误！未找到引用源。

D ．2,sin 1xx R x x e ∀∈++≥错误！未找到引用源。

2.抛物线24x y =的准线方程为（ ） A. 1=xB. 1-=xC. 1=yD. 1-=y3.函数x x x f -=ln )(的单调递增区间是( ) A . )1,(-∞ B . ）（1,0C . ),0(+∞D .),1(+∞4.如图，已知正方体1111D C B A ABCD -，若 11z y x BD ++=，则x y z ++的值为（ ） A ．3 B ．1 C ．－1D ．－35.0>⋅n m 是方程1=-nm 表示双曲线的（ ） A.充分不必要条件 B.必要不充分条件 C. 充要条件D.既不充分也不必要条件6.1(2)0xe x dx +⎰ =（ ）A. 1B. 1-eC. eD. 1+e7.若双曲线)0(19222>=-a x a y 的一条渐近线与直线x y 31=垂直,则此双曲线的实轴长为( ) A . 2B . 4C . 18D . 368.函数y =x ex 3(其中e 为自然对数的底数)的大致图像是( )A B C D9.在三棱锥ABC S -中,,,SA AC AB AC AB ==⊥ABC SA 平面⊥,D 为BC 的中点,则异面直线AB 与SD 所成角的余弦值为( ) A.55 B.66 C.630 D.530 10.对于函数xxx f ln )(=,下列说法正确的有( ) ①)(x f 在e x =处取得极大值e1；②)(x f 有两个不同的零点；③)3()()4(f f f <<π.A.0个B.3个C.2个D.1个11.已知双曲线22:1(0,0)C a b a b-=>>的两条渐近线均与圆22650x y x +-+=相切，且双曲线的右焦点为该圆的圆心，则C 的离心率为（ ）A ．5B ．2C ．2 D ．312.已知函数⎩⎨⎧≤->=0,30,ln )(x kx x x x f 的图像上有两对关于y 轴对称的点，则实数k 的取值范围是（ ）A. ()0,2e - B. ⎪⎭⎫⎝⎛-0,212-e C. ()0,e - D.()0,22e -第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，共20分.请将正确答案填写在答题卡相应的位置上.13.曲线x x f sin )(=在点))0(,0(f 处的切线的倾斜角为 ． 14.已知()7,5,3A -，()3,3,1-B ，且2=，则C 点的坐标为 . 15.已知M 为抛物线28y x =上的一点，F 为抛物线的焦点，若120MFO ∠=︒，(2,0)N -（O 为坐标原点），则△MNF 的面积为 ．16.一边长为2的正方形纸板，在纸板的四角截去四个边长均为x 的小正方形，然后做成一个无盖方盒.方盒的容积的最大值为 .三、解答题：本大题共6小题，共70分.解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分10分)已知函数R x x x f ∈+-=，121)(2. （1）求函数)(x f 的图象在点（2，-1）处的切线方程；（2）求函数)(x f 的图象与直线1-=y 所围成的封闭图形的面积.18.（本小题满分12分）如图，在长方体1111D C B A ABCD -中，2,11===AB AD AA ，点E 是11D C 的中点．（1）求证：BCE DE 平面⊥； （2）求二面角C EB A --的大小．19.(本小题满分12分)已知椭圆的焦点在x 轴上，焦距为4，并且经过点），（2325-. （1）求该椭圆的标准方程；（2）该椭圆上是否存在一点，它到直线l :010=--y x 的距离最小？最小距离是多少？20.(本小题满分12分)如图，已知直三棱柱111C B A ABC - 中,,AC AB ⊥11,4,3AC C B AC AB ⊥==. （1）求1AA 的长；（2）若1=BP ，求直线1AA 与平面PC A 1所成角的余弦值．21.(本小题满分12分)已知直线l 与抛物线x y 22=交于B ，A (异于坐标原点O )两点. (1)若直线l 的方程为2-=x y ，求证:OB OA ⊥；(2)若OB OA ⊥,则直线l 是否恒过定点?若恒过定点，求出定点坐标；若不过定点，请说明理由.22.(本小题满分12分)设函数)0,,(21ln )(2≠∈++=c R c b bx x x c x f ，且1=x 为)(x f 的极值点．(1)若1=x 为)(x f 的极大值点，求)(x f 的单调区间(用c 表示)； (2)若0)(=x f 恰有两解，求实数c 的取值范围.宜昌市部分示范高中教学协作体2019年春期中联考高二（理科）数学参考答案一、选择题二、填空题 13．4π 14. )2,4,1(- 15. 38 16． 2716 三、解答题17．解：（1）由题意 x x f -=')( ...........1分 所求切线的斜率2)2(-='=f k ...........3分 所求切线方程为 )2(21--=+x y 即032=-+y x ..........5分（2）由⎪⎩⎪⎨⎧-=+-=11212y x y 解答 22=-=x x 或 (6)分所以所求的面积为[]31622)261(1)(2-23=-+-=+=⎰x x dx x f S . .........10分18．解：（1）建立如图所示的空间直角坐标系， 则D （0，0，0），E （0，1，1），B （1，2，0）， C （0，2，0），DE ＝（0，1，1），BE ＝（－1，－1，1），BC ＝（－1，0，0）．...............2分因为0,0DE BE DE BC ⋅=⋅=，所以,DE BE DE BC ⊥⊥． ...............4分则DE ⊥BE ，DE ⊥BC ． 因为BE ⊂平面BCE ，BC ⊂平面BCE ，BE ∩BC ＝B ， 所以DE ⊥平面BCE ．...............6分()()z y x n AEB ,,2=的法向量为设平面0000n AB y x y z n BE ⎧⋅==⎧⎪⎨⎨--+=⋅=⎩⎪⎩则即 ()1,0,1AEB n ∴=平面的一个法向量为.............8分(),0,1,1.DE BCE DE BCE ⊥∴=平面是平面的一个法向量1cos ,2n DE n DE n DE⋅<>==...............11分 .1200的大小为由图形可得二面角C EB A --...............12分19.解（1）由题意 设椭圆的方程为)0(12222>>=+b a by a x则⎪⎪⎩⎪⎪⎨⎧+==+-+++==2222210249)225(49)225(22c b a a c ..........3分6,10==∴b a ............4分161022=+yx 所求椭圆的标准方程为 .............5分2=+-n y x m 的方程为）设直线（⎪⎩⎪⎨⎧=+-=+161022n y x y x 由305108,22=-++n nx x y 得消去 ...........7分4,0±==∆n 解得由 . ............9分的距离最近，与椭圆的交点到时，直线由图像可知，当l m n 4-=间的距离与直线直线l m 232410=+-=d.23最小距离是∴ ...............12分20.解（1）以A 为坐标原点，建立如图所示的空间直角坐标系 设AA 1=t （t>0）,)0,0,3(),0,4,0(),,0,3(),,4,0(11B C t B t C),4,3(),,4,0(11t C B t AC --==.........2分11B C AC ⊥1120160AC B C t ∴⋅=∴-= .............4分.4,41的长为即AA t =∴ ...............5分(2)由（1）知)4,4,0(),3,0,3(04,0111-=-==A A ），（.....................6分),,(A 1z y x n PC =的法向量为设平面⎪⎩⎪⎨⎧=-==-=⋅∴04403311z y A n z x P A n)1,1,1(,1==x 得令 ....................8分33344,cos 1=>=< ....................10分.36AA 11所成角的余弦值为与平面直线PC A ∴ .................12分21.解:(1)证明:由⎩⎨⎧=-=xy x y 222得x 2-6x+4=0,解得x=3±5 ........2分不妨取A(3-5,1-5), B(3+5,1+5), ...........3分 ∴0=⋅, ∴OA ⊥OB. .............5分 (2)显然直线l 的斜率不为0,设直线l 的方程为x=ty+m(m ≠0),A(x 1,y 1),B(x 2,y 2), 由⎩⎨⎧=+=xy mty x 22消去x 得y 2-2ty-2m=0, ...................7分∴y 1y 2=-2m, x 1x 2=222221y y ⋅=m 2, ....................8分 由OA ⊥OB,得OB OA ⋅=x 1x 2+y 1y 2=m 2-2m=0,∴m=2, .............10分直线l 的方程为x=ty+2,∴直线l 恒过定点,且定点坐标为(2,0) ..............12分 22．解 f ′(x)＝c x ＋x ＋b ＝x 2＋bx ＋cx .因为f ′(1)＝0，所以b ＋c ＋1＝0，f ′(x)＝()()xc x x --1 且c ≠1 .........1分(1)因为x ＝1为f(x)的极大值点，所以c ＞1. .............2分 当0＜x ＜1时，f ′(x)＞0；当1＜x ＜c 时，f ′(x)＜0；当x ＞c 时，f ′(x)＞0. ..............4分 所以f(x)的单调递增区间为(0,1)，(c ，＋∞)；单调递减区间为(1，c)． ..... ........5分 (2)①若c ＜0，则f(x)在(0,1)上单调递减， 在(1，＋∞)上单调递增．若f(x)＝0恰有两解，则f(1)＜0，即12＋b ＜0.所以－12＜c ＜0. ..............7分 ②若0＜c ＜1，则f(x)极大值＝f(c)＝clnc ＋12c 2＋bc ，f(x)极小值＝f(1)＝12＋b.因为b ＝－1－c ，所以f(x)极大值＝clnc ＋c 22＋c(－1－c)＝clnc －c －c22＜0.f(x)极小值＝－12－c ＜0，从而f(x)＝0只有一解． .............9分③若c ＞1，则f(x)极小值＝clnc ＋c22＋c(－1－c)＝clnc －c －c 22＜0. f(x)极大值＝－12－c ＜0，则f(x)＝0只有一解． ..............11分 综上，使f(x)＝0恰有两解的c 的取值范围为(－12，0)． ...............12分。

2018年秋季湖北省普通高中联考协作体期中考试高二理科数学A 卷答案1—12题：DCDDA ABACB BD 13.12 14. 15.217.解：由⎩⎪⎨⎪⎧3x －y －10＝0，x ＋y －2＝0，得交点为(3，－1)． ………5’ 又直线AB 的斜率为-，所以直线l 的斜率为4，所以直线l 的方程为 4x —y —13＝0 ………10’18.解：设圆的方程为(x －a )2＋(y －b )2＝r 2， 由题意可得⎩⎪⎨⎪⎧a －3b ＝0，|a |＝r ，b 2＋8＝r 2，………9’ 解得⎩⎪⎨⎪⎧a ＝3，b ＝1，r ＝3或⎩⎪⎨⎪⎧a ＝－3，b ＝－1，r ＝3.所以圆的方程为(x －3)2＋(y －1)2＝9或(x ＋3)2＋(y ＋1)2＝9. ………12’19.(1)证明：因为PA ⊥AB ，PA ⊥BC ，所以PA ⊥平面ABC . 又因为BD ⊂平面ABC ，所以PA ⊥BD .又因为AB ＝BC ，D 为AC 的中点，所以BD ⊥AC .因为PA ∩AC=C,所以BD ⊥平面PAC ，所以平面BDE ⊥平面PAC . ………6’(2)解：因为PA ∥平面BDE ，平面PAC ∩平面BDE ＝DE ，所以PA ∥DE .因为D 为AC 的中点，所以DE ＝12PA ＝2， BD ＝DC ＝2 2.由(1)知，PA ⊥平面ABC ，所以DE ⊥平面ABC ，所以三棱锥E ­BCD 的体积V ＝16BD ·DC ·DE ＝ . ………12’ 20.(1)证明：因为四边形ABCD 是等腰梯形，AB ∥CD ，∠DAB ＝60°，所以∠ADC ＝∠BCD ＝120°.又因为CB ＝CD ，所以∠CDB ＝30°，所以∠ADB ＝90°，即AD ⊥BD .又AE ⊥BD ，且AE ∩AD ＝A ，所以BD ⊥平面AED . ………6’(2)解：取BD 的中点G ，连接CG ，FG ，由于CB ＝CD ，因此CG ⊥BD .因为FC ⊥平面ABCD ，BD ⊂平面ABCD ，所以FC ⊥BD .由于FC ∩CG ＝C ，FC ，CG ⊂平面FCG ，所以BD ⊥平面FCG ， 故BD ⊥FG ，所以∠FGC 为二面角F ­BD ­C 的平面角．在等腰三角形BCD 中，由于∠BCD ＝120°，因此CG ＝12CB . 又CB ＝CF ，所以GF ＝CG 2＋CF 2＝5CG ，故cos ∠FGC ＝55，因此二面角F­BD­C的余弦值为55.………12’21.解:(1)由题知,=11,=24,=, ∴= - ,∴y关于x的方程是x-.………8’(2)当x=10时,,误差是<1,当x=6时,,误差是<1,故该小组所得线性回归方程是理想的.………12’22.解:(1)由题意得10a+0.01×10+0.02×10+0.03×10+0.035×10=1,所以a =0.005.………3’(2)由直方图知,分数在[50,60]的频率为0.05,[60,70]的频率为0.35,[70,80]的频率为0.30,[80,90]的频率为0.20,[90,100]的频率为0.10,所以这100名学生期中考试数学成绩的平均分的估计值为55×0.05+65×0.35+75×0.30+85×0.20+95×0.10=74.5.………6’(3)由直方图得:第3组人数为0.3×100=30,第4组人数为0.2×100=20,第5组人数为0.1×100=10,所以利用分层抽样在60名学生中抽取6名学生时,每组分别抽取:第3组:×6=3(人),第4组:×6=2(人),第5组:×6=1(人).所以第3、4、5组分别抽取3人、2人、1人.设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的1位同学为C1,则从六位同学中抽两位同学有如下15种可能:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),其中恰有1人的分数不低于90的情形有:(A1,C1),(A2,C1),(A3,C1),(B1,C1),(B2,C1),共5种.故所求概率为. ………12’。

湖北省宜昌市第二中学2018-2019学年高二数学上学期期中试题 理本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分150分．考试时间120分钟．第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．复数5122iz i-=+的实部为（ ）A ．1-B ．0C ．1D ．24．当5,2m n ==时，执行图2所示的程序框图，输出的S 值为（ ）A ．20B ．42C ．60D ．1805．已知x R ∈，则“22x x =+”是“2x x =+”的（ ）A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件12．设函数322()32(0)f x x ax a x a =-+≠，若1212,()x x x x <是函数2()()g x f x a x λ=-的两个极值点，现给出如下结论：①若10λ-<<，则12()()f x f x <； ②若02λ<<，则12()()f x f x <；③若2λ>，则12()()f x f x <；期中正确的结论的个数为（ B ） A ．0B ．1C ．2D ．3第Ⅱ卷（非选择题 共90分）本卷包括必考题和选考题两部分，第13-22题为必考题，每个试题考生都必须作答． 二、填空题：本大共4小题，每小题5分，满分20分．14．已知0a >，()()412ax x -+的展开式中2x 的系数为1，则a 的值为 ．15．设袋子中装有3个红球，2个黄球，1个蓝球，规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分，现从该袋子中任取（有放回，且每球取得的机会均等）2个球，则取出此2球所得分数之和为3分的概率为 ．16．双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ，焦距为2c ，以右顶点A为圆心，半径为2a c+的圆与过1F 的直线l 相切于点N ．设l 与C 的交点为,P Q ，若PN PQ 2=，则双曲线C 的离心率为 ．三、解答题：本大题共7小题，共70分，解答须写出文字说明、证明过程或演算步骤．17．(本题满分10分)已知命题p ：2,1x R x m ∀∈+≥；命题q ：方程22122x y m m +=-+表示双曲线.(1) 若命题p 为真命题，求实数m 的取值范围；(2) 若命题“p q ∨”为真命题，“p q ∧”为假命题，求实数m 的取值范围． .18．(本题满分12分)19．(本题满分12分)为保障食品安全，某地食品监管部门对辖区某家食品企业进行检查，现从这家企业生产的某种同类产品中随机抽取了100件作为样本，并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下：质量指标值 [15,20) [20,25) [25,30) [30,35) [35,40) [40,45]等级次品 二等品 一等品 二等品 三等品 次品根据质量指标值的分组，统计得到了该企业的样本频率分布直方图（图表如下,其中0a >）.（Ⅰ）现从该企业生产的产品中任取一件，试估计该件产品为次品的概率；（Ⅱ）为守法经营、提高利润，该企业将所有次品销毁．．．．．．．，并将一等品的售价分别定为100元；二、三等品的售价定为50元.一名顾客随机购买了该企业销售的2件该食品，记其支付费用为X 元，用频率估计概率，求X 的分布列和数学期望； O质量指标值15 20 25 30 35 40 45 0.018.频率组距0.0800.03a21． (本题满分12分)22．(本题满分12分)已知椭圆1C ：22221x y a b+=()00a b >>，的焦点与抛物线2C ：2y =的焦点F 重合，且椭圆右顶点P 到F 的距离为3-. （Ⅰ）求椭圆1C 的方程；（Ⅱ）设直线l 与椭圆1C 交于A ，B 两点，且满足PA PB ⊥，求PAB ∆面积的最大值.数学（理科）参考答案一、选择题1-5: BBBCC 6-10:ABACC 11、A 12：B 二、填空题 13. 3 14.12 15. 1316.2 三、解答题17.解：⑴对于任意2,11x R x ∈+≥，若命题p 为真命题，则2min 1x m +≥（），所以1m ≤；……5分⑵若命题q 为真命题，则(2)(2)0m m -+<，所以22m -<<，……8分因为命题""p q ∨为真命题，则,p q 至少有一个真命题，""p q ∧为假命题， 则,p q 至少有一个假命题，所以,p q 一个为真命题，一个为假命题. ……10分 当命题p 为真命题，命题q 为假命题时，122m m m ≤⎧⎨≤-≥⎩或，则2m ≤-，当命题p 为假命题，命题q 为真命题时，122m m >⎧⎨-<<⎩，则12m <<，综上，212m m ≤-<<或. 18.解：1920.解：21.解：22. （Ⅰ）设椭圆1C 的半焦距为c ，依题意，可得a b >， 且(22,0),2,3223,1F c a c a b =-=-⇒== ，所以椭圆1C 的方程为2219x y += . （Ⅱ）依题意，可设直线,PA PB 的斜率存在且不为零， 不妨设直线:(3)PA y k x =-，则直线1:(3)PB y x k=--， 联立：22(3)19y k x x y =-⎧⎪⎨+=⎪⎩ 得2222(19)54(819)0k x k x k +-+-=， 则226119PA k k=++ 同理可得：22222166111919k PB k k k k =+=+++⋅， 所以PAB ∆的面积为：22222222222118(1)18(1)32(19)(9)9(1)64829(1)64k k k k S PA PB k k k k k k++===≤=+++++⋅， 当且仅当23(1)8k k +=，即47k ±=是面积取得最大值38.。

湖北省宜昌市2018-2019学年高二上学期期中考试数学（理）试题★祝考试顺利★注意事项：1、考试范围：高考范围。

2、答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。

3、选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4、填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

5、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

6、考试结束后，请将本试题卷、答题卡、草稿纸一并上交。

第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分，在每小题给的四个选项中，只有一个是符合题目要求的）1．设直线0ax by c ++=的倾斜角为α，且sin cos 0αα+=，则,a b 满足（ ）A.1=+b a B ．0=-b a C ．0=+b a D ．1=-b a 2．用“辗转相除法”求得459和357的最大公约数是（ ）A ．3B ．9C ．17D ．513．直线13kx y k -+=，当k 变动时，所有直线都通过定点（ ）A ．(0,0)B ．(3,1)C ．(0,1)D ．(2,1)4．圆22(2)5x y ++=关于原点(0,0)P 对称的圆的方程为 ( )A ．22(2)5x y -+=B ．22(2)5x y +-= C ．22(2)(2)5x y +++=D ．22(2)5x y ++=5．有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为( )A.5,10,15,20,25B.5,15,20,35,40C.10,20,30,40,50D.5,11,17,23,296．在一次歌手大奖赛上，七位评委为歌手打出的分数如下： 9.4 8.4 9.4 9.9 9.6 9.4 9.7去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( ) A ．9.4,0.484 B ．9.4,0.016 C ．9.5,0.016 D ．9.5,0.04 7．圆0422=-+x y x 在点)3,1(P 处的切线方程为（ ）A ．023=-+y xB ．043=-+y xC ．043=+-y xD ．023=+-y x 8． 2.5PM 是指悬浮在空气中的空气动力学当量直径小于或 等于2.5m μ的颗粒物,也称为细颗粒物,一般情况下 2.5PM 浓度(单位: 3·g m μ-)越大,大气环境质量越差.如图所示的是宜昌市区甲、乙两个监测站某10日内每日的 2.5PM 浓度读数的茎叶图,则下列说法正确的是( )A.这10日内甲、乙监测站读数的极差相等B.这10日内甲、乙监测站读数的中位数中,乙的较大C.这10日内乙监测站读数的众数与中位数相等D.这10日内甲、乙监测站读数的平均数相等9.点()4,2P -与圆224x y +=上任一点连结的线段的中点的轨迹方程( )A. ()()22211x y -++= B. ()()22214x y -++= C. ()()22424x y ++-= D. ()()22211x y ++-=10．两圆22440x y x y ++-=与222120x y x ++-=的公共弦长等于( )A. 4B. 11.若实数,x y 满足222210x y x y +--+=则42y x --的取值范围为( ) A. 40,3⎡⎤⎢⎥⎣⎦B. 4,3⎡⎫+∞⎪⎢⎣⎭C. 4,3⎛⎤-∞- ⎥⎝⎦D. 4,03⎡⎫-⎪⎢⎣⎭12．已知点(2,0)A -,(2,0)B ，(0,2)C ，直线(0)y ax b a =+>将ABC ∆分割为面积相等的两部分，则b 的取值范围是( )A.（0，2B. (2C. 2(2]3- D.2[,1)3二、填空题（本大题共4小题，每小题5分，共20分） 13. )5(412=__________)7(.14．已知圆M 与直线3x －4y ＝0及3x －4y ＋10＝0都相切，圆心在直线y ＝－x －4上，则圆M的方程为____________．15．阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为 .16.如图,已知直线334y x =-与x 轴、y 轴分别交于A ,B 两点, P 是以()0,1C 为圆心, 1为半径的圆上一动点,连接PA ,PB ,则PAB ∆面积的最大值是第Ⅱ卷三、解答题（解答应写出文字说明，证明过程，或演算步骤） 17．（本题满分10分）在锐角ABC ∆中，a ，b ，c 分别为角A ，B ，C 所对的边,2sin c A =． (Ⅰ) 确定角C 的大小;(Ⅱ) 若c =且ABC ∆的周长为5求ABC ∆的面积．18．（本题满分12分）某城市100户居民的月平均用电量(单位：度)，以[160，180)，[180，200)，[200，220)，[220，240)，[240，260)，[260，280)，[280，300)分组的频率分布直方图如图．(Ⅰ) 求直方图中x 的值；(Ⅱ)求月平均用电量的众数、中位数；(Ⅲ)在月平均用电量为[220，240)，[240，260)，[260，280)，[280，300)的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220，240)的用户中应抽取多少户？19．（本题满分12分）如图，AB 是圆的直径，PA 垂直圆所在的平面，C 是圆上的点. （Ⅰ）求证：平面PAC ⊥平面PBC ；（Ⅱ）若AB =2，AC =1，PA =1，求二面角C -PB -A 的余弦值. 20．（本题满分12分）以下是某地搜集到的新房屋的销售价格y 和房屋的面积x 的数据：(Ⅰ) 画出数据对应的散点图；(Ⅱ) 求线性回归方程，并在散点图中加上回归直线； (Ⅲ)据(Ⅱ)的结果估计当房屋面积为2150m 时的销售价格.附：对于一组数据()11,u v ， ()22,u v ，…(),n n u v ，其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为()()121()ˆniii nii u u v v u u β==--=-∑∑， ˆˆˆv u αβ=- 21．（本题满分12分）如图,在平面直角坐标系 xOy 中,已知圆22:40C x y x +-=及点(1,0),(1,2)A B - (Ⅰ)若直线l 平行于AB ,与圆 C 相交于,M N 两点,MN AB =,求直线l 的方程;(Ⅱ)在圆 C 上是否存在点P ,使得2212?PA PB +=若存在,求点P 的个数;若不存在,说明理由. 22．（本题满分12分）已知各项均为正数的数列{}n a ,满足()221120*n n n n a a a a n N ++--=∈ 且12a =.(Ⅰ)求数列{}n a 的通项公式； (Ⅱ)设12log n n n b a a =⋅,若n b 的前n 项和为n S ,求nS ；(Ⅲ)在（2）的条件下,求使1250n n S n ++⋅>成立的正整数n 的最小值．数学试题（理科） 答案1—12. BDBAC CDCAD AB13. 212 14. ()x ＋32＋()y ＋12＝1 15. 9 16. 21217．解：（12sin c A =2sin sin A C A =，因为sin 0A ≠，所以sin 2C =. 所以3C π=或23C π=. 因为ABC ∆是锐角三角形， 所以3C π=.（2）因为c =ABC ∆的周长为5a +b =5 ①由余弦定理得222cos73a b ab π+-= ，即227a b ab +-= ②由②变形得()237a b ab +-=，所以ab =6，得1sin 23S ab π==18. 解：(Ⅰ)由直方图的性质可得(0.002＋0.009 5＋0.011＋0.012 5＋x ＋0.005＋0.002 5)×20＝1，解方程可得x ＝0.007 5.∴直方图中x 的值为0.007 5；(2分) (Ⅱ)月平均用电量的众数是220＋2402＝230，------(4分) ∵(0.002＋0.009 5＋0.011)×20＝0.45<0.5， ∴月平均用电量的中位数在[220，240)内，设中位数为a ，由(0.002＋0.009 5＋0.011)×20＋0.012 5×(a－220)＝0.5可得a ＝224. ∴月平均用电量的中位数为224；--------(6分)(Ⅲ)月平均用电量为[220，240)的用户有0.012 5×20×100＝25， 月平均用电量为[240，260)的用户有0.007 5×20×100＝15， 月平均用电量为[260，280)的用户有0.005×20×100＝10， 月平均用电量为[280，300)的用户有0.002 5×20×100＝5， ∴抽取比例为1125＋15＋10＋5＝15，--------(11分)∴月平均用电量在[220，240)的用户中应抽取25×15＝5（户）．-------（12分）19. 证明：（Ⅰ）由AB 是圆的直径，得AC BC ⊥， 由PA ⊥平面ABC ，BC ⊂平面ABC ，得PA BC ⊥． 又PA AC A ⋂=，PA ⊂平面PAC ，AC ⊂平面PAC ， 所以BC ⊥平面PAC ． 因为BC ⊂平面PBC ，所以平面PAC ⊥平面PBC ……………………………………………6分 （Ⅱ）解法一：过C 作CM//AP ，则CM ⊥平面ABC ．如图（1），以点C 为坐标原点，分别 以直线CB ，CA ，CM 为x 轴，y 轴，z 轴建立空间直角坐标系．在Rt △ABC 中，因为AB =2，AC =1，所以BC =又因为PA =1，所以A （0，1， 0），B0，0），P （0，1，1）．故(3,0,0),(0,1,1)CB CP ==． 设平面BCP 的法向量为1111(,,)x y z =n ，则110,0.⎧=⎪⎨=⎪⎩CB n CP n 所以1110,0.y z =+=⎪⎩不妨令11y =，则1(0,1,1)=-n ． 因为(0,0,1),(3,1,0),AP AB ==- 设平面ABP 的法向量为2222(,,)x y z =n ，则220,0.AP ⎧=⎪⎨=⎪⎩n AB n 所以2220,0.z y =⎧⎪-=不妨令21x =，则20)=n ．于是12cos ,〈〉=n n 由图（1）知二面角C -PB -A 为锐角，第18题图（1）故二面角C -PB -A的余弦值为…………………………12分 （Ⅱ）解法二：如图（2），过C 作CM ⊥AB 于M ， 因为PA ⊥平面ABC ，CM ⊂平面ABC ， 所以PA ⊥CM ．又因为PA AB A ⋂=，且PA ⊂平面PAB ，AB ⊂平面PAB ， 所以CM ⊥平面PAB ．过M 作MN ⊥PB 于N ，连接NC ， 由三垂线定理得CN ⊥PB ，所以∠CNM 为二面角C -PB -A 的平面角． 在Rt △ABC 中，由AB =2，AC =1，得BCCM =，32BM =． 在Rt △PAB 中，由AB =2，PA =1，得PB 因为Rt △BNM ∽Rt△BAP ，所以31MNMN =所以在Rt △CNM中，CN =，所以cos CNM ∠=， 所以故二面角C -PB -A的余弦值为…………………………12分20.（1）数据对应的散点图如图所示：（2）1095151==∑=i i x x ，1570)(251=-=∑=x x l i i xx ，第18题图（2）308))((,2.2351=--==∑=y y x x l y i i i xy设所求回归直线方程为a bx y +=，则1962.01570308≈==xxxy l l b ， 8166.115703081092.23≈⨯-=-=x b y a 故所求回归直线方程为8166.11962.0+=x y（3）据（2），当2150x m =时，销售价格的估计值为：2466.318166.11501962.0=+⨯=y（万元）21. 解析：1.圆C 的标准方程为22(2)4x y -+=, 所以圆心(2,0)C ,半径为2.因为//,(1,0),(1,2)l AB A B -,所以直线l 的斜率为2011(1)-=--,设直线l 的方程为0x y m -+=,则圆心 C 到直线l 的距离为d ==因为MN AB ===而2222MN CM d ⎛⎫=+ ⎪⎝⎭,所以2(2)422m +=+, 解得0m =或4-,故直l 线的方程为0x y -=或40x y --=. 2.假设圆 C 上存在点P ,设(,)P x y ,则22(2)4x y -+=,222222(1)(0)(1)(2)12PA PB x y x y +=++-+-+-=,即22230x y y +--=,即22(1)4x y +-=,因为2222-<+所以圆22(2)4x y -+=22(1)4x y +-=与圆相交, 所以点P 的个数为222．解：（1）∵221120n n n n a a a a ++--=，()()1120n n n n a a a a ++∴+-=∵数列{}n a 的各项均为正数，∴10n n a a ++>， ∴120n n a a +-=，即()12*n n a a n N +=∈ 所以数列{}n a 是以2为公比的等比数列. ∵12a =，∴数列{}n a 的通项公式2nn a =.（2）由（1）及12log n n n b a a =得，2n nb n =-⋅，∵12n n S b b b =+++，∴23422232422n n S n =--⋅-⋅-⋅--⋅①∴()2345122223242122n n n S n n +=--⋅-⋅-⋅---⋅-⋅②②-①得()()23451112122222222212212n n n n n n S n n n +++-=++++++-⋅=-⋅=-⋅--（3）要使1250n n S n ++⋅>成立，只需12250n +->成立，即1252n +>，∴使1250n n S n ++⋅>成立的正整数n 的最小值为5.附：双向细目表。

宜昌市部分示范高中教学协作体2019年秋期中联考高二数学（全卷满分：150分 考试用时：150分钟）一、选择题:本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1、已知两点()()1,2,3,4A B -，则直线AB 的斜率为A. 2B. 21-C.21D. 2-2、数列3，5，9，17，33，…的一个通项公式n a 可以为( )A. 21n +B. 12+nC.12-nD. 121n +-3、在等比数列{}n a 中，12,34321=+=+a a a a ，则65a a +的值为 ( )A. 18B. 21C. 24D. 484、过点()3,1-P 且倾斜角为 30的直线方程为（ ）A. 03433=+-y xB. 0323=+-y xC. 03233=+-y xD. 03=-y x5、已知数列{}n a 的前n 项和n n S n -=2，则=5a ( )A. 6B. 8C. 12D. 206、已知圆过()()()1,2,1,0,3,0A B C --三点，则圆的方程是（ ）A. 09422=--+x y x B. 05422=-++x y x C. 07222=--+x y x D. 03222=-++x y x7、在等差数列{}n a 中，若76,a a 是方程0132=-+x x 的两根，则{}n a 的前12项的和为( )A. 6B. 18C. -18D. -68、不论m 为何实数，直线()0121=+---m y x m 恒过定点（ ）A.()1,1-B.()1,2-C.()1,2--D. ()1,19、已知数列{}n a 满足3,211-==-+a a a n n ，则=+++521a a a ( )A. 13B. 8C. 5D. 2010、已知数列{}n a 满足nn n a a a 2,211+==+，则n a =（ ）A.2nB. n 2C. 121+-nD.221-+n11、已知()()0,1,4,2B A ，动点P 在直线1-=x 上，当PB PA +取最小值时，则点P 的坐标为（ ）A.⎪⎭⎫ ⎝⎛-58,1 B. ⎪⎭⎫ ⎝⎛-521,1 C. ()2,1- D. ()1,1-12、直线01=-+ay ax 与圆0122222=+-+a y a x a 有公共点()00,y x ，则00y x 的最大值为（ ）A.41- B.34C.94D. 2二、填空题：本大题共4小题，每小题5分，共20分. 13、已知直线013:=-+y x l ，则直线l 的倾斜角为______．14、已知点()()()2,3,2,1,,2A B C x --，若A 、B 、C 三点共线，则x 的值为______．15、已知1，a,b,c,4成等比数列，则b=______．16、已知圆012:22=--+x y x C ，以点1,12⎛⎫⎪⎝⎭为中点的弦所在的直线方程是______．三、解答题：解答题应写出文字说明，证明过程或演算步骤. 17、（本小题满分10分） 已知直线l 过点()2,3P ．⑴若直线l 与052=++y x 平行，求直线l 的方程; ⑵若直线l 在两坐标轴上的截距相等，求直线l 的方程．18、（本小题满分12分）在等差数列{}n a 中，13,5543=+=a a a （1）求数列{}n a 的通项公式； （2）设n b n a n +=-22，求数列{}n b 的前n 项和n S ．19、（本小题满分12分）已知递增等比数列{}n a 满足：13,332==S a⑴求{}n a 的通项公式及前n 项和n S ； ⑵设()13log 11+⋅+=n n a n b ，求数列{}n b 的前n 项和n T．20、（本小题满分12分）已知曲线方程042:22=+--+m y x y x C .⑴ 若曲线C 表示圆，求m 的取值范围；⑵ 当m=4时，求圆心和半径；⑶当m=4时，若圆C 与直线04:=-+y x l 相交于M 、N 两点，求线段 MN 的长．21、（本小题满分12分）已知数列{}n a 的前n 项和为n S ，且满足n a S n n 323-=.（1）求数列{}n a 的前三项123,,a a a ； （2）证明数列{}1+n a 为等比数列； （3）求数列⎭⎬⎫⎩⎨⎧+1n a n 的前n 项和n T ．22、（本小题满分12分）在平面直角坐标系xoy 中，直线0123=+++y x 与圆C 相切，圆心C 的坐标为()1,2-．（1）求圆C 的方程；（2）设直线1+=kx y 与圆C 没有公共点，求k 的取值范围;（3）设直线m x y +=与圆C 交于M 、N 两点，且OM ⊥ON ，求m 的值．（2）宜昌市部分示范高中教学协作体2019年秋期中联考高二数学参考答案一、选择题（本大题共12小题，共60.0分）二、填空题（本大题共4小题，共20.0分） 13、65π14、-1 15、 2 16、2x-4y+3=0三、解答题（本大题共6小题，共70.0分） 17、解：（1）设直线方程为1y=-2x m +，因为过点()2,3P ， 所以13242m m =-⨯+⇒=，从而直线方程为142y x =-+，即280x y +-=为所求；'4（2）①当直线经过原点时，可得直线方程为：32y x =，即320x y -=． '7②当直线不经过原点时，可设直线方程为1x ya a+=， 把点()2,3代入可得：2315a a a+=⇒=，可得直线方程为50x y +-=． 综上所述：所求的直线方程为：320x y -=或50x y +-=． '1018、解：（1）设等差数列{a n }的公差为d ，由题意得111253413a d a d a d +=⎧⎨+++=⎩，解得131a d =⎧⎨=⎩,'3∴a n =3+（n -1）×1，即a n =n +2． '5（2）2n a n =+222n a n n b n n-∴=+=+'7所以()()()()231232122232n n n S b b b b n =++++=++++++++()()23222212+3++n n =++++++'9()211222421222n n n n n n ++-⨯+-=+=+- '1219、解：（1）由题可知()舍或⎪⎩⎪⎨⎧==⎩⎨⎧==⇒⎩⎨⎧==319311331132q a q a S a '2 所以{}n a 的通项公式13-=n n a '4前n 项和()213111-=--=n n n q q a S ； '6（2）由（1）知nn a 31=+所以()()11111log 1113+-=+=⋅+=+n n n n a n b n n '9所以数列{}n b 的前n 项和⎪⎭⎫ ⎝⎛+-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=++++=11141313121211321n n b b b b T n n 1111nn n =-=++.故数列{}n b 的前n 项和1n n T n =+. '1220、解：由22240x y x y m +--+=得()()22125x y m -+-=-（1）若曲线C 表示圆，则50m ->,所以5m <. '3 （2）当m=4，则圆为()()22121x y -+-=此时，该圆的圆心为()1,2，半径为1； '6（3）当m=4,则圆的方程为()()22121x y -+-=， 圆心()1,2到直线40x y +-=的距离2d ==因为圆的半径为1，所以22MN === 故线段MN. '1221、解：（1）由题意得1113233S a a =-⇒=-，22232323S a a =-⨯⇒=， 33332339S a a =-⨯⇒=-所以数列{}n a 的前三项1233,3,9a a a =-==-；'3（2）因为323n n S a n =-，所以()1233n n S a n =- ……① 当2n ≥时，()1112333n n S a n --=-+②①-②，得122133n n n a a a -=--1112321n n n n a a a a --+⇒=--⇒=-+ 112a +=- {}1n a ∴+是以-2为首项，-2为公比的等比数列()()1221n nn n a a ∴+=-⇒=--'7（3）设1n n nb a =+，则()2n n n b =-所以n 123T n b b b b =++++，()()()()1231232222n nnT \=++++----，12n T \-=()()()()2311212222nn n n+-++++----'9两式相减得()()()()()23131111222222n nn nT +=++++------，()()11112221212nn n +⎛⎫--⋅- ⎪⎝⎭-=-⎛⎫--- ⎪⎝⎭()1321332n n ++=--- ()1642992n n n T ++⇒=--⋅-即为所求'1222、解：（Ⅰ）设圆的方程是（x -1）2+（y +2）2=r 2，依题意∵C （1，-2）为圆心的圆与直线10x y ++=相切．∴所求圆的半径，3r ==，∴所求的圆方程是（x -1）2+（y +2）2=9． '3 （Ⅱ）圆心C （1，-2）到直线y =kx +1的距离d ==，∵y =kx +1与圆没有公共点，∴d ＞r3>，解得0＜k ＜34． k 的取值范围：（0，34）． '6（Ⅲ）设M （x 1，y 1），N （x 2，y 2）， 联立方程组()()22129y x m x y =+⎧⎪⎨-++=⎪⎩， 消去y ，得到方程2x 2+2（m +1）x +m 2+4m -4=0，∴ x 1+x 2=-m -1，x 1x 2=2442m m +- , ①'8由已知可得，判别式∆=4（m +1）2-4×2（m 2+4m -4）＞0，化简得m 2+6m -9＜0， 由于OM ⊥ON ，可得x 1x 2+y 1y 2=0, '10又y 1=-x 1-m ，y 2=-x 2-m , 所以2x 1x 2+m （x 1+x 2）+m 2=0， ②由①，②得m =-4或m =1，满足∆＞0， 故m =1或m =-4． '12。