下载文档原格式
傅里叶分析之掐死教程（完整版）更新于2014.06.06Heinrich · 6 个月前作者：韩昊知乎：Heinrich 微博：@花生油工人知乎专栏：与时间无关的故事谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。
转载的同学请保留上面这句话，谢谢。
如果还能保留文章来源就更感激不尽了。
我保证这篇文章和你以前看过的所有文章都不同，这是12年还在果壳的时候写的，但是当时没有来得及写完就出国了……于是拖了两年，嗯，我是拖延症患者……这篇文章的核心思想就是：要让读者在不看任何数学公式的情况下理解傅里叶分析。
傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。
但不幸的是，傅里叶分析的公式看起来太复杂了，所以很多大一新生上来就懵圈并从此对它深恶痛绝。
老实说，这么有意思的东西居然成了大学里的杀手课程，不得不归咎于编教材的人实在是太严肃了。
（您把教材写得好玩一点会死吗？会死吗？）所以我一直想写一个有意思的文章来解释傅里叶分析，有可能的话高中生都能看懂的那种。
所以，不管读到这里的您从事何种工作，我保证您都能看懂，并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。
至于对于已经有一定基础的朋友，也希望不要看到会的地方就急忙往后翻，仔细读一定会有新的发现。
——————————————以上是定场诗——————————————下面进入正题：抱歉，还是要啰嗦一句：其实学习本来就不是易事，我写这篇文章的初衷也是希望大家学习起来更加轻松，充满乐趣。
但是千万！千万不要把这篇文章收藏起来，或是存下地址，心里想着：以后有时间再看。
这样的例子太多了，也许几年后你都没有再打开这个页面。
无论如何，耐下心，读下去。
这篇文章要比读课本要轻松、开心得多……p.s.本文无论是cos还是sin，都统一用“正弦波”（Sine Wave）一词来代表简谐波。
一、什么是频域从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。
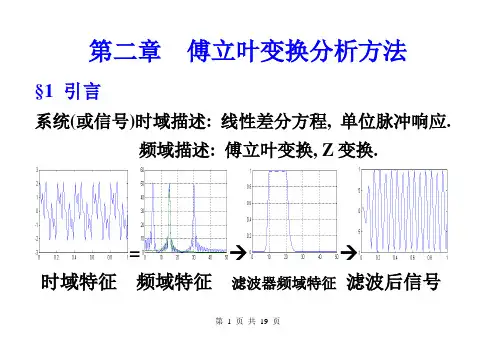
第二章傅立叶变换分析方法§1 引言系统(或信号)时域描述: 线性差分方程, 单位脉冲响应.频域描述: 傅立叶变换, Z变换.=→→时域特征频域特征滤波器频域特征滤波后信号§2 序列的傅立叶变换1. 定义: j jn n X e x n e()()ωω∞-=-∞∑;()j X eω称为()x n 的傅立叶变换, 也称频谱函数.简记 ()j X e ω=FT[x (n )]; 注意1当ω定时,jn eω-是n 的序列,≈≈≈∑内积投影分量注意2 结果()j X e ω是ω的连续函数. 2. x n {()}的FT 存在 n x n |()|∞=-∞⇔<∞∑;3. 傅立叶反变换:-=⎰j jn x n X ee1()()d 2πωωπωπ.简记 x (n )=IFT[()j X e ω]. 4. j X e ()ω的幅频, 相频表示:arg[()]()()j j j j X eX eX eeωωω=例1 求()n δ的FT.解 ()()1j jn n X e n eωωδ∞-=-∞==∑,ω)例2 求4()()x n R n =的傅立叶变换. 解 对任给一个[0,2]ωπ∈, 有1()()N j jn jn N n n X eR n eeωωω∞---=-∞===∑∑/2/2/2/2/2/21()1()j N j N j N j N j j j j eeeeeee eωωωωωωωω--------==--(1)/2sin(/2)sin(/2)j N N eωωω--=当N =4时, 有3/2sin(2)()sin(/2)j j X e eωωωω-=当0,,,42ππωπ=时的()j X eω各点, 见右图.其值意义为:原序列在各数字频率上的分量.由于当=ωπ时, 序列=cos jn en ωωππ-=变化最剧烈,即数字频率最高值为π.cos(npi)图: n=[-3 -2 -1 0 1 2 3 4]; stem(n,cos(n*pi));ππ-π-2ππ2πX(e jw)的程序计算说明: 对每个w 有11(1)()()[(0),(1),...,(1)]...jw jw N jw jw n n jw N e e X e x n e x x x N e -⋅-⋅--=-⋅-⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎣⎦∑对各个000,2,...,w w K w 有:0002(),(),...,()jw j w jK w X e X e X e ⎡⎤⎣⎦00000000010200112111(1)2(1)(1)[(0),(1),...,(1)],,...,.........jw jw jw K jw jw jw K jw N jw N jw K N e e e e e e x x x N e e e -⋅⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅--⋅⋅--⋅⋅-⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦1020011211,,...,.........1(1)2(1)(1)[(0),(1),...,(1)]()K K N N K N jw x x x N e⋅⋅⋅⎡⎤⎢⎥⋅⋅⋅⎢⎥⎢⎥⎢⎥⋅-⋅-⋅--⎣⎦=-[]011,2,...,...1[(0),(1),...,(1)]()K N jw x x x N e⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦=-%X(e jw)的作图xn=[1 1 1 1]; n=0:3;k=0:100; w=pi/50*k;xw=xn*(exp(-j*pi/50)).^(n'*k); magx=abs(xw);magx2=[magx,magx]; w2=[w-2*pi,w,]; %拼成2pi angx=angle(xw); angx2=[angx,angx];%X(e jw)的幅频图subplot(2,1,1);plot(w2,magx2);%X(e jw)的相频图subplot(2,1,2);plot(w2,angx2);%也可直接作出Xw=0:2*pi/100:2*pi;plot(w,abs(sin(2*w)./sin(w/2))); Warning: Divide by zero.ππ-π-2ππ2π§3 序列的傅立叶变换性质 1. 周期性 (关于w)(2)(2)()()()j M j M nj n X ex n eX eωπωπω∞+-+=-∞==∑2. 线性性设11()FT[()]j X e x n ω=, 22()FT[()]j X e x n ω=, 则1212FT[()()]()()j j ax n bx n aX e bX e ωω+=+.(,a b ∀). 证 按定义即得.3. 时移,频移 设()F T [()]j X e x n ω=, 则0FT[()]()j n j x n n e X eωω--=;00()FT[()]()j nj ex n X eωωω-=.证 由定义得(i) 00F T [()]()j nn x n n x n n eω∞-=-∞-=-∑()()j m j n j n j m m n n x m eeX eωωωω∞---=-∞=-=∑.(ii) 00F T [()]()j nj nj nn ex n ex n eωωω∞-=-∞=∑00()()()()j nj n x n eX eωωωω∞---=-∞==∑.例1 求40()R n n -的FT. 解 00()F T [()]F T [()]j n j N N Y eR n n e R n ωω-=-= 0()j n j eX eωω-=.4. 共轭对称(1) 时域上对称(关于n)(0) 称()x n 是对称序列: 若()();x n x n -= (i) 称()x n 是共轭对称序列: 若()*();x n x n -=(ii) 称()x n 是共轭反对称序列: 若()*();x n x n -=- (2) 频域上对称(关于w)(i')称()j X e ω是共轭对称函数: 若()()j j X eX eωω-*=;(ii')称()j X e ω是共轭反对称函数若()()j j X e X eωω-*=-;例2 分析()j nx n e ω=的对称性.解 因()()j nx n ex n ω-*-==, 故()x n 共轭对称.<1>共轭对称序列的虚实分解: 实部偶+j 虚部奇; ()()(),()()()r i r i x n x n jx n x n x n jx n =+-=-+- 由()*()x n x n -=,得()(),()()r r i i x n x n x n x n -=-=-.<2>共轭反对称序列的虚实分解: 实部奇+j 虚部偶 例3 分析()j ny n je ω=对称性.解 ()()()()j nj nj ny n jeje jey n ωωω-***-==-=-=-==> 共轭反对称, 实部奇, 虚部偶.(3) 实()x n 的FT 为共轭对称(主要) 设()=()j jn n X e x n eωω∞-=-∞∑, 则()=()()()j jn jn j n n X ex n ex n eX e ωωωω*∞∞--*=-∞=-∞⎛⎫== ⎪⎝⎭∑∑(易得, 对纯()jx n 的FT 为共轭反对称) (4) 复序列的FT 性质(介绍) 设 ()()(),r i x n x n jx n =+ 作FT 得()FT[()]FT[()]FT[()]j r i X ex n x n jx n ω==+ ()().j j e o X eX eωω+(),().j j e o X eX eωω其中共轭对称共轭反对称时域中虚实分解==>频域中共轭对称与反对称分解 5. 时域卷积 (=>频域乘积)前有 ()()()()()m y n x n h n x m h n m ∞=-∞=*=-∑, 现有()F T[()]()()j j nn m Y ey n x m h n m eωω∞∞-=-∞=-∞==-∑∑令k n m =-，得()()()j j mj kk m Y ex m eh k eωωω∞∞--=-∞=-∞=∑∑()()j j H eX eωω=6. (时域乘积=>)频域卷积设()()()y n x n h n =, 则有()F T[()]()()j j nn Y ey n x n h n eωω∞-=-∞==∑∞--=-∞⎛⎫=⎪⎝⎭∑⎰j j nj n n x n H eee 1()()d 2πθθωπθπ∞--=-∞=∑⎰j j nj nn H e x n ee1()()d 2πθωθπθπ∞---=-∞=∑⎰j j nn H ex n e()1()()d 2πθωθπθπ--==*⎰j j j j H e X eH eX e()11()()d ()()22πθωθωωπθππ即 1()()()2j j j Y e H eX eωωωπ=*.7. 帕斯维尔(Parseval)(时频能量守恒)221()()d 2j n x n X eπωπωπ∞-=-∞=∑⎰.证 设2()()()()y n x n x n x n *== 及()()()()j nj n j j n n x n ex n e X e X e ωωωω*∞∞**--*-=-∞=-∞⎛⎫⎡⎤=== ⎪⎣⎦⎝⎭∑∑, 则有()F T [()]F T[()()]j Y ey n x n x n ω*==()()j nn x n x n eω∞*-=-∞=∑j j X eX e1()()2ωωπ*-=**---=⎰j j X eX e()1()()d 2πθωθπθπ.令=0ω,得n n x n x n x n 2()()()∞∞*=-∞=-∞=∑∑*-=⎰j j X eX e1()()d 2πθθπθπ21=()d 2j X eπθπθπ-⎰.部分性质汇总在表2.3.1中, P39. 作业P481;3; 4(1,3,5); 5; 8(1,3); 9(2).。
FFT是离散傅里叶变换的快速算法，可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。
FFT结果的具体物理意义。
一个模拟信号，经过ADC采样之后，就变成了数字信号。
采样定理告诉我们，采样频率要大于信号频率的两倍。
采样得到的数字信号，就可以做FFT变换了。
N个采样点，经过FFT之后，就可以得到N个点的FFT结果。
为了方便进行FFT运算，通常N取2的整数次方。
假设采样频率为Fs，信号频率F，采样点数为N。
那么FFT之后结果就是一个为N点的复数。
每一个点就对应着一个频率点。
这个点的模值，就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。
而第一个点就是直流分量，它的模值就是直流分量的N倍。
而每个点的相位呢，就是在该频率下的信号的相位。
第一个点表示直流分量（即0Hz），而最后一个点N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被N-1个点平均分成N等份，每个点的频率依次增加。
例如某点n所表示的频率为：Fn=(n-1)*Fs/N。
由上面的公式可以看出，Fn所能分辨到频率为为Fs/N，如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。
1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。
如果要提高频率分辨力，则必须增加采样点数，也即采样时间。
频率分辨率和采样时间是倒数关系。
假设FFT之后某点n用复数a+bi表示，那么这个复数的模就是An=根号a*a+b*b，相位就是Pn=atan2(b,a)。
关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解,最近,我偶尔从网上看到一个关于数字信号处理的电子书籍,是一个叫Steven W. Smith, Ph.D.外国人写的,写得非常浅显,里面有七章由浅入深地专门讲述关于离散信号的傅立叶变换,虽然是英文文档,我还是硬着头皮看完了有关傅立叶变换的有关内容,看了有茅塞顿开的感觉,在此把我从中得到的理解拿出来跟大家分享,希望很多被傅立叶变换迷惑的朋友能够得到一点启发,这电子书籍是免费的,有兴趣的朋友也可以从网上下载下来看一下,URL地址是：要理解傅立叶变换,确实需要一定的耐心,别一下子想着傅立叶变换是怎么变换的,当然,也需要一定的高等数学基础,最基本的是级数变换,其中傅立叶级数变换是傅立叶变换的基础公式。
二、傅立叶变换的提出让我们先看看为什么会有傅立叶变换？傅立叶是一位法国数学家和物理学家的名字,英语原名是Jean Baptiste Joseph Fourier<1768-1830>, Fourier对热传递很感兴趣,于1807年在法国科学学会上发表了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断：任何连续周期信号可以由一组适当的正弦曲线组合而成。
当时审查这个论文的人,其中有两位是历史上著名的数学家拉格朗日<Joseph Louis Lagrange, 1736-1813>和拉普拉斯<Pierre Simon de Laplace, 1749-1827>,当拉普拉斯和其它审查者投票通过并要发表这个论文时,拉格朗日坚决反对,在近50年的时间里,拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。
法国科学学会屈服于拉格朗日的威望,拒绝了傅立叶的工作,幸运的是,傅立叶还有其它事情可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后因会被推上断头台而一直在逃避。
第一章 信号与系统的基本概念1．信号、信息与消息的差别？信号：随时间变化的物理量；消息：待传送的一种以收发双方事先约定的方式组成的符号，如语言、文字、图像、数据等信息：所接收到的未知内容的消息，即传输的信号是带有信息的。
2．什么是奇异信号？函数本身有不连续点或其导数或积分有不连续点的这类函数统称为奇异信号或奇异函数。
例如：单边指数信号 （在t =0点时，不连续），单边正弦信号 （在t =0时的一阶导函数不连续）。
较为重要的两种奇异信号是单位冲激信号δ(t )和单位阶跃信号u(t )。
3．单位冲激信号的物理意义及其取样性质？冲激信号：它是一种奇异函数，可以由一些常规函数的广义极限而得到。
它表达的是一类幅度很强，但作用时间很短的物理现象。
其重要特性是筛选性，即：()()()(0)(0)t x t dt t x dt x δδ∞∞-∞-∞==⎰⎰ 4．什么是单位阶跃信号？单位阶跃信号也是一类奇异信号，定义为：10()00t u t t >⎧=⎨<⎩它可以表示单边信号，持续时间有限信号，在信号处理中起着重要的作用。
5．线性时不变系统的意义同时满足叠加性和均匀性以及时不变特性的系统，称为线性时不变系统。
即：如果一个系统，当输入信号分别为1()x t 和2()x t 时，输出信号分别是1()y t 和2()y t 。
当输入信号()x t 是1()x t 和2()x t 的线性叠加，即：12()()()x t ax t bx t =+，其中a 和b 是任意常数时，输出信号()y t 是1()y t 和2()y t 的线性叠加，即：12()()()y t ay t by t =+；且当输入信号()x t 出现延时，即输入信号是0()x t t -时， 输出信号也产生同样的延时，即输出信号是0()y t t -。
其中，如果当12()()()x t x t x t =+时，12()()()y t y t y t =+，则称系统具有叠加性；如果当1()()x t ax t =时，1()()y t ay t =则称系统具有均匀性。
线性时不变系统是最基本的一类系统，是研究复杂系统，如非线性、时变系统的基础。
6．线性时不变系统的意义与应用？线性时不变系统是我们本课程分析和研究的主要对象，对线性时不变性进行推广，可以得到线性时不变系统具有微分与积分性质，假设系统的输入与输出信号分别为()x t 和()y t ，则 当输入信号为()dx t dt 时，输出信号则为()dy t dt； 或者当输入信号为()t x d ττ-∞⎰时，输出信号则为()ty d ττ-∞⎰。
另外，线性时不变系统对信号的处理作用可以用冲激响应（或单位脉冲响应）、系统函数或频率响应进行描述。
而且多个系统可以以不同的方式进行连接，基本的连接方式为：级联和并联。
假设两个线性时不变系统的冲激响应分别为：1()h t 和2()h t ，当两个系统级联后，整个系统的冲激响应为：12()()*()h t h t h t =；当两个系统并联后，整个系统的冲激响应为：12()()()h t h t h t =+；当0t <时，若()0h t =， 则此系统为因果系统；若|()|h t dt ∞-∞<∞⎰， 则此系统为稳定系统。
第二章 连续时间系统的时域分析1．如何获得系统的数学模型？数学模型是实际系统分析的一种重要手段，广泛应用于各种类型系统的分析和控制之中。
不同的系统，其数学模型可能具有不同的形式和特点。
对于线性时不变系统，其数学模型通常由两种形式：建立输入-输出信号之间关系的一个方程或建立系统状态转换的若干个方程组成的方程组（状态方程）。
对于本课程研究较多的电类系统而言，建立系统数学模型主要依据两个约束特性：元件特性约束和网络拓扑约束。
一般地，对于线性时不变连续时间系统，其输入-输出方程是一个高阶线性常系数微分方程，而状态方程则是一阶常系数微分方程组。
在本章里，主要讨论系统的输入-输出方程。
2．系统的起始状态和初始状态的关系？起始状态：通常又称0-状态，它是指系统在激励信号加入之前的状态，包含了全部“过去”的信息（一般地，我们认为激励信号都是在零时刻加入系统的）。
初始状态：通常又称0+状态，它是指系统在激励信号加入之后的状态。
起始状态是系统中储能元件储能情况的反映。
一般用电容器上的电压(0)c v -和电感中的电流(0)L i -来表示电路的储能情况。
若电路的输入信号中没有冲激电流或阶跃电压，则0时刻状态转换时有：(0)(0)c c v v +-= 和 (0)(0)L L i i +-=3．零输入响应和零状态响应的含义？零输入响应和零状态响应是根据系统的输入信号和起始状态的性质划分的。
如果系统无外加输入信号（即输入信号为零）时，由起始状态所产生的响应（也可以看作为由起始状态等效的电压源或电流源----等效输入信号所产生的响应）， 称为零输入响应， 一般用()zi y t 表示；如果系统起始无储能，系统的响应只由外加信号所产生，称为零状态响应， 一般用()zs y t 表示。
根据等效原理，系统的起始储能也可以等效为输入信号，根据系统的线性性质，系统的响应就是零输入响应与零状态响应之和。
4．冲激响应与阶跃响应的关系和意义？冲激响应与阶跃响应都属于零状态响应，而且分别是特殊激励条件下的零状态响应。
冲激响应：是系统在单位冲激信号()t δ激励下的零状态响应。
对线性时不变系统，一般用()h t 表示，而且利用()h t 可以确定系统的因果性和稳定性。
当0t <时，若()0h t =， 则此系统为因果系统；反之，系统是非因果的。
若|()|h t dt ∞-∞<∞⎰， 则此系统为稳定系统。
反之，系统是不稳定的。
阶跃响应：是系统在单位阶跃信号()u t 激励下的零状态响应。
对线性时不变系统，一般用()g t 表示。
根据 ()()t u t d δττ-∞=⎰， 有()()tg t h d ττ-∞=⎰ 或： 根据()()du t t dt δ=，有()()dg t h t dt= 5．卷积积分的意义？卷积积分定义为： ()()*()()()y t x t h t x h t d τττ+∞-∞==-⎰其意义在于：将信号分解为冲激信号之和，借助系统的冲激响应()h t ，求解线性时不变系统对任意激励信号的零状态响应()zs y t 。
在数学计算时，一般分为5个步骤：Step1：变量代换， 将给定信号的自变量t 转换为τ ；例如：()(),()()x t x h t h ττ→→Step2：反褶，把两个参与卷积运算的信号中的一个信号反褶；例如：()()h h ττ→-Step3：平移，把反褶后的信号沿横轴（时间轴）τ 位移t ；例如：()()h h t ττ-→-Step4：乘积，把变换后的两信号相乘； 例如：()()x h t ττ-Step5：积分，根据位移不同导致的信号乘积的不同结果，在非零区间进行积分运算； 即21()()t t x h t d τττ-⎰。
第三章 傅里叶变换分析1．什么是频谱？如何得到信号的频谱？目前我们熟悉的是信号幅度随着时间变化而变化的常见表示方式，比如正弦信号的幅度随着时间按正弦函数的规律变化；另一方面，对于正弦信号，如果知道其振幅、频率和相位，则正弦信号的波形也惟一确定。
根据这个原理和傅里叶级数理论，满足一定条件的周期信号都可以分解为不同频率的正弦分量的线性组合，从而我们用各个正弦分量的频率-幅度、频率-相位来表示周期信号的描述方式就称为周期信号的频谱表示，随着对信号研究的深入，我们将周期信号的频谱表示又推广到非周期信号的频谱表示，即通常的傅里叶变换。
对于周期信号，其频谱一般用傅里叶级数表示，而傅里叶级数的系数就称为信号的频谱：()0110111()cos sin cos()T n n n n n n f t a a n t b n t c c n t ωωωϕ∞∞===++=++∑∑或 1()jn t T n n f t F e ω∞=-∞=∑其中： 122001() 0,1,2,...,1() 1,2, (2)Tjn t T n T n n n F f t e dt n T F a jb n F a ω--==±±±∞=-=∞=⎰对于非周期信号，其频谱一般用傅里叶变换表示：1()()2j t f t F j e d ωωωπ∞-∞=⎰ 其中： ()() j t F j f t e dt ωω∞--∞=⎰2．周期信号和非周期信号的频谱有何不同？周期信号的频谱可以用傅里叶级数表示，它是离散的、非周期的和收敛的。
而非周期信号的频谱用傅里叶变换表示，它是连续的、非周期的和收敛的。
若假设周期信号为()T f t ， 非周期信号为0() ()220 otherwiseT T T f t t f t ⎧-<≤⎪=⎨⎪⎩，并假设周期信号()T f t 的傅里叶级数的系数为n F ，非周期信号0()f t 的傅里叶变换为()F j ω，则有如下的关系：1211()|()|n n n TF F j F j T T ωωπωωω====3．吉伯斯现象是如何产生的？当周期信号存在不连续点时，如果用傅里叶级数逼近，则不论用多少项傅里叶级数，只要不是所有项，则在不连续点必然有起伏，且其起伏的最大值将趋近于一个常数，大约等于不连续点跳变值的8.95%， 我们称这种现象为吉伯斯现象。
4．傅里叶变换的对称性如何应用？傅里叶变换的对称性是指：若 ()() ()|()|j f t F j F j e ϕωωω↔=则 ()() ()|()|j f t F j F j e ϕωωω--↔-=-；**()() ()|()|j f t F j F j e ϕωωω--↔-=-**()() ()|()|j f t F j F j e ϕωωω--↔=从而应用傅里叶变换的线性性质：实信号的傅里叶变换具有共轭对称性，即实信号的幅度谱具有偶函数的特点，而相位谱具有奇函数的特点。
实际中我们应用的基本都是实信号和实系统， 因而在频域分析时基本上都用到这一特性。
例如：某实系统的频响特性是：()()|()|h j H j H j e ϕωωω=；输入的是实信号，具有频谱：()()|()|x j X j X j e ϕωωω= 从而输出的也是实信号，且频谱为：[()()]()|()||()|h x j Y j H j X j e ϕωϕωωωω+=5．傅里叶变换的对偶性有何意义？傅里叶变换的对偶性建立了信号的时域表示波形和频域表示波形之间的对偶特点，即信号的表示形式不论是哪一种，在对信号的信息表示方面是等价的。
