信号完整性分析基础之八——抖动的频域分析
- 格式:docx
- 大小:262.40 KB
- 文档页数:3

振动信号的频谱分析与故障诊断频谱分析是一种常用的信号处理技术,可以对振动信号进行分析和故障诊断。
本文将介绍频谱分析的原理和应用,并探讨其在故障诊断中的作用。
一、频谱分析的原理频谱分析是将一个信号分解成一系列频率成分的过程。
它基于傅里叶变换原理,将时域上的信号转换为频域上的频谱。
通过频谱分析,可以更直观地了解信号的频率特性和频率成分。
在振动信号处理中,频谱分析可以帮助我们获取振动信号的频率谱。
频率谱可以用图形表示,横轴表示频率,纵轴表示振幅。
通过分析频率谱,可以发现信号中的主要频率成分,从而进行故障诊断和分析。
二、频谱分析的方法1. 傅里叶变换(Fourier Transform)傅里叶变换是将信号从时域转换到频域的重要方法。
它将一个连续时域的信号转换为一个连续频域的频谱。
傅里叶变换可以精确地表示信号的频谱信息,但对计算机实现来说,计算量较大。
2. 快速傅里叶变换(Fast Fourier Transform,FFT)为了克服傅里叶变换的计算复杂度,人们提出了快速傅里叶变换算法。
FFT是一种高效的离散傅里叶变换方法,可以在计算机上快速计算信号的频谱。
FFT广泛应用于振动信号处理中,可以实时获得信号的频谱特征。
三、频谱分析在故障诊断中的应用1. 故障特征提取频谱分析可以帮助我们提取振动信号中的故障特征。
不同的故障在频谱上表现出不同的频率成分和振幅分布。
通过比较正常信号和故障信号的频谱特征,可以判断故障类型和程度。
2. 故障诊断频谱分析可以根据特定故障的频率特征,对故障进行诊断。
例如,对于轴承故障,通常会在频谱上出现与旋转频率相关的峰值,通过检测这些峰值可以判断轴承是否发生故障。
3. 故障监测与预警通过对振动信号进行实时频谱分析,可以实现故障的监测与预警。
当频谱中出现异常的频率成分时,说明设备可能存在故障隐患,及早发现并采取措施进行维修,可以避免设备故障进一步恶化。
四、频谱分析的局限性频谱分析虽然是一种有效的振动信号处理方法,但也存在一定的局限性。


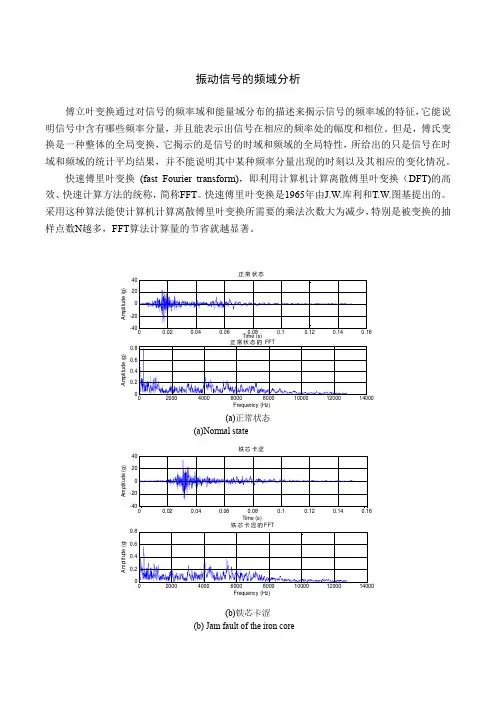
振动信号的频域分析傅立叶变换通过对信号的频率域和能量域分布的描述来揭示信号的频率域的特征,它能说明信号中含有哪些频率分量,并且能表示出信号在相应的频率处的幅度和相位。
但是,傅氏变换是一种整体的全局变换,它揭示的是信号的时域和频域的全局特性,所给出的只是信号在时域和频域的统计平均结果,并不能说明其中某种频率分量出现的时刻以及其相应的变化情况。
快速傅里叶变换 (fast Fourier transform),即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称,简称FFT 。
快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。
采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是被变换的抽样点数N 越多,FFT 算法计算量的节省就越显著。
(a)正常状态(a)Normal state(b)铁芯卡涩(b) Jam fault of the iron coreTime (s)A m p l i t u d e (g )正常状态Frequency (Hz)A m p l i t u d e (g )Time (s)A m p l i t u d e (g )铁芯卡涩Frequency (Hz)A m p l i t u d e (g )铁芯卡涩的FFT(c)润滑不良(c) Lack of mechanical lubrication(d)螺丝松动(d) Base screw looseness图2-6 振动信号的FFT 变换Fig. 2-5 The FFT transform of vibration signal如图2-6所示为振动信号的FFT 变换,从图中可以看出振动信号的频率分布,正常信号和不同故障信号的频率成分和不同频率成分的幅值差异不大,因此,仅利用频域信号提取不同故障信号的特征,并对断路器不同故障进行分类并不可行,应同时考虑频域和时域特征,对振动信号进行时频分析,时频分析方法有小波分析、经验模态分解和局部均值分解((Local Mean Decomposition, LMD)等算法。


振动频谱分析基础振动频谱分析是通过将信号分解成不同频率的成分来研究振动信号的一种方法。
它被广泛应用于机械、航空航天、电力等行业,用于故障诊断、结构健康监测、产品品质评估等方面。
本文将介绍振动频谱分析的基础知识,包括时间域分析、频域分析和谱线类型等内容。
时间域分析是振动频谱分析的起点,它主要研究振动信号在时间轴上的变化。
时间域分析的常用方法有时域图、波形图和轨迹图等。
时域图是通过将振动信号的幅值随着时间的变化绘制成图像来描述信号的特征。
波形图是将振动信号的振动轨迹绘制成图像,可以直观地观察信号的振动形态。
轨迹图则是绘制振动信号的相位随时间的变化,可以用来研究信号的相位关系。
频域分析是振动频谱分析的核心,它通过将信号从时域转换到频域来研究振动信号的频率特性。
频域分析的常用方法有傅里叶变换、快速傅里叶变换(FFT)和功率谱密度分析等。
傅里叶变换是将信号从时域转换到频域的数学方法,可以将信号分解成不同频率的正弦波成分。
FFT是傅里叶变换的一种快速计算方法,可以高效地计算出信号的频谱。
功率谱密度分析则是研究信号能量在不同频率上的分布,可以用来研究信号的频率特性。
在频域分析中,振动信号的频谱可以分为连续谱和离散谱两种类型。
连续谱是指信号在整个频率范围上的分布情况,可以用来分析信号的频带宽度和幅值特性。
离散谱则是指信号在离散频率点上的幅值分布,可以用来研究信号的谐波成分。
在实际应用中,通常使用功率谱来表示振动信号的频谱特性,它是信号在不同频率上的能量密度。
振动频谱分析中的一项重要应用是故障诊断。
通过分析振动信号的频谱可以识别出机械系统中的故障特征,例如轴承故障、齿轮故障等。
不同故障类型会在频谱上产生不同的特征频率,通过识别这些特征频率可以准确地判断故障类型和故障程度。
此外,振动频谱分析还可以用于结构健康监测和产品品质评估等方面,通过对振动信号的频谱进行分析可以得到结构的固有频率和模态参数,评估结构的健康状况和产品的品质水平。

信号完整性分析基础系列之十——理解串行数据测试中的总体抖动算法张昌骏 美国力科公司深圳代表处在高速串行数据的测试中,抖动的测试非常重要。
在串行数据的抖动测试中,抖动定义为信号的边沿与其参考时钟之间的偏差。
对于抖动测量值的量化,通常有抖动的峰峰值和有效值这两个参数。
不过,抖动的峰峰值随着测量时间的增加,测量值不断变大,不能将抖动值与误码率直接联系起来,所以对于抖动测试,抖动的峰峰值并不是一个理想的指标来很衡量器件和系统的性能。
总体抖动(Total Jitter ,简称Tj )为某误码率(Bit Error Ratio ,简称BER )下抖动的峰峰值,在很多串行数据的规范中通常需要测量误码率为的Tj ,简写为Tj@BER=10e-12。
对于BER 小于10e-8的Tj 的测量,通常只有误码率测试仪BERT 可以直接测量到。
对于示波器,假设该高速信号为2.5Gbps 的PCIe ,单个bit 的时长为Unit interval = 400ps ,假设示波器采样率为20G 采样率,则1个bit 上包括了400ps/50ps = 8个采样点,一次分析1M 个bit 需要8M 的存储深度,如果要测量10个比特的抖动,需要让示波器在8M 的存储深度下扫描100次,由于示波器在8Mpts 时计算抖动已经很耗时,重复100次的测试时间会非常长。
所以示波器测量小于的误码率时的总体抖动必须通过某些算法来估算Tj 。
1210−81210−图1:TIE 抖动图示与抖动概率密度函数(PDF )基于示波器求解抖动的算法通常在三个领域观察和分析,即时域、频域、统计域。
比如TIE track 即为TIE 抖动在时域的函数;在频域分析抖动的频谱,可以计算周期性抖动Pj 和随机抖动Rj ;TIE 直方图、Tj 的概率密度函数(Probability Density Function ,简称PDF )是在统计域来分析抖动。
对于总体抖动的计算,通常从统计域分析,即分析抖动的直方图、概率密度函数PDF 和累计分布函数(Cumulative Distribution Function ,简称CDF )。

*四、振动的分解
一个复杂的振动可以是由两个或两个以上的简谐振动所合成。
把有限个或无限个周
期分别为T ,T/2,T/3,…
(或角频率分别为w,2w,
3w,…)的简谐振动合成
起来,所得合振动也一
定是周期为T 的周期性
振动。
医学物理学将复杂的周期性振动分解为一系列简谐振动的操作,称为频谱分析。
将每项的振幅A 和对应的角频率w 画成图线,就是该复杂振动的频谱(frequency spectrum ),其中每一条短线称为谱线。
w
O A
周期性函数 f (t ) 的傅里叶级数可表示为
10n n n t n A A t f )
(cos )( w
医学物理学频谱分析用于发声、听觉、心电图和脑电图等定量分析中,频谱图可为诊断各种疾病提供依据。
频谱分析。

震动信号的频域分析及特征提取研究近年来,随着现代化工业的发展以及基础设施建设的不断推进,人类的生产和生活与机械设备紧密相连,振动问题逐渐成为工程领域中的重要难题。
震动信号的频域分析及特征提取研究,正是针对这一问题而展开的一种重要研究方向。
一、震动信号的频域分析频域分析,是指将时域信号转换为频域信号,从而更深入地研究信号的特征及物理本质的一种信号分析方法。
在机械振动领域中,采用的最为广泛的分析方法就是频域分析。
首先,震动信号的频域分析需要进行信号采集、滤波和采样三个步骤。
采集信号时,可以将传感器与被测物体进行关联,传感器直接监测被测器件震动的振幅和频率,并输出模拟信号,通过数据采集卡转换为数字信号。
在提取特定频率成分或减少多余噪声时,需要进行数字滤波来优化信号质量。
采样过程中,需要根据所获取的传感器信号,采取适当的时间间隔进行数据采样和储存。
接下来是FFT(快速傅里叶变换)算法的应用。
FFT是一种将时间域信号转换为频域信号的算法,可以在计算机上对信号进行快速的频域变换,分离出原信号中的各个频率分量及其强度,在频谱图上显示出来,从而得出一个完整的频域图像。
如果需要对原始数据进行降噪、滤波或预测,可以通过傅里叶变换、小波变换等算法对其进行进一步的频域分析。
二、震动信号特征提取震动信号特征提取,是指通过算法分析对振动信号中的各种性质进行计算和统计,从而提取出能反映工件运动特性和机械状态的客观指标。
研究特征提取方法,能够有效地评估机械设备的运行状况,提高机械设备的效率,延长机械的使用寿命。
震动信号的特征参数主要包括时间域参数和频域参数两大类。
时间域参数包括波形形态参数和时域统计参数,既可以从整体上反映振动信号的波形水平,也可以从微观特性上揭示振动噪声的随机性和不规则性;频域参数则包括功率谱特征和频域统计特征,对于振动信号的分析具有极其重要的作用。
在实际特征提取过程中,震动信号往往是一个很复杂的非线性系统。

信号完整性分析中抖动的分类信号完整性分析中抖动的分类一、峰峰值抖动、均方根抖动过去多年来用于量化抖动的最常用的方法是峰峰值抖动(Peak-to-peak Jitter)和均方根抖动(Root-Mean-Square Jitter,抖动直方图或者抖动分布的1 或者RMS 值)。
但是由于随机抖动以及非固定抖动的存在,使得抖动的峰峰值随着观察样本数量的增加而增加,因此说峰峰值抖动参数用于衡量固有抖动会很有效,但是衡量随机性抖动却会出现很大误差;相同的道理,由于固有抖动及非高斯性抖动和噪声的存在,使得抖动的直方图或者分布图不呈现完全的高斯分布,因此统计得到的抖动的1σ或者RMS 值不等于真实高斯分布的1 值。
峰峰值抖动和均方根抖动均是对某一类抖动的统计分析指标。
二、相位抖动、周期抖动、相邻周期间抖动由于时钟系统是数字电路系统非常关键的一部分,直接决定了数据信号发送和接收的成败,是整个系统的主动脉,因此时钟的抖动一直备受关注。
描述时钟系统的抖动参量一般分为三类,即相位抖动(Phase jitter)、周期抖动(Period jitter)、相邻周期间抖动(Cycle to cycle jitter).1、相位抖动在数字系统中,两个逻辑电平之间的切换通常伴随着快沿的出现,这些边沿在时序上的不稳定性就叫做相位抖动(phase jitter,有时也叫累积抖动,accumulated jitter,指实际边沿位置与理想边沿位置的偏差,以时间为单位,也可以换算成弧度,角度等);相位抖动是相位噪声在数字域的等效体现,它是离散量,因此只有当边沿存在时候才有定义。
理想边沿位置一般定义在数字信号一个比特位时间间隔的整数倍位置处。
如下图1 所示为某一。
在高速串行数据的测试中,抖动的测试非常重要。
在串行数据的抖动测试中,抖动定义为信号的边沿与其参考时钟之间的偏差。
对于抖动测量值的量化,通常有抖动的峰峰值和有效值这两个参数。
不过,抖动的峰峰值随着测量时间的增加,测量值不断变大,不能将抖动值与误码率直接联系起来,所以对于抖动测试,抖动的峰峰值并不是一个理想的指标来很衡量器件和系统的性能。
总体抖动(Total Jitter,简称Tj)为某误码率(Bit Error Ratio,简称BER)下抖动的峰峰值,在很多串行数据的规范中通常需要测量误码率为10e-12的Tj,简写为Tj@BER=10e-12。
对于BER小于10e-8的Tj的测量,通常只有误码率测试仪BERT可以直接测量到。
对于示波器,假设该高速信号为2.5Gbps的PCIe,单个bit的时长为Unit interval = 400ps,假设示波器采样率为20G采样率,则1个bit上包括了400ps/50ps = 8个采样点,一次分析1M个bit需要8M的存储深度,如果要测量10个比特的抖动,需要让示波器在8M的存储深度下扫描100次,由于示波器在8Mpts时计算抖动已经很耗时,重复100次的测试时间会非常长。
所以示波器测量小于10e-12的误码率时的总体抖动必须通过某些算法来估算Tj。
图1:TIE抖动图示与抖动概率密度函数(PDF)基于示波器求解抖动的算法通常在三个领域观察和分析,即时域、频域、统计域。
比如TIE track即为TIE抖动在时域的函数;在频域分析抖动的频谱,可以计算周期性抖动Pj和随机抖动Rj;TIE直方图、Tj的概率密度函数(Probability Density Function,简称PDF)是在统计域来分析抖动。
对于总体抖动的计算,通常从统计域分析,即分析抖动的直方图、概率密度函数PDF和累计分布函数(Cumulative Distribution Function,简称CDF)。
抖动成分及其产生原因分析抖动是数字系统的信号完整性测试的核心内容之一,是时钟和串行信号的最重要测量参数(注:并行总线的最重要测量参数是建立时间和保持时间)。
一般这样定义抖动:“信号的某特定时刻相对于其理想时间位置上的短期偏离为抖动”(参考:Bell Communications Research,Inc(Bellcore),"Synchrous Optical Network(SONET) Transport Systems:Common Generic Criteria,TR-253-CORE",Issue 2, Rev No.1, December 1997".如图1所示。
其中快过10HZ的偏离定义为抖动(Jitter),漫过10Hz的偏离定义为漂移(Wander)。
图1. 时钟和数据抖动的定义抖动和相位噪声和频率噪声有什么关系呢?图2.抖动和相位噪声和频率噪声的关系随着信号速率的不断提高和对精度的越来越高要求,需要进行抖动成分的分离以更深入表征抖动特征和查找问题根源。
一般按图3进行抖动成分的分离。
图3.抖动成分分离图Total Jitter(TJ):总体抖动;Random Jitter(RJ):随机抖动;Deterministic Jitter(DJ):确定性抖动;Data Dependent Jitter(DDJ):数据相关抖动;Periodic Jitter(PJ):周期性抖动;Inter-symbol Interference(ISI):码间干扰Duty Cycle Distortion(DCD):占空比失真;Sub Rate Jitter(SRJ):子速率抖动。
下面分别讨论每种抖动成分的特征和产生原因。
1、随机抖动RJ随机抖动是不能预测的定时噪声,因为它没有可以识别的模式。
典型的随机噪声实例是在无线电接收机调谐到没有活动的载频时听到的声音。
尽管在理论上随机过程具有任意概率分布,但我们假设随机抖动呈现高斯分布,以建立抖动模型。
振动信号频域指标解释说明1. 引言1.1 概述振动信号频域指标是用于分析和评估振动信号特征的一种重要方法。
随着科技的发展和应用领域的不断扩大,对机械设备和工业系统的故障诊断、状态监测以及振动信号处理的需求也越来越高。
频域分析作为一种常用的信号分析方法,可以提供关于信号频率和能量分布的详细信息,从而帮助我们更好地理解和解释振动信号的特性。
1.2 文章结构本文将从以下几个方面对振动信号频域指标进行解释说明。
首先,在第二部分中,我们将介绍振动信号频域表示以及傅里叶变换的基本原理,并探讨其在工程实践中的应用。
接下来,在第三部分中,我们将介绍常见的振动信号特征提取方法,包括时间域特征提取方法、频域特征提取方法以及小波变换与振动信号特征提取之间的关系。
然后,在第四部分中,我们将通过具体案例分析,探讨振动信号频域指标在故障诊断、机械设备状态监测以及工业振动信号处理中的实际应用情况。
最后,在第五部分中,我们将对全文进行总结回顾,并展望未来研究方向。
1.3 目的本文旨在深入介绍和解释振动信号频域指标的原理和应用,帮助读者更好地理解和应用频域分析方法,促进相关领域的研究和发展。
通过学习本文内容,读者将能够掌握振动信号频域表示、傅里叶变换及其应用、特征提取方法以及频域指标在故障诊断、状态监测和工业振动信号处理中的实际案例应用等知识,并能够对未来相关研究方向进行展望。
2. 频域分析2.1 振动信号频域表示在振动信号分析中,频域是一种重要的分析手段。
频域分析是通过将时域的振动信号转换成频域表示来研究信号的特征和性质。
频域表示可以将振动信号分解成一系列不同频率的正弦波成分,从而更好地理解和描述信号在不同频率上的能量分布。
2.2 傅里叶变换及其应用傅里叶变换是一种常用的数学工具,用于将时域信号转换为频域。
它可以将周期性或非周期性信号拆解为若干个正弦和余弦函数,并得到各个频率成分对应的幅值和相位信息。
傅里叶变换在振动信号处理中广泛应用,可以提供关于振动信号频谱内容的详细信息。
抖动产生及测试一、信号完整性测试手段抖动测试、波形测试、眼图测试,是三种常用的信号完整性测试。
1.抖动测试:抖动测试现在越来越受到重视,因为专用的抖动测试仪器,比如TIA(时间间隔分析仪)、SIA3000,价格非常昂贵,使用得比较少。
使用得最多是示波器加上软件处理,如TEK 的TDSJIT3 软件。
通过软件处理,分离出各个分量,比如RJ 和DJ,以及DJ 中的各个分量。
对于这种测试,选择的示波器,长存储和高速采样是必要条件,比如2M 以上的存储器,20GSa/s 的采样速率。
不过目前抖动测试,各个公司的解决方案得到结果还有相当差异,还没有哪个是权威或者行业标准。
2.波形测试首先是要求主机和探头一起组成的带宽要足够。
基本上测试系统的带宽是测试信号带宽的3 倍以上就可以了。
实际使用中,有一些工程师随便找一些探头就去测试,甚至是A 公司的探头插到B 公司的示波器去,这种测试很难得到准确的结果。
波形测试是信号完整性测试中最常用的手段,一般是使用示波器进行,主要测试波形幅度、边沿和毛刺等,通过测试波形的参数,可以看出幅度、边沿时间等是否满足器件接口电平的要求,有没有存在信号毛刺等。
由于示波器是极为通用的仪器,几乎所有的硬件工程师都会使用,但并不表示大家都使用得好。
波形测试也要遵循一些要求,才能够得到准确的信号。
其次要注重细节。
比如测试点通常选择放在接收器件的管脚,如果条件限制放不到上面去的,比如BGA封装的器件,可以放到最靠近管脚的PCB 走线上或者过孔上面。
距离接收器件管脚过远,因为信号反射,可能会导致测试结果和实际信号差异比较大;探头的地线尽量选择短地线等。
最后,需要注意一下匹配。
这个主要是针对使用同轴电缆去测试的情况,同轴直接接到示波器上去,负载通常是50 欧姆,并且是直流耦合,而对于某些电路,需要直流偏置,直接将测试系统接入时会影响电路工作状态,从而测试不到正常的波形。
3.眼图测试眼图测试是常用的测试手段,特别是对于有规范要求的接口,比如E1/T1、USB、10/100BASE-T,还有光接口等。
高速信号完整性测试之抖动分析和眼图JITTER ANAL YSIS&EYE DIAGRAM高速信号完整性测试的意义随着电子技术的飞速发展,数字信号的传输速率不断提升,码元周期(一个码元的持续时间或周期)越来越窄。
使得信号在传输过程中更容易受到各种干扰和损耗。
信号完整性测试能够帮助工程师准确评估信号质量,预测系统在实际运行中的性能,从而在设计阶段就避免潜在的问题。
通过信号完整性测试,可以优化电路设计、选择合适的元器件和布线方式,提高系统的抗干扰能力和稳定性。
高速串行总线介绍优势:1.并行总线时钟速率物理限制在1GHz至2GHz左右,因为单个时钟和数据线引入的偏斜会在更高的速率下导致误码。
串行总线有效的解决了这个问题;2.以差分信号进行传输,有很高的共模抑制比;3.使用嵌入式时钟,免除时钟与数据传输的延时误差;4.多条串行链路可以连贯地捆绑在一起,使之有更高的数据吞吐量,PCB布线也更加简洁;5.更长的传输距离,更快地传输速度。
如USB3.2单条lane传输速率可以达到10Gbps,更高的USB4.0可以达到20Gbps。
劣势:1.码元周期越来越窄,信号高于5Gbps时,信号质量会给模拟设计带来极大的挑战;码元:数字通信系统中的基本单位,一个码元可包括一位二进制数“1”、“0”,也可包括二位二进制数“00”、“01”、“10”、“11”,当然也可包括三位及以上二进制数。
这个码元的持续时间长度就是码元周期,码元周期越窄,信号速率越高,因为单位时间内传输更多的码元需要更短的码元周期。
2.需要使用高质量的PCB、连接器和线缆才能保证高速信号完美的传输;3.设计高速串行链路时需要考虑采用合适的技术来最大限度地减少信号失真;在如此快速的信号环境中,信号完整性测试就变得尤为重要。
特别是数据的抖动以及使用眼图进行信号质量的评估,是工程师最常用最直接的方法。
高速信号中的抖动抖动的概念:抖动指的是信号理想边沿和实际边沿之间的偏差。
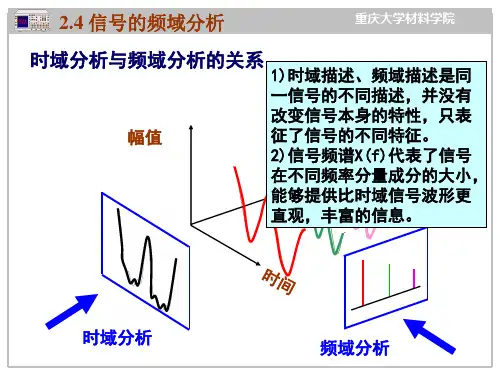
频域分析频域(频率域)——自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。
频谱图描述了信号的频率结构及频率与该频率信号幅度的关系。
对信号进行时域分析时,有时一些信号的时域参数相同,但并不能说明信号就完全相同。
因为信号不仅随时间变化,还与频率、相位等信息有关,这就需要进一步分析信号的频率结构,并在频率域中对信号进行描述。
动态信号从时间域变换到频率域主要通过傅立叶级数和傅立叶变换实现。
周期信号靠傅立叶级数,非周期信号靠傅立叶变换。
举例一个频域分析的简例可以通过图1:一个简单线性过程中小孩的玩具来加以说明。
该线性系统包含一个用手柄安装的弹簧来悬挂的重物。
小孩通过上下移动手柄来控制重物的位置。
任何玩过这种游戏的人都知道,如果或多或少以一种正弦波的方式来移动手柄,那么,重物也会以相同的频率开始振荡,尽管此时重物的振荡与手柄的移动并不同步。
只有在弹簧无法充分伸长的情况下,重物与弹簧会同步运动且以相对较低的频率动作。
随着频率愈来愈高,重物振荡的相位可能更加超前于手柄的相位,也可能更加滞后。
在过程对象的固有频率点上,重物振荡的高度将达到最高。
过程对象的固有频率是由重物的质量及弹簧的强度系数来决定的。
当输入频率越来越大于过程对象的固有频率时,重物振荡的幅度将趋于减少,相位将更加滞后(换言之,重物振荡的幅度将越来越少,而其相位滞后将越来越大)。
在极高频的情况下,重物仅仅轻微移动,而与手柄的运动方向恰恰相反。
Bode图所有的线性过程对象都表现出类似的特性。
这些过程对象均将正弦波的输入转换为同频率的正弦波的输出,不同的是,输出与输入的振幅和相位有所改变。
振幅和相位的变化量的大小取决于过程对象的相位滞后与增益大小。
增益可以定义为“经由过程对象放大后,输出正弦波振幅与输入正弦波振幅之间的比例系数”,而相位滞后可以定义为“输出正弦波与输入正弦波相比较,输出信号滞后的度数”。
与稳态增益K值不同的是,“过程对象的增益和相位滞后”将依据于输入正弦波信号的频率而改变。
在上两篇文章中,我们分别介绍了直方图(统计域分析)和抖动追踪(时域分析)在抖动分析中的应用。
从抖动的直方图和抖动追踪波形上我们可以得到抖动的主要构成成分以及抖动参数的变化趋势。
如需对抖动的构成做进一步的分析,还需要从频域角度去进一步分析抖动的跟踪波形。
抖动的频谱即是对抖动追踪(jitter track)波形做FFT运算。
如下图1所示
为一个时钟周期测量参数的追踪、频谱分析步骤及效果,在抖动频谱图上可以清楚的看出某两个频率值点抖动比较大:
图1 抖动频谱
黄色为实际采集到的时钟波形(C1通道)
P1测量C1通道时钟信号的时钟周期
F7函数对P1测量参数进行跟踪
F6对F7进行FFT分析
下图2所示为一典型的串行信号抖动追踪频谱图,从图中可看出各种抖动成分;DDj和Pj为窄带频谱(三角形谱或者谱线)但是DDj和Pj的区别是由于DDj是和码型相关的,其频率fDDJ一般会是数据位率的整数倍,如果Pj的频率fPJ正好等于fDDJ,那么从抖动的频谱图里面是很难将DDj和Pj精确的分开的,所以通常在抖动分解的过程中一般通过时域平均的方法来分解DDj;BUj主要由于串扰等因素引起的,一般分为两种,一种是窄带,但幅度较高,很显然这类BUJ也是很难和PJ区分开的,除非我们知道引起BUJ的源头,知道其频率,所以说我们在抖动测试时得到的PJ一般会包含这类BUJ(所以通常情况下对这类BUJ不加区分,直接算做PJ,而将BUJ分类为PJ和OBUJ,在之前的抖动分类文章中有提及);另外一类是宽带的BUJ(很多时候也叫OBUJ,other bounded uncorrelated jitter),幅度很小,基本会埋没到RJ中去,这类抖动很容易被误算作RJ,目前使用在示波器上的抖动分解软件只有Lecroy最近推出的SDAII(基于NQ-SCALE抖动分解理论)能够较好的将这类抖动从Rj中剥离出来;RJ是
宽带频谱,幅度很小。
图2 典型的数据抖动频谱图构成
在Lecroy示波器的SDAII抖动分析软件中,是先通过时域平均的方法分离出DDJ.然后在对抖动追踪波形做FFT分析。
因此剥离了DDJ以后的FFT频谱只包含了RJ+BUJ成份(注:此BUJ包含PJ和OBUJ),如下图3所示:
图3 RJ+BUJ Spectrum
从上图3中,我们看到有一条黄色的门限曲线,门限曲线以上的谱线为Pj,谱线以下的为Rj+OBUJ。
这条门限曲线是通过图中的一个包含200个点的小滑窗在整个频谱图上从左到右依次滑动,对每个小窗口中的样本点求median(中值),因为我们知道对于RJ来说,其median值应该为零(当然是当样本数量达到一定数量以后,所以说示波器里所用的200个样本点的滑窗也就是这个道理)。
如果将OBUJ也当作RJ来处理,那么只要将门限曲线以下的部分求积分(平均功率)就可得到Rj的值了。
目前其它示波器厂家计算RJ用的就是这样的办法,忽略了OBUJ的存在,测得的RJ值会略有偏大(当OBUJ存在的时候)。
Lecroy
示波器的SDAII抖动分析软件包包括了两种方法,一种就和上面的类似(叫dual-dirac spectral),计算得到的Rj会略有偏大;另外一种能够通过NQ-SCALE 的理论将OBUJ有效的从RJ频谱中剥离出来,这个方法叫dual-dirac NQ-Scale,测量得到的RJ会更加精确。
如下图4、5所示:
图4 Dual-Dirac Spectral 方法测得的Rj值(10.1ps)
图
5 Dual-Dirac NQ-Scale 方法测得的Rj值(2.0ps)。