拉格朗日插值法1

拉格朗日插值法解题步骤：
拉格朗日插值法是一种数学方法，用于通过已知的离散数据点来构造一个多项式，这个多项式可以用来估计或逼近其他未知的数据点。

以下是拉格朗日插值法的解题步骤：
1.确定已知数据点：首先，你需要有一组已知的数据点。

这些数据点是你用来进行插值的已知信息。

2.构造拉格朗日多项式：对于每一个数据点 (xi, yi)，构造一个拉格朗日基函数。

3. 计算拉格朗日多项式的值：将每个已知数据点的横坐标xi 代入拉格朗日多项式L(x)，得到对应的yi 值。

这样，你就可以得到一个新的数据点集，这些点的坐标是(xi, L(xi))。

4. 使用插值多项式进行预测：对于你想要预测的x 值，代入拉格朗日多项式L(x)，即可得到对应的y 值。

这就是拉格朗日插值法的基本步骤。

需要注意的是，这种方法只适用于已知的数据点是离散的情况。

如果数据点是连续变化的，你可能需要使用其他方法，如样条插值等。

拉格朗日插值法就是构造一个多项式，使得恰好在每一个x处取到对应的y
首先，n+1个点(xi,yi)若xi不同，则可以确定唯一的最高幂次不超过n的多项式。

而如果题目直接或是间接给出了n+1个点，让我们求由这些点构成的多项式在某一个位置的取值，那么应用拉格朗日插值可以在O(n2 )的时间内解决这一问题
思路如下：
对于这个函数，要想在k=x[i]的时候取到y[i]，并且y[i]仅在这一情况对答案有影响，就要构造出一项K[i]y[i],使得x仅在取到x[i]时K为1,其他情况K[i]为0。

于是，仿照中国剩余定理的思路，有了如下构造方式：
(1)首先，x≠x[i]时K[i]为0，就要让x取到除去x[i]外的任何值都为0，于是有了“累乘‘k-x[j]’”的思路；
(2)其次，如果简单地将y[i]与累乘‘k-x[j]’结合，则x=x[i]时
该项为“累乘x[i]-x[j]",所以需要在每一项下面加上"除以x[i]-x[j]”
(3)最后将每一项加和，得到上式
拓展：x取值连续时的做法
有时候，问题仅要求求解x连续的情况。

那么如果仅有一个k值需要代入f(k)，就可以用下面的方法将复杂度变为
O(n)
对于分子，维护出k的前缀积和后缀积，即：
由于最终求得的值一定为正数，故需判断一下正负号。

如果N-i为奇数，则分母要取负数（因为fac(N-i)表示的是绝对值，N-i为偶数的时候恰好所有负号消掉了）。

常见的插值方法及其原理1. 拉格朗日插值法（Lagrange Interpolation）拉格朗日插值法是一种基于多项式的插值方法，通过n+1个已知点的函数值来构造一个n次多项式。

具体的计算公式如下：L(x) = Σ[yk * lk(x)], k=0 to n其中yk为已知点（xi, yi）的函数值，lk(x)为拉格朗日基函数，定义为：lk(x) = Π[(x - xj)/(xi - xj)], j=0 to n, j≠k拉格朗日插值法的原理是通过构造一个通过已知点的n次多项式，来代替未知函数的近似值。

利用拉格朗日基函数的性质，可以保证插值多项式通过已知点。

2. 牛顿插值法（Newton Interpolation）牛顿插值法是一种递推的插值方法，通过已知点的函数值和差商来逐步构造插值多项式。

差商的定义如下：f[x0]=y0f[x1]=(f[x1]-f[x0])/(x1-x0)f[x2]=(f[x2]-f[x1])/(x2-x1)...f[xn] = (f[xn] - f[xn-1]) / (xn - xn-1)利用差商的定义，可以得到牛顿插值多项式的表达式：N(x) = f[x0] + f[x0, x1](x-x0) + f[x0, x1, x2](x-x0)(x-x1) + ... + f[x0, x1, ..., xn](x-x0)(x-x1)...(x-xn)牛顿插值法的原理是通过递推计算差商来得到插值多项式。

通过使用差商来处理已知点的函数值差异，可以得到更高次的插值多项式。

3. 样条插值法（Spline Interpolation）样条插值法是一种基于分段低次插值函数的插值方法，常用的是三次样条插值。

样条插值法通过寻找一组分段函数，使得满足原函数的插值条件，并要求函数在每个插值点处的函数值、一阶导数和二阶导数连续。

这样可以保证插值函数在每个插值点处的平滑性。

三次样条插值法的原理是将整个插值区间划分为多个小区间，在每个小区间内使用三次多项式进行插值。

拉格朗⽇（Lagrange）插值算法拉格朗⽇插值（Lagrange interpolation）是⼀种多项式插值⽅法，指插值条件中不出现被插函数导数值，过n+1个样点，满⾜如下图的插值条件的多项式。

也叫做拉格朗⽇公式。

这⾥以拉格朗⽇3次插值为例，利⽤C++进⾏实现：1//利⽤lagrange插值公式2 #include<iostream>3using namespace std;45double Lx(int i,double x,double* Arr)6 {7double fenzi=1,fenmu=1;8for (int k=0;k<4;k++)9 {10if (k==i)11continue;12 fenzi*=x-Arr[k];13 fenmu*=Arr[i]-Arr[k];14 }15return fenzi/fenmu;16 }1718int main()19 {20double xArr[4]={};21double yArr[4]={};22//输⼊4个节点坐标23 cout<<"请依次输⼊4个节点的坐标:"<<endl;24for (int i=0;i<4;i++)25 cin>>xArr[i]>>yArr[i];2627//输⼊要求解的节点的横坐标28 cout<<"请输⼊要求解的节点的横坐标:";29double x;30 cin>>x;31double y=0;32for (int i=0;i<4;i++)33 y+=Lx(i,x,xArr)*yArr[i];34 printf("x=%lf时，y=%lf\n",x,y);3536//分界，下⾯为已知y求x37 cout<<"请输⼊要求解的节点的纵坐标:";38 cin>>y;39 x=0;40for (int i=0;i<4;i++)41 x+=Lx(i,y,yArr)*xArr[i];42 printf("y=%lf时，x=%lf\n",y,x);4344 system("pause");45return0;46 }作者：耑新新，发布于转载请注明出处，欢迎邮件交流：zhuanxinxin@。

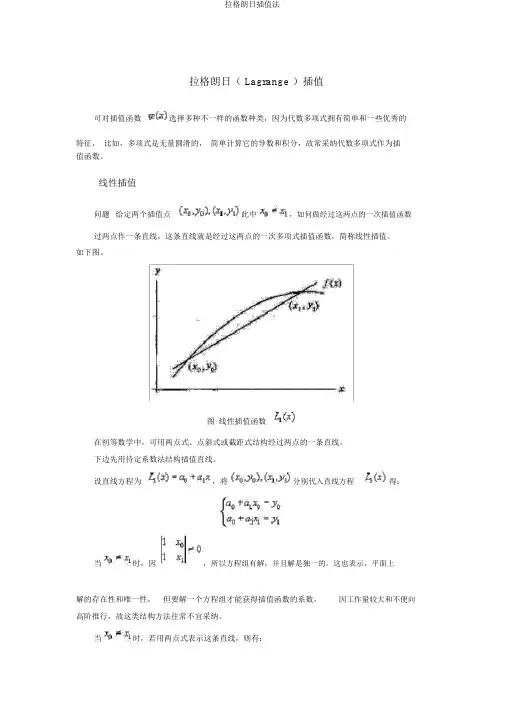
拉格朗日（ Lagrange ）插值可对插值函数选择多种不一样的函数种类，因为代数多项式拥有简单和一些优秀的特征，比如，多项式是无量圆滑的，简单计算它的导数和积分，故常采纳代数多项式作为插值函数。

线性插值问题给定两个插值点此中，如何做经过这两点的一次插值函数过两点作一条直线，这条直线就是经过这两点的一次多项式插值函数，简称线性插值。

如下图。

图线性插值函数在初等数学中，可用两点式、点斜式或截距式结构经过两点的一条直线。

下边先用待定系数法结构插值直线。

设直线方程为，将分别代入直线方程得：当时，因，所以方程组有解，并且解是独一的。

这也表示，平面上解的存在性和唯一性，但要解一个方程组才能获得插值函数的系数，因工作量较大和不便向高阶推行，故这类结构方法往常不宜采纳。

当时，若用两点式表示这条直线，则有：（）这类形式称为拉格朗日插值多项式。

，，称为插值基函数，计算，的值，易见（）在拉格朗日插值多项式中可将看做两条直线，的叠加，并可看到两个插值点的作用和地位都是同等的。

拉格朗日插值多项式型式免去认识方程组的计算，易于向高次插值多项式型式推行。

线性插值偏差定理记为以为插值点的插值函数，。

这里，设一阶连续可导，在上存在，则对随意给定的，起码存在一点，使（）证明令，因是的根，所以可设对任何一个固定的点，引进协助函数：则由定义可得别在和和，即。

，这样起码有上应用洛尔定理，可知和，对3个零点，不失一般性，假设在每个区间起码存在一个零点，不如记为在上应用洛尔定理，获得，分在上起码有一个零点，。

此刻对求二次导数，此中的线性函数)，故有代入，得所以即二次插值问题给定三个插值点，, 此中互不相等，如何结构函数的二次的（抛物线）插值多项式平面上的三个点能确立一条次曲线，如下图。

图三个插值点的二次插值仿制线性插值的拉格朗日插值，即用插值基函数的方法结构插值多项式。

设每个基函数是一个二次函数，对来说，要求是它的零点，所以可设同理，也相对应的形式，得将代入，得同理将代入获得和的值，以及和的表达式。

多项式⼊门——拉格朗⽇插值多项式⼊门——拉格朗⽇插值插值⽤来求解这样⼀类问题：给定 \(n\) 点 \((x_i,y_i)\) 求过这些点的多项式。

1 简介设 \(f(x)\) 为这个多项式，我们有：\[f(x)\equiv f(a)\bmod (x-a)\tag{1} \]这是因为：\[f(x)-f(a)=(a_0-a_0)+a_1(x-a)+a_2(x^2-a^2)+... \]⽽后者显然有⼀个根为 \(a\) ，所以 \((1)\) 式得证。

通过把这 \(n\) 个点代⼊我们可以得到：\[\begin{cases} f(x)\equiv y_1\bmod x-x_1\\ ...\\ f(x)\equiv y_n\bmod x-x_n \end{cases} \]显然模数互质，所以我们考虑⽤中国剩余定理来解决这个事情。

令 \(M=\prod_{i=1}^n(x-x_i)\) ，\(m_i=\frac{M}{x-x_i}=\prod_{i\not= j}(x-x_j)\) 。

并且在模 \(x-x_i\) 的意义下，我们有：\[m_i^{-1}=\frac{1}{\prod\limits_{i\not=j}(x_i-x_j)} \]这是因为我们有：\[\prod_{i\not =j}(x-x_j)\equiv \prod_{i\not =j}(x-x_j-x+x_i)=\prod_{i\not =j}(x_i-x_j) \]所以上述结论成⽴。

所以我们有：\[f(x)\equiv \sum\limits_{i=1}^ny_im_im_i^{-1}\equiv \sum\limits_{i=1}^ny_i\prod\limits_{j\not=i}\frac{x-x_j}{x_i-x_j} \]这个东西可以在 \(n^2\) 的时间内求出。

2 例题直接模拟上⾯的过程即可。

#include<bits/stdc++.h>#define dd double#define ld long double#define ll long long#define uint unsigned int#define ull unsigned long long#define N 2010#define M numberusing namespace std;const int INF=0x3f3f3f3f;const ll mod=998244353;template<typename T> inline void read(T &x) {x=0; int f=1;char c=getchar();for(;!isdigit(c);c=getchar()) if(c == '-') f=-f;for(;isdigit(c);c=getchar()) x=x*10+c-'0';x*=f;}inline ll ksm(ll a,ll b,ll mod){ll res=1;while(b){if(b&1) (res*=a)%=mod;a=a*a%mod;b>>=1;}return res;}inline ll inv(ll a){return ksm(a,mod-2,mod);}ll n,k,x[N],y[N],ans;int main(){read(n);read(k);for(int i=1;i<=n;i++){read(x[i]);read(y[i]);}for(int i=1;i<=n;i++){ll fenzi=1,fenmu=1;for(int j=1;j<=n;j++){if(j==i) continue;fenmu*=(x[i]-x[j]);fenmu%=mod;fenzi*=(k-x[j]);fenzi%=mod;}ans+=y[i]*fenzi%mod*inv(fenmu)%mod;ans%=mod;}printf("%lld\n",(ans%mod+mod)%mod);return 0;}注意：需要把分母乘出来再求逆元，这样复杂度的瓶颈就不会是求逆元。

实验九 Lagrange 插值法求近似函数实验一、实验内容：设2.12)(2+-=x x x f ,数据点取值如下表分别构造)(),(),(432x L x L x L 来近似)(x f .二、算法原理：插值法是函数逼近的一种重要方法，解决对于只提供离散数据点 ))(,(i i i y x f x =, i=0,1,...,n,而希望在函数空间{}n s p a n ϕϕϕ,...,,2=Φ中选择,)(1i ni i c x S ϕ∑==来近似于真实函数)(x f 的问题，其中i c 是可选择参数，可通过要求曲线)(x S 经过数据点，即满足插值条件n i x f x S i i ,...,1,0),()(==来确定.所谓的代数插值指以代数多项式)(x P n 作为插值函数，即函数空间取为 {}n x x s p a n ,...,,1=Φ，代数插值多项式)(x P n 的表达式，在理论上可通过求解参数i c 满足的1+n 个方程⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++n n n n n n n n n n y x c x c x c c y x c x c x c c y x c x c x c c ...... (22101121211000202010)唯一确定，但实际上不可取。

Lagrange 插值法巧妙利用了基函数法，直接构造出该插值多项式 ),()(x P x L n n =它适用于非等距节点.其基本思想是通过满足在节点i x 处值取1，其余处取0的插值基函数),(x l i 将)(x L n 表达为一个线性结合,)()(1i ni i n y x l x L ∑==其中 n i x x x x x l n i j j j i j i ≤≤--=∏≠=0,)(0 具体算法如下Step1输入数据点总数1+n （即输入n 值），节点i x ，相应的函数值i y ，i =0,1,…,n,令;0)(=x L nStep2 for 0=i to n{计算∏≠=--=n i j j j i j i x x x x x l 0)(s=1,for 0=j to n {如果i j =，s s =， 否则， j i j x x x x s s --=})(x l s i →)())()((x L y x l x L n i i n →+ }Step3输出插值多项式)(x L n .三、实验要求：（1）编制Lagrange 插值法程序，得出实验结果，并进行比较；（2）观察高次代数插值的Runge 现象：1901年，德国数学家runge 考察函数22511)(x x f += 在[]1,1- 上n 等分做等距节点插值时，观察到插值节点∞→n ，插值多项式)(x P n 仅在726.0≤x 内收敛于)(x f ，而此区间以外都发散. 请用10=n ，计算Lagrange 插值多项式10P ，通过图示（在一个坐标上画出10P 和)(x f 的对比图） ，观察这一现象， 并写出你所得到的启示.四、源代码：#include<stdio.h>#include<math.h>void main(){int i,j,n=4;float y=0.7,Ln=0;float s;float x[5]={-1,-0.5,0,0.5,1},f[5]={4.2,2.45,1.2,0.45,0.2},l[5];for(i=0;i<=n;i++){s=1;for(j=0;j<=n;j++){if(j==i)s=s;elses*=(y-x[j])/(x[i]-x[j]);}l[i]=s;Ln+=l[i]*f[i];}printf("%f",Ln);}五、实验结果截图：六、上机体会：。

拉格朗⽇插值法（图⽂详解）拉格朗⽇插值⼊门由⼩学知识可知，n个点(x_i,y_i)可以唯⼀地确定⼀个多项式现在，给定n个点，请你确定这个多项式，并将k代⼊求值求出的值对998244353取模Input第⼀⾏两个正整数n,k，含义如题接下来n⾏，每⾏两个正整数x_i,y_i含义如题。

n≤2000,xi,yi,k≤998244353Output⼀个整数表⽰答案Sample Input3 1001 42 93 16Sample Output10201//样例⼀中的三个点确定的多项式是f(x)=x^2+2x+1，将100代⼊求值得到10201int re=1;while(y){if(y&1) re=(x*re)%mod;x=(x*x)%mod;y>>=1;}return re;}int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-')f=-f;ch=getchar();}while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}return x*f;}signed main(){n=read(),k=read();for(int i=1;i<=n;i++)a[i]=read(),b[i]=read();for(int i=1;i<=n;i++){int tmp=1;for(int j=1;j<=n;j++)if(i!=j)tmp=tmp*(a[i]+mod-a[j])%mod; //分母tmp=quickpow(tmp,mod-2);for(int j=1;j<=n;j++)if(i!=j) tmp=tmp*(k+mod-a[j])%mod; //分⼦tmp=tmp*b[i]%mod;ans=(ans+tmp)%mod;}printf("%lld\n",ans);return 0;}#include<bits/stdc++.h>using namespace std;const int mod=998244353;int x[2010],y[2010],a=1,b=0;int powmod(int a,int b){int ans=1;while(b){if(b&1)ans=1ll*ans*a%mod;a=1ll*a*a%mod;b>>=1;}return ans;}int main(){int n,k;scanf("%d%d",&n,&k);for(int i=1;i<=n;i++)scanf("%d%d",x+i,y+i);for(int i=1;i<=n;i++){int a1=1,b1=1;//a1代表分母，b1代表分⼦b1=1ll*b1*y[i]%mod;for(int j=1;j<=n;j++)if(j!=i){b1=1ll*b1*(k-x[j])%mod;a1=1ll*a1*(x[i]-x[j])%mod;}b=(1ll*a1*b+1ll*a*b1)%mod;a=1ll*a*a1%mod;//b/a+b1/a1=(b*a1+a*b1)/(a*a1)}a=(a+mod)%mod,b=(b+mod)%mod;printf("%lld\n",1ll*b*powmod(a,mod-2)%mod);//因为带了除法，所以分母会⽐较⼤，于是在前⾯边乘边取模，最后取逆元return 0;}参考资料。

一阶拉格朗日插值算法是一种数学方法，用于通过已知的离散数据点来构造一个插值多项式。

这种方法在数值分析、计算几何和工程等领域有广泛应用。

假设我们有一组有序的已知数据点(x0, y0), (x1, y1), ..., (xn, yn)，我们想要找到一个多项式P(x)，使得P(xi) = yi，对于i = 0, 1, ..., n。

一阶拉格朗日插值算法的步骤如下：
1. 初始化：令多项式P(x) = 0。

2. 对于i = 0, 1, ..., n，执行以下步骤：
a. 计算拉格朗日基函数Li(x) = (x - xi) / (x - xi)。

注意，当x = xi 时，Li(x) 是未定义的，因此在实际应用中需要处理这种情况。

b. 将Li(x) 乘到P(x) 上，即P(x) = P(x) + y*Li(x)。

3. 返回P(x) 作为插值多项式。

下面是一个使用Python 实现的一阶拉格朗日插值算法的示例代码：
例如，假设我们有三个已知数据点(1, 2), (2, 3), (3, 4)，我们可以调用`lagrange_interpolation([1, 2, 3], [2, 3, 4])` 来得到插值多项式函
数。

然后，我们可以使用这个函数来计算任意x 值对应的插值y 值，例如`lagrange_interpolation([1, 2, 3])(2.5)` 将返回约2.75。

第二章 插值法知识点：拉格朗日插值法，牛顿插值法，误差，龙格现象，分段插值。

1.背景实践活动中，表现事务变化的信息往往只是一些离散点值，例如 每个6小时记录一次温度，以此反映一天的气温变化状况，如下表图能从已知这些离散点值信息知道10时的气温是多少吗？如果能通过这些离散点值找到气温变化的规律，也就是说能找到一个反映气温变化规律的“原”函数，就可以知道10时的气温是多少。

但我们能采集到的信息只有这些离散点值，时常给不出反映气温变化规律“原”函数的解析表达式，怎么办？通常可以用近似的办法解决这个问题，办法是构造一个通过所有离散点值的“近似”函数，用这个“近似”函数逼近“原”函数。

如图构造这个“近似”函数的方法称为插值方法。

34 32 30 28 26 24 22 20时间（时）温度（。

C ）34 32 30 28 26 24 22 20温度（。

C ）2.概念实际问题中，能采集到的信息只是一些离散点值{x i,f(x i)}(i=0,1,2,…n)，时常给不出一个函数f（x）的解析表达式，因之，转而考虑选择一个简单的函数ϕ（x）近似替代（原来）f（x）。

定义：设f（x）为定义在区间[a，b]上的函数，x0,x1,…,x n为[a，b]上的互异点，y i=f（x i）。

若存在一个简单函数ϕ（x），满足（插值条件）ϕ（x i）=f（x i），i=0，1，…，n。

则称 ϕ（x）为f（x）插值函数，f（x）为被插函数,点x0,x1,…,x n为插值节点,点{x i,f(x i)},i=0,1,2,…n为插值点。

若用ϕ（x）≈f（x），则计算f（x）就转换为计算 ϕ（x）。

插值需要解决：插值函数是否存在唯一；插值函数如何构造；插值函数与被插函数的误差估计和收敛性。

对插值函数的类型有多种不同的选择，代数多项式p n(x)常被选作插值函数 ϕ（x）。

P23(2.18)和(2.19)指出，存在唯一的满足插值条件的n次插值多项式p n(x)。