第十一章多元函数积分学

多元函数积分知识点总结1. 多元函数的概念多元函数是指至少含有两个自变量的函数，它是自变量的多项式和、积、商或者反函数的复合函数。

多元函数的自变量可以是实数，也可以是复数。

例如，z=f(x,y)表示一个含有两个自变量的函数，其中x和y称为自变量，z称为因变量。

多元函数的图形通常是在三维坐标系中表示的，它描述了自变量之间的关系和对因变量的影响。

2. 多元函数的积分多元函数的积分是对多元函数在给定区域上的积分运算，它可以表示为对函数在该区域上的所有微小部分进行求和。

多元函数的积分具有广泛的应用，例如在物理学、工程学、经济学等领域中都有重要应用。

多元函数的积分包括二重积分和三重积分两种重要形式。

3. 二重积分二重积分是对二元函数在给定区域上的积分运算，它可以表示为对函数在该区域上的面积进行求和。

二重积分的计算通常涉及到对区域进行分割、确定积分范围、选择合适的坐标系等步骤。

二重积分的求解可以利用极坐标、直角坐标等不同坐标系进行计算，根据具体问题的情况选择合适的坐标系可以简化计算过程。

4. 三重积分三重积分是对三元函数在给定区域上的积分运算，它可以表示为对函数在该区域上的体积进行求和。

三重积分的计算通常涉及到对区域进行分割、确定积分范围、选择合适的坐标系等步骤。

三重积分的求解可以利用柱面坐标、球面坐标等不同坐标系进行计算，根据具体问题的情况选择合适的坐标系可以简化计算过程。

5. 多元函数的积分性质多元函数的积分具有一些重要的性质，包括线性性质、可加性、区域可加性等。

其中线性性质指的是积分运算满足线性运算规律，可加性指的是积分在不同区域的和等于对整个区域的积分，区域可加性指的是积分在求和区域上的分割等价性。

这些性质在多元函数积分的计算中起着重要的作用，可以帮助简化计算过程和求得精确解。

6. 多元函数的变限积分多元函数的变限积分是对多元函数在变化区域上的积分运算，它可以表示为对函数在变限区域上的所有微小部分进行求和。

多元函数的积分在数学中，多元函数的积分是一项重要的概念和计算方法。

与一元函数的积分类似，多元函数的积分可以帮助我们求解曲线下的面积、体积等问题，以及解决一些与实际问题相关的计算。

一、二重积分二重积分是多元函数积分中最基础的一种形式。

它的计算方法依赖于重积分的定义以及二重积分的性质。

对于二重积分来说，我们需要将待求的函数转化为极坐标形式、直角坐标形式等，并确定积分区域的范围。

通过分割积分区域成为若干小块，再对每个小块进行积分求和，最后将所有小块的积分结果相加，可以得到二重积分的值。

在实际应用中，二重积分可以用来计算平面图形的面积、求解平面质心等问题。

二、三重积分与二重积分类似，三重积分是多元函数积分中的另一种形式。

三重积分的计算方法也依赖于重积分的定义以及三重积分的性质。

与二重积分不同的是，三重积分需要确定积分区域的范围，并将待求的函数转化为球坐标形式、柱坐标形式等。

同样地，通过分割积分区域成为若干小块，再对每个小块进行积分求和，最后将所有小块的积分结果相加，可以得到三重积分的值。

在实际应用中，三重积分可以用来计算空间图形的体积、质心等问题。

三、重积分的性质重积分具有一些重要的性质，这些性质对于计算积分结果以及简化计算过程都非常有帮助。

其中一些常见的性质包括积分线性性、积分对称性、积分的加法性和积分的估值性等。

积分线性性：对于常数a和b，函数f(x,y)和g(x,y)，有∬[D](af(x,y)+bg(x,y))dA = a∬[D]f(x,y)dA + b∬[D]g(x,y)dA。

这个性质使得我们在计算重积分时可以将积分区域分解成若干个子区域进行计算。

积分对称性：如果函数f(x,y)在区域D上关于x轴对称，则有∬[D]f(x,y)dA = 2∬[D1]f(x,y)dA，其中D1是区域D在x轴上方的部分。

类似地，还有关于y轴对称和原点对称的性质。

积分的加法性：对于两个不重叠的区域D1和D2，有∬[D1∪D2]f(x,y)dA = ∬[D1]f(x,y)dA + ∬[D2]f(x,y)dA。

多元函数积分学总结引言多元函数积分学是微积分的一个重要分支，研究的是多个变量的函数在特定区域上的积分计算和性质。

在实际问题中，我们经常需要求解多元函数的积分，以求得面积、体积、质量等物理量。

本文将对多元函数积分学的基本概念、计算方法和应用进行总结和介绍。

一、多元函数积分的基本概念1. 二重积分二重积分是多元函数积分学中最基本的概念之一。

它表示在二维平面上的一个有界区域上对函数进行积分。

二重积分的计算可以通过投影到坐标轴上的两个一元积分来实现。

根据积分区域的形状和函数性质的不同，二重积分可以分为类型I和类型II两种。

•类型I：积分区域为矩形、正方形或一般的可由直线分割成有限个矩形的区域。

•类型II：积分区域不属于类型I的情况，一般需要进行变量替换或极坐标转化来简化计算。

2. 三重积分三重积分是对三维空间内的函数进行积分。

它可以用于计算体积、质量、重心等与物体形状和密度有关的物理量。

三重积分的计算方法较为复杂，一般需要采用适当的坐标变换或者使用球坐标、柱坐标等不同坐标系下的积分公式来进行计算。

二、多元函数积分的计算方法1. Fubini定理Fubini定理是多元函数积分计算的基础定理之一。

它建立了二重积分和三重积分之间的关系，使得计算复杂多元函数积分时可以拆分为若干个简单的积分。

Fubini定理主要有两种形式：对于矩形区域上的二重积分，可以通过交换积分次序将其转化为两次一元积分。

对于空间区域上的三重积分，也可以利用类似的方法进行计算。

2. 极坐标和球坐标对于具有相关几何特性的问题，使用极坐标和球坐标可以简化多元函数积分的计算过程。

极坐标常用于计算平面上的二重积分，而球坐标常用于计算空间中的三重积分。

通过引入极坐标或球坐标的坐标变换，我们可以将原积分区域变换为一个更简单的形式，从而简化积分计算。

在实际应用中，灵活运用极坐标和球坐标可以大大提高计算效率。

三、多元函数积分的应用多元函数积分在物理学、工程学、经济学等领域有广泛的应用。

第十一章多元函数的积分学1. 计算下列二重积分：(1) ，；(2) ，；(3) ，；(4) ，．2 . 将二重积分化为不同顺序的累次积分：(1) 由轴与所围成；(2) 由及所围成；(3) 由和围成；(4) ．3 .改变下列累次积分的次序：(1) ；(2) ；(3) ．4 .设在所积分的区域上连续，证明．5. 计算下列二重积分：(1) ( ), 是由围成的区域；(2) 是由和围成的区域；(3) ：；(4) ：；(5) 由所围成；(6) 由所围成；(7) 是以和为顶点的三角形；(8) 由和所围成．6. 求下列二重积分：(1) ；(2) ；(3) ．7. 用极坐标变换将化为累次积分：(1) ：半圆；(2) ：半环；(3) ：圆；(4) ：正方形．8. 用极坐标变换计算下列二重积分：(1) ：；(2) 是圆的内部；(3) 由双纽线围成；(4) 由阿基米德螺线和半射线围成；(5) 由对数螺线和半射线围成．9. 在下列积分中引入新变量，将它们化为累次积分：(1) 若；(2) ( ) ，若；(3) ，其中＝，若；(4) ，其中＝( ) ，若．10 .作适当的变量代换，求下列积分：(1) 是由围成的区域；(2) 由围成；(3) 由围成．11 、利用二重积分求由下列曲面围成的立体的体积：(1) ；(2) ；(3) 球面与圆柱面（）的公共部分；(4) ( ) ；(6) ；(6) ．第十一章调用外部程序组件概览在ABAP/4 中，有多种使事务模块化的选项可供选择。

这些选项包括所有可以调用程序外部代码组件的方法。

这些外部组件可以是功能模块、其它事务、对话模块或报表。

内容嵌入程序调用.................................................................................................................................. １外部程序和滚动区 ..................................................................................................................... １外部程序和LUW 处理 ............................................................................................................... １调用功能模块.................................................................................................................................. ２访问功能库.................................................................................................................................. ２进行调用 ..................................................................................................................................... ２使用功能模块接口 ..................................................................................................................... ２处理例外情况 ............................................................................................................................ ３调用其它事务.................................................................................................................................. ４转到事务 ..................................................................................................................................... ４调用事务 ..................................................................................................................................... ４调用与调用程序共享SAP LUW 的事务 ................................................................................... ４调用对话模块.................................................................................................................................. ４运行时执行对话模块.................................................................................................................. ４用事务作为对话模块.................................................................................................................. ４提交报表........................................................................................................................................... ５向报表传送数据......................................................................................................................... ６保存或打印报表......................................................................................................................... ７在程序间传送数据........................................................................................................................... ７用SPA/GPA 参数传送数据...................................................................................................... ７详细信息，参见：嵌入程序调用(页１)调用功能模块(页２)调用其它事务(页４)调用对话模块(页４)提交报表(页５)在程序间传送数据(页７)嵌入程序调用外部程序组件由系统进行维护，对所有程序都可用。

多元函数积分学是数学的一个分支，它是对多元函数进行积分的理论。

与一元函数积分学相比，它更加复杂，但它为我们研究物理学、工程学和其他自然科学问题提供了更强大的工具。

在本文中，我将介绍的一些基本理论，包括重积分、极坐标变换、格林公式等。

一、重积分重积分是的基本概念，它是对多元函数在某一区域上的积分。

重积分可以表示为Riemann积分或Lebesgue积分两种形式，具体形式与多元函数的性质有关。

在Riemann积分中，我们将区域分成有限个小区域，对每个小区域内的多元函数进行积分，最后将积分结果相加。

而在Lebesgue积分中，我们采用测度的概念，将多元函数的定义域分成不可数个小区域，在每个小区域上定义一个测度，对多元函数在每个小区域内的值进行加权积分，最后求出所有小区域上的积分和即为整个区域上的积分。

重积分在物理学和工程学中有着广泛的应用，例如计算物体的体积、求解场的强度等。

同时，重积分也是进一步研究多元函数性质的基础。

二、极坐标变换极坐标变换是一种将平面直角坐标系上的点表示为极径和极角的变换。

它可以将一些复杂的函数转化为简单的极坐标函数，使得对多元函数进行积分更加方便。

在极坐标系中，被积函数可以表示为一个积分项和一个积分域，积分项为正态函数，积分域为从 $0$ 到 $2\pi$ 的一个闭区间和一个在某个圆内部的有界区域，在这个有界区域上的积分相当于在平面直角坐标系上的二重积分。

因此，我们可以使用积分转化公式将多元函数在极坐标系中的积分转化为在平面直角坐标系中的二重积分。

极坐标变换在数学中有着广泛的应用。

例如，对于一个椭球体积的计算，使用极坐标变换可以将三维积分转化为二维积分，更加方便计算。

三、格林公式格林公式是中的一个重要定理，它是关于多元函数的一个等式，用于计算曲面积分和线积分之间的关系。

在平面上，格林公式是一个计算平面上曲线积分和面积的公式，它表明二元函数在解析条件下，其在一个闭合路径内的曲线积分等于该函数在这个区域内的面积积分。

多元函数的积分在数学中，多元函数的积分是一个重要的概念和计算方法。

与一元函数的积分不同，多元函数的积分需要考虑多个自变量和相应的积分变量。

一、多元函数的积分定义对于二元函数f(x, y)，其在有界闭区域D上的积分可以定义为：∬f(x, y)dA = limΔx,Δy→0 Σf(xi, yj)ΔA其中，Δx和Δy分别表示x和y方向的分割长度，Σ表示对所有的(i, j)求和，xi和yj表示分割后的小区域的任意点，ΔA表示小区域的面积。

对于n元函数f(x1, x2, ..., xn)，其在有界闭区域D上的积分可以定义为：∭f(x1, x2, ..., xn)dV = limΔx1,Δx2,...,Δxn→0 Σf(x1i, x2j, ..., xnk)ΔV其中，Δx1, Δx2, ..., Δxn分别表示各个方向的分割长度，Σ表示对所有的(i1, i2, ..., in)求和，x1i, x2j, ..., xnk表示分割后小区域的任意点，ΔV表示小区域的体积。

二、多元函数的积分计算与一元函数的积分类似，对于多元函数的积分计算也需要借助于定积分的性质、微积分的基本定理和换元积分法等方法。

1. 球坐标和柱坐标对于具有某种对称性的多元函数，可以选择适当的坐标系来简化积分计算。

常用的坐标系有球坐标和柱坐标。

球坐标系适用于具有球对称性的问题，对于三元函数可以表示为：x = rsinθcosφ, y = rsinθsinφ, z = rcosθ其中，r代表点到坐标原点的距离，θ表示点与正z轴的夹角，φ表示点在xy平面上与正x轴的夹角。

柱坐标系适用于具有柱对称性的问题，对于三元函数可以表示为：x = rcosθ, y = rsinθ, z = z其中，r代表点到z轴的距离，θ表示点在xy平面上与正x轴的夹角，z表示点在z轴上的坐标。

2. 积分的性质多元函数的积分具有类似于一元函数积分的一些性质，如线性性质、可加性质、保号性质等。

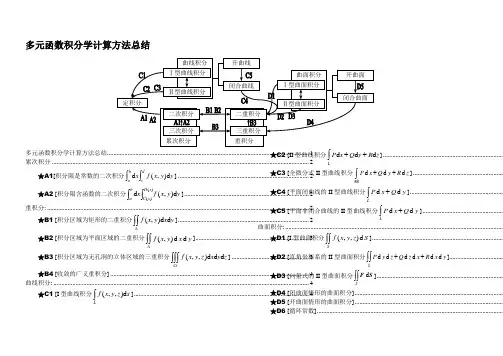
多元函数积分学计算方法总结多元函数积分学计算方法总结 ................................................................................................................................ 1 累次积分 ................................................................................................................................................................... 2 ★A1[积分限是常数的二次积分⎰⎰dcbay y x f x d ),(d ] ................................................................................... 2 ★A2 [积分限含函数的二次积分⎰⎰)()(d ),(d x D x C bay y x f x ] ...............................................................................2 重积分: ...................................................................................................................................................................... 2 ★B1 [积分区域为矩形的二重积分⎰⎰Λy x y x f d d ),(] (2)★B2 [积分区域为平面区域的二重积分(,)d d f x y x y Λ⎰⎰] ........................................................................3 ★B3 [积分区域为无孔洞的立体区域的三重积分⎰⎰⎰Ωz y x z y x f d d d ),,(] .................................................3 ★B4 [收敛的广义重积分] .............................................................................................................................. 4 曲线积分: (4)★C1 [I 型曲线积分⎰Ls z y x f d ),,(] ...............................................................................................................4 ★C2 [II 型曲线积分⎰++Lz R y Q x P d d d ] ............................................................................★C3 [全微分式II 型曲线积分d d d ABP x Q y R z ++⎰] .........................................................★C4 [平面闭曲线的II 型曲线积分d d LP x Q y +⎰] ...........................................................★C5 [平面非闭合曲线的II 型曲线积分d d L P x Q y +⎰] ...................................................曲面积分: ..........................................................................................................................................★D1 [I 型曲面积分(,,)d Sf x y z S ⎰⎰] ...................................................................................★D2 [直角坐标系的II 型曲面积分d d d d d d SP y z Q z x R x y ++⎰⎰]..................................★D3 [向量式的II 型曲面积分d S⎰⎰F S ] ................................................................................★D4 [闭曲面情形的曲面积分] ..............................................................................................★D5 [开曲面情形的曲面积分] ..............................................................................................★D6 [循环常数] ......................................................................................................................约定:a ,b ,c ,d 为已知常数, ,,,αβγδ是已知的弧度, ,,x y z 是原空间直角坐标系分量, ,,u v w 是新变量同时也是变量代换函数记号, ,,ρθφ是球坐标\极坐标\柱坐标系的分量,(),(),(),()A B C D ⋅⋅⋅⋅是积分限函数, (),(),()f g h ⋅⋅⋅表示积分函数, ω表示现有变量的全微分, (),(),()P Q R ⋅⋅⋅是场向量函数F 的分量,均为(,,)x y z 的函数.L 表示空间曲线,Λ表示空间曲面,Ω表示空间区域,∂表示取上述区域的边界或变量的偏微分. Γ是带方向的曲线, S 是带方向的曲面区域, S (黑斜体)是法向量或者说曲面积分元.累次积分二次积分⎰⎰bad cx y y x f d )d ),((也写作⎰⎰d cb ay y x f x d ),(d ;三次积分z z y x f y x pqd c b a d ),,(d d ⎰⎰⎰★A1[积分限是常数的二次积分⎰⎰dcb ay y x f x d ),(d ]求法: ⎰dcy y x f d ),(先求,把x 当作常数,只对y 求原函数并求出积分值g (x )(可能和x 无关).然后将它作为新的被积函数,也就是计算⎰bax x g d )(，即可得到累次积分的积分值.result x x g y y x f x bad cba==⎰⎰⎰d )(d ),(d性质:①分量积分顺序改变,积分值不变;①⎰⎰⎰⎰=b a d c d c b a x y x f y y y x f x d ),(d d ),(d ; ②分离分量因子后分别积分的乘积等于原积分值; ②)d )(()d )((d )()(d ⎰⎰⎰⎰⋅=⋅d c b a d c b a y y g x x f y y g x f x ③被积函数可加性.③⎰⎰⎰⎰⎰⎰+=+dcbadcbadcbay y x g x y y x f x y y x g y x f x d ),(d d ),(d d )),(),((d★A2 [积分限含函数的二次积分⎰⎰)()(d ),(d x D x C b ay y x f x ]求法:先将x 看成常数,求出f 关于y 的原函数g (y )(可能含有x );再将))(())((x C g x D g -作为关于x 的新的被积函数;最后算出定积分的值.⎰⎰⎰=-=bax D x C baresult x x C g x D g y y x f x d )))(())(((d ),(d )()(重积分:二重积分⎰⎰Λy x y x f d d ),(;三重积分⎰⎰⎰Ωz y x z y x f d d d ),,(★B1 [积分区域为矩形的二重积分⎰⎰Λy x y x f d d ),(]求法:把积分区域Λ的矩形化为区间的乘积的形式[a ,b ]×[c ,d ],被积函数不变,区间端点按分量顺序作为二次积分的积分限.积分区域为长方体的三重积分求法类似.],[],[,...d ),(d d d ),(d c b a result y y x f x y x y x f dcb a⨯=Λ===⎰⎰⎰⎰Λ★B2 [积分区域为平面区域的二重积分(,)d d f x y x y Λ⎰⎰]求法:定下分量的积分顺序,如先y 后x ,那么先写出Λ中所有点的x 分量的最小值a ,最大值b ,以取得上述最值的点为端点,将Λ的边界分成下半边界C (x )和上半边界D (x ).那么可以化为被积函数不变,先对积分区间为从C (x )到D (x )的y 分量积分,再对积分区间为[a ,b ]的x 分量积分的二次积分.积分区域为无孔洞的立体区域的三重积分也有类似的方法.)]}(),([],,[|),{(,...d ),(d d d ),()()(x D x C y b a x y x result y y x f x y x y x f x D x C b a ∈∈=Λ===⎰⎰⎰⎰Λ)]},(),,([)],(),([],,[|),{(,d ),,(d d d d d ),,()()(),(),(y x D y x C z x B x A y b a x y x z z y x f y x z y x z y x f x B x A y x D y x C ba∈∈∈=Ω=⎰⎰⎰⎰⎰⎰Ω性质:①变量代换后积分值不变; (,)(,)d d ((,),(,))d d ,(,)x y f x y x y f u x y v x y u v u v ΛΛ∂=⋅∂⎰⎰⎰⎰①(,),(,)det (,),(,)u vu v x x u u x y x y y y v v x y u v ''=⎛⎫⎧∂=⎨⎪''=∂⎩⎝⎭变换为,.ΛΛ是由的不等式根据变量代换改写并加上新变量的限制如极坐标变换cos ,sin ,x y ρθρθ=⎧⎨=⎩故有新的限制0,||ρθπ≥≤(,)d d ((,),(,))d d f x y x y f x y x y ρθρρθΛΛ=⋅⎰⎰⎰⎰;球坐标变换cos cos ,sin cos ,sin ,x y z ρθϕρθϕρϕ=⎧⎪=⎨⎪=⎩故有新限制0,,2πρθπϕ≥≤≤,(,,)d d d ((),(),())cos d d d f x y z x y z f ρθϕρϕρθϕΩΩ=⋅⋅⋅⋅⎰⎰⎰⎰⎰⎰.②积分值与积分顺序无关,但对应的累次积分不同;②()d ()()()(,)d d d (,)d d (,)d ,b D x B x a C x c A x f x y x y x f x y y y f x y x Λ==⎰⎰⎰⎰⎰⎰{(,)|[,],[(),()]}{(,)|[,d],[(),()]}x y x a b y C x D x x y y c x A y B y Λ=∈∈=∈∈ ③零函数或零测度集Λ上的重积分必为零.③三重积分的积分区域若是面、线、点,则积分值为零,二重积分的积分区域是线、点时,积分值为零.★B3 [积分区域为无孔洞的立体区域的三重积分⎰⎰⎰Ωz y x z y x f d d d ),,(]求法:定下分量的积分顺序,如先(y ,z )后x ,那么先解出Ω的不等式(组)关于g (y ,z )的解)](),([x B x A ,即有平面区域Λ.继而有被积函数不变,视x 为常数,关于(y ,z )的二重积分,随后做关于x 分量的第二次积分.类似的积分顺序也可以是先(x , y )后z .}),(],,[|),,{()]},(),([),(|),{(,d )(d d ),,(d d d d ),,(Λ∈∈=Ω∈=Λ===⎰⎰⎰⎰⎰⎰⎰ΛΩz y b a x z y x x B x A z y g z y result x x h z y z y x f x z y x z y x f bab a★B4 [收敛的广义重积分]求法:只要广义重积分是收敛的,就可以按照一般重积分的求法求得收敛值.曲线积分:Ⅰ型曲线积分⎰Ls z y x f d ),,(;Ⅱ型曲线积分⎰++Lz R y Q x P d d d★C1 [I 型曲线积分⎰Ls z y x f d ),,(]求法:首要任务是将积分曲线L 的方程参数化,用参数t 表示,并且表示出积分区间.将参数方程代入被积函数,弧微分d s 按公式计算即可得到定积分.(,,)d ((),(),(,{(,,)|(),(),(),[,]}baLf x y z s f x t y t z t t result L x y z x x t y y t z z t t a b ======∈⎰⎰★C2 [II 型曲线积分⎰++Lz R y Q x P d d d ]求法:将积分曲线L 的方程参数化,用参数t 表示,并且表示出积分区间.函数P ,Q ,R 中的变量换为t 后乘上对应分量关于t 的导数作为新的被积函数,做关于t 的积分.但注意这里的曲线是有向的,右手法则下逆时针取正,顺时针取负.()d d d ()()()d ,{(),(),()},:bt t t aLP x Q y R z P t x Q t y R t z t result L x t y t z t t a b '''++=±⋅+⋅+⋅==→⎰⎰★C3 [全微分式II 型曲线积分d d d ABP x Q y R z ++⎰]求法:若P Q y x ∂∂=∂∂(二元), P R z x∂∂=∂∂,且Q R z y ∂∂=∂∂则该空间曲线微分是全微分式(恰当)的.对微分形式凑微分得到原函数F ,再代入积分区间即可得结果.注意这里曲线也是有方向的.d d d d (,,)(,,),d d d d BBA AABP x Q y R z F x y z F x y z result F P x Q y R z ++=±=±==++⎰⎰其中★C4 [平面闭曲线的II 型曲线积分d d LP x Q y +⎰]求法:对场向量的分量函数P ,Q 求全微分,形如d d d P PP x y x y∂∂=+∂∂,并与原对应分量取外微分,作为二重积分的微分形式.二重积分的区域是以L 为边界的曲面.d d (d )d (d )d d d (,)d d ...,L P Q P x Q y P x Q y x y f x y x y result L y x ΛΛΛ⎛⎫∂∂+=∧+∧=-+====∂Λ ⎪∂∂⎝⎭⎰⎰⎰⎰⎰⎰⎰ ★C5 [平面非闭合曲线的II 型曲线积分d d LP x Q y +⎰]求法:补上一条连接端点的线段AB ,然后以L AB ⋃作为闭曲线化为二重积分,并加上的反方向的AB 的曲线积分.d d ()(d d )(,)d d d d ...,AABBLL ABP x Q y P x Q y f x y x y P x Q y result L AB Λ⋃+=++=++==⋃=∂Λ⎰⎰⎰⎰⎰⎰性质:①被积函数曲面与区域公用对称轴/对称面时,前者在后者两侧(奇),则积分值为零,前者在后者的同侧(偶),则积分值等于积分区域取一半的积分值的两倍.②函数中的分量交换后函数相似的,积分值相等.曲面积分:Ⅰ型曲面积分(,,)d Sf x y z S ⎰⎰;Ⅱ型曲面积分:直角坐标式d d d d d d S P y z Q z x R x y ++⎰⎰;向量式d S⎰⎰F S★D1 [I 型曲面积分(,,)d Sf x y z S ⎰⎰]求法:先针对S 求出参数方程,分别对曲面向量求关于某两个变量的偏导向量函数(可以是原来的变量,也可以代换成其他变量),然后取这两者的外积的模,便可以得到普通的二重积分.(,){(,),(,),(,)},(,){,,},{,,}(,,)d ((,),(,),(,))d d ...u v uv SDS r u v x u v y u v z u v u v Dx y z x y z r r u u u v v vf x y z S f x u v y u v z u v r r u v result≡=∈∂∂∂∂∂∂''==∂∂∂∂∂∂''=⋅⨯==⎰⎰⎰⎰性质:当S 为变量的隐式时,替换成其中两个变量时,法向量模可以用偏导的模来取代. ★D2 [直角坐标系的II 型曲面积分d d d d d d SP y z Q z x R x y ++⎰⎰]求法: 这种方法是将三部分分开计算的.若积分曲面是闭合的,且积分方向是曲面的内侧或外侧,则先将曲面合理分割.再确定曲面积分方向和曲面投影方向的关系,如计算d d SP y z ⎰⎰的时候,若yz D 是S 从x 轴负方向投向yOz 面的投影,且积分方向是向x 轴正方向,则定积分取正号.接下来确定投影区域D ,将S 的关于x (或y 或z )的显式并代入P (或Q 或R )中作为新的被积函数.(II)d d ((,),,)d d ...yzSD P y z P x y z y z y z result =±==⎰⎰⎰⎰★D3 [向量式的II 型曲面积分d S⎰⎰F S ]求法: 先针对S 求出参数方程,分别对曲面向量求关于某两个变量的偏导向量函数(可以是原来的变量,也可以代换成其他变量),然后取这两者的外积(即关于曲面S 上得每一点的法向量函数).将它和场向量{,,}P Q R =F 取内积作为新区域D 下的二重积分的被积函数.d {,,}()d d ...uv SDP Q R r r u v result ''=⋅⨯==⎰⎰⎰⎰F S★D4 [闭曲面情形的曲面积分] 求法:★D5 [开曲面情形的曲面积分] 求法:★D6 [循环常数] 求法:。

多元函数积分学多元函数积分学是一门研究多元函数及其应用的数学分支。

这门学科涉及多变量函数的积分、定积分、无穷积分以及分析在多变量函数上的积分问题。

在多元函数积分学中，多元函数的定义以及它们的性质是基本的。

它们可以在任何给定的多元函数空间中定义，是多元函数积分学的基本概念和研究的重要内容。

多元函数积分学的主要任务是研究多变量函数的积分问题。

在多元函数积分学中，多变量函数积分可以分为定积分和无穷积分两类。

定积分是指在给定积分问题的多变量函数中求解积分，它一般包括一元函数积分、二元函数积分、多变量函数的积分和曲线的积分等。

它可以使用多种方法求解，比如高斯积分、梯形积分、拉斯维加斯积分以及蒙特卡罗积分等。

而无穷积分则是指在多变量函数中对积分域上的数学函数进行积分，它可以使用泰勒级数展开、拉普拉斯变换、拉格朗日变换等进行求解。

多变量函数积分与一元函数积分也有不同之处。

一元函数积分是指积分域上的一元函数，这是一种非常直观的概念，我们可以使用经典的定积分方法来解决一元函数的积分问题。

而多变量函数积分则不同，因为它需要考虑多变量函数的复杂性，在求解多变量函数积分时，我们需要考虑几何图形及其各种变换，这为求解多变量函数积分提出了新的问题。

另外，多变量函数积分学还涉及空间几何的概念，它的主要任务是研究多变量函数的空间性质，比如曲面的概念、曲面的法线、曲线的曲率等。

这些涉及空间几何的概念，可以帮助我们更深入地理解多元函数的积分过程，从而更加深入地研究多元函数积分的性质和特性。

多元函数积分学的研究主要是为了理解多变量函数的性质和特征，从而使用多元函数更好地描述现实中的现象和事物。

它也为研究多变量函数的更复杂的应用如无限维空间函数提供基础，比如用多元函数积分来研究抽象代数结构，研究计算机图形学相关的概念等。

因此，多元函数积分学是一门重要的学科，它是理解多元函数的性质和特征的基础。

它不仅为许多应用提供了理论依据，而且还可以帮助我们更深入地理解多元函数的性质和特征，从而更加深入地研究多元函数的积分和抽象代数结构。