当前位置：文档之家 › 传热学7第七章

传热学7第七章

  • 格式：doc
  • 大小：401.00 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

(完整版)《传热学》第7章_相变对流传热

(完整版)《传热学》第7章_相变对流传热
1. 产生原因不同（液体与壁面浸润程度） 2. 换热强度不同 3. 珠状凝结不持久，工程中主要采用膜状凝结作为设计依据。
5
第7章 相变对流传热
7.2 膜状凝结分析解及计算关联式
7.2.1 努塞尔的蒸气层流膜状凝结分析解(温度、传热系数及动量分布)
1. 对实际问题的简化假设
努塞尔的分析是对纯净的饱和蒸气在均匀壁温的竖直表面上的层流
x
1/
4
整个竖壁上的温差ts-tw为常数，因此，整个
竖壁的平均表面传热系数为：
hV
1 l
l 0
hx dx
34hxl
0.943lgl rts 3ltl2w
1/ 4
液膜层流时竖壁膜状凝结的努塞尔理论解，
如果有倾角φ的话，直接改为gsin φ即可。
8
第7章 相变对流传热
7.2.2 竖直管与水平管的比较及实验验证
第7章 相变对流传热
7.1 凝结传热的模式 7.2 膜状凝结分析解及计算关联式 7.3 膜状凝结的影响因素及其传热
强化 7.4 沸腾传热的模式 7.5 大容器沸腾传热的实验关联式 7.6 沸腾传热的影响因素及强化 7.7 热管简介
1
第7章 相变对流传热
引入：
对流传热
强制对流传热 自然对流传热 无相变
膜状凝结的热阻通常比珠状凝结大一个数量级以上，
膜状凝结的表面传热系数的数量级为“成千上万”，而
珠状凝结的表面传热系数可以高达几十万！
g
tw ts
tw ts
4
第7章 相变对流传热
珠状凝结的关键问题是在常规金属表面上难 以产生与维持！！ 7.1.3 膜状凝结是工程设计的依据 常用蒸气在洁净的条件下都能得到膜状凝结。 实现起来较容易且计算简单，因此，采用膜状 凝结的计算式作为设计的依据。 强化传热的主要途径是减薄液膜的厚度！！！ 珠状和膜状凝结的异同：

《传热学》第7章-凝结与沸腾换热

《传热学》第7章-凝结与沸腾换热

补充例题3
v 思路： 膜态沸腾换热套用公式计算即可。
稳定的膜态沸腾时，金属丝的电流的发热量 一部分通过沸腾换热传给了水，其余部分则 使金属丝的内能增加（温度升高），这是一 个能量平衡。
补充例题3
v 解：膜态沸腾换热系数的计算套教材中的公式，略 去。结果为： h=236.70 W/(m2.℃)
每米长金属丝的传热量为:
理论解的修正
h
=
0.943

gγρ
µH (ts
2λ3 − tw
1/ 4
)
实验证实： Re < 20
时，实验结果与理论解相吻合
Re > 20 时，实验结果比理论解高20%
所以在工程计算时将该式的系数加大20%
h
=
1.13

gγρ 2λ3
µl(ts − tw
)
1/
4
定性温度
tm
传热学
第7章 凝结与沸腾换热 Condensation and boiling
简介
蒸气被冷却凝结成液体的换热过程称为凝结换热； 液体被加热沸腾变成蒸气的换热过程称为沸腾换热
——有相变的对流换热
一般情况下，凝结和沸腾换热的表面传热系数要比单相 流体的对流换热高出几倍甚至几十倍。
7-1 凝结换热现象
膜状凝结换热 的主要阻力
=
1 2
(ts
+
tw
)
其他
单根水平圆管外壁面上的层流膜状凝结换热平均表面传热系数
h=
( ) 紊流膜状凝结换热
0.729

gγρ µd ts
2λ3 − tw
1/ 4
( ) 整个垂直壁面的平均表面传热系数

传热学第7章汇总

传热学第7章汇总

0
积分两次，并将边界条件代入，得到液膜内温度分布： t tw
ts tw
y
3.液膜微元段热平衡：
MH ——凝液带入热量
M dM dx H ——凝液带出热量
dx
H dM ——蒸气带入热量
t y
w
dx——墙壁导热出热量
H ——凝液焓（饱和液体）
H ——蒸气焓（饱和气体）
M ——凝液质流量
蒸气含不凝气体
影 响
膜层表面蒸气分压降低，ts降低，ts -tw降低
因 素
低Rec→凝液积聚，液膜增厚→h减小
表面粗糙度
高Rec→凸出点对凝液产生扰动→h增大
蒸气含油→壁上形成油垢→ h减小
h减小
过热蒸气→蒸气与凝液焓差增大→ h增大（计算时潜热修正为实际焓差）
增强凝结换热的措施：
1.改变表面几何特征： 采用各种带有尖峰的表面， 使在其上冷凝的液膜拉薄， 或者使已凝结的液体尽快 从换热表面上排泄掉
0.943
lts
tw
定性温度：ts tw 2
定型尺寸：x(l)
注意点：以上两式并非最后的正确结果，计算中不得直接使用！
水平圆管层流膜状凝结换热平均表面传热系数：
2 g3r
14
h
0.725
d
ts
tw
定性温度：ts tw 2
定型尺寸：d
将平均表面传热系数表达式写为准则方程：
垂直壁：
Co
1.47
v为蒸汽密度
假定液膜流动缓慢，则惯性力项可忽略，动量方程可简化为：
d 2u dy 2
v
g
0
一般情况下： v 从而： v
积分两次，得到液膜内速度分布：

传热学第七章

传热学第七章
: 频率 : 波长
C : 电磁波传播速度
在真空中，C 3 108 m / s 在大气中，略低于此值
第七章 辐射传热
第一节 基本概念 一、热辐射的本质
3、波长范围（如图7-1所示）
图7-1 电磁波谱
第七章 辐射传热
第一节 基本概念 一、热辐射的本质
3、波长范围（如图7-1所示）
（1）热辐射产生的电磁波称为热射线。从理论上讲，其波长 包括整个电磁波谱，即波长从零到无穷大。 （2）实用中，通常把波长在0.1～100μm范围内的电磁波称为 热射线。它包括部分紫外线、全部可见光和部分红外线： ①部分紫外线（0.1～0.38μm） 热射线（0.1～100μm） ②全部可见光（0.38～0.76μm） ③部分红外线（0.76～100μm）
第七章 辐射传热
第一节 基本概念 五、黑体、白体和透明体
1、理想模型 （1）把吸收比α=1的物体称为绝对黑体，简称黑体。 （2）把反射比ρ=1的物体称为绝对白体，简称白体。
（3）把透射比σ=1的物体称为绝对透明体，简称透明体
※ 黑体、白体、透明体都是理想模型，
是理论研究的基础，自然界中并不存在。
第七章 辐射传热
第七章 辐射传热
第二节 黑体辐射的基本定律 二、普朗克定律
⑤当黑体的T＞800K时，其辐射能中才明显地具有波长为 0.38～0.76μm的可见光射线。
※随着温度的升高，可见光射线增加。
※当温度达到5800K时，Ebλ的峰值才位于可见光范围。 ※太阳可近似认为是表面温度为5800K的黑体，根据计算，
图7-3 物体表面的反射 a)镜面反射；b）漫反射
第七章 辐射传热
第一节 基本概念 四、漫射表面
1、当物体表面较光滑，其粗糙不平的尺度小于热射线的波长时， 物体表面对投射辐射呈镜面反射，入射角等于反射角，该表 面称为镜面，如图7-3a)所示。 2、当物体表面粗糙不平的尺度大于热射线的波长时，物体表面 对投射辐射呈漫反射，其吸收比大于镜面，该表面称为漫反 射表面，如图7-3b)所示。 ※一般工程材料的表面均可近似作为漫反射表面。 3、若漫反射表面同时能向周围半球空间均匀发射辐射能，则称 该表面为漫射表面。

第七章凝结及沸腾换热_传热学

第七章凝结及沸腾换热_传热学

23
3 大空间饱和沸腾曲线：
表征了大容器饱和沸腾的全部过程，共包括4个换热规律不 同的阶段：自然对流、泡态沸腾、过渡沸腾和稳定膜态沸腾， 如图所示：
qmax
qmin
24
4.几点说明： （1）上述热流密度的峰值qmax 有重大意义，称为临界 热流密度，亦称烧毁点。一般用核态沸腾转折点DNB作 为监视接近qmax的警戒。这一点对热流密度可控和温度 可控的两种情况都非常重要。 （2）对稳定膜态沸腾，因为热量必须穿过的是热阻较 大的汽膜，所以换热系数比凝结小得多。
25
三. 大空间泡态沸腾表面传热系数计算
沸腾换热也是对流换热的一种，因此，牛顿冷却公式仍 然适用，即
q h(tw ts ) ht
但对于沸腾换热的h却又许多不同的计算公式 影响泡态沸腾的因素主要是过热度和汽化核心数，而汽 化核心数受表面材料、表面状况、压力等因素的支配，所 以沸腾换热的情况液比较复杂，导致了个计算公式分歧较 大。目前存在两种计算是，一种是针对某一种液体，另一 种是广泛适用于各种液体的。
与膜状凝结换热不同，液体中的不凝结气体会使沸腾换热 得到某种程度的强化 2 过冷度
只影响过冷沸腾，不影响饱和沸腾，因自然对流换热时，
h (tw， 因t f 此)n ，过冷会强化换热。
30
3.液位高度
当传热表面上的液位足够高时， 沸腾换热表面传热系数与液位 高度无关。但当液位降低到一 定值时，表面传热系数会明显 地随液 位的降低而升高(临界 液位)。
2t y 2
5
考虑（3）液膜的惯性力忽略
l (u
u x
v
u y
)
0
考虑（7）忽略蒸汽密度
dp 0 dx
考虑（5） 膜内温度线性分布， 即热量转移只有导热

传热学-第七章

传热学-第七章
忽略蒸汽密度；(8)液膜表面平整无波动
边界层微分方程组：
u v 0 x y u u dp 2u v ) l g l 2 l (u x y dx y 2 t t t u v al 2 y y x
xc xc h hl ht 1 l l
式中：hl 为层流段的传热系数； ht 为湍流段的传热系数；xc 为层流转变为湍流时转折点的高度； l 为竖壁的总高度
利用上面思想，整理的实验关联式：
1 3
Nu 58 P r s
1 2
Ga Re
3 Pr w 4 9200 Re 253 Pr s 1 4
式中： Nu=hl/ ； Ga=gl3/2 。除 Prw 用壁温 tw 计算外，其余
物理量的定性温度均为ts。
例 1 ：饱和水蒸汽在高度 L=1.5m 的竖管外表面上做层流膜状凝
结。水蒸汽压力为 p=2.5×105Pa ，管子表面温度为 123℃ 。试 计算离开管顶为 0.1m 、 0.2m 、 0.4m 、 0.6m 及 1.0m 处液膜厚度 和局部表面传热系数。 解：根据饱和水蒸汽层流膜状凝结的分析解可知 液膜厚度
对于倾斜壁，则用 gsin 代替以上各式中的 g 即可。另 外，除了对波动的修正外，其他假设也有人做了相关的研究， 如：当Pr≈1，并且
r Ja 1 c p (t s t w )
时，惯性力项和液膜过冷度的影响均可忽略。
(4) 水平圆管 努塞尔的理论分析可推广到水平圆管及球表面上的层流 膜状凝结
第七章
流换热和自然对流换热
相变对流传热
第五、六章我们分析了无相变的对流换热，包括强制对

传热学第七章

传热学第七章

7. 单相流体对流换热及其实验关联式7.1 知识结构1. 实验关联式应用条件：适用范围，定性温度，特征尺度，特征流速，修正系数（入口、弯道、特性）。

2. 常用实验关联式：管内强制对流（紊流、层流及过渡流）（非圆形管道的当量直径计算）； 外掠（平板、单管、管束）强制对流； 自然对流（大空间、有限空间）。

7.2 重点内容剖析由于对流换热问题的复杂性，大多数工程问题不能依靠分析解，而是依靠相似理论指导下的实验解。

在应用实验关联式（准则方程）时要注意以下几个方面：（1） 实验范围（已定准则范围）内的相似现象一般不能外推； （2） 注意关联式所规定的定性温度、特征尺度、特征流速； （3） 正确选用各种修正系数(物性，入口，弯管……)7.2.1 强制对流换热及其实验关联式 一、管槽内强制对流换热特征 1．流动状态Re ：0 2300 10000层流 过渡流 湍流 2．速度分布温度对流速分布的影响是通过粘性作用的。

液体粘性随温度升高而降低，气体粘性随温度升高而增加。

相同切应力作用下，粘度越大，速度在壁面法线方向的变化率越小。

3．典型边界条件恒热流：边界处热流密度恒定不变，如电加热器。

恒壁温：边界处温度恒定不变，如冷凝器。

湍流时（除液态金属外）两种边界条件对传热系数的影响可忽略不计，但对层流和低Pr 介质，两种边界条件下传热系数的差别不容忽视。

4．原则性准则方程()Pr Re,f Nu = (7-1)5．入口效应：入口段：从入口至流动边界层在管道中心汇合处。

层流入口段长径比(比湍流大)：Pr Re 05.0≈d l 湍流入口段长径比：60<d l 充分发展段：流动边界汇合处下游。

入口效应：由于入口段边界层较薄，平均表面传热系数比充分发展段大，入口段有强化传热的作用。

(短管强化传热)6．努塞尔特准则的物性修正系数： (温度场不均匀→物性场不均匀)nw f nwf nwf T T ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛Pr Pr ,,ηη下标：f ——流体温度下参数w ——壁面温度下参数二、管内湍流换热实验关联式nf ff Nu Pr Re 023.08.0= (7-2)加热液体时：n=0.4 冷却液体时：n=0.3定性温度：流体平均温度（管道进出口平均温度）特性尺度：管道内径(由关联式分析可知：h~d -0.2 →小管强化传热) 适用范围：Ref=104~1.2⨯105，Prf=0.7~120，l/d>60， 对于短管或弯管：乘以相应修正系数对于非圆形管道：用当量直径代替管道直径气体：不超过50 ℃ 传热温差 水：不超过30 ℃ 油：不超过10 ℃温差超出范围时，参考文献[1]P165有推荐公式和使用条件 注：① 非圆形管道(当量直径)：UAde d 4== (7-3) A ——流动截面积 U ——湿周长② 入口效应修正系数（l/d<60）7.01⎪⎭⎫⎝⎛+=l d c l (7-4)③ 弯管修正（二次环流强化传热）(弯管强化传热)对于气体Rdc r 77.11+= (7-5) R 为弯道半径（曲率半径）对于液体33.101⎪⎭⎫⎝⎛+=R d c r (7-6)三、管内层流换热实验关联式(层流充分发展段) 对于恒热流边界条件：36.4=Nu 对于恒壁温边界条件：66.3=Nu(对于非圆形管道参见参考文献[1]P168~169表5-3、4) 管内层流换热实验关联式的应用要注意以下几点： (1) 对于同一截面形状的通道，恒热流Nu>恒壁温Nu(2) 等截面直通道内的层流充分发展段Nu 与Re 无关(自模化)(3) 对于层流，当量直径只是一几何参数，不能用它来统一不同截面通道的换热和阻力计算表达式。

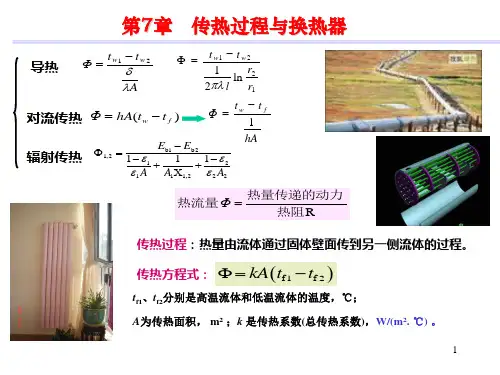
传热学-第7章 传热过程的分析和计算2

传热学-第7章 传热过程的分析和计算2
13
四、强化传热的考虑
kAtf1 tf 2
• 为强化传热，有三条途径：
★方法1：提高温差 ★方法2：提高传热系数
14
★如何提高传热系数？
k
1 h1
1 h2
1
1 h1
1 h2
1
数学上可以证明
k min( h1, h2 )
提高较小的表面传热系数值，强化薄弱环节，效果最好
15
• h1＝1000，h2＝10，没有强化前：k=9.90 W/(m2.K)
t m in
Δtmax、Δtmin 均指端差，即同一端热流体与冷流体间的温差。 Δtmax 是其中大温差， Δtmin 则是其中小温差。
26
平均温差的另一种更为简单的形式是算术平均温差，即
tm,算术
tmax
2
tmin
tm,对数
t max tmin ln t max
t m in
t1' t1"
t
' 2
温差 t f 1 沿t f 2整 个壁面不是常数，必须采用整个面积上的平均温差
t m
kAtm
25
（一）简单顺流及逆流换热器的对数平均温差
t1'
t1"
t1'
t
' 2
t
" 2
t
" 2
t1"
t
' 2
顺流
逆流
换热器中流体温度沿程变化的示意图
可以推导出顺流和逆流的平均温差公式为
对数平均温差
tm
t max tmin ln t max
第7章 传热过程与换热器
导热
Φ

传热学课件-第七章 相变对流传热精品文档71页

传热学课件-第七章 相变对流传热精品文档71页

对于Pr数接近于1或大于1的流体，只要
r
1
c p (ts tw )
惯性力项及液膜过冷度的影响均可略而不计。
实验表明，液膜由层流转变为湍流的临界雷诺数为 1600。
三、湍流膜状凝结传热
凝结液体流动也分层流和湍流，并且其判断依据 仍然时Re，
Re deul
式中：
ul 为 x = l 处液膜层的平均流速；
ρ=958.4kg/m3,μ=2.825 ×104则kg有/(：m.sh),λ=1.01.638WlrL/g((tms3l .Kl2t)w)1/4
1 .1 3 9 .8 2 .8 22 2 1 5 5 0 4 1 7 0 3 0 .3 9 (1 8 .4 2 0 5 9 0 0 .6 )8 3 8 1 /4
hhl
xc l
ht
1xlc
式中：hl为层流段的传热系数；ht为湍流段的传热系数； xc为层流转变为湍流时转折点的高度
l为竖壁的总高度
实验关联式：
N uG a1/3
R e
1/4
58P rs1/2 P P r rw s (R e3/4253)9200
式中：Nuhl/;Gagl3 /2 。除 P r w 用壁温 t w
u
t x
v
t y
0
只有u 和 t 两个未知量，不需要补充连续性方程 可以求解。于是，上面得方程组化简为：
l
g
l
2u y 2
0
a
l
2t y 2
0
边界条件：
y0时，u0, t tw
y时，du 0,
dy
t ts
3.主要求解过程及结果
求解上面方程可得：
（1）

传热学 第7章-热辐射的基本定律

传热学 第7章-热辐射的基本定律

第七章热辐射的基本定律在工程技术中，在日常生活中，辐射换热现象是屡见不鲜的。

太阳对大地的照射是最常见的辐射现象。

高炉中灼热的火焰会烘烤得人们难以忍受‘太阳对人造卫星的辐射，会使卫星的朝阳面的温度明显地高于卫星背阳面的温度；高温发动机部件与飞机机体之间的辐射换热严重地影响着飞机的结构与强度设计，等等。

特别是近年来，人类对太阳能的利用，都大大地促进了人们对辐射换热的研究。

本章首先介绍辐射的基本特性和基本规律；然后重点讨论物体之间的辐射换热规律；最后对气体辐射换热的特点作扼要的介绍。

第一节基本概念1－1 热辐射的本质和特征由于不同的原因，物体能够向其所在的空间发射各种不同波长的电磁波；不同波长的电磁波具有不同的效应，人们可以利用不同波长的电磁波效应达到一定的目的。

比如，人们可以利用无线电波传送信息，利用x射线穿透物质的能力进行零件探伤，利用热射线传递热能，等等。

人们根据电磁波不同效应把电磁波分成若干波段。

波长λ＝0.38一0.76μm的电磁波段称为可见光波段λ＝0.76—1000 μm的电磁波段称为红外波段(一般将红外波段范围又分为近红外波段和远红外波段，近红外波段为λ＝0.7—25μm，远红外波段为λ＝25—1000μm)；波长大于1000μm的电磁波段称为无线电波段(根据其波长的不同又可分为雷达、视频和广播三个波段)；波长小于0.4μm的电磁波依次分为紫外线、x射线和Y射线等。

可见光和红外线以及紫外线的一部分被物体吸收后产生热效应，即波长λ＝0.1—1000 μm范围内的电磁技能被物体吸收变为热能，因此，这一波长范围的电磁波称为热射线。

因为在一般常见的工业温度条件下，其辐射波长均在这一范围，所以本课程所感兴趣的将是热射线，下面将专门讨论这一波长范围内电磁波的发射、传播和吸收的规律。

一、热辐射的本质和特点1、发射辐射能是各类物质的固有特性。

当原子内部的电子受温和振动时，产生交替变化的电场和磁场，发出电磁波向空间传播，这就是辐射。

工程热力学与传热学第7章气体的流动.

工程热力学与传热学第7章气体的流动.

第七章 气体的流动(Gas Flow)第一节 气体在喷管和扩压管中的流动主题1：喷管和扩压管的断面变化规律一、稳定流动基本方程气体在喷管和扩压管中的流动过程作可逆绝热过程，气体流动过程所依据的基本方程式有：连续性方程式、能量方程式、及状态方程式。

１、连续性方程连续性方程反映了气体流动时质量守恒的规律。

定值=⋅=vf mg ω写成微分形式ggd v dv f df ωω-=7-1它给出了流速、截面面积和比容之间的关系。

连续性方程从质量守恒原理推得，所以普遍适用于稳定流动过程，即不论流体的性质如何（液体和气体），或过程是否可逆。

２、能量方程能量方程反映了气体流动时能量转换的规律。

由式（3-8），对于喷管和扩压管中的稳定绝热流动过程，212122)(21h h g g -=-ωω 写成微分形式dh d g -=221ω7-2３、过程方程过程方程反映了气体流动时的状态变化规律。

对于绝热过程，在每一截面上，气体基本热力学状态参数之间的关系：定值=k pv写成微分式0=+vdv k p dp 7-3二、音速和马赫数音速是决定于介质的性质及介质状态的一个参数，在理想气体中音速可表示为kRT kpv a ==7-4因为音速的大小与气体的状态有关，所以音速是指某一状态的音速，称为当地音速。

流速与声速的比值称为马赫数：M ag=ω 7-5利用马赫数可将气体流动分类为：m 2g v 222图7-1管道稳定流动示意图亚声速流动：1<M a g <ω超声速流动：1>M a g >ω 临界流动： 1=Ma g =ω三、促使气体流速变化的条件 1、力学条件由式（3-5），对于开口系统可逆稳定流动过程，能量方程⎰-∆=21vdp h q 或 vdp dh q -=δ，式中0=q δ所以 vdp dh = 7-6 联合（7-2）和（7-6）vdp d g g -=ωω7-7由式7-7可见，气体在流动中流速变化与压力变化的符号始终相反，表明气流在流动中因膨胀而压力下降时，流速增加；如气流被压缩而压力升高时，则流速必降低。

传热学-第七章换热器

传热学-第七章换热器

1
qmc min qmc max
exp（
NTU）1
qmc min qmc max
第七章 换热器
当冷热流体之一发生相变时，即 qmc max 趋于无穷大
时，于是上面效能公式可简化为
1 exp NTU
当两种流体的热容相等时， 公式可以简化为
顺流：
逆流：
1 exp 2NTU
第七章 换热器
a、增加流速 增加流速可改变流态，提高紊流强度。
b、流道中加插入物增强扰动
在管内或管外加进插入物，如金属丝、 金属螺旋环、盘片、麻花铁、翼形物，以及 将传热面做成波纹状等措施都可增强扰动、 破坏流动边界层，增强传热。
第七章 换热器
c、采用旋转流动装臵 在流道进口装涡流发生器，使流体在一
（3）由冷、热流体的4个进、出口温度确定平均温
差，计算时要注意保持修正系数 具有合适
的数值。
（4）由传热方程求出所需要的换热面积 A，并核算
换热面两侧有流体的流动阻力。 （5）如流动阻力过大，改变方案重新设计。
第七章 换热器
对于校核计算具体计算步骤：
（1）先假设一个流体的出口温度，按热平衡式计 算另一个出口温度
第七章 换热器
7.1 换热器简介 用来使热量从热流体传递到冷流体，
以满足规定的工艺要求的装置统称换热器。
分为间壁式、混合式及蓄热式（或称回热 式）三大类。
第七章 换热器
1、间壁式换热器的主要型式 （1）套管式换热器
图7-1 套管式换热器
适用于传热量不大或流体流量不大的情形。
第七章 换热器
（2）壳管式换热器 这是间壁式换热器的一种主要形式，又
(t1
t2
)

传热学-7热辐射的基本定律

传热学-7热辐射的基本定律
辐射力E： 辐射力E
单位时间内， 单位时间内，物体的单位表面积向半球空间发 射的所有波长的能量总和。 (W/m2)； 射的所有波长的能量总和。 从总体上表征物体发射辐射能本领的大小。 从总体上表征物体发射辐射能本领的大小。
光谱辐射力Eλ： 光谱辐射力E
单位时间内，单位波长范围内( 单位时间内，单位波长范围内(包含某一给定 波长) 波长)，物体的单位表面积向半球空间发射的 能量。 (W/m3)； 能量。
∆Eb =
∫λ
λ2
1
E bλ d λ
黑体辐射函数: 黑体辐射函数:
通常把波段区间的辐射能表示 为同温度下黑体辐射力（ 为同温度下黑体辐射力（λ从0 到∞的整个波谱的辐射能）的百 的整个波谱的辐射能） 的整个波谱的辐射能 分数， 分数，记作 Fb ( λ −λ。 )
Fb ( λ1 −λ2 )
f (λT ) 黑体辐射函数
α + ρ + τ =1
图7.2 物体对热辐射的吸收反射和穿透
对于大多数的固体和液体：τ = 0 , α + ρ = 1 对于大多数的固体和液体： 对于不含颗粒的气体： 对于不含颗粒的气体：
ρ = 0, α + τ = 1
为研究辐射特性可提出以下理想辐射模型： 为研究辐射特性可提出以下理想辐射模型： 黑体： τ=0； 黑体：α=1 ρ=0 τ=0； 白体： τ=0； 白体：α=0 ρ=1 τ=0； 透明体：α=0 ρ=0 τ=1 透明体：
Ebλ =
c1λ−5 ec
2
( λT )
−1
式中， 波长， 式中，λ— 波长，m ；
T — 黑体温度，K ； 黑体温度，
c1 — 第一辐射常数，3.742×10-16 W⋅m2； 第一辐射常数，3.742× c2 — 第二辐射常数，1.4388×10-2 W⋅K； 第二辐射常数，1.4388×

传热学七（ＰＤＦ）

传热学七（ＰＤＦ）
穿透现象。根据能量守恒有
Q = Qα + Qρ + Qτ Qα + Qρ + Qτ = 1 Q QQ
α + ρ + τ = 1
α－吸收率，－ρ 反射率，－τ穿透率（透射率）
在一般情况下，对于固体和液体(强吸收性介质)而言τ很小 可以忽略不计， ρ+α=1
原因：因分子间排列非常紧密，当热辐射能投射到固体表 表面时，马上被相邻的分子所吸收
[例]：教材P244例7-1 解：……由此例可见，黑体或实际物体当T升高时λm减小， 可见光及可见光中短波增加。
3.斯蒂芬-玻尔兹曼(Stefan-Boltzmann)定律
∫ = Eb
∞
= 0 Ebλ d λ
σbT 4
σ b = 5.67 ×10−8 斯蒂芬－波尔兹曼常数，W (m2 ⋅ K4 )
∆Eb
=λ2 λ1
Ebλ
dλ
定义：
F = b(λ1 −λ2 )
∆= Eb Eb
∫ λ2 λ1
Ebλ d λ
=
∞
∫0 Ebλ d λ
∫ 1
σT 4
λ E d λ2
λ1
bλ
(∫ ∫ ) =1 σT 4
λ λ λ2
0
Ebλ d
−
λ1 0
Ebλ
d
= F − F b(0−λ2 )
b(0−λ1 )
Fb(0-λ)为能量份额，意即波长从0至λ的黑体辐射占同温度下黑 体辐射力的百分数。而且：
L(θ ) = dφ (θ ) dA cosθ d Ω
n θ dΩ
dAcosθ dA
3). Lambert定律 表述为：黑体的定向辐射强度与方向无关。 即：

传热学-7 凝结和沸腾传热

传热学-7 凝结和沸腾传热

7-2 沸腾传热
2 汽泡的存在条件
汽泡半径R必须满足下列条件才能存活(克拉贝
龙方程)
R
Rmin
2 Ts rv (tw
ts
)
可见， (tw – ts ) , Rmin 同一加热面上，汽化核 心的凹穴数量增加 汽化核心数增加 换热增强
7-2 沸腾传热
二 大容器沸腾 1 饱和沸腾曲线 大容器沸腾：指加热壁面沉浸在具有自由表面的液 体中所发生的沸腾。 特点：产生的气泡能自由浮升，穿过液体自由面进 入容器空间。 大容器饱和沸腾曲线：表征了大容器饱和沸腾的全 部过程，共包括4个换热规律不同的阶段：自然对 流、核态沸腾、过渡沸腾和稳定膜态沸腾。
7-2 沸腾传热
饱和沸腾：液体主体温度达到饱和温度，壁面温度 高于饱和温度所发生的沸腾。 特点：随着壁面过热度的增高，出现 4 个换热规律 全然不同的区域。
过冷沸腾：液体主体温度低于相应压力下饱和温度， 壁面温度大于该饱和温度所发生的沸腾换热。
7-2 沸腾传热
产生沸腾的条件： 理论分析与实验证明，产生沸腾的条件： 1）液体必须过热； 2）要有汽化核心。 一 汽泡动力学简介 1 汽泡的成长过程 实验表明，通常情况下，沸腾时汽泡只发生在加 热面的某些点，而不是整个加热面上，这些产生气 泡的点被称为汽化核心，较普遍的看法认为，壁面 上的凹穴和裂缝易残留气体，是最好的汽化核心。
7-1 凝结传热
3. 过热蒸气 要考虑过热蒸气与饱和液的焓差。
4. 液膜过冷度及温度分布的非线性 如果考虑过冷度及温度分布的实际情况，要用
下式代替计算公式中的 r，
r r 0.68cp( ts tw )
5. 管子排数 管束的几何布置、流体物性都会影响凝结换热。
6. 凝结表面的几何形状

传热学-第七章

传热学-第七章
(2)蒸汽分压力的下降，使相应的饱和温度下降，则减小了 凝结的驱动力，也使凝结过程削弱。
2. 蒸气流速
流速较高时，蒸气流对液膜表面产生明显的粘滞应力。 如果蒸气流动与液膜向下的流动同向时，使液膜拉薄，h增 大；反之使h减小。
3. 过热蒸气 对于过热蒸汽，应进行修正，只须用过热蒸汽与饱和液
λ = 68.6 ×10−2 w/(mK)
η = 227.6 ×10-6 kg/(ms) ρ = 939 kg/m3
1
δ
=
⎡ 4 × 227 .6 × 10 −6 × 68 .6 × 10 −2 (127 .2
⎢ ⎢⎣
9.81 × 939 2 × 2181 .8 × 10 3
− 123 )x ⎤ 4
n=10 即应安装10个泻液盘
§7-3 膜状凝结的影响因素及其传热强化
工程实际中所发生的膜状凝结过程往往比较复杂，受各 种因素的影响。 1. 不凝结气体
(1)在靠近液膜表面的蒸汽侧，随着蒸汽的凝结，蒸汽分压 下降，不凝结气体的分压上升，液体在抵达液膜表面凝结前， 必须以扩散方式穿过积聚在界面附近的不凝结气体层。因此， 它的存在增加了传递过程(凝结)的阻力。
凝结换热的特点
膜状凝结：沿整个壁面形成一层薄膜，并且 在重力的作用下流动，凝结放出的汽化潜热 g 必须通过液膜，因此，液膜厚度直接影响了 热量传递。
珠状凝结：壁面上是许多小液珠，壁面的部 分表面与蒸汽直接接触，因此，换热速率远 g 大于膜状凝结（可能大几倍，甚至一个数量 级）
tw ts tw< ts 蒸汽空间
−1 2
s
⎜⎜⎝⎛
Pr Pr
w s
⎟⎟⎠⎞ 4 ⎜⎜⎝⎛ Re
3
4 − 253

章熙民传热学第七章

章熙民传热学第七章

第七章7-3 水平冷凝器内，干饱和水蒸断气对压强为 ×105Pa ，管外径16mm ，长为2.5m ，已知第一排每根管的换热量为×104J/s ，试肯定第一排管的凝结表面传热系数及管壁温度。

解：干饱和蒸汽在水平管外凝结。

每根管的凝结热流量 ()w s hA t hA t t Φ∆-== (1)由讲义附录查得，压强Pa ⨯51.9910对应的饱和温度 s t=120℃、潜热r=2202.3kJ /kg 。

计算壁温需要首先计算对流换热系数h 。

而h 又与壁温有关。

先设定壁温为w t =100℃，则凝液的平均温度为s w t t 120100t 1102+==+=℃2 查水的物性参数422.5910/N s m μ-=⨯⋅，3951.0/kg m ρ=，0.685/()W m k λ=⋅管外层流凝结换热的换热系数14[]()s w g r d t t ρλμ-23h=0.725 2331/44951.09.80.6852202.3100.725[]2.59100.016(120100)-⨯⨯⨯⨯⨯⨯⨯⨯-h=212025.67/()W m k ⋅h= 代入式（1）4w s 3.0510t t 120-hA 12025.67 3.140.016 2.5Φ⨯-=⨯⨯⨯= (1)w t 99.8C ︒=与假定的壁温值很接近。

所以壁温约为100C ︒，冷凝换热系数为212025.67/()W m k ⋅。

7-7 垂直列上有20排管的顺排冷凝器，水平放置，求管制的平均表面传热系数与第一排的表面传热系数之比。

解：单排时141[]()s w g r d t t ρλμ-23h =0.725N=20排时()14n []n ()s w g r d t t ρλμ-23h =0.725()231414231140.725[]()1()0.725[]()s w n s w g r nd t t h g r h nd t t ρλμρλμ-==- 1411()0.47220n h h == 可见多排管子冷凝换热比单排的弱。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第七章 凝结与沸腾传热气态工质在饱和温度下，由气态转变为液态的过程称为凝结或冷凝；而液态工质在饱和温度下以产生气泡的形式转变为气态的过程称为沸腾。

第一节 凝结传热二、膜状凝结传热 1.层流膜状凝结理论解图7-1 膜状凝结传热膜内温度及速度场在建立并求解液膜运动微分方程及能量微分方程中，努氏对液膜的速度场和温度场，如图7-1（a ）所示，作了若干合理的设定，把它简化为图7-1（b ）的情况，这些设定是：(1) 纯蒸气在壁上凝结成层流液膜，且物性为常量；(2) 液膜表面温度t δ = t s （饱和温度），即蒸气—液膜交界面无温度梯度，这样，在交界面上仅发生凝结传热而无对流传热与辐射传热； (3) 蒸气是静止的，且认为蒸气对液膜表面无黏滞应力作用，故液膜表面0y u y δ=⎛⎫∂= ⎪∂⎝⎭； (4) 液膜很薄且流动速度缓慢，可忽略液膜的惯性力和对流作用； (5) 凝结热以导热方式通过液膜，因为液膜薄，膜内温度视为线性分布； (6) 忽略液膜的过冷度，即凝结液的焓为饱和液体的焓H'，（实际凝结液的温度将低于饱和温度t s ，故蒸气不但释放出潜热，还有显热，但两者中潜热远大于显热，以致可以忽略显热）。

在建立并求解液膜运动微分方程及能量微分方程中，努氏对液膜的速度场和温度场，如图7-1（a ）所示，作了若干合理的设定，把它简化为图7-1（b ）的情况，这些设定是：（1）纯蒸气在壁上凝结成层流液膜，且物性为常量；（2）液膜表面温度t δ = t s （饱和温度），即蒸气—液膜交界面无温度梯度，这样，在交界面上仅发生凝结传热而无对流传热与辐射传热；（3）蒸气是静止的，且认为蒸气对液膜表面无黏滞应力作用，故液膜表面0y u y δ=⎛⎫∂= ⎪∂⎝⎭； （4）液膜很薄且流动速度缓慢，可忽略液膜的惯性力和对流作用； （5）凝结热以导热方式通过液膜，因为液膜薄，膜内温度视为线性分布； （6）忽略液膜的过冷度，即凝结液的焓为饱和液体的焓H'，（实际凝结液的温度将低于饱和温度t s ，故蒸气不但释放出潜热，还有显热，但两者中潜热远大于显热，以致可以忽略显热）。

22d d u u pu u v g x y x y ρρμ⎛⎫⎛⎫∂∂∂+=-+ ⎪ ⎪∂∂∂⎝⎭⎝⎭（1）d d px= ρv g ()2v 2d 0d ug yμρρ+-= 因为在一般压力条件下，ρ≫ρv ，上式变为22d 0d ug yμρ+= （2）y = 0， u =0 y = δ，d 0d uy= 212g u y y ρδμ⎛⎫=- ⎪⎝⎭（3） y = 0， u =0 y = δ，d 0d uy=212g u y y ρδμ⎛⎫=- ⎪⎝⎭（3） 22d 0d ty = （4） y = 0； t = t w y = δ； t = t s t = t w +（t s - t w ）yδ（5）y = 0， u =0 y = δ，d 0d uy= 212g u y y ρδμ⎛⎫=- ⎪⎝⎭（3） 22d 0d ty = （4） y = 0； t = t w y = δ； t = t s t = t w +（t s - t w ）yδ（5） 23d 3g M u y δρδρμ==⎰（kg/s ） （6）d d d d d d d d d d d M M Mx x x x δδδδ== 将式（6）代入得 22d d g M ρδδμ= （7）wd d d d d d d t M H M MH x H M x y x λ⎛⎫⎛⎫''''+=++ ⎪ ⎪⎝⎭⎝⎭22s w d =()d t t g r x ρδδλμδ-3s w 2()d d t t xgrλμδδρ-=（8）()1/4s w 24x t t gr μλδρ-⎡⎤=⎢⎥⎣⎦ （9）s w x s w ()()d d t t h t t x x λδ--=∴ xh λδ=1/423x s w 4()g r h x t t ρλμ⎡⎤=⎢⎥-⎣⎦ （7-1a ）1/423s w 014d 0.9433()lx x l g r h h x h l l t t ρλμ=⎡⎤===⎢⎥-⎣⎦⎰ [W/(m 2·K)] （7-1b ） 1/423s w 0.725()g r h d t t ρλμ⎡⎤=⎢⎥-⎣⎦[W/(m 2·K)] （7-2a ） 2. 层流膜状凝结传热准则关联式图7-2 液膜的流动图7-3 垂直壁膜状凝结理论解与实验关联式的比较图7－4 层流液膜表面波动凝结液膜雷诺数c ReRe c =e md u ν=e m d u ρμ（10）∴ Re c =m 4u δρμ=4Mμ（7-3）s w ()h t t l rM -= （11）Re c =s w 4()hl t t rμ- （7-4）凝结准则CoCo =1/3322g h λρμ-⎡⎤⎢⎥⎣⎦为无量纲数群Co =1/332hl gl λν-⎡⎤⎢⎥⎣⎦=Nu ·Ga -1/3，Ga 称伽利略（Galileo ）准则垂直壁理论解 Co =1.47 Re c -1/3 （7-1c ） 水平管理论解 Co =1.51 Re c -1/3 （7-2b ）1/423s w 1.13()g r h l t t ρλμ⎡⎤=⎢⎥-⎣⎦ [W/（m 2·K ）] （7-5a ） 或 1/31.76c Co Re -= （7-5b ）c1.22c 1.08 5.2Re Co Re =- （7-6）3. 紊流膜状凝结当c Re >1800时c0.50.75c 875058(253)Re Co Pr Re -=+- （7-7）c c t (1)lx xh h h l l=+- （12） 4.水平管内凝结传热图7－5 水平管内低速蒸气凝结v m,v v v v v=u d G dRe ρμμ=当Re v < 35000时，可采用下式估算平均表面传热系数1/43v s w ()0.555()g r h d t t ρρρλμ⎡⎤'-=⎢⎥-⎣⎦ （7-8）p s w3()8r r c t t '=+- （7-9） 5. 水平管束管外平均表面传热系数图7－6 水平管束凝结液三、影响膜状凝结的因素及增强传热的措施 1. 影响因素 (1)蒸气速度 (2)蒸气含不凝气体 (3)表面粗糙度 (4)蒸气含油 (5)过热蒸气2. 增强凝结传热的措施 (1)改变表面几何特征 (2)有效地排除不凝气体(3)加速凝液的排除 加装中间导流装置、使用离心力、低频振动和静电吸引等方法加速凝液的排泄。

(4)采用能形成珠状凝结的表面第二节 沸 腾 传 热2－1 大空间沸腾传热一、饱和沸腾过程和沸腾曲线图7-7 大空间沸腾曲线（水,1.013Pa 510 ）二、泡态沸腾机理图7-8气泡上的作用力图7-9气泡在核化点上生成图 7-10气泡在壁上的形状c h 及随p 的变化图7-11 大空间沸腾水的c q 、c t ∆、v d ()d d l W p p V A σ=-- v l ()d d p p V A σ-=对于球形 343V R π=，24A R π=，代入上式，微分，得到v l 2()p p Rσ-=（1） v l 2()p p Rσ->（2） 近似表达v s v s d ()()d l pp p t t T-=- （3） v s s v d ()=d ()l l r p T T ρρρρ- （4） 式中，p v 及p l 分别为气泡内蒸气和沸腾液体的密度，kg/m 3。

当沸腾远离临界点时，p v ≪p l ，则式（4）简化为v s sd ()=d r pT T ρ （5）式中，r 为饱和温度下的汽化潜热，J/kg 。

将式（5）代入式（3），再由式（1）可得sv v s2()T R r t t σρ=- （6）sm i n v 2T R r tσρ=∆ （7）三、大空间泡态沸腾表面传热系数的计算()1/41/2c v l v 24q r g πρσρρ=-⎡⎤⎣⎦ （7-10）l v p w ,(),,,,,,h f t g r c C ρρσλμ⎡⎤=∆-⎣⎦（8） 0.70.10.533h q p = [W/（m 2·K ）] （7-11a ） 由q ＝h △t ，上式亦可写为2.3300.122h t p =∆ [W/（m 2·K ）] （7-11b ） 式中 p －沸腾绝对压强，Pa ； q －热流密度，W/m 2； △t －沸腾温差t w －t s ，℃。

2．罗森瑙（Rohsennow ）关联计算式：31/2p ,w s v sw,()()Pr l l l l l c t t g q r C r ρρμσ⎡⎤--⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦（W/m 2） （7-12） 水s ＝1.0；对其他液体s =1.7。

C w,l 值 表7-1图7-12 多孔表面的沸腾2-2 管内沸腾传热简述图7-13 垂直管内沸腾图7-14 水平管内沸腾ht07 .doc 第七章11第三节热管图7-15 热管工作原理1-蒸发段；2-绝热段；3-凝结段；4-管芯；5-液态工质；6-气态工质蒸气1热管的加热区（蒸发段）；2蒸汽输送区（绝热段）；3散热区（凝结段）。