卡尔曼滤波与组合导航-第三讲

卡尔曼滤波算法及其在组合导航中的应用综述摘要:由于描述系统特性的数学模型和噪声的统计模型不准确,不能真实反映物理过程,使模型与获得的观测值不匹配从而会导致滤波器发散。

文章在描述组合导航基本特性和卡尔曼滤波原理的基础上提出了滤波发散的问题并提出了抑制发散的方法,最后介绍了卡尔曼滤波在组合导航中的应用。

关键词:卡尔曼滤波;组合导航;发散随着计算机技术的迅速发展,它有条件提供运算速度高、存贮量大的机载计算机,这为组合导航系统的发展创造了一个很好的技术条件,现代控制理论中最优估计理论的数据处理方法为组合导航系统提供了理论基础。

Kalman滤波是R.E.Kalman于1960年提出的从众多与被提取信号有关的观测量中通过算法估计出所需信号的一种滤波算法。

他把状态空间的概念引入到随机估计理论中,把信号过程视为白噪声作用下的一个线性系统的输出,用状态方程来描述这种输入-输出关系,估计过程中利用系统状态方程、观测方程、系统噪声和观测噪声的统计特性形成滤波算法。

1组合导航系统基本特性描述要描述一个实际系统,首先要对其进行建模,即建立系统的状态方程和测量方程。

对于组合导航系统,要进行滤波计算必须建立数学模型,此模型具有以下特点。

1.1非线性组合导航系统本质上是非线性系统,有时为了减少计算量及提高系统实时性,在某些假设条件下组合导航系统的非线性因素可以忽略,其可以用线性化的数学模型来近似描述。

但当假设条件不满足时,组合导航系统就必须采用能反映自身实际特性的非线性模型来描述。

所以说,非线性是组合导航系统本质的特性。

1.2模型不确定性组合导航系统处于实际运行环境当中时,受系统本身以及外部应用环境不确定性因素的影响,系统实际模型与建立的理论模型不能完全匹配,即组合导航系统具有模型不确定性。

造成系统模型不确定性的主要原因如下:①模型简化。

采用较少的状态变量来描述系统,忽略掉实际系统某些不重要的状态特征。

由此造成模型与实际不匹配。

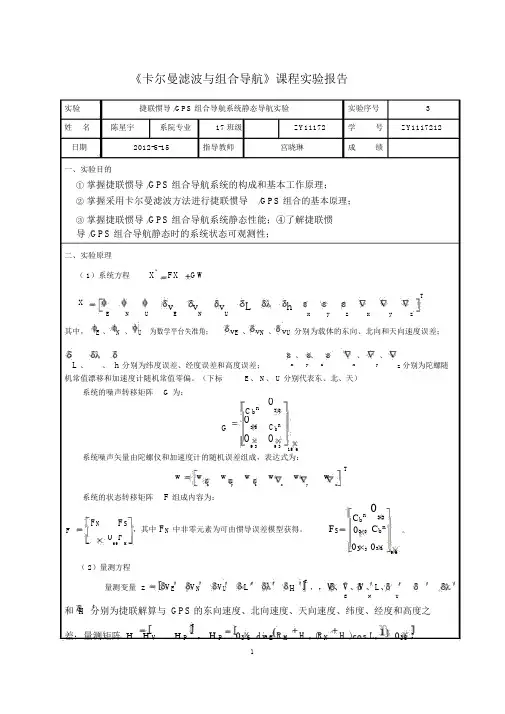
《卡尔曼滤波与组合导航》课程实验报告实验捷联惯导 /GPS 组合导航系统静态导航实验实验序号 3姓名陈星宇系院专业17班级 ZY11172 学 号 ZY1117212日期2012-5-15指导教师宫晓琳成绩一、实验目的① 掌握捷联惯导 /GPS 组合导航系统的构成和基本工作原理； ② 掌握采用卡尔曼滤波方法进行捷联惯导/GPS 组合的基本原理；③ 掌握捷联惯导 /GPS 组合导航系统静态性能；④了解捷联惯导 /GPS 组合导航静态时的系统状态可观测性；二、实验原理（ 1）系统方程 X FX GWXTE NUvEvNvULhx y z x y z其中， E 、 N 、 U 为数学平台失准角；v E 、 v N 、 v U 分别为载体的东向、北向和天向速度误差；L 、 、 h 分别为纬度误差、经度误差和高度误差；x 、 y 、 z、x、y、z 分别为陀螺随机常值漂移和加速度计随机常值零偏。

（下标E 、 N 、 U 分别代表东、北、天）系统的噪声转移矩阵G 为：C b n03 3G03 3C b n9 39 315 6系统噪声矢量由陀螺仪和加速度计的随机误差组成，表达式为：wwwww wTzwxyxyz系统的状态转移矩阵F 组成内容为：F NF SC b n3 3 ，其中 F N 中非零元素为可由惯导误差模型获得。

F S03 3 C b n 。

F069FM03 3 03 39 6（ 2）量测方程量测变量 zV E V NV ULT，，V 、V 、V 、L 、HENU和 H 分别为捷联解算与 GPS 的东向速度、北向速度、天向速度、纬度、经度和高度之差；量测矩阵 H H V H P T03 6 diag R M H , (R N H )cos L,036 ，， H PV 3 3diag 1, 1, 1 0 3 9 ，v v V E v V N v V U v v T H v为量测噪声。

量测噪声方0L H差阵 R 根据GPS的位置、速度噪声水平选取。

基于神经网络和卡尔曼滤波的组合导航技术研究随着位置技术的快速发展和普及，越来越多的人开始关注组合导航技术。

组合导航技术可以通过结合不同的传感器，如惯性测量单位（IMU），GPS，磁场传感器，气压传感器等，准确地估计导航目标的位置、姿态和速度。

其中，神经网络和卡尔曼滤波是组合导航技术中的两种重要方法，它们可以提高导航精度和可靠性。

一、神经网络在组合导航中的应用神经网络是一种模仿人脑的计算模型，它可以通过学习大量的数据，来发现数据之间的联系和规律。

在组合导航中，神经网络可以用来对传感器数据进行处理和融合。

具体来说，可以将来自不同传感器的数据输入给神经网络，让神经网络自己学习数据之间的联系和影响，最终输出更准确和可靠的导航状态信息。

特别地，循环神经网络（RNN）和卷积神经网络（CNN）在组合导航中应用较为广泛。

RNN可以通过记忆之前的状态信息，来更好地处理数据之间的关系，从而适应动态环境下的导航需要；而CNN则可以通过卷积和池化操作，来提取数据中的局部相关性和重要特征，从而减少数据处理的复杂性和耗时。

二、卡尔曼滤波在组合导航中的应用卡尔曼滤波是一种常用的信号处理方法，它可以将传感器数据进行加权平均，从而消除噪声和估计误差。

在组合导航中，卡尔曼滤波可以用来对来自不同传感器的数据进行融合和优化。

具体来说，通过将传感器数据看做随机过程，卡尔曼滤波可以计算出不同传感器数据之间的协方差矩阵和权重系数，然后将这些数据进行融合，得到更加准确和可靠的导航状态信息。

特别地，扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF）在组合导航中应用广泛。

EKF可以通过线性化传感器数据的数学模型，来实现高效的数据融合和优化；而UKF则可以通过样本点来近似系统的状态分布，从而减少对传感器数学模型的依赖和误差。

三、组合导航技术的优化和应用除了神经网络和卡尔曼滤波之外，还有许多其他方法可以用来优化组合导航技术。

例如，可以通过校准传感器数据来降低其误差和漂移，例如使用磁场校正，加速度校正和方向校正等方法；还可以通过优化导航算法的设计和参数，来进一步提高导航精度和可靠性。

目录第1章绪论 (1)1.1课题研究的背景 (1)1.2雷达信号检测与目标跟踪 (2)1.3雷达目标跟踪的基本方法 (3)1.3.1雷达目标跟踪的基本信息 (4)1.3.2目标机动模型 (5)1.3.3雷达目标跟踪的滤波算法 (6)1.3.2.1加权最小二乘滤波 (6)1.3.2.2 滤波 (7)1.4目标跟踪技术有待进一步解决的问题 (8)1.4.1卡尔曼滤波的稳定性和准确性 (8)1.4.2收敛速度的问题 (9)1.4.3滤波过程中的系统偏差的问题 (9)1.5课题来源 (10)1.6本文的主要工作和结构 (11)第2章卡尔曼滤波理论 (12)2.1卡尔曼滤波的基本算法 (12)2.2卡尔曼滤波的性质 (13)2.3 Kalman滤波算法的发展 (14)2.3.1扩展卡尔曼滤波 (16)2.3.2二阶滤波 (17)2.3.3修正增益的扩展卡尔曼滤波 (17)2.3.4自适应扩展卡尔曼滤波 (18)2.3.5基于加权测量噪声协方差矩阵的发散抑制方法 (18)2.4卡尔曼滤波模型 (19)2.5船舶运动目标建模的主要方法 (20)2.6卡尔曼滤波算法中线性化的误差 (21)2.7卡尔曼滤波的应用意义 (22)第3章改进的卡尔曼滤波算法 (24)3.1野值识别与处理 (24)3.1.1野值的识别 (24)3.1.2野值的处理 (25)3.1.3野值处理的仿真分析 (26)3.2目标运动模型的建立 (27)3.2.1Singer模型中的匀速运动目标的运动模型 (27)3.2.2Singer模型中的匀加速运动目标的运动模型 (28)3.3坐标转换 (28)3.4通过自适应选择状态噪声协方差矩阵Q来提高滤波稳定性的方法 (29)3.4.1滤波仿真 (31)3.4.1.1状态协方差矩阵对滤波结果的影响 (31)3.4.1.2对状态噪声协方差矩阵自适应选择以后的滤波结果仿真 (33)3.5双模型并行滤波构造 (34)3.5.1滤波构造的设计 (35)3.5.2模拟仿真 (36)3.5.2.1基础卡尔曼滤波的仿真结果 (36)3.5.2.2并行滤波仿真结果 (38)4.1简化卡尔曼滤波算法发展现状 (40)4.1.1常增益滤波 (40)4.1.2状态约减 (40)4.1.3分段卡尔曼滤波 (40)4.1.4解藕卡尔曼滤波 (41)4.2本文简化算法设计方法 (41)4.3模拟仿真 (44)4.3.1简化算法与未简化算法的精度比较 (44)4.3.2 K值组的数量对滤波结果的影响 (45)第五章对卡尔曼滤波的展望 (48)结论 (49)参考文献 (50)第1章绪论1.1课题研究的背景雷达目标跟踪是整个雷达系统中一个非常关键的环节。