椭圆 椭圆的几何性质

e越接近1，椭圆越扁；e越接近 于0，椭圆越接近于圆。
2 2 例1：椭圆25x +16y =400
的长轴长为____，短轴长 为____，焦点坐标为___， 顶点坐标为____，离心率 为 ______。
x y 练习：若椭圆 1的离心率 a8 9 1 为 ，求a的值。 2
2
2
x y (2)若 2 2 1( a b 0 ) 的左焦 a b
x y 2 1 2 a b ( a b 0)
y B2(0,b) o x A2(a,0) B1(0,-b)
2
2
A1(-a,0)
a、b分别叫做椭圆的 长半轴长和短半轴长。
四、椭圆的离心率
离心率：椭圆的焦距与长轴长的比, 2c c 叫做椭圆的离心率。 e y 2a a
0<e<1
o x
变式： (08江西)已知F1，F2椭圆的两 个焦点，满足 MF1 MF2 0 ，点 M总在椭圆的内部，则椭圆的离心率 的取值范围是___________。
2
2
练习：
2 2
x y 1 ( a b 0 ) 已知 2 2 a b 的长轴两端点为A，B，如果椭圆 上存在一点Q，使∠F1QF2=120°， 求离心率e的取值范围。
一、椭圆的范围 二、椭圆的对称性 三、椭圆的顶点
变量x，y的取 值范围 方程的对称性 x=0或y=0时 方程的解
四、椭圆2 2 2 2 x y x y 由 2 1 2 1和 2 1 2 a b a b
即
x a和 y b
o
y
说明：椭圆位于矩 形之中。
x
二、椭圆的对称性 2 2
椭圆关于x轴对称； 椭圆关于y轴对称； 椭圆关于原点对称；

Evaluation Warning: The document was created with Spire.Doc for JA V A.（一）椭圆的定义：1、椭圆的定义：平面内与两个定点1F 、2F 的距离之和等于定长（大于12||F F ）的点的轨迹叫做椭圆。

这两个定点 1F 、2F 叫做椭圆的焦点，两焦点的距离12||F F 叫做椭圆的焦距。

对椭圆定义的几点说明： （1）“在平面内”是前提，否则得不到平面图形（去掉这个条件，我们将得到一个椭球面）；（2）“两个定点”的设定不同于圆的定义中的“一个定点”，学习时注意区分； （3）作为到这两个定点的距离的和的“常数”，必须满足大于| F 1F 2|这个条件。

若不然，当这个“常数”等于| F 1F 2|时，我们得到的是线段F 1F 2；当这个“常数”小于| F 1F 2|时，无轨迹。

这两种特殊情况，同学们必须注意。

（4）下面我们对椭圆进行进一步观察，发现它本身具备对称性，有两条对称轴和一个对称中心，我们把它的两条对称轴与椭圆的交点记为A 1， A 2， B 1， B 2，于是我们易得| A 1A 2|的值就是那个“常数”，且|B 2F 2|+|B 2F 1|、|B 1F 2|+|B 1F 1|也等于那个“常数”。

同学们想一想其中的道理。

（5）中心在原点、焦点分别在x 轴上，y 轴上的椭圆标准方程分别为：22222222x y y x 1(a b 0),1(a b 0),a b a b +=>>+=>> 相同点是：形状相同、大小相同；都有 a > b > 0 ，222a cb =+。

不同点是：两种椭圆相对于坐标系的位置不同，它们的焦点坐标也不同（第一个椭圆的焦点坐标为（－c ，0）和（c ，0），第二个椭圆的焦点坐标为（0，－c ）和（0，c ）。

椭圆的焦点在 x 轴上⇔标准方程中x 2项的分母较大；椭圆的焦点在 y 轴上⇔标准方程中y 2项的分母较大。

椭圆的定义及几何性质椭圆【教学目标】（1）掌握椭圆的定义（2）掌握椭圆的几何性质（3）掌握求椭圆的标准方程【教学重难点】（1）椭圆的离心率有关的问题（2）椭圆焦点三角形面积的求法【教学过程】一、知识点梳理知识点一：椭圆的定义平面内一个动点到两个定点、的距离之和等于常数()，这个动点的轨迹叫椭圆。

这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距。

注意：若，则动点的轨迹为线段；若，则动点的轨迹无图形。

知识点二：椭圆的标准方程1．当焦点在轴上时，椭圆的标准方程：，其中；2．当焦点在轴上时，椭圆的标准方程：，其中；注意：．只有当椭圆的中心为坐标原点，对称轴为坐标轴建立直角坐1椭圆的定义及几何性质标系时，才能得到椭圆的标准方程；2．在椭圆的两种标准方程中，都有和；3．椭圆的焦点总在长轴xx.当焦点在轴xx时，椭圆的焦点坐标为，；当焦点在轴xx时，椭圆的焦点坐标为，。

知识点三：椭圆的简单几何性质椭圆的的简单几何性质（1）对称性对于椭圆标准方程，把x换成―x，或把y换成―y，或把x、y同时换成―x、―y，方程都不变，所以椭圆是以x轴、y轴为对称轴的轴对称图形，且是以原点为对称中心的中心对称图形，这个对称中心称为椭圆的中心。

讲练结合：（2）范围椭圆上所有的点都位于直线x=±a和y=±b所围成的矩形内，所以椭圆上点的坐标满足|x|≤a，|y|≤b。

（3）顶点①椭圆的对称轴与椭圆的交点称为椭圆的顶点。

②椭圆（a＞b＞0）与坐标轴的四个交点即为椭圆的四个顶点，坐标分别为A1（―a，0），A2（a，0），B1（0，―b），B2（0，b）。

③线段A1A2，B1B2分别叫做椭圆的长轴和短轴，|A1A2|=2a，分别叫做椭圆的长半轴长和短半轴长。

b和a。

|B1B2|=2b椭圆的定义及几何性质（4）离心率表示，记exx的比叫做椭圆的离心率，用①椭圆的焦距与长轴作。

，则1。

e越接近10 ②因为a＞c＞，所以e的取值范围是0＜e＜就0，cac就越接近，从而越小，因此椭圆越扁；反之，e越接近于a=b当且仅当这时椭圆就越接近于圆。

e =
c a
a2=b2+c2
已知椭圆方程为16x =400， 例1、已知椭圆方程为16x2+25y2=400，则 它的长轴长是： 10 ；短轴长是 短轴长是： 8 ； 它的长轴长是 短轴长是
焦距是： 焦距是
6
；离心率等于 离心率等于： 离心率等于
焦点坐标是： 焦点坐标是
(±3, 0) ；顶点坐标是 (±5, 0) (0, ±4) ； 顶点坐标是： 顶点坐标是
x2 y2 + = 1 的两个焦点为 1 、F2 ，过左焦点作 的两个焦点为F 椭圆 45 20
直线与椭圆交于A， 两点， 的面积为20， 直线与椭圆交于 ，B 两点，若△ AB F2 的面积为 ， 求直线的方程。 求直线的方程。
y
（x1 , y1） A
o
（x2 , y2） B F1 F2
x
作业
1.已知椭圆的中心在原点，焦点在坐标轴上，长 已知椭圆的中心在原点，焦点在坐标轴上， 已知椭圆的中心在原点 轴是短轴的三倍，且椭圆经过点P（ ， ）， ），求 轴是短轴的三倍，且椭圆经过点 （3，0），求 椭圆的方程. 椭圆的方程 2 2 x + 2 y = 4 的左焦点作倾斜角为 30 0 2.过椭圆 过椭圆 的直线AB， 求线段AB的长度 的长度. 的直线 ， 求线段 的长度
B2
A1
b F1
a F2
A2
o c
B1
3、椭圆的顶点 、
x a
2 2
y2 + = 1( a > b > 0 ) 2 b
顶点：椭圆与它的对称轴的四个交点，叫做椭圆的顶点。 顶点：椭圆与它的对称轴的四个交点，叫做椭圆的顶点。 长轴、短轴：线段 长轴、短轴：线段A1A2、B1B2分别叫做椭圆的长轴和短 轴。 a、b分别叫做椭圆的长半轴长和短半轴长。 a、b分别叫做椭圆的长半轴长和短半轴长。 分别叫做椭圆的长半轴长和短半轴长 y

a2=b2+c2
标准方程 范围 对称性 顶点坐标 焦点坐标 半轴长
离心率
x2 y2 a2 b2 1(a b 0)
|x|≤ a,|y|≤ b
x2 b2

y2 a2
1(a
b

0)
|x|≤ b,|y|≤ a
关于x 轴、y 轴成轴对称；
关于原点成中心对称
(a,0)、(-a,0)、 (0,b)、(0,-b)

(m

n)2
(m2 2

n2 )

2(a 2

c2 ).
m, n 是方程 x2 2ax 2(a2 c2 ) 0 的两个根，
y
P
所以 (2a)2 8(a2 c2 ) ≥ 0 .
2c2 ≥ a2

c2 ≥ 1 a2 2
F1 o
F2
x
主页
例 3.已知 P 是椭圆上一点, F1, F2 分别是椭圆的左右焦点，且 PF1 PF2 ，求离心率的取值范围．

c2 (a c)2

(a c)2 4(a c)2
1
x2 a2

y2 b2
1
所以c2+10ac-3a2=0, 则e2+10e-3=0，
e 2 7 5.
主页
【例
4】设
F1，F2
分别是椭圆
x2 4

y2

1的左右焦点，若
P
是该椭
圆上的一个动点，求 PF1 PF 2 的最大值和最小值．
F1 o
F2
x
2a2 2e2 x02 4c2 ,

x02

椭圆的简单几何性质教学教案一、教学目标1. 知识与技能：使学生掌握椭圆的定义，理解椭圆的基本几何性质，如焦点、半长轴、半短轴等概念；2. 过程与方法：通过观察、分析、归纳等方法，让学生发现并证明椭圆的几何性质；3. 情感态度与价值观：培养学生对数学的兴趣，提高学生分析问题、解决问题的能力。

二、教学内容1. 椭圆的定义：椭圆是平面上到两个定点（焦点）距离之和为定值的点的轨迹。

2. 椭圆的基本几何性质：a. 焦点：椭圆的焦点距离为2c，其中c为半焦距，c^2=a^2-b^2；b. 半长轴：椭圆的半长轴为a，表示椭圆的长轴的一半；c. 半短轴：椭圆的半短轴为b，表示椭圆的短轴的一半；d. 椭圆的面积：S=πab。

三、教学重点与难点1. 教学重点：椭圆的定义及其基本几何性质；2. 教学难点：椭圆的焦点、半长轴、半短轴等概念的理解与应用。

四、教学方法1. 采用问题驱动法，引导学生通过观察、分析、归纳等方法发现椭圆的几何性质；2. 利用数形结合法，让学生直观地理解椭圆的定义及其几何性质；3. 运用实例讲解法，让学生掌握椭圆在实际问题中的应用。

五、教学过程1. 导入新课：通过介绍椭圆的起源和发展，激发学生的学习兴趣；2. 讲解椭圆的定义：结合图形，解释椭圆的定义，让学生理解椭圆的概念；3. 探索椭圆的基本几何性质：引导学生观察椭圆的图形，发现焦点、半长轴、半短轴等性质；4. 证明椭圆的几何性质：引导学生运用数学方法证明椭圆的基本几何性质；5. 应用实例：让学生运用椭圆的性质解决实际问题，巩固所学知识。

本教案为椭圆的简单几何性质教学教案的第一部分，后续章节将陆续呈现。

希望能对您的教学有所帮助！六、教学练习1. 基本概念练习：a. 定义椭圆的焦点；b. 解释椭圆的半长轴和半短轴；c. 计算椭圆的面积。

2. 应用题练习：a. 已知椭圆的半长轴为5cm，半短轴为3cm，求椭圆的焦点距离；b. 已知椭圆的面积为36πcm²，半长轴为6cm，求椭圆的半短轴；c. 一个椭圆的焦点在x轴上，半长轴为4cm，半短轴为3cm，求椭圆的标准方程。

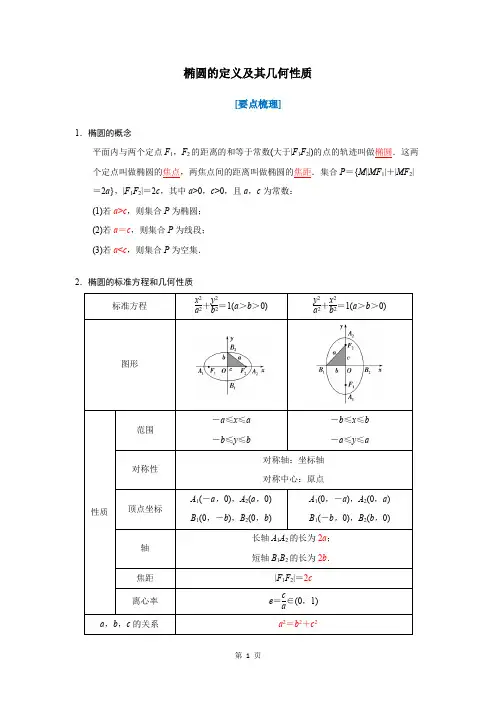
椭圆的定义及其几何性质[要点梳理]1．椭圆的概念平面内与两个定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a>0，c>0，且a，c为常数：(1)若a>c，则集合P为椭圆；(2)若a＝c，则集合P为线段；(3)若a<c，则集合P为空集．2．椭圆的标准方程和几何性质椭圆的常用性质(1)设椭圆x2a2＋y2b2＝1(a>b>0)上任意一点P(x，y)，则当x＝0时，|OP|有最小值b，P点在短轴端点处；当x＝±a时，|OP|有最大值a，P点在长轴端点处．(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形，其中a为斜边，a2＝b2＋c2．(3)已知过焦点F1的弦AB，则△ABF2的周长为4a．[基础自测]一、思考辨析判断下列说法是否正确，正确的在它后面的括号里打“√”，错误的打“×”．(1)平面内与两个定点F1，F2的距离之和等于常数的点的轨迹是椭圆．()(2)椭圆上一点P与两焦点F1，F2构成△PF1F2的周长为2a＋2c(其中a为椭圆的长半轴长，c为椭圆的半焦距)．()(3)椭圆的离心率e越大，椭圆就越圆．()(4)椭圆既是轴对称图形，又是中心对称图形．()(5)方程mx2＋ny2＝1(m＞0，n＞0，m≠n)表示的曲线是椭圆．()(6)x2a2＋y2b2＝1(a＞b＞0)与y2a2＋x2b2＝1(a＞b＞0)的焦距相同．()答案：(1)×(2)√(3)×(4)√(5)√(6)√二、小题查验1．设P是椭圆x225＋y216＝1上的点，若F1，F2是椭圆的两个焦点，则|PF1|＋|PF2|等于()A．4B．5 C．8 D．10解析：D[由椭圆的定义知：|PF1|＋|PF2|＝2×5＝10．]2．已知椭圆x225＋y2m2＝1(m>0)的左焦点为F1(－4，0)，则m＝()A．2 B．3 C．4 D．9解析：B[由题意知25－m2＝16，解得m2＝9，又m>0，所以m＝3．]3．已知椭圆C：x2a2＋y24＝1的一个焦点为(2，0)，则C的离心率为()A ．13B ．12C ．22D ．223解析：C [由椭圆x 2a 2＋y 24＝1知b 2＝4，∴b ＝2，c ＝2，∴a ＝b 2＋c 2＝22．∴椭圆的离心率e ＝c a ＝222＝22．]4．过点A (3，－2)且与椭圆x 29＋y 24＝1有相同焦点的椭圆的方程为( )A ．x 215＋y 210＝1B ．x 225＋y 220＝1C ．x 210＋y 215＝1D ．x 220＋y 215＝1解析：A [由题意知c 2＝5，可设椭圆方程为x 2λ＋5＋y 2λ＝1(λ>0)，则9λ＋5＋4λ＝1，解得λ＝10或λ＝－2(舍去)，∴所求椭圆的方程为x 215＋y 210＝1．]5．若方程x 25－k ＋y 2k －3＝1表示椭圆，则k 的取值范围是__________．解析：由已知得⎩⎪⎨⎪⎧5－k >0，k －3>0，5－k ≠k －3，解得3<k <5且k ≠4． 答案：(3，4)∪(4，5) 三、大题突破1．分别求出满足下列条件的椭圆的标准方程．(1)与椭圆x 24＋y 23＝1有相同的离心率且经过点(2，－3)；(2)已知点P 在以坐标轴为对称轴的椭圆上，且P 到两焦点的距离分别为5，3，过P 且 与长轴垂直的直线恰过椭圆的一个焦点．解：(1)由题意，设所求椭圆的方程为x 24＋y 23＝t 1或y 24＋x 23＝t 2(t 1，t 2＞0)，因为椭圆过点(2，－3)，所以t 1＝224＋（－3）23＝2，或t 2＝（－3）24＋223＝2512.故所求椭圆的标准方程为x 28＋y 26＝1或y 2253＋x 2254＝1.(2)由于焦点的位置不确定，所以设所求的椭圆方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)或y 2a 2＋x 2b 2＝1(a ＞b＞0)，由已知条件得⎩⎪⎨⎪⎧2a ＝5＋3，（2c ）2＝52－32，解得a ＝4，c ＝2，所以b 2＝12. 故椭圆方程为x 216＋y 212＝1或y 216＋x 212＝1.2．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)经过点(2，1)，且离心率为22.(1)求椭圆C 的方程；(2)设M ，N 是椭圆上的点，直线OM 与ON (O 为坐标原点)的斜率之积为－12.若动点P满足OP →＝OM →＋2ON →，求点P 的轨迹方程．解：(1)因为e ＝22，所以b 2a 2＝12，又椭圆C 经过点(2，1)，所以2a 2＋1b 2＝1，解得a 2＝4，b 2＝2，所以椭圆C 的方程为x 24＋y 22＝1.(2)设P (x ，y )，M (x 1，y 1)，N (x 2，y 2)，则由OP →＝OM →＋2ON →得x ＝x 1＋2x 2，y ＝y 1＋2y 2， 因为点M ，N 在椭圆x 24＋y 22＝1上，所以x 21＋2y 21＝4，x 22＋2y 22＝4，故x 2＋2y 2＝(x 21＋4x 1x 2＋4x 22)＋2(y 21＋4y 1y 2＋4y 22)＝(x 21＋2y 21)＋4(x 22＋2y 22)＋4(x 1x 2＋2y 1y 2)＝20＋4(x 1x 2＋2y 1y 2)．设k OM ，k ON 分别为直线OM 与ON 的斜率，由题意知， k OM ·k ON ＝y 1y 2x 1x 2＝－12，因此x 1x 2＋2y 1y 2＝0，所以x 2＋2y 2＝20，故点P 的轨迹方程为x 220＋y 210＝1.第1课时 椭圆的定义及简单几何性质[考点梳理]1．已知两圆C 1：(x －4)2＋y 2＝169，C 2：(x ＋4)2＋y 2＝9，动圆在圆C 1内部且和圆C 1相内切，和圆C 2相外切，则动圆圆心M 的轨迹方程为( )A ．x 264－y 248＝1B ．x 248＋y 264＝1C ．x 248－y 264＝1D ．x 264＋y 248＝1[解析] 设圆M 的半径为r ，则|MC 1|＋|MC 2|＝(13－r )＋(3＋r )＝16，又|C 1C 2|＝8＜16，∴动圆圆心M 的轨迹是以C 1、C 2为焦点的椭圆，且2a ＝16,2c ＝8，则a ＝8，c ＝4，∴b 2＝48，故所求的轨迹方程为x 264＋y 248＝1．2．F 1，F 2是椭圆x 29＋y 27＝1的两个焦点，A 为椭圆上一点，且∠AF 1F 2＝45°，则△AF 1F 2的面积为( )A ．7B ．74C ．72D ．752[解析] 由题意得a ＝3，b ＝7，c ＝2， ∴|F 1F 2|＝22，|AF 1|＋|AF 2|＝6．∵|AF 2|2＝|AF 1|2＋|F 1F 2|2－2|AF 1|·|F 1F 2|cos 45°＝|AF 1|2－4|AF 1|＋8， ∴(6－|AF 1|)2＝|AF 1|2－4|AF 1|＋8．∴|AF 1|＝72，∴S △AF 1F 2＝12×72×22×22＝72．[答案] (1)D (2)C3．设F 1，F 2分别是椭圆E ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的左，右焦点，过点F 1的直线交椭圆E 于A ，B 两点，|AF 1|＝3|F 1B |，且|AB |＝4，△ABF 2的周长为16，则|AF 2|＝________． 解析：由|AF 1|＝3|F 1B |，|AB |＝4，得|AF 1|＝3， ∵△ABF 2的周长为16，∴4a ＝16，∴a ＝4． 则|AF 1|＋|AF 2|＝2a ＝8， ∴|AF 2|＝8－|AF 1|＝8－3＝5．4．已知F 1、F 2是椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的两个焦点，P 为椭圆C 上的一点，且PF 1⊥PF 2，若△PF 1F 2的面积为9，则b ＝________．解析：设|PF 1|＝r 1，|PF 2|＝r 2，则⎩⎪⎨⎪⎧r 1＋r 2＝2a ，r 21＋r 22＝4c 2， 所以2r 1r 2＝(r 1＋r 2)2－(r 21＋r 22)＝4a 2－4c 2＝4b 2，所以S △PF 1F 2＝12r 1r 2＝b 2＝9，所以b ＝3． 答案：(1)5 (2)31．若直线x －2y ＋2＝0经过椭圆的一个焦点和一个顶点，则该椭圆的标准方程为( )A ．x 25＋y 2＝1B ．x 24＋y 25＝1C ．x 25＋y 2＝1或x 24＋y 25＝1D ．x 24＋y 2＝1[解析] C [直线与坐标轴的交点为(0,1)，(－2,0)， 由题意知当焦点在x 轴上时，c ＝2，b ＝1， ∴a 2＝5，所求椭圆的标准方程为x 25＋y 2＝1．当焦点在y 轴上时，b ＝2，c ＝1，∴a 2＝5，所求椭圆的标准方程为y 25＋x 24＝1．] 2．一个椭圆的中心在原点，焦点F 1，F 2在x 轴上，P (2，3)是椭圆上一点，且|PF 1|，|F 1F 2|，|PF 2|成等差数列，则椭圆的标准方程为( )A ．x 28＋y 26＝1B ．x 216＋y 26＝1C ．x 24＋y 22＝1D ．x 28＋y 24＝1[解析] A [设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)．由点P (2，3)在椭圆上知4a 2＋3b 2＝1．又|PF 1|，|F 1F 2|，|PF 2|成等差数列， 则|PF 1|＋|PF 2|＝2|F 1F 2|，即2a ＝2×2c ，c a ＝12，又c 2＝a 2－b 2，联立⎩⎪⎨⎪⎧4a 2＋3b 2＝1，c 2＝a 2－b 2，c a ＝12即a 2＝8，b 2＝6，故椭圆方程为x 28＋y 26＝1．] 3．已知F 1(－1，0)，F 2(1，0)是椭圆的两个焦点，过F 1的直线l 交椭圆于M ，N 两点，若△MF 2N 的周长为8，则椭圆方程为( )A ．x 24＋y 23＝1B ．y 24＋x 23＝1C ．x 216＋y 215＝1D ．y 216＋x 215＝1解析：∵F 1(－1,0)，F 2(1,0)是椭圆的两个焦点，∴c ＝1．根据椭圆的定义，得△MF 2N 的周长为4a ＝8，得a ＝2，∴b ＝3，∴椭圆方程为x 24＋y 23＝1，故选A ．4．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，且与抛物线y 2＝x 交于A ，B 两点，若△OAB (O 为坐标原点)的面积为22，则椭圆C 的方程为( )A ．x 28＋y 24＝1B ．x 22＋y 2＝1C ．x 212＋y 26＝1D ．x 212＋y 28＝1解析：∵椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)与抛物线y 2＝x 交于A ，B 两点∴设A (x ，x )，B (x ，－x )，则x x ＝22，解得x ＝2，∴A (2，2)．由已知得⎩⎨⎧c a ＝22，4a 2＋2b2＝1，a 2＝b 2＋c 2，解得a ＝22，b ＝2．∴椭圆C 的方程为x 28＋y 24＝1，故选A ．答案：(1)A (2)A[命题角度1] 椭圆的长轴、短轴、焦距1．已知椭圆x 2m －2＋y 210－m＝1的长轴在x 轴上，焦距为4，则m 等于( )A ．8B ．7C ．6D ．5 解析：A [∵椭圆x 2m －2＋y 210－m ＝1的长轴在x 轴上，∴⎩⎪⎨⎪⎧m －2>0，10－m >0，m －2>10－m ，解得6<m <10．∵焦距为4，∴c 2＝m －2－10＋m ＝4，解得m ＝8．] [命题角度2] 椭圆的离心率2．已知F 1，F 2是椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点，A 是C 的左顶点，点P 在过A且斜率为36的直线上，△PF 1F 2为等腰三角形，∠F 1F 2P ＝120°，则C 的离心率为( )A ．23B ．12C ．13D ．14解析：D [如图，作PB ⊥x 轴于点B ．由题意可设|F 1F 2|＝|PF 2|＝2，则c ＝1，由∠F 1F 2P ＝120°，可得|PB |＝3，|BF 2|＝1，故|AB |＝a ＋1＋1＝a ＋2， tan ∠P AB ＝|PB ||AB |＝3a ＋2＝36，解得a ＝4．所以e ＝c a ＝14．故选D ．]2．已知F 1，F 2是椭圆C 的两个焦点，P 是C 上的一点，若PF 1⊥PF 2，且∠PF 2F 1＝60°，则C 的离心率为( ) A ．1－32 B ．2－3 C ．3－12D ．3－1 解析：D [在Rt △PF 1F 2中，∠PF 2F 1＝60°，不妨设椭圆焦点在x 轴上，且焦距|F 1F 2|＝2，则|PF 2|＝1，|FP 1|＝3，由椭圆的定义可知，方程x 2a 2＋y 2b 2＝1(a >b >0)中，2a ＝1＋3，2c ＝2，得a ＝1＋32，c ＝1，所以离心率e ＝c a ＝21＋3＝3－1．故选D ．]3．已知F 1，F 2分别是椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点，若椭圆C 上存在点P ，使得线段PF 1的中垂线恰好经过焦点F 2，则椭圆C 离心率的取值范围是( ) A ．[32，1) B ．[31，22] C ．[31，1) D ．(0，31]解析：C [如图所示，∵线段PF 1的中垂线经过F 2， ∴|PF 2|＝|F 1F 2|＝2c ， 即椭圆上存在一点P ， 使得|PF 2|＝2c ．∴a －c ≤2c <a ＋c ．∴e ＝c a ∈⎣⎡⎭⎫13，1．] [命题角度3] 与椭圆有关的最值或范围问题4．已知F 是椭圆C ：x 29＋y 25＝1的左焦点，P 为C 上一点，A (1，34)，则|P A |＋|PF |的最小值为( )A ．103B ．113C ．4D ．133解析：D [设椭圆C ：x 29＋y 25＝1的右焦点为F ′(2,0)，F (－2,0)，由A ⎝⎛⎭⎫1，43，则|AF ′|＝53， 根据椭圆的定义可得|PF |＋|PF ′|＝2a ＝6，所以|P A |＋|PF |＝|P A |＋6－|PF ′|≥6－|AF ′|＝6－53＝133．]5．如图，焦点在x 轴上的椭圆x 24＋y 2b 2＝1的离心率e ＝12，F ，A 分别是椭圆的一个焦点和顶点，P 是椭圆上任意一点，则PF →·P A →的最大值为( )A ．1B ．23C ．4D ．43解析：C [设P 点坐标为(x 0，y 0)． 由题意知a ＝2，∵e ＝c a ＝12，∴c ＝1，∴b 2＝a 2－c 2＝3．所求椭圆方程为x 24＋y 23＝1．∴－2≤x 0≤2，－3≤y 0≤3． 又F (－1,0)，A (2,0)，PF →＝(－1－x 0，－y 0)，P A →＝(2－x 0，－y 0)， ∴PF →·P A →＝x 20－x 0－2＋y 20＝14x 20－x 0＋1＝14(x 0－2)2． 当x 0＝－2时，PF →·P A →取得最大值4．][课时训练]一、选择题1．椭圆x 216＋y 225＝1的焦点坐标为( )A ．(±3，0)B ．(0，±3)C ．(±9，0)D ．(0，±9) 解析：B [根据椭圆方程可得焦点在y 轴上，且c 2＝a 2－b 2＝25－16＝9，∴c ＝3，故焦点坐标为(0，±3)．故选B.]2．已知椭圆的中心在原点，离心率e ＝12，且它的一个焦点与抛物线y 2＝－4x 的焦点重合，则此椭圆方程为( )A ．x 24＋y 23＝1B ．x 28＋y 26＝1C ．x 22＋y 2＝1D ．x 24＋y 2＝1解析：A [依题意，可设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)，由已知可得抛物线的焦点为(－1，0)，所以c ＝1，又离心率e ＝c a ＝12，解得a ＝2，b 2＝a 2－c 2＝3，所以椭圆方程为x 24＋y 23＝1，故选A.] 3．方程kx 2＋4y 2＝4k 表示焦点在x 轴上的椭圆，则实数k 的取值范围是( )A ．k ＞4B ．k ＝4C ．k ＜4D ．0＜k ＜4 解析：D [方程kx 2＋4y 2＝4k表示焦点在x 轴上的椭圆，即方程x 24＋y 2k＝1表示焦点在x轴上的椭圆，可得0＜k ＜4，故选D.]4．若椭圆x 24＋y 2m ＝1上一点到两焦点的距离之和为m －3，则此椭圆的离心率为( )A ．53B ．53或217C ．217D ．37或59解析：A [由题意得，2a ＝m －3>0，即m >3，若a 2＝4，即a ＝2，则m －3＝4，m ＝7>4，不合题意，因此a 2＝m ，即a ＝m ，则2m ＝m －3，解得m ＝9，即a ＝3，c ＝m －4＝5，所以椭圆离心率为e ＝53.故选A.] 5．设椭圆C ：x 2a 2＋y 2b2＝1(a >0，b >0)的左、右焦点分别为F 1，F 2，点E (0，t )(0<t <b )．已知动点P 在椭圆上，且点P ，E ，F 2不共线，若△PEF 2的周长的最小值为4b ，则椭圆C 的离心率为( ) A ．32 B ．22 C ．12 D ．33解析：A [△PEF 2的周长为|PE |＋|PF 2|＋|EF 2|＝|PE |＋2a －|PF 1|＋|EF 2| ＝2a ＋|EF 2|＋|PE |－|PF 1|≥2a ＋|EF 2|－|EF 1|＝2a ＝4b ，∴e ＝c a ＝1－⎝⎛⎭⎫b a 2＝1－14＝32，故选A.] 6．在椭圆x 2a 2＋y 2b2＝1(a >b >0)中，F 1，F 2分别是其左、右焦点，若|PF 1|＝2|PF 2|，则该椭圆离 心率的取值范围是( )A ．(31，1)B ．[31，1)C ．(0，31)D ．(0，31] 解析：B [根据椭圆定义得|PF 1|＋|PF 2|＝2a ，将|PF 1|＝2|PF 2|代入，得|PF 2|＝2a 3，根据椭圆的几何性质，知|PF 2|≥a －c ，故2a 3≥a －c ，即a ≤3c ，故c a ≥13，即e ≥13，又e <1，故该椭圆离心率的取值范围是⎣⎡⎭⎫13，1，故选B.]7．过椭圆x 225＋y 216＝1的中心任意作一条直线交椭圆于P ，Q 两点，F 是椭圆的一个焦点，则 △PQF 周长的最小值是( )A ．14B ．16C ．18D ．20 解析：C [如图，设F 1为椭圆的左焦点，右焦点为F 2，根据椭圆的对称性可知|F 1Q |＝|PF 2|，|OP |＝|OQ |，所以△PQF 1的周长为|PF 1|＋|F 1Q |＋|PQ |＝|PF 1|＋|PF 2|＋2|PO |＝2a ＋2|PO |＝10＋2|PO |，易知2|OP |的最小值为椭圆的短轴长，即点P ，Q 为椭圆的上下顶点时，△PQF 1即△PQF 的周长取得最小值为10＋2×4＝18.]二、填空题8．设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的右焦点与抛物线y 2＝16x 的焦点相同，离心率为63，则此椭圆 的方程为______________.解析：由题意知抛物线y 2＝16x 的焦点为(4，0)，∴c ＝4， ∵e ＝c a ＝4a ＝63，∴a ＝26，∴b 2＝a 2－c 2＝8，∴椭圆的方程为x 224＋y 28＝1. 答案：x 224＋y 28＝1 9．若x 2＋ky 2＝2表示焦点在y 轴上的椭圆，则实数k 的取值范围是____________.解析：将椭圆的方程化为标准形式得y 22k＋x 22＝1，因为x 2＋ky 2＝2表示焦点在y 轴上的椭圆，所以2k>2， 解得0<k <1.答案：(0，1)10．若椭圆的方程为x 210－a ＋y 2a －2＝1，且此椭圆的焦距为4，则实数a ＝________. 解析：由题可知c ＝2.①当焦点在x 轴上时，10－a －(a －2)＝22，解得a ＝4.②当焦点在y 轴上时，a －2－(10－a )＝22，解得a ＝8.故实数a ＝4或8.答案：4或811．若椭圆x 2a 2＋y 2b 2＝1(a >b >0)上存在点P ，使得PF 1→·PF 2→＝0，则椭圆离心率的取值范围是 ______________.解析：因为PF 1→·PF 2→＝0，所以∠F 1PF 2＝90°.设P (x 0，y 0)S △PF 1F 2＝b 2＝c |y 0|≤cb ，即b ≤c ，则a 2－c 2≤c 2，解得e 2≥12，即e ≥22，又在椭圆中0<e <1，故椭圆离心率的取值范围是⎣⎡⎭⎫22，1. 答案：⎣⎡⎭⎫22，1三、解答题12．已知动圆M 过定点A (－3，0)，并且内切于定圆B ：(x －3)2＋y 2＝64，求动圆圆心M 的轨迹方程．解：设动圆M 的半径为r ，则|MA |＝r ，|MB |＝8－r ，∴|MA |＋|MB |＝8，且8>|AB |＝6，∴动点M 的轨迹是椭圆，且焦点分别是A (－3，0)，B (3，0)，且2a ＝8，∴a ＝4，c ＝3，∴b 2＝a 2－c 2＝16－9＝7.∴所求动圆圆心M 的轨迹方程是x 216＋y 27＝1.13．已知椭圆的长轴长为10，两焦点F 1，F 2的坐标分别为(3，0)和(－3，0)．(1)求椭圆的标准方程；(2)若P 为短轴的一个端点，求△F 1PF 2的面积．解：(1)设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)， 依题意得⎩⎪⎨⎪⎧2a ＝10，c ＝3，因此a ＝5，b ＝4， 所以椭圆的标准方程为x 225＋y 216＝1. (2)易知|y P |＝4，又c ＝3，所以S △F 1PF 2＝12|y P |×2c ＝12×4×6＝12. 14．设F 1，F 2分别是椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，M 是C 上一点且MF 2与x 轴垂直，直线MF 1与C 的另一个交点为N .(1)若直线MN 的斜率为34，求C 的离心率； (2)若直线MN 在y 轴上的截距为2，且|MN |＝5|F 1N |，求a ，b .解：(1)根据c ＝a 2－b 2及题设知M ⎝⎛⎭⎫c ，b 2a ，b 2a 2c ＝34， 2b 2＝3ac .将b 2＝a 2－c 2代入2b 2＝3ac ，解得c a ＝12，c a＝－2(舍去)． 故C 的离心率为12. (2)由题意，原点O 为F 1F 2的中点，MF 2∥y 轴， 所以直线MF 1与y 轴的交点D (0，2)是线段MF 1的中点， 故b 2a＝4，即b 2＝4a .① 由|MN |＝5|F 1N |得|DF 1|＝2|F 1N |.设N (x 1，y 1)，由题意知y 1<0，则⎩⎪⎨⎪⎧2（－c －x 1）＝c ，－2y 1＝2，即⎩⎪⎨⎪⎧x 1＝－32c ，y 1＝－1.代入C 的方程，得9c 24a 2＋1b 2＝1.② 将①及c ＝a 2－b 2代入②得9（a 2－4a ）4a 2＋14a ＝1. 解得a ＝7，b 2＝4a ＝28，故a ＝7，b ＝27.14．如图，椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，过F 2的直线交椭圆于P ，Q 两点，且PQ ⊥PF 1.(1)若|PF 1|＝2＋2，|PF 2|＝2－2，求椭圆的标准方程；(2)若|PQ |＝λ|PF 1|，且34≤λ<43，试确定椭圆离心率e 的取值范围．解：(1)由椭圆的定义知，2a ＝|PF 1|＋|PF 2|＝(2＋2)＋(2－2)＝4，故a ＝2. 设椭圆的半焦距为c ，由已知得PF 1⊥PF 2， 因此2c ＝|F 1F 2|＝|PF 1|2＋|PF 2|2 ＝(2＋2)2＋(2－2)2＝23，即c ＝3，从而b ＝a 2－c 2＝1.故所求椭圆的标准方程为x 24＋y 2＝1. (2)如图，由PF 1⊥PQ ，|PQ |＝λ|PF 1|，得|QF 1|＝|PF 1|2＋|PQ |2＝1＋λ2|PF 1|.由椭圆的定义知，|PF 1|＋|PF 2|＝2a ，|QF 1|＋|QF 2|＝2a ，所以|PF 1|＋|PQ |＋|QF 1|＝4a .于是(1＋λ＋1＋λ2)|PF 1|＝4a ，解得|PF 1|＝4a 1＋λ＋1＋λ2， 故|PF 2|＝2a －|PF 1|＝2a (λ＋1＋λ2－1)1＋λ＋1＋λ2. 由勾股定理得|PF 1|2＋|PF 2|2＝|F 1F 2|2＝(2c )2＝4c 2，从而⎝ ⎛⎭⎪⎫4a 1＋λ＋1＋λ22＋⎣⎢⎡⎦⎥⎤2a (λ＋1＋λ2－1)1＋λ＋1＋λ22＝4c 2， 两边除以4a 2，得4(1＋λ＋1＋λ2)2＋(λ＋1＋λ2－1)2(1＋λ＋1＋λ2)2＝e 2. 若记t ＝1＋λ＋1＋λ2，则上式变成e 2＝4＋(t －2)2t 2＝8⎝⎛⎭⎫1t －142＋12. 由34≤λ<43及1＋λ＋1＋λ2关于λ的单调性， 得3≤t <4，即14<1t ≤13，进而12<e 2≤59，即22<e ≤53.。

椭圆的焦点性质
1 焦距定理
椭圆上任意一点到两个焦点的距离之和等于长轴的长度。
2 焦点到直线的距离
椭圆上任意一点到直线的距离与其与两个焦点的距离相等。
3 焦点到任一点距离之和
焦点到椭圆上任意一点距离之和等于长轴的长度。
椭圆的切线
1
切点和法线垂直于切线。
2
切线的斜率和方程
总结
1 椭圆的定义及特点
椭圆是由两个焦点和常距 离点的连线构成的几何形 态。
2 椭圆的焦点、切线和
双曲线性质
椭圆具有焦点性质，切线 和双曲线也与椭圆有所关 联。
3 椭圆的应用和意义
椭圆在工程、艺术和日常 生活中扮演着重要的角色， 具有广泛的应用和意义。
切线的斜率可以通过椭圆的参数表示，方程可以通过切点和斜率求得。
3
切线和弦的交点和中垂线
切线和椭圆上任意一条弦的交点在椭圆的中垂线上。
椭圆的双曲线性质
椭圆与双曲线的区别
椭圆的焦点在内部，离心率小 于1；双曲线的焦点在外部，离 心率大于1。
双曲线的基本形态
双曲线具有两个分离的曲线臂， 曲线臂的形状类似于打开的喇 叭。
双曲线的焦点和离心 率
双曲线也有焦点和离心率的概 念，但与椭圆略有不同。
椭圆的应用
椭圆在工程中的应用
椭圆在艺术中的运用
椭圆形状可以应用于桥梁设计， 提供更好的结构支持和负载分散。
椭圆形状在艺术作品中常用于创 造平衡、和谐和美感的效果。
椭圆在日常生活中的例子
行星轨道、椭圆形家具等都是椭 圆在日常生活中的例子。
《椭圆的几何性质》PPT 课件
欢迎来到《椭圆的几何性质》PPT课件！在本课程中，我们将深入研究椭圆的 几何性质，涵盖定义、基本形态、焦点性质、切线、双曲线性质、应用等内 容。让我们一起开始这个精彩的学习之旅吧。

椭圆的简单几何性质教案（实用版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的实用资料，如工作总结、工作报告、文案策划、工作计划、讲话致辞、合同模板、教案大全、作文大全、心得体会、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of practical materials for everyone, such as work summaries, work reports, copywriting plans, work plans, speeches, contract templates, lesson plans, essays, experiences, and other materials. If you want to learn about different data formats and writing methods, please pay attention!椭圆的简单几何性质教案椭圆的简单几何性质教案主要包括以下内容：一、教学目标：1.熟悉椭圆的几何性质，如对称性、范围、顶点、离心率等。

椭圆的概念与几何性质一、知识梳理1.椭圆的定义在平面内与两定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距.其数学表达式：集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a＞0，c＞0，且a，c为常数：(1)若a＞c，则集合P为椭圆；(2)若a＝c，则集合P为线段；(3)若a＜c，则集合P为空集.2.椭圆的标准方程和几何性质a b a b3、点P(x0，y0)和椭圆的位置关系(1)点P(x0，y0)在椭圆内⇔x20a2＋y20b2<1；(2)点P(x0，y0)在椭圆上⇔x20a2＋y20b2＝1；(3)点P(x0，y0)在椭圆外⇔x20a2＋y20b2>1.二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”)(1)平面内与两个定点F1，F2的距离之和等于常数的点的轨迹是椭圆.()(2)椭圆的离心率e越大，椭圆就越圆.()(3)方程mx2＋ny2＝1(m>0，n>0，m≠n)表示的曲线是椭圆.()(4)x2a2＋y2b2＝1(a>b>0)与y2a2＋x2b2＝1(a>b>0)的焦距相同.()解析(1)由椭圆的定义知，当该常数大于|F1F2|时，其轨迹才是椭圆，而常数等于|F1F2|时，其轨迹为线段F1F2，常数小于|F1F2|时，不存在这样的图形.(2)因为e＝ca＝a2－b2a＝1－⎝⎛⎭⎪⎫ba2，所以e越大，则ba越小，椭圆就越扁.答案(1)×(2)×(3)√(4)√2.若F1(3，0)，F2(－3，0)，点P到F1，F2的距离之和为10，则P点的轨迹方程是________.解析因为|PF1|＋|PF2|＝10>|F1F2|＝6，所以点P的轨迹是以F1，F2为焦点的椭圆，其中a＝5，c＝3，b＝a2－c2＝4，故点P的轨迹方程为x225＋y216＝1.答案x225＋y216＝13.已知点P是椭圆x25＋y24＝1上y轴右侧的一点，且以点P及焦点F1，F2为顶点的三角形的面积等于1，则点P的坐标为________.解析设P(x，y)，由题意知c2＝a2－b2＝5－4＝1，所以c＝1，则F1(－1，0)，F2(1，0)，由题意可得点P到x轴的距离为1，所以y＝±1，把y＝±1代入x25＋y24＝1，得x＝±152，又x＞0，所以x＝152，∴P点坐标为(152，1)或(152，－1). 答案(152，1)或(152，－1)4.(2018·张家口调研)椭圆x 216＋y 225＝1的焦点坐标为( ) A.(±3，0)B.(0，±3)C.(±9，0)D.(0，±9)解析 根据椭圆方程可得焦点在y 轴上，且c 2＝a 2－b 2＝25－16＝9，∴c ＝3，故焦点坐标为(0，±3). 答案 B5.(2018·全国Ⅰ卷)已知椭圆C ：x 2a 2＋y 24＝1的一个焦点为(2，0)，则C 的离心率为( ) A.13B.12C.22D.223解析 不妨设a >0.因为椭圆C 的一个焦点为(2，0)，所以焦点在x 轴上，且c ＝2，所以a 2＝4＋4＝8，所以a ＝22，所以椭圆C 的离心率e ＝c a ＝22. 答案 C6.(2018·武汉模拟)曲线x 225＋y 29＝1与曲线x 225－k ＋y 29－k ＝1(k <9)的( )A.长轴长相等B.短轴长相等C.离心率相等D.焦距相等解析 曲线x 225＋y 29＝1表示焦点在x 轴上的椭圆，其长轴长为10，短轴长为6，焦距为8，离心率为45.曲线x 225－k ＋y 29－k ＝1(k <9)表示焦点在x 轴上的椭圆，其长轴长为225－k ，短轴长为29－k ，焦距为8，离心率为425－k.对照选项，知D 正确. 答案 D考点一 椭圆的定义及其应用【例1】 (1)如图，圆O 的半径为定长r ，A 是圆O 内一个定点，P 是圆上任意一点，线段AP 的垂直平分线l 和半径OP 相交于点Q ，当点P 在圆上运动时，点Q 的轨迹是( )A.椭圆B.双曲线C.抛物线D.圆(2)(2018·德阳模拟)设P 为椭圆C ：x 249＋y 224＝1上一点，F 1，F 2分别是椭圆C 的左、右焦点，且△PF 1F 2的重心为点G ，若|PF 1|∶|PF 2|＝3∶4，那么△GPF 1的面积为( ) A.24B.12C.8D.6解析 (1)连接QA .由已知得|QA |＝|QP |. 所以|QO |＋|QA |＝|QO |＋|QP |＝|OP |＝r .又因为点A 在圆内，所以|OA |＜|OP |，根据椭圆的定义，点Q 的轨迹是以O ，A 为焦点，r 为长轴长的椭圆.(2)∵P 为椭圆C ：x 249＋y 224＝1上一点，|PF 1|∶|PF 2|＝3∶4，|PF 1|＋|PF 2|＝2a ＝14，∴|PF 1|＝6，|PF 2|＝8，又∵|F 1F 2|＝2c ＝249－24＝10，∴易知△PF 1F 2是直角三角形，S △PF 1F 2＝12|PF 1|·|PF 2|＝24，∵△PF 1F 2的重心为点G ，∴S △PF 1F 2＝3S △GPF 1，∴△GPF 1的面积为8. 答案 (1)A (2)C 规律方法 (1)椭圆定义的应用主要有：判断平面内动点的轨迹是否为椭圆，求焦点三角形的周长、面积及弦长、最值和离心率等.(2)通常定义和余弦定理结合使用，求解关于焦点三角形的周长和面积问题.【训练1】 (1)(2018·福建四校联考)已知△ABC 的顶点B ，C 在椭圆x 23＋y 2＝1上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC 边上，则△ABC 的周长是( ) A.2 3B.6C.4 3D.2(2)(2018·衡水中学调研)设F 1，F 2分别是椭圆x 225＋y 216＝1的左、右焦点，P 为椭圆上任意一点，点M 的坐标为(6，4)，则|PM |－|PF 1|的最小值为________. 解析 (1)由椭圆的方程得a ＝ 3.设椭圆的另一个焦点为F ，则由椭圆的定义得|BA |＋|BF |＝|CA |＋|CF |＝2a ，所以△ABC 的周长为|BA |＋|BC |＋|CA |＝|BA |＋|BF |＋|CF |＋|CA |＝(|BA |＋|BF |)＋(|CF |＋|CA |)＝2a ＋2a ＝4a ＝4 3.(2)由椭圆的方程可知F 2(3，0)，由椭圆的定义可得|PF 1|＝2a －|PF 2|，∴|PM |－|PF 1|＝|PM |－(2a －|PF 2|)＝|PM |＋|PF 2|－2a ≥|MF 2|－2a ，当且仅当M ，P ，F 2三点共线时取得等号，又|MF 2|＝（6－3）2＋（4－0）2＝5，2a ＝10，∴|PM |－|PF 1|≥5－10＝－5，即|PM |－|PF 1|的最小值为－5. 答案 (1)C (2)－5考点二 椭圆的标准方程【例2】 (1)已知两圆C 1：(x －4)2＋y 2＝169，C 2：(x ＋4)2＋y 2＝9，动圆在圆C 1内部且和圆C 1相内切，和圆C 2相外切，则动圆圆心M 的轨迹方程为( ) A.x 264－y 248＝1 B.x 248＋y 264＝1 C.x 248－y 264＝1D.x 264＋y 248＝1(2)若椭圆经过两点(2，0)和(0，1)，则椭圆的标准方程为________________. 解析 (1)设圆M 的半径为r ，则|MC 1|＋|MC 2|＝(13－r )＋(3＋r )＝16>8＝|C 1C 2|， 所以M 的轨迹是以C 1，C 2为焦点的椭圆，且2a ＝16，2c ＝8，所以a ＝8，c ＝4，b ＝a 2－b 2＝82－42＝48＝43，故所求的轨迹方程为x 264＋y 248＝1.(2)法一 当椭圆的焦点在x 轴上时，设所求椭圆的方程为x 2a 2＋y 2b 2＝1 (a >b >0).∵椭圆经过两点(2，0)，(0，1)， ∴⎩⎪⎨⎪⎧4a 2＋0b 2＝1，0a 2＋1b 2＝1，解得⎩⎨⎧a ＝2，b ＝1.∴所求椭圆的标准方程为x 24＋y 2＝1；当椭圆的焦点在y 轴上时，设所求椭圆的方程为y 2a 2＋x 2b 2＝1 (a >b >0). ∵椭圆经过两点(2，0)，(0，1)， ∴⎩⎪⎨⎪⎧0a 2＋4b 2＝1，1a 2＋0b 2＝1，解得⎩⎨⎧a ＝1，b ＝2，与a >b 矛盾，故舍去.综上可知，所求椭圆的标准方程为x 24＋y 2＝1. 法二 设椭圆方程为mx 2＋ny 2＝1 (m >0，n >0，m ≠n ).∵椭圆过(2，0)和(0，1)两点，∴⎩⎨⎧4m ＝1，n ＝1， 解得⎩⎪⎨⎪⎧m ＝14，n ＝1.综上可知，所求椭圆的标准方程为x 24＋y 2＝1. 答案 (1)D (2)x 24＋y 2＝1规律方法 根据条件求椭圆方程的主要方法有：(1)定义法：根据题目所给条件确定动点的轨迹满足椭圆的定义.(2)待定系数法：根据题目所给的条件确定椭圆中的a ，b .当不知焦点在哪一个坐标轴上时，一般可设所求椭圆的方程为mx 2＋ny 2＝1(m >0，n >0，m ≠n )，不必考虑焦点位置，用待定系数法求出m ，n 的值即可.【训练2】 (1)(2018·济南模拟)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)，若长轴长为6，且两焦点恰好将长轴三等分，则此椭圆的标准方程为( ) A.x 236＋y 232＝1 B.x 29＋y 28＝1 C.x 29＋y 25＝1D.x 216＋y 212＝1(2)(2018·榆林模拟)已知F 1(－1，0)，F 2(1，0)是椭圆C 的焦点，过F 2且垂直于x 轴的直线交椭圆C 于A ，B 两点，且|AB |＝3，则C 的方程为( ) A.x 22＋y 2＝1 B.x 23＋y 22＝1 C.x 24＋y 23＝1D.x 25＋y 24＝1解析 (1)椭圆长轴长为6，即2a ＝6，得a ＝3，∵两焦点恰好将长轴三等分， ∴2c ＝13×2a ＝2，得c ＝1， 因此，b 2＝a 2－c 2＝9－1＝8，所以此椭圆的标准方程为x 29＋y 28＝1.(2)由题意，设椭圆方程为x 2a 2＋y 2b 2＝1(a >b >0)，将A (c ，y 1)代入椭圆方程得c 2a 2＋y 21b 2＝1，由此求得y 21＝b 4a 2，所以|AB |＝3＝2b 2a ，又c ＝1，a 2－b 2＝c 2，可解得a ＝2，b 2＝3，所以椭圆C 的方程为x 24＋y 23＝1.答案 (1)B (2)C考点三 椭圆的几何性质 角度1 椭圆的长轴、短轴、焦距【例3－1】 (2018·泉州质检)已知椭圆x 2m －2＋y 210－m ＝1的长轴在x 轴上，焦距为4，则m 等于( ) A.8B.7C.6D.5解析 因为椭圆x 2m －2＋y210－m＝1的长轴在x 轴上，所以⎩⎨⎧m －2>0，10－m >0，m －2>10－m ，解得6<m <10.因为焦距为4，所以c 2＝m －2－10＋m ＝4，解得m ＝8. 答案 A角度2 椭圆的离心率【例3－2】 (2018·全国Ⅱ卷)已知F 1，F 2是椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，A 是C 的左顶点，点P 在过A 且斜率为36的直线上，△PF 1F 2为等腰三角形，∠F 1F 2P ＝120°，则C 的离心率为( ) A.23B.12C.13D.14解析 由题意可知椭圆的焦点在x 轴上，如图所示，设|F 1F 2|＝2c ，∵△PF 1F 2为等腰三角形，且∠F 1F 2P ＝120°， ∴|PF 2|＝|F 1F 2|＝2c .∵|OF 2|＝c ，过P 作PE 垂直x 轴于点E ，则∠PF 2E ＝60°，所以|F 2E |＝c ，|PE |＝3c ，即点P (2c ，3c ).∵点P 在过点A ，且斜率为36的直线上， ∴3c 2c ＋a ＝36，解得c a ＝14，∴e ＝14. 答案 D 角度3 与椭圆性质有关的最值或范围问题【例3－3】 (2017·全国Ⅰ卷)设A ，B 是椭圆C ：x 23＋y 2m ＝1长轴的两个端点.若C 上存在点M 满足∠AMB ＝120°，则m 的取值范围是( ) A.(0，1]∪[9，＋∞) B.(0，3]∪[9，＋∞) C.(0，1]∪[4，＋∞)D.(0，3]∪[4，＋∞)解析 ①当焦点在x 轴上，依题意得 0<m <3，且3m≥tan ∠AMB 2＝ 3. ∴0<m <3且m ≤1，则0<m ≤1.②当焦点在y 轴上，依题意m >3，且m3≥tan ∠AMB 2＝3，∴m ≥9，综上，m 的取值范围是(0，1]∪[9，＋∞). 答案 A规律方法 1.求椭圆离心率的方法(1)直接求出a ，c 的值，利用离心率公式直接求解.(2)列出含有a ，b ，c 的齐次方程(或不等式)，借助于b 2＝a 2－c 2消去b ，转化为含有e 的方程(或不等式)求解.2.在求与椭圆有关的一些量的范围，或者最值时，经常用到椭圆标准方程中x ，y的范围、离心率的范围等不等关系.【训练3】 (1)以椭圆上一点和两个焦点为顶点的三角形的面积的最大值为1，则椭圆长轴长的最小值为( ) A.1B. 2C.2D.22(2)(2019·豫南九校联考)已知两定点A (－1，0)和B (1，0)，动点P (x ，y )在直线l ：y ＝x ＋3上移动，椭圆C 以A ，B 为焦点且经过点P ，则椭圆C 的离心率的最大值为( ) A.55B.105C.255D.2105解析 (1)设a ，b ，c 分别为椭圆的长半轴长、短半轴长、半焦距， 依题意知，当三角形的高为b 时面积最大， 所以12×2cb ＝1，bc ＝1，而2a ＝2b 2＋c 2≥22bc ＝22(当且仅当b ＝c ＝1时取等号).即长轴长2a 的最小值为2 2.(2)不妨设椭圆方程为x 2a 2＋y 2a 2－1＝1(a >1)，与直线l 的方程联立⎩⎪⎨⎪⎧x2a 2＋y 2a 2－1＝1，y ＝x ＋3，消去y 得(2a 2－1)x 2＋6a 2x ＋10a 2－a 4＝0， 由题意易知Δ＝36a 4－4(2a 2－1)(10a 2－a 4)≥0，解得a ≥5， 所以e ＝c a ＝1a ≤55，所以e 的最大值为55. 答案 (1)D (2)A[思维升华]1.椭圆的定义揭示了椭圆的本质属性，正确理解、掌握定义是关键，应注意定义中的常数大于|F 1F 2|，避免了动点轨迹是线段或不存在的情况.2.求椭圆的标准方程，常采用“先定位，后定量”的方法(待定系数法).先“定位”，就是先确定椭圆和坐标系的相对位置，以椭圆的中心为原点的前提下，看焦点在哪条坐标轴上，确定标准方程的形式；再“定量”，就是根据已知条件，通过解方程(组)等手段，确定a 2，b 2的值，代入所设的方程，即可求出椭圆的标准方程.若不能确定焦点的位置，这时的标准方程常可设为mx 2＋ny 2＝1(m ＞0，n ＞0且m ≠n )三、课后练习1.已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左顶点为M ，上顶点为N ，右焦点为F ，若NM →·NF →＝0，则椭圆的离心率为( ) A.32B.2－12C.3－12D.5－12解析 由题意知，M (－a ，0)，N (0，b )，F (c ，0)，∴NM→＝(－a ，－b )，NF →＝(c ，－b ).∵NM →·NF →＝0，∴－ac ＋b 2＝0，即b 2＝ac .又b 2＝a 2－c 2，∴a 2－c 2＝ac .∴e 2＋e －1＝0，解得e ＝5－12或e ＝－5－12(舍).∴椭圆的离心率为5－12.答案 D2.(2019·湖南湘东五校联考)已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，P 是椭圆上一点，△PF 1F 2是以F 2P 为底边的等腰三角形，且60°<∠PF 1F 2<120°，则该椭圆的离心率的取值范围是( ) A.(3－12，1)B.(3－12，12)C.⎝ ⎛⎭⎪⎫12，1D.⎝ ⎛⎭⎪⎫0，12 解析 由题意可得，|PF 2|2＝|F 1F 2|2＋|PF 1|2－2|F 1F 2|·|PF 1|cos ∠PF 1F 2 ＝4c 2＋4c 2－2·2c ·2c ·cos ∠PF 1F 2，即|PF 2|＝22c ·1－cos ∠PF 1F 2， 所以a ＝|PF 1|＋|PF 2|2＝c ＋2c ·1－cos ∠PF 1F 2，又60°<∠PF 1F 2<120°， ∴－12<cos ∠PF 1F 2<12，所以2c <a <(3＋1)c ，则13＋1<c a <12，即3－12<e <12. 答案 B3.(2018·浙江卷)已知点P (0，1)，椭圆x 24＋y 2＝m (m >1)上两点A ，B 满足AP →＝2PB →，则当m ＝________时，点B 横坐标的绝对值最大.解析 设A (x 1，y 1)，B (x 2，y 2)，由AP→＝2PB →， 得⎩⎨⎧－x 1＝2x 2，1－y 1＝2（y 2－1），即x 1＝－2x 2，y 1＝3－2y 2.因为点A ，B 在椭圆上，所以⎩⎪⎨⎪⎧4x 224＋（3－2y 2）2＝m ，x 224＋y 22＝m ，得y 2＝14m ＋34，所以x 22＝m －(3－2y 2)2＝－14m 2＋52m －94＝－14(m －5)2＋4≤4，所以当m ＝5时，点B 横坐标的绝对值最大，最大值为2.答案 54.(2019·石家庄月考)已知点M (6，2)在椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)上，且椭圆的离心率为63.(1)求椭圆C 的方程；(2)若斜率为1的直线l 与椭圆C 交于A ，B 两点，以AB 为底边作等腰三角形，顶点为P (－3，2)，求△P AB 的面积.解 (1)由已知得⎩⎪⎨⎪⎧6a 2＋2b 2＝1，c a ＝63，a 2＝b 2＋c 2，解得⎩⎨⎧a 2＝12，b 2＝4. 故椭圆C 的方程为x 212＋y 24＝1.(2)设直线l 的方程为y ＝x ＋m ，A (x 1，y 1)，B (x 2，y 2)，AB 的中点为D (x 0，y 0). 由⎩⎪⎨⎪⎧y ＝x ＋m ，x 212＋y 24＝1，消去y ，整理得4x 2＋6mx ＋3m 2－12＝0， 由根与系数的关系得x 1＋x 2＝－32m ，x 1x 2＝3m 2－124， 由Δ＝36m 2－16(3m 2－12)>0得m 2<16，则x 0＝x 1＋x 22＝－34m ，y 0＝x 0＋m ＝14m ，即D ⎝ ⎛⎭⎪⎫－34m ，14m . 因为AB 是等腰△P AB 的底边，所以PD ⊥AB ，即PD 的斜率k ＝2－m 4－3＋3m 4＝－1，解得m ＝2，满足m 2<16. 此时x 1＋x 2＝－3，x 1x 2＝0，则|AB |＝2|x 1－x 2|＝2·（x 1＋x 2）2－4x 1x 2＝32，又点P 到直线l ：x －y ＋2＝0的距离为d ＝32， 所以△P AB 的面积为S ＝12|AB |·d ＝92.5.已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的右焦点为F (1，0)，其关于直线y ＝bx 的对称点Q 在椭圆上，则离心率e ＝________，S △FOQ ＝________.解析 设点Q (x ，y )，则由点Q 与椭圆的右焦点F (1，0)关于直线y ＝bx 对称得⎩⎪⎨⎪⎧y x －1＝－1b ，y 2＝b ·x ＋12，解得⎩⎪⎨⎪⎧x ＝1－b 21＋b 2，y ＝2b 1＋b 2，代入椭圆C 的方程得（1－b 2）2a 2（1＋b 2）2＋4b 2b 2（1＋b 2）2＝1，结合a 2＝b 2＋1解得⎩⎨⎧a ＝2，b ＝1，则椭圆的离心率e ＝c a ＝22，S △FOQ ＝12 |OF |·⎪⎪⎪⎪⎪⎪2b 1＋b 2＝12×1×21＋12＝12. 答案 22 12。

椭圆的标准方程及其几何性质1. 椭圆定义：（1）第一定义：平面内与两个定点21F F 、的距离之和为常数|)|2(222F F a a >的动点P 的轨迹叫椭圆,其中两个定点21F F 、叫椭圆的焦点.当21212F F a PF PF >=+时, P 的轨迹为椭圆 ; ; 当21212F F a PF PF <=+时, P 的轨迹不存在;当21212F F a PF PF ==+时, P 的轨迹为 以21F F 、为端点的线段（2）椭圆的第二定义:平面内到定点F 与定直线l (定点F 不在定直线l 上)的距离之比是常数e (10<<e )的点的轨迹为椭圆（利用第二定义,可以实现椭圆上的动点到焦点的距离与到相应准线的距离相互转化）. 2.椭圆的方程与几何性质:3.点),(00y x P 与椭圆)0(12222>>=+b a b y a x 的位置关系:当12222>+b y a x 时,点P 在椭圆外; 当12222>+b y a x 时,点P 在椭圆内; 当12222=+b y a x 时,点P 在椭圆上; 4.直线与椭圆的位置关系直线与椭圆相交0>∆⇔;直线与椭圆相切0=∆⇔;直线与椭圆相离0<∆⇔ 例题分析：题1写出适合下列条件的椭圆的标准方程：⑴两个焦点坐标分别是(-4,0)、（4，0），椭圆上一点P 到两焦点的距离 之和等于10；⑵两个焦点坐标分别是（0，－2）和（0,2）且过（23-,25） (3)两个焦点坐标分别是(-3，0)，(3，0)，椭圆经过点(5，0).(4)两个焦点坐标分别是(0，5)，(0，-5)，椭圆上一点P 到两焦点的距离和为26. (5)焦点在y 轴上，与y 轴的一个交点为P (0，－10)，P 到它较近的一个焦点的距离等于2.解：（1）因为椭圆的焦点在x 轴上，所以设它的标准方程为所以所求椭圆标准方程为92522=+y x ⑵ 因为椭圆的焦点在y 轴上，所以设它的标准方程为由椭圆的定义知，22)225()23(2++-=a ＋22)225()23(-+-10=∴a 又2=c所以所求标准方程为61022=+x y 另法：∵ 42222-=-=a c a b∴可设所求方程142222=-+a x a y ，后将点（23-,25）的坐标代入可求出a ，从而求出椭圆方程(3)∵椭圆的焦点在x 轴上，所以设它的标准方程为： ∵100)35(0)35(222=+-+++=a ，2c =6. ∴3,5==c a∴163522222=-=-=c a b∴所求椭圆的方程为：1162522=+y x . (4)∵椭圆的焦点在y 轴上，所以设它的标准方程为)0(12222>>=+b a bx a y . ∴.144222=-=c a b∴所求椭圆方程为：114416922=+x y （5）∵椭圆的焦点在y 轴上，所以可设它的标准方程为： ∵Ｐ（０，－１０）在椭圆上，∴a ＝１０.又∵P 到它较近的一焦点的距离等于2， ∴－c －（－１０）＝２，故c =8. ∴36222=-=c a b .∴所求椭圆的标准方程是13610022=+x y . 题2。

人教版选修21第二章椭圆椭圆的几何性质讲义案例（二）——精析精练课堂合作探究重点难点突知识点 椭圆的几何性质 由椭圆方程()012222>>=+b a by a x 研究椭圆的性质。

(利用方程研究，说明结论与由图 形观察一致）（1）范围 从标准方程得出1,12222≤≤by a x ，即有b y b a x a ≤≤-≤≤-,，可知椭圆落在by a x ±=±=,组成的矩形中。

（2）对称性把方程中的x 换成x -方程不变，图象关于y 轴对称。

y 换成y -方程不变，图象关于x轴对称。

把y x ,同时换成y x ,-方程也不变，图象关于原点对称。

如果曲线具有关于x 轴对称，关于y 轴对称和关于原点对称中的任意两种，则它一定具的 ,对称性、顶点。

因而只需少量描点就可以较正确地作图了。

（3）离心率长轴相等，短轴不同，扁圆程度不同，这种扁平性质是由椭圆焦距与长轴长之比来决定的。

由于21⎪⎭⎫⎝⎛-=⇒=a b e a c e ，b a >，所以离心率的范围是10<<e 。

当0,0→→c e ,椭圆变圆，直至成为极限位置圆，此时也可认为圆为椭圆在0=e 时的特例；当a c e →→,1,椭圆变扁，直至成为极限位置线段21F F ，此时也可认为圆为椭圆在1=e 时的特例，如右图所示。

典型例题分析题型1 椭圆中几何性质的考查 【例1】 已知椭圆的方程为81922=+y x的长轴长为 ，短轴长为 ，焦点坐标为 ，顶点坐标为 ，离心率为 。

解析 先化成标准方程,再确定有关性质。

将81922=+y x化为标准方程1932222=+y x 。

∴椭圆长轴在y 轴上,其中26,3,9===c b a ， ∴长轴长182=a ,短轴长62=b ,焦点坐标为()26,01-F ，()26,02F ，顶点坐标为()0,31-A 、()0,32A 、()9,01-B 、()9,02B 。

椭圆是平面上的一个几何图形，具有一些特殊的性质。

以下是一些椭圆的几何性质：
1.定义性质：椭圆是一个点到两个焦点距离之和等于常数的点
集合。

这个常数称为椭圆的长轴长度，长轴的中点称为椭圆
的中心。

2.对称性质：椭圆具有两个对称轴，即横轴和纵轴。

横轴和纵
轴互相垂直，并交于椭圆的中心。

3.焦点性质：椭圆的焦点是椭圆的两个特殊点，对于椭圆上的
每一个点，它到两个焦点的距离之和是恒定的，等于椭圆的
长轴长度。

4.直径性质：椭圆的任意一条直径的长度等于椭圆的长轴长度。

5.切线性质：椭圆上的每一条切线与椭圆的两个焦点之间的线
段的长度是相等的。

6.圆锥截面性质：椭圆是一个旋转椭圆曲线，可以通过将一个
圆沿一个不在圆心处的直线截成椭圆来得到。

这些性质为椭圆的研究和应用提供了基础，例如在数学、物理、工程等领域中，椭圆的性质被广泛应用于解决实际问题。

练习：课本41页1，2，3, 4
学生活动(课本41页练习1)
思考:已知椭圆的长轴A1A2和短轴B1B2 ，
怎样确定椭圆焦点的位置？
B2
a
A1
F1 c
b
oc
a
A2
F2
因为a2=b2+c2,所以以椭圆B1 短轴端点为 圆心,a长为半径的圆与x轴的交点即为 椭圆焦点.
y
例5 如图2.1 11,一种
则原方程组有两组解. 所以该直线与椭圆相交.
变式1：交点坐标是什么？
A(1, 1), B( 2
变式2：相交所得的弦的弦长是多少？
1, 7 ) 5 10 | AB |
6 5
5
弦长公式：| AB | 1 k2 x1 x2 1 k2 （x1 x2 )2 4x1x2
k表示弦的斜率，x1、x2表示弦的端点坐标
(3)弦长公式： 设直线方程为 y＝kx＋m(k≠0)，椭圆方程为ax22＋yb22＝1(a>b>0)或 ya22＋bx22＝1(a>b>0)，直线与椭圆的两个交点为 A(x1，y1)，B(x2， y2)，则|AB|＝ （x1－x2）2＋（y1－y2）2，
∴|AB|＝ （x1－x2）2＋（kx1－kx2）2
上是否存在一点,到直线 l 的距离最小?最小距离是多少?
分析:设 P( x0 , y0 ) 是椭圆上任一点, 试求点 P 到直线 4x 5 y 40 0的距离的表达式.
d 4x0 5 y0 40 4x0 5 y0 40
y A1
F1 O
F2
x
A2
椭圆关于原点对称。
2、椭圆的对称性
x2
y2
a 2 b2 1(a b 0)