8-5直接由平衡条件建立位移法基本方程
- 格式:ppt
- 大小:1.31 MB
- 文档页数:27


第8章 位移法(知识点小结)一、杆端内力正负号规定(图8-1)杆端弯矩AB M 、BA M :以绕杆端顺时针为正,逆时针为负;对结点或支座而言,截面弯矩以逆时针为正。
杆端剪力SAB F 、SBA F :以绕微段隔离体顺时针转动者为正,反之为负。
结点转角(杆端转角)A θ、B θ:顺时针转动为正。
两端垂直杆轴的相对线位移AB ∆:以使杆件顺时针转动为正,反之为负。
图8-1 杆端内力及杆端位移的正负号规定二、等截面直杆的转角位移方程—位移法计算的基础1、由杆端位移求杆端力——形常数考虑三种不同情况:两端固定直杆、一端固定另一端铰支的直杆及一端固定另一端滑动支承的直杆。
由杆端位移求杆端内力的公式(刚度方程),如表8-1所示,这里/i EI l =。
由杆端位移求出杆端弯矩后,杆端剪力可由平衡条件求出。
表8-1中,杆端内力是根据图示方向的位移方向求得的,当计算某一结构时,应根据其杆件所受的实际位移方向,判断其杆端内力的正负号及受拉侧。
2、由荷载求固定内力——载常数对三种等截面直杆,在荷载作用、温度改变作用下的杆端弯矩和剪力,称为固端弯矩和固端剪力(载常数)。
常见荷载作用下的载常数可查表所得。
3、等截面直杆的转角位移方程对等截面直杆,既有已知荷载作用,又有已知的杆端位移,可根据叠加原理,写出其杆端力的一般表达式,这即为等截面直杆的转角位移方程。
三、位移法的基本未知量包括独立的结点角位移和独立的结点线位移。
独立的结点角位移数目等于刚结点(包括组合结点、弹性抗转弹簧)的数目。
结点线位移的数目可通过增设支杆法(或铰化体系法)来确定。
铰化体系法就是将原结构中所有刚结点和固定支座均改为铰结点形成铰接体系,此铰接体系的自由度数就是原结构的独立结点线位移数。
然后分析该铰接体系的几何组成:如果它是几何不变的,说明结构无结点线位移;相反,如果铰接体系是几何可变的,再看最少需要增设几根附加支杆才能确保体系成为几何不变,或者说使此铰接体系成为几何不变而需添加的最少支杆数就等于原结构的独立结点线位移数目。




第8章 位移法§8-1 概述§8-2 等截面直杆的转角位移方程§8-3 位移法的基本未知量和基本结构§8-4 位移法的典型方程及计算步骤§8-5 直接由平衡条件建立位移法基本方程§8-6 对称性的应用2021-5-1212021-5-12 1§8-1 位移法的基本概念内力对于线弹性结构位移位移内力两种方法的基本区别之一,在于基本未知量的选取不同:力法是以多余未知力(支反力或内力)为基本未知量,而位移法则是以结点的独立位移(角位移或线位移)为基本未知量。
用位移法分析结构时,先将结构拆分成单个的杆件,进行杆件受力分析(建立杆件的转角位移方程);再将杆件组装成原结构,利用结点和截面平衡条件建立位移法方程,解出结点位移,再由转角位移方程求出内力。
2021-5-121一、引例1. 确定基本位移未知量图a所示两跨常刚度连续梁,抗弯刚度为EI。
忽略二杆的轴向变形,B结点不会发生线位移,而仅会产生角位移,设此角位移为Z1。
因B结点刚结两梁段于B端,从而保证两梁段在B端有相同的角位移,均为Z1。
2021-5-1212. 分列各组成杆的转角位移方程AB和BC二杆在B端具有相同的角位移和零线位移后,因此可将二杆在B端处分开,单独分析。
2021-5-1211)AB杆2)BC杆2021-5-1213. 通过B结点的平衡条件求出Z1由B结点的平衡可得2021-5-1214. 将Z1代回转角位移方程,求出各杆端弯矩2021-5-1212021-5-121二、其他示例(a) 若略去受弯直杆的轴向变形,并不计由于弯曲而引起杆段两端的接近,则可认为三杆长度不变,因而结点A没有线位移,而只有角位移。
对整个结构来说,求解的关键就是如何确定基本未知量q A的值。
2021-5-1212021-5-121三、位移法计算原理思路小结1. 把结构在非支座结点处拆开,将各杆视为相应的单跨超静定梁。
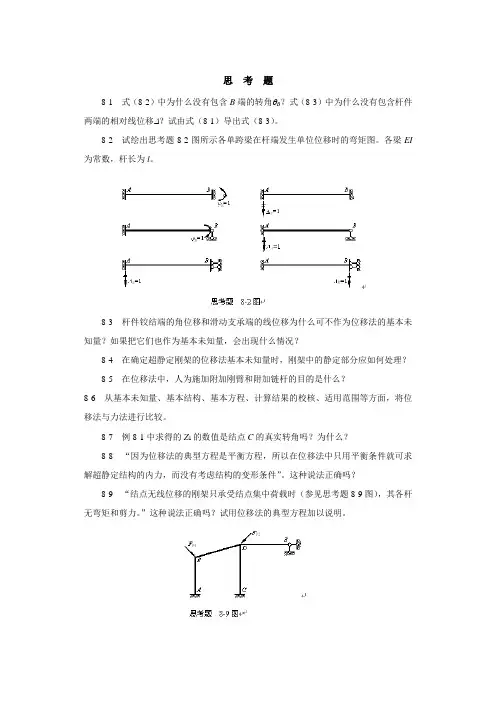
思考题8-1式(8-2)中为什么没有包含B端的转角θB?式(8-3)中为什么没有包含杆件两端的相对线位移∆?试由式(8-1)导出式(8-3)。
8-2试绘出思考题8-2图所示各单跨梁在杆端发生单位位移时的弯矩图。
各梁EI 为常数,杆长为l。
8-3杆件铰结端的角位移和滑动支承端的线位移为什么可不作为位移法的基本未知量?如果把它们也作为基本未知量,会出现什么情况?8-4在确定超静定刚架的位移法基本未知量时,刚架中的静定部分应如何处理?8-5在位移法中,人为施加附加刚臂和附加链杆的目的是什么?8-6从基本未知量、基本结构、基本方程、计算结果的校核、适用范围等方面,将位移法与力法进行比较。
8-7例8-1中求得的Z1的数值是结点C的真实转角吗?为什么?8-8“因为位移法的典型方程是平衡方程,所以在位移法中只用平衡条件就可求解超静定结构的内力,而没有考虑结构的变形条件”。
这种说法正确吗?8-9“结点无线位移的刚架只承受结点集中荷载时(参见思考题8-9图),其各杆无弯矩和剪力。
”这种说法正确吗?试用位移法的典型方程加以说明。
8-10 用力法计算思考题8-10图a所示超敬定结构,若取图b所示超静定的基本体系,是否可行?a) b)8-11 思考题8-11图a、b所示两结构的EI相同,试分别写出其位移法方程,并求出方程中的系数和自由项。
8-12 思考题8-12图所示排架,考虑横梁的轴向变形(EA≠∞)和不考虑横梁的轴向变形(EA=∞),柱的内力有什么不同?8-13 试推导思考题8-13图所示刚架柱的侧移刚度系数(柱两端发生单位相对侧移时,柱中产生的剪力值。
),用剪力分配法求出各柱柱高中点处的剪力并作出弯矩图。
8-14 思考题8-14图所示三种结构的各杆长均为l,柱的EI=常数。
试分析它们的内力及柱顶侧移的差别?。


