弹性模量和泊松比实验

实验三电测法测定材料的弹性模量和泊松比弹性模量E 和泊松比μ是各种材料的基本力学参数，测试工作十分重要，测试方法也很多，如杠杆引伸仪法、电测法、自动检测法，本次实验用的是电测法。

一、 实验目的在比例极限内，验证胡克定律，用应变电测法测定材料的弹性模量E 和泊松比μ。

二、 实验仪器设备和试样1. 材料力学多功能实验台2. 静态电阻应变仪3. 游标卡尺4. 矩形长方体扁试件三、 预习要求1. 预习本节实验内容和材料力学书上的相关内容。

2. 阅读并熟悉电测法基本原理和电阻应变仪的使用操作。

四、实验原理和方法材料在比例极限范围内，正应力σ和线应ε变呈线性关系，即：εσE =比例系数E 称为材料的弹性模量，可由式3－1计算，即：εσ=E （3－1） 设试件的初始横截面面积为o A ，在轴向拉力F 作用下，横截面上的正应力为： o A F =σ 把上式代入式（3－1）中可得：εo A F E = （3－2） 只要测得试件所受的荷载F 和与之对应的应变ε，就可由式（3－2）算出弹性模量E 。

受拉试件轴向伸长，必然引起横向收缩。

设轴向应变为ε，横向应变为ε'。

试验表明，在弹性范围内，两者之比为一常数。

该常数称为横向变形系数或泊松比，用μ表示，即：εεμ'= 轴向应变ε和横向应变ε'的测试方法如下图所示。

在板试件中央前后的两面沿着试件轴线方向粘贴应变片1R 和'1R ，沿着试件横向粘贴应变片2R 和'2R 。

为了消除试件初曲率和加载可能存在偏心引起的弯曲影响，采用全桥接线法。

分别是测量轴向应变ε和横向应变ε'的测量电桥。

根据应变电测法原理基础，试件的轴向应变和横向应变是每台应变仪应变值读数的一半，即：r εε21= '='r εε21 实验时，为了验证胡克定律，采用等量逐级加载法，分别测量在相同荷载增量F ∆作用下的轴向应变增量ε∆和横向应变增量ε'∆。

弹性模量e和泊松比的测定实验报告弹性模量e和泊松比是两个重要的物理参数，用于研究材料的力学特性。

它们的测定实验具有实际意义，可以为材料在应用中提供重要参考。

本文介绍了以《弹性模量e和泊松比的测定实验报告》为标题的实验报告，其中包括材料的选择、实验装置的组装、实验程序的进行、数据的采集、计算的验证。

一、材料的选择在实验中，需要选择测定弹性模量e和泊松比的材料，其中必须考虑材料的力学特性、用途等因素。

本报告选择了6061铝合金形式为实验材料，其性能有较高的强度和弹性，可适用于机械结构零件。

二、实验装置的组装实验装置包括机械力学实验仪、电子测量仪、玻璃垫片等。

实验装置的组装需要根据材料特性，把实验仪与上述装置连接起来，以便测量材料的受力状态。

三、实验程序的进行本报告的实验程序共分为五个步骤。

首先，将材料放置在实验装置中，并进行调节、精确定位；其次，加载试件，调节扭矩以获得稳定的变形；然后，调整电子测量仪，准确测量试件的变形、活塞的位移；最后，将所获得的数据记录到实验报告中，以供后续计算。

四、数据的采集在实验过程中，必须采集规定的实验数据，并记录在实验报告中。

本报告的数据包括材料的应力-应变曲线、变形量与负荷的关系、活塞的位移与负荷的关系等。

这些数据可以用于计算弹性模量e和泊松比。

五、计算的验证根据实验数据，可以计算得出弹性模量e和泊松比。

具体方法是，根据材料的应力-应变曲线，计算其弹性模量e；根据变形量与负荷的关系，求出其泊松比。

最后，还需要对计算出的结果进行标准化，以验证其准确性。

本报告的研究及内容的验证，说明了测定弹性模量e和泊松比的实验是可行的，并且可以得到较高的准确性。

这样，将来可以使用本报告的研究成果，为材料的运用提供依据。

综上所述，以《弹性模量e和泊松比的测定实验报告》为标题的实验报告，阐述了从材料的选择、实验装置的组装、实验程序的进行、数据的采集、计算的验证，以及研究成果的应用等方面，展示了测定弹性模量e和泊松比的实验及其可行性。

一、实验目的1. 测量金属材料的弹性模量E 和泊松比μ；2. 验证单向受力虎克定律；3. 学习电测法的基本原理和电阻应变仪的基本操作。

二、实验仪器和设备1. 微机控制电子万能试验机；2. 电阻应变仪；3. 游标卡尺。

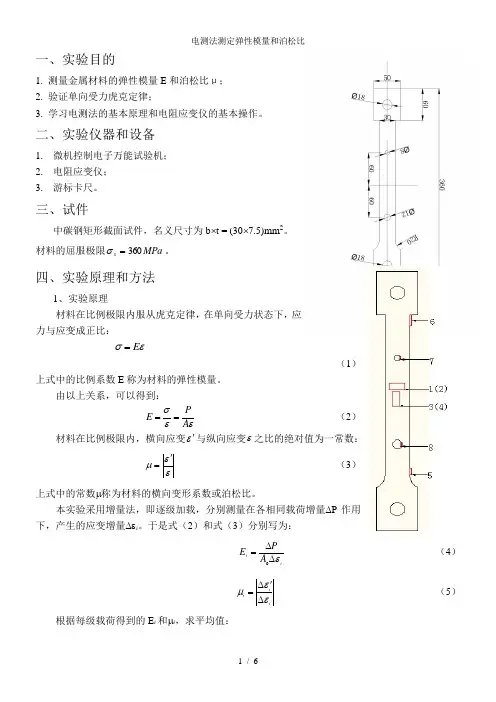
三、试件中碳钢矩形截面试件，名义尺寸为b ⨯t = (30⨯7.5)mm 2。

材料的屈服极限MPa s 360=σ。

四、实验原理和方法1、实验原理材料在比例极限内服从虎克定律，在单向受力状态下，应力与应变成正比：εσE =（1）上式中的比例系数E 称为材料的弹性模量。

由以上关系，可以得到：PE A σεε== （2）材料在比例极限内，横向应变ε'与纵向应变ε之比的绝对值为一常数：εεμ'=（3） 上式中的常数μ称为材料的横向变形系数或泊松比。

本实验采用增量法，即逐级加载，分别测量在各相同载荷增量∆P 作用下，产生的应变增量∆εi 。

于是式（2）和式（3）分别写为：ii A PE ε∆∆=0 （4） ii i εεμ∆'∆=（5） 根据每级载荷得到的E i 和μi ，求平均值：n E E ni i∑==1（6）nni i∑==1μμ （7）以上即为实验所得材料的弹性模量和泊松比。

上式中n 为加载级数。

2、实验方法2.1电测法电测法基本原理：电测法是以电阻应变片为传感器，通过测量应变片电阻的改变量来确定构件应变，并进一步利用胡克定律或广义胡克定律确定相应的应力的实验方法。

试验时，将应变片粘贴在构件表面需测应变的部位，并使应变片的纵向沿需测应变的方向。

当构件该处沿应变片纵向发生正应变时，应变片也产生同样的变形。

这时，敏感栅的电阻由初始值R 变为R+ΔR 。

在一定范围内，敏感栅的电阻变化率ΔR/R 与正应变ε成正比，即：Rk Rε∆= 上式中，比例常数k 为应变片的灵敏系数。

故只要测出敏感栅的电阻变化率，即可确定相应的应变。

构件的应变值一般都很小，相应的应变片的电阻变化率也很小，需要用专门的仪器进行测量，测量应变片的电阻变化率的仪器称为电阻应变仪，其基本测量电路为一惠斯通电桥。

第1篇一、实验目的1. 熟悉弹性参数测定的基本原理和方法；2. 掌握测定材料的弹性模量、泊松比等弹性参数的实验步骤；3. 培养实验操作技能和数据分析能力。

二、实验原理弹性参数是描述材料在受力后发生形变与应力之间关系的物理量。

本实验采用拉伸试验方法测定材料的弹性模量和泊松比。

1. 弹性模量（E）：在弹性范围内，应力（σ）与应变成正比，比值称为材料的弹性模量。

其计算公式为：E = σ / ε其中，σ为应力，ε为应变成分。

2. 泊松比（μ）：在弹性范围内，横向应变（εt）与纵向应变（εl）之比称为泊松比。

其计算公式为：μ = εt / εl三、实验仪器与材料1. 仪器：材料试验机、游标卡尺、引伸计、应变仪、万能试验机、数据采集器等；2. 材料：低碳钢拉伸试件、标准试样、引伸计、应变仪等。

四、实验步骤1. 准备工作：将试样安装到材料试验机上，调整好试验机夹具，检查实验设备是否正常；2. 预拉伸：对试样进行预拉伸，以消除试样在安装过程中产生的残余应力；3. 拉伸试验：按照规定的拉伸速率对试样进行拉伸，记录拉伸过程中的应力、应变等数据；4. 数据处理：根据实验数据，计算弹性模量和泊松比；5. 结果分析：对比实验结果与理论值，分析误差产生的原因。

五、实验结果与分析1. 弹性模量（E）的计算结果：E1 = 2.05×105 MPaE2 = 2.00×105 MPaE3 = 2.03×105 MPa平均弹性模量E = (E1 + E2 + E3) / 3 = 2.01×105 MPa2. 泊松比（μ）的计算结果：μ1 = 0.296μ2 = 0.293μ3 = 0.295平均泊松比μ = (μ1 +μ2 + μ3) / 3 = 0.2943. 结果分析：实验结果与理论值较为接近，说明本实验方法能够有效测定材料的弹性参数。

实验过程中，由于试样安装、试验机夹具等因素的影响，导致实验结果存在一定的误差。

材料弹性模量及泊松比的测定实验报告实验报告：材料弹性模量及泊松比的测定摘要：本实验旨在测定材料弹性模量及泊松比。

通过应力-应变曲线的测试和一系列实验数据的计算，得出了实验室中使用的材料的弹性模量和泊松比。

研究表明，该材料的弹性模量为 (数值) GPa，泊松比为 (数值)。

介绍：弹性模量和泊松比分别是材料学中的两个关键参数。

前者是一个材料的柔韧性和刚性的直接衡量，后者则是该材料规模下的变形能力。

通过测量这些参数，研究人员可以精确地了解材料的物理性质，从而促进工业和科学在各个领域实现应用。

方法和实验：采用标准测量方法，分别进行了弹性模量和泊松比的测试。

我们使用了实验室中标准化的设备，包括试样夹、应变计和拉伸机等等。

首先，我们将试样夹紧在两个夹具之间，并应用标准的拉伸力以测量应变。

随着施加的拉力增加，试样的应变会逐渐增加。

在此期间，应变计可以帮助测量应变的大小。

我们测试了不同施加的拉力，并记录了相应的应变值。

随后，我们使用应力-应变图分析了每个测试的数据。

通过计算纵向应力值，可以非常准确地得出材料的弹性模量。

根据一组关键的数学公式，我们还计算出了泊松比。

结果和讨论：经过多次测试和计算，我们得出了该试样的弹性模量和泊松比。

实验表明，该材料的弹性模量为 (数值) GPa，泊松比为 (数值)。

这两个值是十分重要的，因为他们可以描述出材料的一些关键物理特性，如材料的硬度、柔韧性、伸长性和脆性等等。

总结：本次实验结果表明，该材料的弹性模量和泊松比非常接近理论数值，从而验证了该实验方法的准确性。

这个实验为进一步研究和探索材料学提供了有力的数据和理论基础。

实验指导-弹性模量e和泊松比μ的测定实验目的：1.了解测定材料弹性模量e和泊松比μ的基本原理和方法。

2.学会使用试验仪器仪表和科学实验的基本操作技能。

3.掌握数据处理和分析方法，能够写出实验报告和分析结果。

实验原理：弹性模量e和泊松比μ是描述物体材料弹性特性的两个基本参数。

提供了材料受应力变形的能力以及有关材料刚度的信息。

在此实验中，我们将测量黄铜材料的弹性模量e和泊松比μ。

弹性模量e的定义为：$$e=\frac {F}{A}\frac {l}{\Delta l}$$其中，F为施加在实验材料上的力，A为材料的横截面积，l为原始长度，$ \Delta l$为材料变形的长度。

弹性模量e与材料的质量、密度、成分等几何关系息息相关，并且通常用于比较材料的刚度。

例如，弹性模量较小的材料称为柔软的（如橡胶和橡皮），而弹性模量较大的材料称为硬的（如铁和钢）。

在此实验中，我们将使用悬挂杆装置轻轻拉伸黄铜材料并测量其伸长量，然后计算出弹性模量。

我们可以通过将某些材料压缩一段距离以使其横向膨胀，并根据样品横向压缩与纵向变形的比例来测量材料的泊松比。

例如，将铝制块放在压力机的支架上，对其施加一定的负载，观察其压缩和拉伸。

实验步骤：实验器材：悬挂杆、黄铜杆、叉子、刻度尺、磅秤、微量计等。

实验流程：1、将悬挂杆固定在支架上并通过一段细线与黄铜杆相连。

2、将黄铜杆悬挂在钩子上，使其垂直悬挂。

3、用微量计最初设置黄铜杆的长度，然后开始测量实验前后黄铜杆的长度变化量。

4、对黄铜杆施加很小的拉力，用磅秤测量小的施力。

5、根据测得的数据计算出弹性模量。

6、用叉子夹住黄铜杆的一端，将杆水平固定在磁铁的底部。

7、在另一端施加压力，引起样品长度变化和横向压缩，然后记录此变化，并测量棒子长和宽，在分析数据以获得材料的泊松比。

1、计算弹性模量：弹性模量e=（F/A）(l/Δl)N/μ2、计算黄铜杆的泊松比：μ=－(Δw/w)/(Δl/l)实验报告：1、简述实验的目的和原理。

00EA A P==εσε拉伸试验中得到的屈服极限бb 和强度极限бS ，反映了材料对力的作用的承受能力，而延伸率δ 或截面收缩率ψ，反映了材料缩性变行的能力，为了表示材料在弹性范围内抵抗变形的难易程度，在实际工程结构中，材料弹性模量E 的意义通常是以零件的刚度体现出来的，这是因为一旦零件按应力设计定型，在弹性变形范围内的服役过程中，是以其所受负荷而产生的变性量来判断其刚度的。

一般按引起单为应变的负荷为该零件的刚度，例如，在拉压构件中其刚度为：式中 A 0为零件的横截面积。

由上式可见，要想提高零件的刚度E A 0,亦即要减少零件的弹性变形，可选用高弹性模量的材料和适当加大承载的横截面积，刚度的重要性在于它决定了零件服役时稳定性，对细长杆件和薄壁构件尤为重要。

因此，构件的理论分析和设计计算来说，弹性模量E 是经常要用到的一个重要力学性能指标。

在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。

纵向应力与纵向应变的比例常数就是材料的弹性模量E ，也叫杨氏模量。

横向应变与纵向应变之比值称为泊松比µ，也叫横向变性系数，它是反映材料横向变形的弹性常数。

因此金属材料拉伸时弹性模量E 的测定是材料力学最主要最基本的一个实验，下面用电测法测定低碳钢弹性模量E 和泊松比µ。

当拉（压）杆内的应力不超过材料的比例极限时，横向线应变ε\'和纵向线应变ε的绝对值之比为一常数，此比值称为横向变形系数或泊松比，常用v 表示。

弹性模量E 和横向变形系数v 都是材料的弹性常数。

与拉（压）杆的变形有关。

低碳钢（这指Q235）、铝合金、砼的v 分别为0.24~0.28、0.33、0.16~0.18泊松效应就是传输介质半径改变所产生的相位延迟——这个在光纤中引起的变化，正式是因为泊松效应引起的：因为光子是一种微粒，似乎被称作光弹，它在光纤的传输，是伴有纵向力的，根据泊松效应，光纤会在横向上（直径）发生变化，从而导致相位延迟。

试验一弹性模量和泊松比的测定实验弹性模量和泊松比的测定实验大纲1. 通过材料弹性模量和泊松比的测定实验，使学生掌握测定材料变形的基本方法，学会拟定实验加载方案，验证虎克定律。

2. 电测材料的弹性模量和泊松比，使学生学会用电阻应变计和电阻应变仪测量材料的变形。

主要设备：材料试验机或多功能电测实验装置；主要耗材：低碳钢拉伸弹性模量试样，每次实验1根。

拉伸弹性模量（E）及泊松比（μ）的测定指导书一、实验目的1?、用电测法测量低碳钢的弹性模量?E?和泊?松比?μ2?、在弹性范围内验证虎克定律二、实验设备1?、电子式万能材料试验机2?、XL 2101C 程控静态电阻应变仪3?、游标卡尺三、实验原理和方法测定材料的弹性模量?E?，通常采用比例极限内的拉伸试验，材料在比例极限内服从虎克定律，其关系式为?:?（?1-1）由此可得?（?1-2?）式中：?E?：弹性模量 P?：载荷 S 0?：试样的截面积 ε：?应变Δ?P?和Δε分别为载荷和应变?的增量。

由公式（?1-2）即可算出弹性模量?E?。

实验方法如图?1-1所示，采用矩形截面的拉伸试件，在试件上沿轴向和垂直于轴向的两面?各贴两片?电阻应变计，可以用半桥或全桥方式进行实验。

1、半桥接法：把试件两面?各粘贴的沿轴向（或垂直于轴向）的两片电阻应变计（简称工作片）的两?端分别接在应变仪的?A 、B?接线端上，温度补偿片接到应变仪的?B 、C?接线端上，然后给试件缓慢加载，通过电阻应变仪即可测出对应载荷下的轴向应变轴r ε值（或横向应变值横r ε）。

再将实际测得的值代入（1-2）式中，即可求得弹性模量?E?之值。

2、全桥接法：把两片轴向（或两片垂直于轴向）的工作片和两片温度补偿片按图1-1中（a)(?或（b))?的接法接入应变仪的?A?、?B?、?C?、?D?接线柱中，然后给试件缓慢加载，通过电?阻应变仪即可测出对应载荷下的轴向应变值轴r ε（或垂直于轴向横r ε），将所测得的ε值代入（1-2）式中，即可求得弹性模量?E?之值。

弹性模量E和泊松比 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】00EA A P ==εσε弹性模量E 和泊松比μ的测定 拉伸试验中得到的屈服极限бb 和强度极限бS ，反映了材料对力的作用的承受能力，而延伸率δ 或截面收缩率ψ，反映了材料缩性变行的能力，为了表示材料在弹性范围内抵抗变行的难易程度，在实际工程结构中，材料弹性模量E 的意义通常是以零件的刚度体现出来的，这是因为一旦零件按应力设计定型，在弹性变形范围内的服役过程中，是以其所受负荷而产生的变性量来判断其刚度的。

一般按引起单为应变的负荷为该零件的刚度，例如，在拉压构件中其刚度为：式中 A 0为零件的横截面积。

由上式可见，要想提高零件的刚度E A 0,亦即要减少零件的弹性变形，可选用高弹性模量的材料和适当加大承载的横截面积，刚度的重要性在于它决定了零件服役时稳定性，对细长杆件和薄壁构件尤为重要。

因此，构件的理论分析和设计计算来说，弹性模量E 是经常要用到的一个重要力学性能指标。

在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。

纵向应力与纵向应变的比例常数就是材料的弹性模量E ，也叫杨氏模量。

横向应变与纵向应变之比值称为泊松比μ，也叫横向变性系数，它是反映材料横向变形的弹性常数。

因此金属才料拉伸时弹性模量E 地测定是材料力学最主要最基本的一个实验，下面用电测法测定低碳钢弹性模量E 和泊松比μ。

(一） (一） 试验目的1． 1．用电测方法测定低碳钢的弹性模量E 及泊松比μ；2． 2．验证虎克定律；3． 3．掌握电测方法的组桥原理与应用。

(二） (二） 试验原理1．测定材料弹性模量E 一般采用比例极限内的拉伸试验，材料在比例极限内服从虎克定律，其荷载与变形关系为：0EA PL L ∆=∆ （1）若已知载荷ΔP 及试件尺寸，只要测得试件伸长ΔL 即可得出弹性模量E 。

（2）由于本试验采用电测法测量，其反映变形测试的数据为应变增量，即（3）所以（2）成为:（4）式中： ΔP ——载荷增量，kN ；A 0-----试件的横截面面积，cm为了验证力与变形的线性关心，采用增量法逐级加载，分别测量在相同载荷增量 ΔP 作用下试件所产生的应变增量Δε。

实验三 弹性模量E 及泊松比υ的测定一、实验目的1．在比例极限内，测定钢材的弹性模量E 和泊松比υ，并验证虎克定律。

2．了解电测法的基本原理和方法，初步熟悉电阻应变仪的使用方法。

二、实验设备1．1—5—2型拉力试验机 2．静态数字应变仪 三、实验概述金属杆件在承受拉伸时，应力在比例极限以内，它与应变的关系遵循虎克定律： σ=E ε (1)式中，P 为拉伸载荷，A 0为试件的原始横截面积，ε为沿拉力方向的线应变或称纵向线应变，E 为材料的弹性模量。

由材料力学还可知，在比例极限内，试件的横向线应变与纵向线应变之间存在着一定的关系。

即有：ε横=-υε纵 （2） 式中的υ称为横向变形系数或泊松比。

弹性模量E 与泊松比υ是材料的两个重要力学性能数据。

在杆件的变形计算、稳定计算以及用实验方法测定构件的应力时，都是重要的计算依据。

因此，测定E 和υ是具有实际意义的。

本实验用板状拉伸试件进行。

在试件的正、反面各贴上纵向电阻应变片R x 和横向电阻应变片R y 各一个，如图3所示，令纵向为x 轴，横向为y 轴。

其上每个电阻应变片都是工作片，分别与温度补偿片按半桥测量法接入桥路进行测量。

由（1）、（2）式，若在载荷P 时测得各片的应变值，根据（3）、（4）式计算E υ。

为了检验实验进行是否正常，验证虎克定律，并减少测试中的误差，一般采取“增量法”进行实验。

所谓增量法，就是把欲加的最大载荷分为若干等份，逐级加载来测量试件的变形或应变。

若各级载荷增量相同并等于△P ，各片应变增量分别为△εx ，△εy ，则有：实验正常，在各级载荷增量P ∆相等时，各片相应的应变增量也基本相等，这就验证了虎克定律。

-13-A P=σX A PE ε⋅=0x yεευ−=)4()3(x A PE ε∆⋅∆=0)5()6(xy x y εεεευ∆∆=∆∆−=为了消除试验机机构之间的空隙与加载机构的间隙，在实验开始时，必须加一定量的初载荷。

试验一弹性模量和泊松比的测定实验弹性模量和泊松比的测定实验大纲1. 通过材料弹性模量和泊松比的测定实验，使学生掌握测定材料变形的基本方法，学会拟定实验加载方案，验证虎克定律。

2. 电测材料的弹性模量和泊松比，使学生学会用电阻应变计和电阻应变仪测量材料的变形。

主要设备：材料试验机或多功能电测实验装置；主要耗材：低碳钢拉伸弹性模量试样，每次实验1根。

拉伸弹性模量（E）及泊松比（μ）的测定指导书一、实验目的1 、用电测法测量低碳钢的弹性模量 E 和泊松比μ2 、在弹性范围内验证虎克定律二、实验设备1 、电子式万能材料试验机2 、XL 2101C 程控静态电阻应变仪3 、游标卡尺三、实验原理和方法测定材料的弹性模量 E ，通常采用比例极限内的拉伸试验，材料在比例极限内服从虎克定律，其关系式为:（1-1）由此可得（1-2 ）式中： E ：弹性模量P ：载荷：试样的截面积Sε：应变ΔP 和Δε分别为载荷和应变的增量。

由公式（1-2）即可算出弹性模量 E 。

实验方法如图1-1所示，采用矩形截面的拉伸试件，在试件上沿轴向和垂直于轴向的两面各贴两片电阻应变计，可以用半桥或全桥方式进行实验。

1、半桥接法：把试件两面各粘贴的沿轴向（或垂直于轴向）的两片电阻应变计（简称工作片）的两端分别接在应变仪的A、B 接线端上，温度补偿片接到应变仪的B、C 接线端上，然后给试件缓慢加载，通过电阻应变仪即可测出对应载荷下的轴向应变轴r ε值（或横向应变值横r ε）。

再将实际测得的值代入（1-2）式中，即可求得弹性模量 E 之值。

2、全桥接法：把两片轴向（或两片垂直于轴向）的工作片和两片温度补偿片按图1-1中（a)( 或（b)) 的接法接入应变仪的 A 、 B 、 C 、 D 接线柱中，然后给试件缓慢加载，通过电 阻应变仪即可测出对应载荷下的轴向应变值轴r ε（或垂直于轴向横r ε），将所测得的ε值代入（1-2）式中，即可求得弹性模量 E 之值。

(1)§4电测法测定材料的弹性模量E 和泊松比实验1、概述弹性模量E （也称杨氏模量）是表征材料力学性能中弹性段的重要指标之一，它反映了材 料抵抗弹性变形的能力。

泊松比反映了材料在弹性范围内，由纵向变形引起的横向变形的大小。

在对构件进行刚度稳定和振动计算、研究构件的应力和变形时，要经常用到E 和这两个弹性常 数。

而弹性模量E 和泊松比只能通过实验来测定。

2、实验目的验证胡克定律；了解电阻应变片的工作原理及贴片方式; 了解应变测试的接线方式。

3、实验原理 弹性模量E 和泊松比是反映材料弹性阶段力学性能的两个重要指标，在弹性阶段，给一个确定截而形状的试件施加轴向拉力，在截面上便产生了轴向拉应力，试件轴向伸 长，单位长度的 伸长量称之为应变，同样，当施加轴向压力时，试件轴向缩短。

在弹性阶 段，拉伸时的应力与应 变的比值等于压缩时的应力与应变的比值，且为一定值，称之为弹性模量E ，L/L在试件轴向拉伸仲长的同时，其横向会缩短，同样，在试件受压轴向缩短的同时，其横向会伸长，在弹性阶段，确定材质的试件拉仲时的横向应变与试件的纵向应变的比值等于 压缩时横向 应变与试件的 纵向应变的比值，且同样为一定值，称之为泊 松比，横纵L 横/ L0 压力的测量原理同拉、压实验，应变的测量采用电阻应变片电测法原理。

电阻应变片可形彖地理解为按一定规律排列有一定长度的电阻丝，实验前通过胶粘的 方式 将电阻应变片粘贴在试件的表而，试件受力变形时，电阻应变片中的电阻丝的长度也随 之发生相 应的变化，应变片的阻值也就发生了变化。

实验中我们采用的应变片是由两个单向应变片组成的 十字形应变花，所谓单向应变片，就是应变片的电阻值对沿某一个方向的变形最为敏感，称此 方向为应变片的纵向，而对垂直于该方向的变形阻值变化可忽略，称此方向为应变片的横向。

利用应变片的这个特性，在进行应变测试时，我们所测到只是试件沿应变 片纵向的应变，其不 包含试件垂直方向变形所引起的影响。

弹性模量e和泊松比的测定实验总结实验总结：
弹性模量e和泊松比的测定实验旨在利用杨氏模量对弹性模量e和泊松比的测定，也可以在不影响材料性质的条件下测量材料的抗变形特性。

实验前准备：
1.实验需要用到具有良好精度的硬度计，放大器和痕实验夹具，以确保实验精确度。

2.用于测试的材料必须完整无缺，确保其强度，以保障实验结果的正确性。

实验步骤：
步骤一：将硬度计放入夹具中，并调节放大器，以确保数据的精确性。

步骤二：加载恒定负荷到材料的径向部分，使其受到痕压，并记录因痕应力和应变而产生的结果。

步骤三：将记录下来的数据用图形标明，以便在其中计算e 和泊松比m。

步骤四：根据计算结果计算弹性模量e和泊松比m，并用该结果来描述材料的抗变形特性。

实验结论：
通过弹性模量e和泊松比m的测定实验，我们可以获得被测材料的抗变形性能，从而进一步估算材料的运行参数，实现对该种材料的更有效的应用。

这也表明了在实际工程中，要将弹性模量e和泊松比m用来工程设计中学习材料运行机理，预测材料的变形以及力学行为，增强设计效益。

材料弹性模量及泊松⽐测试实验教案.材料弹性模量及泊松⽐测试实验教学内容：⼀、电测法原理 1、应变⽚测试原理 2、惠斯登路桥应⽤（1）1/4桥温度补偿⽚(R 2) （2）半桥（3）全桥⼆、应变⽚的粘贴步骤 1、选⽚2、测点表⾯的清洁处理3、贴⽚4、⼲燥处理5、接线6、防潮处理三、材料弹性模量和泊松⽐的测定包括实验⽬的、实验内容、实验（设计）仪器设备和材料清单、实验原理、实验步骤及结果测试等。

四、应变仪的操作⽅法教学要求：理解电测法的原理、应变⽚的粘贴步骤；掌握材料弹性模量和泊松⽐测定的原理及应变仪的使⽤。

重点：电测法原理，实验原理，应变仪的使⽤。

⼀、电测法原理1、应变⽚测试原理电测法是⼯程上常⽤的对实际构件进⾏应⼒分析实验的⽅法之⼀。

它是通过贴在构件被测点处的电阻应变⽚(以下简称应变⽚)，将被测点的应变值转换为应变⽚的电阻变化，再利⽤电阻应变仪测出应变⽚的电阻变量，并直接转换输出应变值，然后依据虎克定律计算出构件被测点的应⼒值的⼤⼩。

在电测法中，主要设备是电阻应变⽚和电阻应变仪。

其中，电阻应变⽚是将应变变化量转变成电阻变化量的转换组件。

应变电测发具有感受元件重量轻，体积⼩；量测系统信号传递迅速、灵敏度⾼、可遥感，便于与计算机连⽤及实现⾃动化等优点。

它的⼯作原理很简单，是依据⾦属丝的电阻R 与其本⾝长度L 成正⽐，与其横截⾯积A 成反⽐这⼀物理学定律⽽得，⽤公式表⽰其电阻即为：/(R L A ID ρ=为电阻系数）当电阻丝受到轴向拉伸或压缩时，上式中的L 、A 、p 均将发⽣变化。

若此时对上式两端同取对数，即有：ln ln ln ln R L A ρ=+-对其进⾏数学求导，有：////dR R d dL L dA A ρρ=+-因为⾦属电阻线受轴向拉伸(或压缩)作⽤时，式中：所以上式可写成：并令式中：u--电阻丝材料的泊松⽐K。

—单丝灵敏系数。

则：对⼤多数电阻丝⽽⾔，K0为常量，对丝栅状应变⽚或箔式应变⽚，考虑到已不是单根丝，故改⽤灵敏系数K代替代。

材料弹性模量及泊松比的测定实验报告材料弹性模量及泊松比的测定实验报告引言：弹性模量和泊松比是材料力学性质的重要参数，对于材料的设计和工程应用具有重要意义。

本实验旨在通过测定材料的弹性模量和泊松比，了解材料的力学性能，为工程应用提供参考。

实验原理：弹性模量是材料在受力时对应变的抵抗能力，是表征材料刚度的指标。

泊松比则是材料在受力时横向收缩与纵向伸长之间的比值，是表征材料变形性能的参数。

实验步骤：1. 实验材料准备：选取一种材料样本，如金属棒或弹簧。

2. 弹性模量测定：将材料样本固定在实验台上，用一定的力对其施加拉伸或压缩力，测量应变和应力的关系，通过斜率计算弹性模量。

3. 泊松比测定：将材料样本固定在实验台上，施加纵向力，测量纵向应变，再施加横向力，测量横向应变，通过应变比值计算泊松比。

实验结果：根据实验数据计算得出材料的弹性模量和泊松比。

实验结果显示，材料的弹性模量为X GPa，泊松比为X。

讨论与分析：根据实验结果，我们可以对材料的力学性能进行分析和讨论。

弹性模量越大，材料的刚度越高，对外力的抵抗能力越强。

而泊松比则反映了材料在受力时的变形性能，泊松比越小，材料的变形能力越差，对外力的响应越迟缓。

实验误差及改进：在实验过程中，可能会存在一定的误差。

例如，由于材料的制备和实验条件的限制，实际测量值与理论值之间可能存在一定的偏差。

为了减小误差，可以增加样本数量，进行多次测量取平均值，或者改进实验装置，提高测量精度。

实验应用：弹性模量和泊松比是材料工程中常用的参数，对于材料的设计和工程应用具有重要意义。

例如，在建筑工程中，需要选取合适的材料来承受外力，弹性模量和泊松比的测定可以帮助工程师选择合适的材料。

此外，在材料科学研究中，弹性模量和泊松比的测定也是评价材料性能的重要手段。

结论：通过本实验的测定，我们成功地得到了材料的弹性模量和泊松比。

这些参数对于材料的力学性能研究和工程应用具有重要意义。

实验结果与理论值存在一定的偏差，但通过改进实验方法和提高测量精度，可以进一步提高实验结果的准确性。