下载文档原格式
极化恒等式【一.式子结构分析】 1.()2222a ba ab b +=++r r r r r r ，同理可以有：()2222a ba ab b -=-+r r r r r r .两个式子相加可得：()()()22222a b a ba b +=++-r rr r r r ,这个说明平行四边形对角线的平方和等于四边的平方和，也等于邻边的平方和的两倍，由此可得三角形的中线长公式：a m =本20页）. 2.()2222a ba ab b +=++r r r r r r ，同理可以有：()2222a ba ab b -=-+r r r r r r .两个式子相减可得：()()224a ba b a b +--⋅=r r r r rr ,这个叫极化恒等式，2017年全国甲卷理科选择最后一题考查了.3. 很多时候我们也会遇到22a b -r r 这样的式子，一般22()()a b a b a b -+=-r r r r r r ，类似于平方差公式，实质上同2差不多【二、极化恒等式】和数学上很多经典的公式定理一样，极化恒等式也并没有那么神秘，甚至说是很基本. 回忆必修四105页例2()2222a ba ab b +=++r r r r r r ，同理可以有：()2222a ba ab b -=-+r r r r r r .两个式子相加可得：()()()22222a b a ba b +=++-r rr r r r ,这个说明平行四边形对角线的平方和等于四边的平方和，也等于邻边的平方和的两倍，由此可得三角形的中线长公式：a m =本20页）.两个式子相减可得：()()224a ba b a b +--⋅=r r r r rr ,这个叫极化恒等式，2017年全国甲卷理科选择最后一题考查了.极化恒等式的几何意义是:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14，即221()4a b AD BC ⋅=-r r .在三角形中，也可以用三角形的中线来表示，即2214a b AM BC ⋅=-r r ，他揭示了三角形的中线与边长的关系.下面通过几道题目，来分析极化恒等式的妙用.4. 在ABC ∆中，M 是BC 的中点，3,10AM BC ==，则AB AC ⋅=u u u r u u u r________.解析： ()22()4AB ACAB AC AB AC +-⋅=-u u u r u u u r u u u r u u u r u u u r u u u r224BC AM -=u u u ru u u u r 16=- 事实上，类似的问题时有看到，只是很多时候用其他的方法取代了“极化恒等式”，或在无意中使用“极化恒等式”.在ABC ∆中，D 是BC 的中点，2,3AB AC ==，则AD BC ⋅=u u u r u u u r________.解析： ()()2AB ACAD BC AB AC +⋅=⋅-u u u r u u u r u u u r u u u ru u u r u u u r 221()2ABAC =-u u ur u u u r 52=.5. 在Rt △ABC 中，CA ＝CB ＝3，M ，N 是斜边AB上的两个动点，且MN =CM CN u u u u r u u u rg的取值范围为_______.解析：设MN 的中点为D ，则()()2214CM CN CM CN CM CN ⎡⎤=+--⎢⎥⎣⎦u u u u r u u u r u u u u r u u u ru u u u r u u u r g()[]22241124,26CD MN CD ⎡⎤=-=-⎢⎥⎣⎦∈u u u r u u u u r u u u r 类题：△ABC 中，AC ⊥BC ，AB ＝3，AC ＝1，D 为BC 的中点，F 为线段AD 上任意一点，求()AF FB FC+u u u r u u u r u u u rg 的最大值.解析：()22AF FB FC AF FD AF FD +==u u u r u u u r u u u r u u u r u u u rg gg ，因AF FD AD +==，故当AF FD ==()AF FB FC +u u u r u u u r u u u r g 取最大值32.6. （2017年高考全国卷Ⅱ理12）已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+u u u r u u u r u u u r的最小值是A.2-B.32-C. 43- D.1- 解法分析思路一：建系，将向量运算坐标化解法1：如图1，建立平面直角坐标系xOy，(A ，()1,0B -，()1,0C ，设(),P x y ，则()PA x y =-u u u r，()()()1,1,2,2PB PC x y x y x y +=---+--=--u u u r u u u r ，所以()(2223322222PA PB PC x y y x y ⎡⎤⎛⎢⎥+=+-=+-- ⎢⎥⎝⎭⎦≥⎣u u u r u u u r u u u r g ， 当且仅当0x =，2y =，即P 为AO 的中点时取等号，则所求最小值为32-，选B.图1思路二：取BC 中点M ，将PB PC +u u u r u u u r 转化为2PM u u u u r ，则()22PA PB PC PA PM PA PM +==u u u r u u u r u u u r u u u r u u u u r u u u r u u u u rg g g ，怎么求PA PM u u u r u u u u rg 的最小值呢？如图2，设AM 的中点为N ，则()()()()22222113324444PA PM PA PM PA PM PN MA PN ⎡⎤⎡⎤=+--=-=--⎢⎥⎢⎥⎣⎦⎣≥⎦u u u r u u u u r u u u r u u u u r u u u r u u u u r u u u r u u u r u u u r g ，当且仅当20PN =u u u r ，即P 与N 重合（P 为AM 的中点）时取等号，故PA PM u u u r u u u u r g 的最小值为34-，所求最小值为33242⎛⎫⨯-=- ⎪⎝⎭，选B. 注：（1）转化PA PM u u u r u u u u r g 时用到了极化恒等式()()2214PA PM PA PM PA PM⎡⎤=+--⎢⎥⎣⎦u u u r u u u u r u u u r u u u u r u u u r u u u u r g ，其一般形式为()()2214a b a b a b ⎡⎤=+--⎢⎥⎣⎦r r r r r r g ；（2）PA PM u u u r u u u u r g 也可这样转化： PA PM =u u u r u u u u r g ()()PN NA PN NM ++u u u r u u u r u u u r u u u u r g ()()PN NA PN NA =+-u u u r u u u r u u u r u u u r g 22234PN NA PN =-=-u u u r u u u r u u u r .图2类题：已知动点M 是腰长为2的等腰直角三角形ABC ∆（C ∠为直角）的三边上的动点，则(+)MA MB MC ⋅u u u r u u u r u u u u r的取值范围是（ ）A ．1[,0]2- B ．[0,4] C ．1[,4]2-D．答案：C解析：取AB 中点D ，CD 中点E ，则(+)MA MB MC ⋅u u u r u u u r u u u u r2MD MC =⋅u u u u r u u u u r()()22124MD MCMD MC ⎡⎤=⨯+--⎢⎥⎣⎦u u u ur u u u u r u u u u r u u u u r 22214212ME CD ME ⎡⎤=-=-⎢⎥⎣⎦u u u r u u u r u u u r7. ***如图，在凸四边形ABCD 中，66AB AD BD ⋅==u u u r u u u r ，，O 是BD 的中点，且3AO OC =u u u r u u u r，则CB CD ⋅u u u r u u u r等于（ ）A ．115- B ．89-C ．223-D ．83解析：22(+)()4AB AD AB AD AB AD --⋅=u u u r u u u r u u u r u u u r u u u r u u u r 222494AO DB AO -==-u u u r u u u ru u u r 6=22(+)()4CB CD CB CD CB CD --⋅=u u u r u u u r u u u r u u u ru u u r u u u r 29CO =-u u u r 223=-.8. ***（2013年浙江高考理）ABC ∆中0P 是边AB 上一定点，满足014P B AB =，且对于边AB 上任取的一点P ，恒有00PB PC P B PC ⋅≥⋅u u u r u u u r u u u r u u u r，则( )A ．B ．C ．D ．【答案】D解析： 法1：【将式子转化为与某一个变量有关系的式子，即函数式.由已知条件，当14PB AB =时，函数式子取最大值】设,PB x BC a ==，作CH AB ⊥，则cos BH a B =.则22()cos PB PC PB PB BC PB BP BC x xa B ⋅=⋅+=-⋅=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r由题意，当且仅当111cos 224x a B BH AB ===时，上式 有最小值.此时，H 也为AB 的中点，故AC BC =.法2：由题意，设|→AB |=4，则|→P 0B |=1，过点C 作AB 的垂线，垂足为H ，在AB 上任取一点P ，设HP 0=a ，则由数量积的几何意义可得，→PB ∙→PC =|→PH ||→PB |=(|→PB | −(a +1))|→PB |，→P 0B ∙→P 0C =−|→P 0H ||→P 0B |=−a ，于是→PB ∙→PC ≥→P 0B ∙→P 0C 恒成立，相当于(|→PB |−(a +1))|→PB |≥−a 恒成立，整理得|→PB |2−(a +1)|→PB |+a ≥0恒成立，只需∆=(a +1)2−4a =(a −1)2≤0即可，于是a =1，因此我们得到HB =2，即H 是AB 的中点，故△ABC 是等腰三角形，所以AC =BC法3：如图建系，设(,0),(,),(,0)C C B b C x y P x ， 2()CCPB PC x b x x bx ⋅=-++u u u r u u u r ，当且仅当24C b x b x +==时，上式取最小值，此时2C bx =，故AC BC =. 法4：以AB 中点为坐标原点建系也可，同法2.法5: 极化恒等式 224=()()a b a b a b ⋅+--r r r r r r如图，取线段BC 的中点M ，则22224=()()4PB PC PB PC PB PC PM BC ⋅+--=-u u u r u u u r u u u r u u u r u u u r u u u r ， 要使得4PB PC ⋅u u u r u u u r 的值最小，只需24PM u u u u r 取最小值.因为P 是线段AB 上动点，所以只有当PM AB⊥时，PM u u u u r取得最小值，且点P 与点0P 必须重合，M 是线段BC 的中点，只有AC=BC 时才能成立.090=∠ABC 090=∠BAC AC AB =BC AC =CBAHC BAxPy9. ***（2012年安徽卷）若平面向量,a b r r 满足23a b -r r≤，则a b ⋅r r 的最小值是_________.解析：2212(2)(2)4a b a b a b ⎡⎤⋅=+--⎣⎦r r r r r r 219(2)44a b ---r r ≥≥.所以98a b ⋅-r r ≥.A.32+ B. 12+ C. 322+ D. 122+解：法1：全部与圆心联系起来，基本定义设AB 中点为D ，=()()PA PB PO OA PO OB ⋅+⋅+u u u r u u u r u u u r u u u r u u u r u uu r22PO PO OD OA OB =+⋅+⋅u u u r u u u r u u u r u u u r u u u r1122PO OD =+⋅+u u u r u u ur 3,2PO OD =<>u u u r u u u r，∵cos ,[1,1]PO OD <>∈-u u u r u u u r ，∴PA PB ⋅u u u r u u u r的范围为33[22.法2：建立坐标系，需要用到辅助角公式以O 点为原点，OA 为x 轴建立平面直角坐标系，则1(1,0),(,)22A B ， （也可设点11),)22A B -） 设(cos ,sin ),02P αααπ≤<，则1(1cos ,sin ),(cos sin ),2PA PB αααα=--=--u u u r u u u r 1(1cos )(cos )(sin sin )2PA PB αααα⋅=--+--u u u ru u u r33cos 222αα=--313(sin )222αα=+3)23πα=+∵1sin()13πα-≤+≤，∴333)2232πα≤+≤，故PA PB ⋅u u u r u u u r 的范围为33[3,3]22-+.法3：建立坐标系，设点3131(,),(,)22A B -，(,)P x y ， 332PA PB x ⋅=-u u u r u u u r法4：转化为求三角形的面积的最大值，使用余弦定理和基本不等式cos cos30PA PB PA PB APB PA PB ⋅=⋅∠=⋅u u u r u u u r u u u r u u u r u u u r u u u r 32PA PB =⋅u u u r u u u r ， 根据余弦定理和基本不等式2220cos302PA PB AB PA PB +-⋅=u u u r u u u r 12PA PB ⋅-≥， 法5：转化为求三角形的面积的最大值，使用余弦定理和基本不等式求32PA PB ⋅u u ur u u u r 的最大值也即求三角形的面积的最大值，也即求点 P 到AB 距离的最大值 法6：与三角形中点联系起来设AB 中点为D ， 则=()()PA PB PD DA PD DB ⋅+⋅+u u u r u u u r u u u r u u u r u u u r u u u r =()()PD DA PD DA +⋅-u u u r u u u r u u u r u u u r22214PD DA PD =-=-u u u r u u u r u u u r易知，PD u u u r 的范围是33[1,1]-+，故PA PB ⋅u u u r u u u r 的范围为33[3,3]22-+.11. ***（2011年浙江卷）已知直线AB 与抛物线24y x =交于点,A B ，点M 为AB 的中点，C 为抛物线上一个动点，若0C 满足{}00min C A C B CA CB ⋅=⋅u u u u r u u u u r u u r u u u r，则下列一定成立的是（ ）A.0C M AB ⊥B.0C M l ⊥u u u u u r，其中l 是抛物线过0C 的切线C.00C A C B ⊥D.0C M AB = 答案 D解析 如图所示，极化恒等式 CA →·CB →＝(AM →－CM →)·(BM →－CM →)＝CM →2－(BM →＋AM →)·CM →＋AM →·BM →＝CM →2－14AB →2，当直线AB 一定时，当且仅当|CM →|取得最小值时，使得CA →·CB →取最小值， 只有当C M ⊥l 时，|CM →|取得最小值，故选D.【注】本题实质上就是求抛物线上一点到其内一点距离的最小值下面用两种方法来证明，法1：几何分析法，只需证明CM 不与l 垂直时，有比CM 还要短的. 这一招太聪明了，如果直接证明CM 最短很不好证. 设过点C '的切线为l ',此时C M '不与l '垂直，作MH l '⊥， 交抛物线于点1C .则1MC MH MC MC '>>>. 法2：求导运算22200()()CM x x y y =-+-2222000022x x x x y y y y =-++-+22222200002222y y x x y y y y ⎛⎫=-++-+ ⎪⎝⎭22222200002222y y x x y y y y ⎛⎫=-++-+ ⎪⎝⎭()f y =300()2(1)20f y y x y y '=+--=时，上式有最小值？？？？【注】此处如何整理出 CM ⊥CA 时，0011y y x x y-⋅=--，整理得3002(1)20y x y y +--=，两条件相同. 12. 已知圆O 的半径为2，,P Q 是圆O 上任意两点，且060POQ ∠=，AB 是圆O 的一条直径，若点C满足(1)OC OP OQ λλ=-+u u u r u u u r u u u r，则CA CB ⋅u u r u u u r 的最小值是（ ） A ．1- B ．2- C ．3- D ．4-解析：由(1)OC OP OQ λλ=-+u u u r u u u r u u u r 得，点C 在PQ 上，24CA CB CO ⋅=-u u r u u u r易得当且仅当C 为PQ 中点时，CO 有最小值1-.变式：已知圆O 的半径为2，,P Q 是圆O 上任意两点，且060POQ ∠=，AB 是圆O 的一条直径，若点C 满足(1)OC OP OQ λλ=-+u u u r u u u r u u u r，则CA CB ⋅u u r u u u r 的最小值是（ ）A ．1-B ．2-C ．3-D ．4-解析：设OP OP '=-u u u r u u u r ，所以(1)(1)OC OP OQ OP OQ λλλλ'=-+=-+u u u r u u u r u u u r u u u r u u u r， 点C 在P Q '上，24CA CB CO ⋅=-u u r u u u r易得当且仅当C 为PQ 中点时，CO 有最小值3-. 【三. 三角形向量中线公式和中点转化】13. ***点O 是ABC ∆的三边中垂线的交点，a ，b ，c 是角A ，B ，C 的对边，已知2220,13b b c b -+=<<，则BC AO u u u r u u u rg 的范围是____________．解析：O 是ABC ∆的外心，设BC 中点为M ，则OM BC ⊥()BC AO BC AM MO BC AM u u u r u u u r u u u r u u u u r u u u u r u u u r u u u u r g g g =+=2211()()()22AC AB AC AB b c u u u r u u u r u u u r u u u r g =-+=-2b b =-.因为2220b b c -+=，所以2220c b b =->，所以02b <<，又13b <<，所以12b <<.所以BC AO u u u r u u u rg 的范围是（0，2）.14. 已知圆22:1C x y +=，点00(,)P x y 是直线:3240l x y +-=上的动点，若在圆C 上总存在两个不同的点,A B ，使OA OB OP +=u u u r u u u r u u u r，则0x 的取值范围是（ ）A ．24(0,)13B ．24(,0)13- C ．13(0,)24 D ．13(0,)12 答案：A【解析】法1：如图，∵OA OB OP +=u u u r u u u r u u u r；∴OP 与AB 互相垂直平分，∴圆心到直线AB 的距离122020<+y x ；∴42020<+y x ①； 又042300=-+y x ；∴00232x y -=， 代入①得：4232202<⎪⎭⎫ ⎝⎛-+x x ；解得132400<<x ；∴0x 的取值范围是24(0,)13．故选：A ．法2：OP=2时，是临界状态，求出即可.15. ***在ABC ∆中，D 是BC 边上任意一点（D 与B ，C 不重合），且22+AB AD BD DC =⋅，则ABC∆一定是（ ）A ．直角三角形B ．锐角三角形C ．等腰三角形D ．等边三角形解析：类似于平方差公式，22AB AD -表示成向量的平方22AB AD -u u u r u u u r ，可以转化运算 22+AB AD BD DC =⋅u u u r u u u r u u u r u u u r ,220AB AD BD DC --⋅=u u u r u u u r u u u r u u u r ,()0DB AB AC ⋅+=u u u r u u u r u u u r，故是等腰，选C.16. （1）已知圆直径=6AB ，O 点为圆心，C 为半径上不同于A 、B 的任意一点，若P 为半径OC 上的动点，(+)PA PB PC ⋅u u u r u u u r u u u r的最小值是_________.解：(+)2PA PB PC PO PC ⋅=⋅u u u r u u u r u u u r u u u r u u u r 262PO PO =-+92-≥.（2）已知圆半径为1，圆上的弦AB 长为1，P 为圆上的动点，PA PB ⋅u u u r u u u r的最大值是（ ）A.332+ B. 132+ C. 332+ D. 132+ 解： 设AB 中点为D ， 则=()()PA PB PD DA PD DB ⋅+⋅+u u u r u u u r u u u r u u u r u u u r u u u r =()()PD DA PD DA +⋅-u u u r u u u r u u u r u u u r22214PD DA PD =-=-u u u r u u u r u u u r易知，PD u u u r 的范围是33[1,1]-+，故PA PB ⋅u u u r u u u r 的范围为33[3,3]22-+. 17. （1）已知直角梯形ABCD ，AD ∥BC ，090BAD ∠=，AD=2，BC=1，P 是腰AB 上的动点，则+PC PD u u u r u u u r的最小值为_____. 法1：建系，设(0,)P b法2：取CD 中点Q ，+2PC PD PQ =u u u r u u u r，易得P 是AB 的中点时取最小.（2）已知点A ，B ，C 在圆221x y +=上运动，且AB BC ⊥，若点P 的坐标为(2,0)，则PA PB PC ++u u u r u u u r u u u r的最大值为（ ）A.6B.7C.8D.9 【答案】B.法2：因AB BC ⊥，所以AC 为直径，O 为AC 中点，2PA PB PC PO PB ++=+u u u r u u u r u u u r u u u r u u u r，当(1,0)B -时，最大，为7.18. ***如图，在梯形ABCD 中，CD AB //，2=AB ，4=CD ，5==AD BC ，E ，F 分别是AD ，BC 的中点，对于常数λ，在梯形ABCD 的四条边上恰有8个不同的点P ，使得λ=⋅PF PE 成立，则实数λ的取值范围是（ ）A ．)209,45(-- B ．)411,45(- C ．)411,41(- D ．)41,209(-- 答案：D【解析】法1：以CD 中点为坐标原点，CD 所在直线为x 轴建立直角坐标系， 则33(1,2),(1,2),(2,0),(2,0),(,1),F(,1)22A B C D E ---，当P 在CD 边上时，设(,0),||(0,2)P x x ∈，则25511(,)444PE PF x λ=⋅=-∈-u u u r u u u r，对应值都有两个；当P 在AB 边上时，设(,2),||(0,1)P x x ∈，则2551(,)444PE PF x λ=⋅=-∈--u u u r u u u r ，对应值都有两个；当P 在BC 边上时，设(,42),(1,2)P x x x -∈，则2275124PE PF x x λ=⋅=-+u u u r u u u r ，当91(,)204λ∈--时，每一个λ都有两个x 与之对应； 根据对称性，当P 在AD 边上时，同P 在BC 边上时.综上，若有8个不同的点P ，使得λ=⋅PF PE 成立，则实数λ的取值范围是9151191(,)(,)(,)20444204---=--I ，选D. 法2：（巧取中点转化，极化恒等式）取EF 中点H ，取AB 中点M ，取CD 中点N ，1MH NH == 则()()PE PF PH HE PH HF ⋅=+⋅+u u u r u u u r u u u r u u u r u u u r u u u r 2212PH HE =-u u u r u u u r 2214PH EF =-u u u r u u u r 29=4PH -u u u r ，当P 在AB 边上时，2951=(,)444PE PF PH λ=⋅-∈--u u u r u u u r u u u r ，根据对称性，对应值都有两个；当P 在CD 边上时，29511(,)444PH λ=-∈-u u u r ，根据对称性，对应值都有两个；当P 在AD 边上时，PH 的最小值即H 到AD 的距离，由等积法min 5PH =，又2AH =，当(,2)5PH ∈时，91(,)204λ∈--，对应值都有两个；根据对称性，当P 在AD 边上时，同P 在BC 边上时. 综上，若有8个不同的点P ，使得λ=⋅PF PE 成立，则实数λ的取值范围是9151191(,)(,)(,)20444204---=--I ，选D. 19. 如图，在同一平面内，点P 位于两平行直线l 1，l 2同侧，且P 到l 1，l 2的距离分别为1,3.点M ，N 分别在l 1，l 2上，|PM →＋PN →|＝8，则PM →·PN →的最大值为( ) A ．15 B ．12 C ．10 D ．9 答案 A解析：取MN 中点O ，则()142PO PM PN =+=u u u r u u u ur u u u r ，1OM u u u u r ≥ ()()PM PN PO OM PO ON =++u u u u r u u u r u u u r u u u u r u u u r u u u rg g 22216PO OM OM =-=-u u u r u u u u r u u u u r 22216PO OM OM =-=-u u u r u u u u r u u u u r20. ***已知ABC ∆的面积为2，E,F 是AB ，AC 的中点，P 为直线EF 上任意一点，则2PB PC BC ⋅+u u u r u u u r u u u r 的最小值为（ ）A ．2B ．3C ．23D ．4 解析：法1：巧取中点转化法，极化恒等式取BC 中点D ，设底边BC 的高为h ，则12PD h ≥，22()()PB PC BC PD DB PD DC BC +=+++u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r g g222PD DB BC =-+u u u r u u u r u u u r 2234PD BC =+u u u r u u u r 2222313444PD BC h BC =++u u u r u u u r u u u r ≥==≥ 法2：建立平面直角坐标系(如图所示)，【四、极化恒等式在立体几何中的应用】21. 正方体1111ABCD A B C D -的棱长为2，MN 是它内切球的一条弦（把球面上任意2点之间的线段称为球的弦），P 为正方体表面上的动点，当弦MN 最长时，PM PN ⋅u u u u r u u u r 的最大值为_________.解析：设球心为O ，易得球的半径1R =，2221=(2)14PM PN PO R PO ⋅-=-u u u u r u u u r u u u r u u u r ，易得PO PM PN ⋅u u u u r u u u r 的最大值为2.22. 点P 是棱长为1的正方体1111ABCD A B C D -的底面1111A B C D 上一点，则PA PC ⋅u u u r u u u r 的取值范围是_________.解析：设AC 的中点为M ，224PA PC PM AC ⋅=-u u u r u u u r u u u u r u u u r 242PM =-u u u u r 1,12⎡⎤∈⎢⎥⎣⎦23.24.。
极化恒等式这个概念虽在课本上没有涉及，但在处理一类向量数量积时有奇效，备受师生喜爱.1. 极化恒等式： 221()()4a b a b a b ⎡⎤⋅=+--⎣⎦ 2. 极化恒等式三角形模型：在中，D 为BC 的中点，则ABC ∆221||||4AB AC AD BC ⋅=- 3. 极化恒等式平行四边形模型：在平行四边形ABCD 中，221(||||)4AB AD AD BD ⋅=-类型一 利用极化恒等式求值典例1.如图在三角形ABC 中，D 是BC 的中点，E,F 是AD 上的两个三等分点，则4,1,BA CA BF CF ⋅=⋅=-值为______.BE CE ⋅【答案】78【解析】设2222,,||||94DC a DF b BA CA AD BD b a ==⋅=-=-= 2222||||1BF CF FD BD b a ⋅=-=-=- 解得22513,88b a == 22227||||48BE CE ED BD b a ∴⋅=-=-=高三数学复习微专题之平面向量篇第二讲：极化恒等式问题类型二 利用极化恒等式求最值或范围典例2 在三角形ABC 中，D 为AB 中点，，E,F 分别为BC,AC 上的动点，且90,4,3C AC BC ︒∠===EF=1，则最小值为______DE DF ⋅【答案】154【解析】设EF 的中点为M ，连接CM ，则 1||2CM =即点M 在如图所示的圆弧上，则222211115||||||||4244DE DF DM EM DM CD ⋅=-=---= ≧类型三 利用极化恒等式求参数典例3 设三角形ABC ，P 0是边AB 上的一定点，满足P 0B=AB,且对于边AB 上任一点P ，恒有14,则三角形ABC 形状为_______.00PB PC P B P C ⋅≥⋅【答案】C 为顶角的等腰三角形. 【解析】取BC 的中点D ，连接PD,P 0D.00PB PC P B P C ⋅⋅ …2222011||||||44PD BC P b BC ∴-- …,设O 为BC 的中点，0||PD P D ∴…0P D AB ∴⊥OC AB AC BC ∴⊥∴=即三角形ABC 为以C 为顶角的等腰三角形.模拟：1.已知是边长为2的等边三角形，P 为平面ABC 内一点，则的最小值是_____ABC ∆()PA PB PC ⋅+【答案】 32-【解析】设BC 的中点为O ，OC 的中点为M,连接OP,PM,当且仅当M 与P 重合时取等号222133()22||||2||222PA PB PC PO PA PM AO PM ∴⋅+=⋅=-=-≥-2．直线与圆相交于两点M,N,若，P 为圆O 上任意一点，则0ax by c ++=220:16x y +=222c a b =+的取值范围为_______PM PN ⋅【答案】【解析】[6,10]-圆心O 到直线的距离为0ax by c ++=1d ==设MN 的中点为A ，222||||||15PM PN PA MA PA ⋅=-=-||||||||||OP OA PA OP OA -+ (2)3||5,||15[6,10]PA PM PN PA ∴⋅=-∈- ……3．如图，已知B,D 是直角C 两边上的动点，12,||,()6AD BD AD BAD CM CA CB π⊥=∠==+，则的最大值为______1()2CN CD CA =+CM CN ⋅【答案】【解析】14)4+设MN 的中点为G ，BD 的中点为H ，21||4CM CN CG ⋅=- 221||||16MN CG =-21111||||||4)22164CG CH HG CM CN ⎛+=+⋅+-= ⎝……所以的最大值为CM CN ⋅14)4+4.如图在同一平面内，点A 位于两平行直线m,n 的同侧，且A 到m,n 的距离分别为1，3，点B,C 分别在m,n上，且，则的最大值为______||5AB AC +=AB AC ⋅【答案】【解析】连接BC ，取BC 的中点D ，则，21422AB AC AD BD ⋅=- 又故15||22AD AB AC =+= 2225251444AB AC BD BC ⋅=-=- 又因为所以min312BC =-=21()4max AB AC ⋅= 5.在半径为1的扇形AOB 中，,C 为弧上的动点，AB 与OC 交于点P ，则的最小值为60AOB ︒∠=OP BP ⋅_____【答案】 41-【解析】取OB 的中点D ，连接PD ，则于是只要求求PD 的最小值即可，22214OP BP PD OD PD ⋅=-=-由图可知，当时，即所求最小值为 PD AB ⊥ min PD =41-6.已知线段AB 的长为2，动点C 满足（为常数），且点C 总不在以点B 为圆心，为半径的CA CB λ⋅= λ12圆内，则负数的最大值为______ λ【答案】 43-【解析】如图取AB 的中点为D ，连接CD,则21CA CB CD λ⋅=-=又由点C 总不在以点B 为圆心，为半径的圆内，，则负数的最大10CD λ=-< (1212)λ值为43-7.已知A(0,1)，曲线横过点B ，若P 是曲线C 上的动点，且的最小值为2，则4:log C y x =AB AP ⋅α=______ 【答案】 e 【解析】如图，B （1，0），则，连接BP ，取BP 的中点C ，连接AC,AB =因为的最小值为2，则有上式等价于，AB AP ⋅ ()2222max2AC BCAB -===222AB BC AC +…即当且仅当P 与B 重合时取等号，此时曲线C 在B 处的切线斜率等于1，90ABP ︒∠…即11n ,e l a α==8.若平面向量满足，则的最小值为_____,a b |2|3a b -≤a b ⋅ 【答案】98-【解析】222222(2)(2)|2||2|0398888a b a b a b a b a b +--+---⋅==≥=-当且仅当，即时取最小值|2|0,|2|3a b a b +=-=33||,||,,42a b a b π==<>= a b ⋅ 98-9.在正方形ABCD 中，AB=1，A,D 分别在x,y 轴的非负半轴上滑动，则的最大值为_____OC OB ⋅【答案】 2【解析】如图取BC 的中点E ，取AD 的中点F ，所以222224()()(2)(2)41OC OB OC OB OC OB OE BE OE ⋅=+--=-=- 214OC OB OE ⋅=- 而，113|||||||||||1222OE OF FE AD FE ≤+=+=+= 当且仅当时取等号，所以的最大值为2,OF AD OA OD ⊥=OC OB ⋅10.已知正方形ABCD 的边长为2，点E 为AB 的中点，以A 为圆心,AE 为半径作弧交AD 于F ，若P 为劣弧EF上的动点，则的最小值为______PC PD ⋅【答案】5-【解析】如图取CD 的中点M.222224()()(2)(2)44PC PD PC PD PC PD PM DM PM ⋅=+--=-=- 所以21PC PD PM ⋅=-而，当且仅当P,Q 重合时等号成立||1||||||PM PM AP AE +=+≥=所以的最小值为PC PD ⋅21)15--=-11.正方体ABCD-A 1B 1C 1D 1的棱长为2，MN 是它的内切球的一条弦，P 为正方体表面上的动点，当弦MN 的长度最大时，求的范围.PM PN ⋅【答案】 [0,2]【解析】如图当弦MN 的长度最大时，为内切球的直径，此时O 为MN 的中点，所以222224()()(2)(2)44PM PN PM PN PM PN PO OM PO ⋅=+--=-=- 21PM PN PO ⋅=-而，所以的范围为1||PO ≤≤PM PN ⋅ [0,2]。
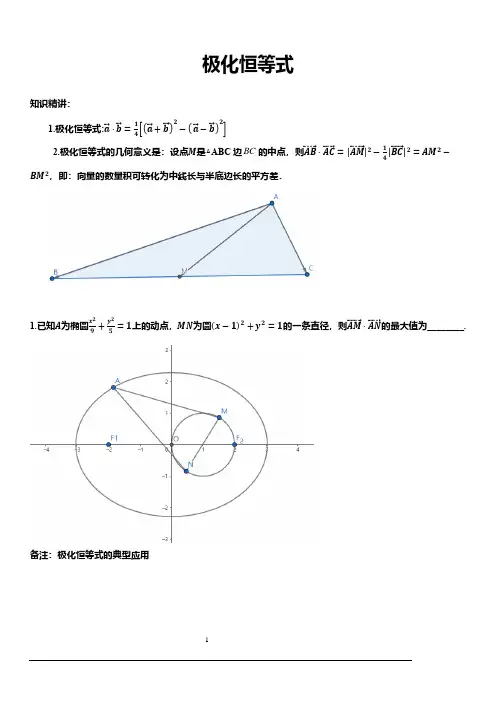
极化恒等式知识精讲：1.极化恒等式:a ⃗ ⋅b ⃗ =14[(a ⃗ +b ⃗ )2−(a ⃗ −b⃗ )2] 2.极化恒等式的几何意义是：设点M 是△ABC 边的中点，则AB⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|AM ⃗⃗⃗⃗⃗⃗⃗ |2−14|BC ⃗⃗⃗⃗⃗⃗ |2=AM 2−BM 2，即：向量的数量积可转化为中线长与半底边长的平方差．1.已知A 为椭圆x 29+y 25=1上的动点，MN 为圆(x −1)2+y 2=1的一条直径，则AM ⃗⃗⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ 的最大值为________.备注：极化恒等式的典型应用BC2. （三星）（2017全国2理）已知ΔABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA ⃗⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )的最小值是（ ）A.−2B.−32 C. −43 D.−1 解：方法一：建系法连接OP ，OA⃗⃗⃗⃗⃗⃗ =(0,√3)，OB ⃗⃗⃗⃗⃗⃗ =(−1,0)，OC ⃗⃗⃗⃗⃗⃗ =(1,0). PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ，∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(−x,−y )⋅(−x,√3−y) ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =x 2+y 2−√3y =x 2+(y −√32)2−34 ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−34，∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32 ∴最小值为−32方法二：均值法∵PC ⃗⃗⃗⃗⃗ +PB⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ，∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ 由上图可知：OA ⃗⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗⃗ −PO ⃗⃗⃗⃗⃗⃗ ；两边平方可得3=(PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ∵ (PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2≥−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ，∴ 2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32，∴最小值为−32 解法三：配凑法 ∵PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ∴PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(PO ⃗⃗⃗⃗⃗⃗ −PA ⃗⃗⃗⃗⃗⃗ )22=(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(AO ⃗⃗⃗⃗⃗⃗ )22≥−32∴最小值为−323．在∆ABC 中，BC 边上的中线AD 的长为2，点P 是∆ABC 所在平面上的任意一点，则PA PB PA PC ⋅+⋅的最小值为 A ．1B ．2C ．-2D ．-1【详解】建立如图所示的平面直角坐标系，使得点D 在原点处，点A 在y 轴上，则A (0,2)．设点P 的坐标为x y (,)，则(,2),(,)PA x y PO x y =−−=−−， 故()22(2)PA PB PA PC PA PB PC PA PO x y y ⋅+⋅=⋅+=⋅=+−22=+−−≥−x y 2[(1)]2222，当且仅当==x y 0,1时等号成立．所以PA PB PA PC ⋅+⋅的最小值为−2．选C ．4. （武汉二中高二）已知圆M:x 2+(y −1)2=1, 圆N:x 2+(y +1)2=1, 直线l 1、l 2分别过圆心M ,且l 1与圆M 相交于A 、B , l 2与圆N 相交于C 、D , P 是椭圆x 23+y 24=1上的任意一动点, 则PA → ⋅PB → +PC → ⋅PD →的最小值为______________.6 备注：用到极化恒等式5．在平面四边形ABCD 中，===AB BC CD 22，∠ABC =60∘,∠ADC =90∘，若BE →=EF →=FG →=GC →，则2AE →∙DC →+AE →∙AF →=_____；若P 为边BC 上一动点，当PA →∙PC →取最小值时，则cos ∠PDC 的值为_____．解：∵平面四边形ABCD 中，===AB BC CD 22，∠ABC =60∘,∠ADC =90∘，∴△ABC 是边长为2的等边三角， 在Rt △ADC 中，AC =2,CD =1，所以∠ACD =60∘，又BE →=EF →=FG →=GC →， ∴E,F,G 是BC 边的四等分点．如图建立坐标系：则：A(0,√3),B (−1,0),C (1,0)， D (32,√32),E (−12,0),F (0,0),G (12,0)， 所以2AE →DC →+AE →AF →=2(−12,−√3)(−12,−√32)+(−12,−√3)(0,−√3)=132，再设P (x,0)，则−1≤x ≤1，∴PA →PC →=(−x,√3)(1−x,0)=x 2−x =(x −12)2−14，显然x =12时，PA →PC →最小，此时P (12，0)，∴cos ∠PDC =cos ⟨DP →，DC →⟩=(−1，−√3)⋅(−1，−√3)(−1)+(−√32)(−12)+(−√32)=5√714．故答案为：132，5√714．6．在△OAB 中，OA =OB =2，AB =2√3，动点P 位于直线OA 上，当PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值时，向量PA ⃗⃗⃗⃗⃗⃗ 与PB ⃗⃗⃗⃗⃗⃗ 的夹角余弦值为（ ）A ．−3√77B ．7C ．−√217D ．√213【详解】∵|AB ⃗⃗⃗⃗⃗⃗ |2=(OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗⃗ )2=OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ ，即8−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =12，∴OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =−2， 设OP ⃗⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗⃗ (0≤λ≤1)，PA ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ，PB ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −OP ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ ， 所以，PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅(OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ )=(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ +λ(λ−1)OA⃗⃗⃗⃗⃗⃗ 2 =−2(1−λ)+4λ(λ−1)=4λ2−2λ−2=(2λ−12)2−94，当λ=14时，PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值−94，此时|PA ⃗⃗⃗⃗⃗⃗ |=34|OA ⃗⃗⃗⃗⃗⃗ |=32， |PB ⃗⃗⃗⃗⃗⃗ |2=|OB ⃗⃗⃗⃗⃗⃗ −14OA⃗⃗⃗⃗⃗⃗ |2=116OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−12OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =116×22+22−12×(−2)=214，所以，|PB ⃗⃗⃗⃗⃗⃗ |=√212，则cos <PA⃗⃗⃗⃗⃗⃗ ,PB ⃗⃗⃗⃗⃗⃗ >=PA⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ |PA⃗⃗⃗⃗⃗⃗ |⋅|PB ⃗⃗⃗⃗⃗⃗ |=−9432×√212=−√217. 故选：C.7. （三星）在锐角∆ABC 中已知B= 3，|AB ⃗⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ |=2,则AB ⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 的取值范围是__________.解：法一：极化恒等式；法二：以B 为原点，BA 所在直线为x 轴建立坐标系，因为设A（x ，0）因为△ABC 是锐角三角形，所以A+C=120°，∴30°＜A ＜90°，即A 在如图的线段DE 上（不与D ，E 重合），所以1＜x ＜4，则AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ =x 2﹣x=（x ﹣12）2﹣14，所以AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ 的范围为（0，12）．方法2∵∠B=π3， △ABC 是锐角三角形，所以A+C=120°，∴30°＜A ＜90°=a=2由正弦定理可得()−==A B a b csin 120sinA sin 0∴=b ,=−Ac A sin 2sin 1200)( ∴120cos cos AB AC c b A A ===+=+⎝⎭−AA Asin tan 32202)(∵∈tanA0,3)( ∴(0,12AB AC ∈)8.在△ABC 中，AC ＝2BC ＝4，∠ACB 为钝角，M ，N 是边AB 上的两个动点，且MN ＝1，若CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ 的最小值为34，则cos ∠ACB ＝ ． 【答案】1−3√58【解析】取MN 的中点P ，则由极化恒等式得CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ =|CP ⃗⃗⃗⃗⃗ |2−14|MN ⃗⃗⃗⃗⃗⃗⃗ |2=|CP ⃗⃗⃗⃗⃗ |2−14∵CM ⃗⃗⃗⃗⃗⃗ ⋅CN ⃗⃗⃗⃗⃗⃗ 的最小值为34∴|CP ⃗⃗⃗⃗⃗ |min 由平几知识知：当CP ⊥AB 时，CP 最小. 如图，作CH ⊥AB ，H 为垂足，则CH=1 又AC ＝2BC ＝4，所以∠B ＝30o ，sinA=14 所以cos ∠ACB ＝cos （150o －A ）=1−3√58.9.如图所示，矩形ABCD 的边AB=4，AD=2，以点C 为圆心，CB 为半径的圆与CD 交于点E ，若点P 是圆弧EB ̂ (含端点B 、E)上的一点，则PA → ·PB → 的取值范围是 .H【解析】取AB 的中点设为O ，则， 当O 、P 、C 共线时， PO 取得最小值为PO =2√2−2；当P 与B （或E ）重合时，PO 取得最大值为PO=2， 所以的取值范围是.10.如图，是边长为P 是以C 为圆心，1为半径的圆上的任意一点，则AP⃗⃗⃗⃗⃗⃗ ∙BP ⃗⃗⃗⃗⃗⃗ 最小值是_____.－111.（三星）如图，在△ABC 中，D 是BC 的中点，E,F 是AD 上的两个三等分点，BA ⃗⃗⃗⃗⃗⃗ ⋅CA ⃗⃗⃗⃗⃗ =4,BF ⃗⃗⃗⃗⃗⃗ ⋅CF ⃗⃗⃗⃗⃗ =−1,则BE ⃗⃗⃗⃗⃗⃗ ⋅CE ⃗⃗⃗⃗⃗ 的值是________.备注：极化恒等式的典型应用2221=4PA PB PO AB PO ⋅−=−4PA PB ⋅−[8∆ABC CA BP12.若平面向量a ，b 满足|2a －b|≤3，则a·b 的最小值为________.【解析】根据极化恒等式得：8a ⋅b =(2a +b)2−(2a −b)2=(2a +b)2−9≥−9，故a ⋅b ≥−98，所以a ⋅b 的最小值为−98．13.已知平面向量a ，b ，e 满足|e|＝1，a·e ＝1，b·e ＝－2，|a ＋b|＝2，那么a·b 的最大值为________． 解： 由a·e ＝1，b·e ＝－2得: a·e －b·e ＝3，即（a －b ）·e ＝3，|a －b|cos θ＝3a·b=14[|a ＋b|2－|a －b|2]≤－5414.在中，已知，，则面积的最大值是 ．解：取BC 的中点为D ，则AB ⃗⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =AD 2−BC24，所以AD =√2因为BC 边上的高线长不大于中线长，当中线就是高线时，面积最大，故．15.已知平面向量a ⃗ ,b ⃗ ,c ⃗ 满足|a ⃗ |=1，a ⃗ ⋅b ⃗ =12，a ⃗ ⋅c ⃗ =2，|2b ⃗ −c ⃗ |=2，那么b⃗ ⋅c ⃗ 的最小值为________． 【解析】由a ⃗ ⋅b ⃗ =12，a ⃗ ⋅c ⃗ =2得2a ⃗ ⋅b ⃗ +a ⃗ ⋅c ⃗ =3，即a ⃗ ⋅(2b ⃗ +c ⃗ )=3 又a ⃗ ⋅(2b ⃗ +c ⃗ )=|a ⃗ ||2b ⃗ +c ⃗ |cos θ（其中θ为向量a ⃗ 与2b ⃗ +c ⃗ 的夹角） 所以|2b⃗ +c ⃗ |=3cos θ所以b⃗ ⋅c ⃗ =18[(2b ⃗ +c ⃗ )2−(2b ⃗ −c ⃗ )2]=18(9cos 2θ−4)≥58.∆ABC =BC 21AB AC •=∆ABC ∆ABC16.已知锐角的外接圆的半径为1， ，则的取值范围为__________．17.已知正三角形ABC 内接于半径为2的圆O ，点P 是圆O 上的一个动点，则PA → ⋅PB →的取值范围是_____.[－2,6]18.在ΔABC 中，AB =3,AC =4,∠BAC =60°，若P 是ΔABC 所在平面内的一点，且AP =2，则PB → ⋅PC →的最大值为_____.10+2√3719.已知点P 是边长为2√3的正三角形ABC 内切圆上的一点，则PA → ⋅PB →的取值范围为_____.[−3,6]20.已知正方形ABCD 的边长为1，中心为O ，直线l 经过中心O ，交AB 于点M ，交CD 于点N ，P 为平面上一点，若2OP → ＝λOB → ＋(1－λ)OC → ，则PM → ·PN →的最小值为__________.−71621.设点P 为正三角形△ABC 的边BC 上的一个动点，当PA → ·PC →取得最小值时，sin ∠PAC 的值为________．√392622.在平面直角坐标系xOy 中，点A ，B 分别在x 轴，y 轴正半轴上移动，AB ＝2，若点P 满足PA → ·PB →＝2，则OP 的取值范围为________．[√3−1,√3+1]23.在△ABC 中，E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则PB → ·PC →＋BC →2的最小值是__________．4√3∆ABC ∠=πB 6BA BC⋅⎝ ⎛23,3。
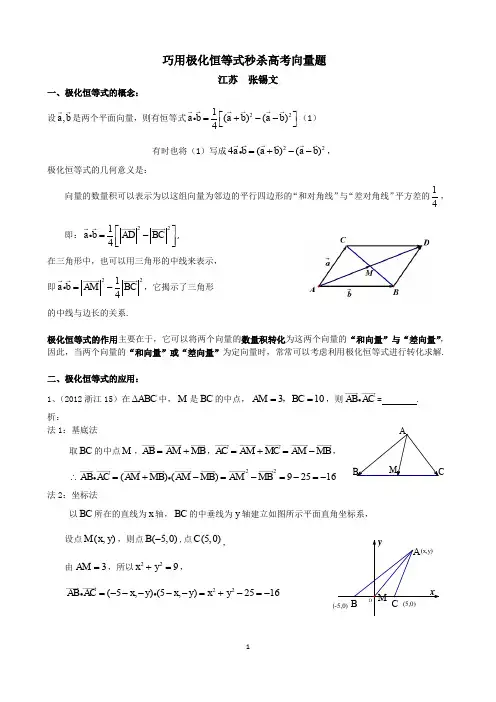
极化恒等式【一.式子结构分析】 1.()2222a ba ab b +=++r r r r r r ，同理可以有：()2222a ba ab b -=-+r r r r r r .两个式子相加可得：()()()22222a b a ba b +=++-r rr r r r ,这个说明平行四边形对角线的平方和等于四边的平方和，也等于邻边的平方和的两倍，由此可得三角形的中线长公式：a m =本20页）. 2.()2222a ba ab b +=++r r r r r r ，同理可以有：()2222a ba ab b -=-+r r r r r r .两个式子相减可得：()()224a ba b a b +--⋅=r r r r rr ,这个叫极化恒等式，2017年全国甲卷理科选择最后一题考查了.3. 很多时候我们也会遇到22a b -r r 这样的式子，一般22()()a b a b a b -+=-r r r r r r ，类似于平方差公式，实质上同2差不多【二、极化恒等式】和数学上很多经典的公式定理一样，极化恒等式也并没有那么神秘，甚至说是很基本. 回忆必修四105页例2()2222a ba ab b +=++r r r r r r ，同理可以有：()2222a ba ab b -=-+r r r r r r .两个式子相加可得：()()()22222a b a ba b +=++-r rr r r r ,这个说明平行四边形对角线的平方和等于四边的平方和，也等于邻边的平方和的两倍，由此可得三角形的中线长公式：a m =本20页）.两个式子相减可得：()()224a ba b a b +--⋅=r r r r rr ,这个叫极化恒等式，2017年全国甲卷理科选择最后一题考查了.极化恒等式的几何意义是:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14，即221()4a b AD BC ⋅=-r r .在三角形中，也可以用三角形的中线来表示，即2214a b AM BC ⋅=-r r ，他揭示了三角形的中线与边长的关系.下面通过几道题目，来分析极化恒等式的妙用.4. 在ABC ∆中，M 是BC 的中点，3,10AM BC ==，则AB AC ⋅=u u u r u u u r________.解析： ()22()4AB ACAB AC AB AC +-⋅=-u u u r u u u r u u u r u u u r u u u r u u u r224BC AM -=u u u ru u u u r 16=- 事实上，类似的问题时有看到，只是很多时候用其他的方法取代了“极化恒等式”，或在无意中使用“极化恒等式”.在ABC ∆中，D 是BC 的中点，2,3AB AC ==，则AD BC ⋅=u u u r u u u r________.解析： ()()2AB ACAD BC AB AC +⋅=⋅-u u u r u u u r u u u r u u u ru u u r u u u r 221()2ABAC =-u u ur u u u r 52=.5. 在Rt △ABC 中，CA ＝CB ＝3，M ，N 是斜边AB上的两个动点，且MN =CM CN u u u u r u u u rg的取值范围为_______.解析：设MN 的中点为D ，则()()2214CM CN CM CN CM CN ⎡⎤=+--⎢⎥⎣⎦u u u u r u u u r u u u u r u u u ru u u u r u u u r g()[]22241124,26CD MN CD ⎡⎤=-=-⎢⎥⎣⎦∈u u u r u u u u r u u u r 类题：△ABC 中，AC ⊥BC ，AB ＝3，AC ＝1，D 为BC 的中点，F 为线段AD 上任意一点，求()AF FB FC+u u u r u u u r u u u rg 的最大值.解析：()22AF FB FC AF FD AF FD +==u u u r u u u r u u u r u u u r u u u rg gg ，因AF FD AD +==，故当AF FD ==()AF FB FC +u u u r u u u r u u u r g 取最大值32.6. （2017年高考全国卷Ⅱ理12）已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+u u u r u u u r u u u r的最小值是A.2-B.32-C. 43- D.1- 解法分析思路一：建系，将向量运算坐标化解法1：如图1，建立平面直角坐标系xOy，(A ，()1,0B -，()1,0C ，设(),P x y ，则()PA x y =-u u u r，()()()1,1,2,2PB PC x y x y x y +=---+--=--u u u r u u u r ，所以()(2223322222PA PB PC x y y x y ⎡⎤⎛⎢⎥+=+-=+-- ⎢⎥⎝⎭⎦≥⎣u u u r u u u r u u u r g ， 当且仅当0x =，2y =，即P 为AO 的中点时取等号，则所求最小值为32-，选B.图1思路二：取BC 中点M ，将PB PC +u u u r u u u r 转化为2PM u u u u r ，则()22PA PB PC PA PM PA PM +==u u u r u u u r u u u r u u u r u u u u r u u u r u u u u rg g g ，怎么求PA PM u u u r u u u u rg 的最小值呢？如图2，设AM 的中点为N ，则()()()()22222113324444PA PM PA PM PA PM PN MA PN ⎡⎤⎡⎤=+--=-=--⎢⎥⎢⎥⎣⎦⎣≥⎦u u u r u u u u r u u u r u u u u r u u u r u u u u r u u u r u u u r u u u r g ，当且仅当20PN =u u u r ，即P 与N 重合（P 为AM 的中点）时取等号，故PA PM u u u r u u u u r g 的最小值为34-，所求最小值为33242⎛⎫⨯-=- ⎪⎝⎭，选B. 注：（1）转化PA PM u u u r u u u u r g 时用到了极化恒等式()()2214PA PM PA PM PA PM⎡⎤=+--⎢⎥⎣⎦u u u r u u u u r u u u r u u u u r u u u r u u u u r g ，其一般形式为()()2214a b a b a b ⎡⎤=+--⎢⎥⎣⎦r r r r r r g ；（2）PA PM u u u r u u u u r g 也可这样转化： PA PM =u u u r u u u u r g ()()PN NA PN NM ++u u u r u u u r u u u r u u u u r g ()()PN NA PN NA =+-u u u r u u u r u u u r u u u r g 22234PN NA PN =-=-u u u r u u u r u u u r .图2类题：已知动点M 是腰长为2的等腰直角三角形ABC ∆（C ∠为直角）的三边上的动点，则(+)MA MB MC ⋅u u u r u u u r u u u u r的取值范围是（ ）A ．1[,0]2- B ．[0,4] C ．1[,4]2-D．答案：C解析：取AB 中点D ，CD 中点E ，则(+)MA MB MC ⋅u u u r u u u r u u u u r2MD MC =⋅u u u u r u u u u r()()22124MD MCMD MC ⎡⎤=⨯+--⎢⎥⎣⎦u u u ur u u u u r u u u u r u u u u r 22214212ME CD ME ⎡⎤=-=-⎢⎥⎣⎦u u u r u u u r u u u r7. ***如图，在凸四边形ABCD 中，66AB AD BD ⋅==u u u r u u u r ，，O 是BD 的中点，且3AO OC =u u u r u u u r，则CB CD ⋅u u u r u u u r等于（ ）A ．115- B ．89-C ．223-D ．83解析：22(+)()4AB AD AB AD AB AD --⋅=u u u r u u u r u u u r u u u r u u u r u u u r 222494AO DB AO -==-u u u r u u u ru u u r 6=22(+)()4CB CD CB CD CB CD --⋅=u u u r u u u r u u u r u u u ru u u r u u u r 29CO =-u u u r 223=-.8. ***（2013年浙江高考理）ABC ∆中0P 是边AB 上一定点，满足014P B AB =，且对于边AB 上任取的一点P ，恒有00PB PC P B PC ⋅≥⋅u u u r u u u r u u u r u u u r，则( )A ．B ．C ．D ．【答案】D解析： 法1：【将式子转化为与某一个变量有关系的式子，即函数式.由已知条件，当14PB AB =时，函数式子取最大值】设,PB x BC a ==，作CH AB ⊥，则cos BH a B =.则22()cos PB PC PB PB BC PB BP BC x xa B ⋅=⋅+=-⋅=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r由题意，当且仅当111cos 224x a B BH AB ===时，上式 有最小值.此时，H 也为AB 的中点，故AC BC =.法2：由题意，设|→AB |=4，则|→P 0B |=1，过点C 作AB 的垂线，垂足为H ，在AB 上任取一点P ，设HP 0=a ，则由数量积的几何意义可得，→PB ∙→PC =|→PH ||→PB |=(|→PB | −(a +1))|→PB |，→P 0B ∙→P 0C =−|→P 0H ||→P 0B |=−a ，于是→PB ∙→PC ≥→P 0B ∙→P 0C 恒成立，相当于(|→PB |−(a +1))|→PB |≥−a 恒成立，整理得|→PB |2−(a +1)|→PB |+a ≥0恒成立，只需∆=(a +1)2−4a =(a −1)2≤0即可，于是a =1，因此我们得到HB =2，即H 是AB 的中点，故△ABC 是等腰三角形，所以AC =BC法3：如图建系，设(,0),(,),(,0)C C B b C x y P x ， 2()CCPB PC x b x x bx ⋅=-++u u u r u u u r ，当且仅当24C b x b x +==时，上式取最小值，此时2C bx =，故AC BC =. 法4：以AB 中点为坐标原点建系也可，同法2.法5: 极化恒等式 224=()()a b a b a b ⋅+--r r r r r r如图，取线段BC 的中点M ，则22224=()()4PB PC PB PC PB PC PM BC ⋅+--=-u u u r u u u r u u u r u u u r u u u r u u u r ， 要使得4PB PC ⋅u u u r u u u r 的值最小，只需24PM u u u u r 取最小值.因为P 是线段AB 上动点，所以只有当PM AB⊥时，PM u u u u r取得最小值，且点P 与点0P 必须重合，M 是线段BC 的中点，只有AC=BC 时才能成立.090=∠ABC 090=∠BAC AC AB =BC AC =CBAHC BAxPy9. ***（2012年安徽卷）若平面向量,a b r r 满足23a b -r r≤，则a b ⋅r r 的最小值是_________.解析：2212(2)(2)4a b a b a b ⎡⎤⋅=+--⎣⎦r r r r r r 219(2)44a b ---r r ≥≥.所以98a b ⋅-r r ≥.A.32+ B. 12+ C. 322+ D. 122+解：法1：全部与圆心联系起来，基本定义设AB 中点为D ，=()()PA PB PO OA PO OB ⋅+⋅+u u u r u u u r u u u r u u u r u u u r u uu r22PO PO OD OA OB =+⋅+⋅u u u r u u u r u u u r u u u r u u u r1122PO OD =+⋅+u u u r u u ur 3,2PO OD =<>u u u r u u u r，∵cos ,[1,1]PO OD <>∈-u u u r u u u r ，∴PA PB ⋅u u u r u u u r的范围为33[22.法2：建立坐标系，需要用到辅助角公式以O 点为原点，OA 为x 轴建立平面直角坐标系，则1(1,0),(,)22A B ， （也可设点11),)22A B -） 设(cos ,sin ),02P αααπ≤<，则1(1cos ,sin ),(cos sin ),2PA PB αααα=--=--u u u r u u u r 1(1cos )(cos )(sin sin )2PA PB αααα⋅=--+--u u u ru u u r33cos 222αα=--313(sin )222αα=+3)23πα=+∵1sin()13πα-≤+≤，∴333)2232πα≤+≤，故PA PB ⋅u u u r u u u r 的范围为33[3,3]22-+.法3：建立坐标系，设点3131(,),(,)22A B -，(,)P x y ， 332PA PB x ⋅=-u u u r u u u r法4：转化为求三角形的面积的最大值，使用余弦定理和基本不等式cos cos30PA PB PA PB APB PA PB ⋅=⋅∠=⋅u u u r u u u r u u u r u u u r u u u r u u u r 32PA PB =⋅u u u r u u u r ， 根据余弦定理和基本不等式2220cos302PA PB AB PA PB +-⋅=u u u r u u u r 12PA PB ⋅-≥， 法5：转化为求三角形的面积的最大值，使用余弦定理和基本不等式求32PA PB ⋅u u ur u u u r 的最大值也即求三角形的面积的最大值，也即求点 P 到AB 距离的最大值 法6：与三角形中点联系起来设AB 中点为D ， 则=()()PA PB PD DA PD DB ⋅+⋅+u u u r u u u r u u u r u u u r u u u r u u u r =()()PD DA PD DA +⋅-u u u r u u u r u u u r u u u r22214PD DA PD =-=-u u u r u u u r u u u r易知，PD u u u r 的范围是33[1,1]-+，故PA PB ⋅u u u r u u u r 的范围为33[3,3]22-+.11. ***（2011年浙江卷）已知直线AB 与抛物线24y x =交于点,A B ，点M 为AB 的中点，C 为抛物线上一个动点，若0C 满足{}00min C A C B CA CB ⋅=⋅u u u u r u u u u r u u r u u u r，则下列一定成立的是（ ）A.0C M AB ⊥B.0C M l ⊥u u u u u r，其中l 是抛物线过0C 的切线C.00C A C B ⊥D.0C M AB = 答案 D解析 如图所示，极化恒等式 CA →·CB →＝(AM →－CM →)·(BM →－CM →)＝CM →2－(BM →＋AM →)·CM →＋AM →·BM →＝CM →2－14AB →2，当直线AB 一定时，当且仅当|CM →|取得最小值时，使得CA →·CB →取最小值， 只有当C M ⊥l 时，|CM →|取得最小值，故选D.【注】本题实质上就是求抛物线上一点到其内一点距离的最小值下面用两种方法来证明，法1：几何分析法，只需证明CM 不与l 垂直时，有比CM 还要短的. 这一招太聪明了，如果直接证明CM 最短很不好证. 设过点C '的切线为l ',此时C M '不与l '垂直，作MH l '⊥， 交抛物线于点1C .则1MC MH MC MC '>>>. 法2：求导运算22200()()CM x x y y =-+-2222000022x x x x y y y y =-++-+22222200002222y y x x y y y y ⎛⎫=-++-+ ⎪⎝⎭22222200002222y y x x y y y y ⎛⎫=-++-+ ⎪⎝⎭()f y =300()2(1)20f y y x y y '=+--=时，上式有最小值？？？？【注】此处如何整理出 CM ⊥CA 时，0011y y x x y-⋅=--，整理得3002(1)20y x y y +--=，两条件相同. 12. 已知圆O 的半径为2，,P Q 是圆O 上任意两点，且060POQ ∠=，AB 是圆O 的一条直径，若点C满足(1)OC OP OQ λλ=-+u u u r u u u r u u u r，则CA CB ⋅u u r u u u r 的最小值是（ ） A ．1- B ．2- C ．3- D ．4-解析：由(1)OC OP OQ λλ=-+u u u r u u u r u u u r 得，点C 在PQ 上，24CA CB CO ⋅=-u u r u u u r易得当且仅当C 为PQ 中点时，CO 有最小值1-.变式：已知圆O 的半径为2，,P Q 是圆O 上任意两点，且060POQ ∠=，AB 是圆O 的一条直径，若点C 满足(1)OC OP OQ λλ=-+u u u r u u u r u u u r，则CA CB ⋅u u r u u u r 的最小值是（ ）A ．1-B ．2-C ．3-D ．4-解析：设OP OP '=-u u u r u u u r ，所以(1)(1)OC OP OQ OP OQ λλλλ'=-+=-+u u u r u u u r u u u r u u u r u u u r， 点C 在P Q '上，24CA CB CO ⋅=-u u r u u u r易得当且仅当C 为PQ 中点时，CO 有最小值3-. 【三. 三角形向量中线公式和中点转化】13. ***点O 是ABC ∆的三边中垂线的交点，a ，b ，c 是角A ，B ，C 的对边，已知2220,13b b c b -+=<<，则BC AO u u u r u u u rg 的范围是____________．解析：O 是ABC ∆的外心，设BC 中点为M ，则OM BC ⊥()BC AO BC AM MO BC AM u u u r u u u r u u u r u u u u r u u u u r u u u r u u u u r g g g =+=2211()()()22AC AB AC AB b c u u u r u u u r u u u r u u u r g =-+=-2b b =-.因为2220b b c -+=，所以2220c b b =->，所以02b <<，又13b <<，所以12b <<.所以BC AO u u u r u u u rg 的范围是（0，2）.14. 已知圆22:1C x y +=，点00(,)P x y 是直线:3240l x y +-=上的动点，若在圆C 上总存在两个不同的点,A B ，使OA OB OP +=u u u r u u u r u u u r，则0x 的取值范围是（ ）A ．24(0,)13B ．24(,0)13- C ．13(0,)24 D ．13(0,)12 答案：A【解析】法1：如图，∵OA OB OP +=u u u r u u u r u u u r；∴OP 与AB 互相垂直平分，∴圆心到直线AB 的距离122020<+y x ；∴42020<+y x ①； 又042300=-+y x ；∴00232x y -=， 代入①得：4232202<⎪⎭⎫ ⎝⎛-+x x ；解得132400<<x ；∴0x 的取值范围是24(0,)13．故选：A ．法2：OP=2时，是临界状态，求出即可.15. ***在ABC ∆中，D 是BC 边上任意一点（D 与B ，C 不重合），且22+AB AD BD DC =⋅，则ABC∆一定是（ ）A ．直角三角形B ．锐角三角形C ．等腰三角形D ．等边三角形解析：类似于平方差公式，22AB AD -表示成向量的平方22AB AD -u u u r u u u r ，可以转化运算 22+AB AD BD DC =⋅u u u r u u u r u u u r u u u r ,220AB AD BD DC --⋅=u u u r u u u r u u u r u u u r ,()0DB AB AC ⋅+=u u u r u u u r u u u r，故是等腰，选C.16. （1）已知圆直径=6AB ，O 点为圆心，C 为半径上不同于A 、B 的任意一点，若P 为半径OC 上的动点，(+)PA PB PC ⋅u u u r u u u r u u u r的最小值是_________.解：(+)2PA PB PC PO PC ⋅=⋅u u u r u u u r u u u r u u u r u u u r 262PO PO =-+92-≥.（2）已知圆半径为1，圆上的弦AB 长为1，P 为圆上的动点，PA PB ⋅u u u r u u u r的最大值是（ ）A.332+ B. 132+ C. 332+ D. 132+ 解： 设AB 中点为D ， 则=()()PA PB PD DA PD DB ⋅+⋅+u u u r u u u r u u u r u u u r u u u r u u u r =()()PD DA PD DA +⋅-u u u r u u u r u u u r u u u r22214PD DA PD =-=-u u u r u u u r u u u r易知，PD u u u r 的范围是33[1,1]-+，故PA PB ⋅u u u r u u u r 的范围为33[3,3]22-+. 17. （1）已知直角梯形ABCD ，AD ∥BC ，090BAD ∠=，AD=2，BC=1，P 是腰AB 上的动点，则+PC PD u u u r u u u r的最小值为_____. 法1：建系，设(0,)P b法2：取CD 中点Q ，+2PC PD PQ =u u u r u u u r，易得P 是AB 的中点时取最小.（2）已知点A ，B ，C 在圆221x y +=上运动，且AB BC ⊥，若点P 的坐标为(2,0)，则PA PB PC ++u u u r u u u r u u u r的最大值为（ ）A.6B.7C.8D.9 【答案】B.法2：因AB BC ⊥，所以AC 为直径，O 为AC 中点，2PA PB PC PO PB ++=+u u u r u u u r u u u r u u u r u u u r，当(1,0)B -时，最大，为7.18. ***如图，在梯形ABCD 中，CD AB //，2=AB ，4=CD ，5==AD BC ，E ，F 分别是AD ，BC 的中点，对于常数λ，在梯形ABCD 的四条边上恰有8个不同的点P ，使得λ=⋅PF PE 成立，则实数λ的取值范围是（ ）A ．)209,45(-- B ．)411,45(- C ．)411,41(- D ．)41,209(-- 答案：D【解析】法1：以CD 中点为坐标原点，CD 所在直线为x 轴建立直角坐标系， 则33(1,2),(1,2),(2,0),(2,0),(,1),F(,1)22A B C D E ---，当P 在CD 边上时，设(,0),||(0,2)P x x ∈，则25511(,)444PE PF x λ=⋅=-∈-u u u r u u u r，对应值都有两个；当P 在AB 边上时，设(,2),||(0,1)P x x ∈，则2551(,)444PE PF x λ=⋅=-∈--u u u r u u u r ，对应值都有两个；当P 在BC 边上时，设(,42),(1,2)P x x x -∈，则2275124PE PF x x λ=⋅=-+u u u r u u u r ，当91(,)204λ∈--时，每一个λ都有两个x 与之对应； 根据对称性，当P 在AD 边上时，同P 在BC 边上时.综上，若有8个不同的点P ，使得λ=⋅PF PE 成立，则实数λ的取值范围是9151191(,)(,)(,)20444204---=--I ，选D. 法2：（巧取中点转化，极化恒等式）取EF 中点H ，取AB 中点M ，取CD 中点N ，1MH NH == 则()()PE PF PH HE PH HF ⋅=+⋅+u u u r u u u r u u u r u u u r u u u r u u u r 2212PH HE =-u u u r u u u r 2214PH EF =-u u u r u u u r 29=4PH -u u u r ，当P 在AB 边上时，2951=(,)444PE PF PH λ=⋅-∈--u u u r u u u r u u u r ，根据对称性，对应值都有两个；当P 在CD 边上时，29511(,)444PH λ=-∈-u u u r ，根据对称性，对应值都有两个；当P 在AD 边上时，PH 的最小值即H 到AD 的距离，由等积法min 5PH =，又2AH =，当(,2)5PH ∈时，91(,)204λ∈--，对应值都有两个；根据对称性，当P 在AD 边上时，同P 在BC 边上时. 综上，若有8个不同的点P ，使得λ=⋅PF PE 成立，则实数λ的取值范围是9151191(,)(,)(,)20444204---=--I ，选D. 19. 如图，在同一平面内，点P 位于两平行直线l 1，l 2同侧，且P 到l 1，l 2的距离分别为1,3.点M ，N 分别在l 1，l 2上，|PM →＋PN →|＝8，则PM →·PN →的最大值为( ) A ．15 B ．12 C ．10 D ．9 答案 A解析：取MN 中点O ，则()142PO PM PN =+=u u u r u u u ur u u u r ，1OM u u u u r ≥ ()()PM PN PO OM PO ON =++u u u u r u u u r u u u r u u u u r u u u r u u u rg g 22216PO OM OM =-=-u u u r u u u u r u u u u r 22216PO OM OM =-=-u u u r u u u u r u u u u r20. ***已知ABC ∆的面积为2，E,F 是AB ，AC 的中点，P 为直线EF 上任意一点，则2PB PC BC ⋅+u u u r u u u r u u u r 的最小值为（ ）A ．2B ．3C ．23D ．4 解析：法1：巧取中点转化法，极化恒等式取BC 中点D ，设底边BC 的高为h ，则12PD h ≥，22()()PB PC BC PD DB PD DC BC +=+++u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r g g222PD DB BC =-+u u u r u u u r u u u r 2234PD BC =+u u u r u u u r 2222313444PD BC h BC =++u u u r u u u r u u u r ≥==≥ 法2：建立平面直角坐标系(如图所示)，【四、极化恒等式在立体几何中的应用】21. 正方体1111ABCD A B C D -的棱长为2，MN 是它内切球的一条弦（把球面上任意2点之间的线段称为球的弦），P 为正方体表面上的动点，当弦MN 最长时，PM PN ⋅u u u u r u u u r 的最大值为_________.解析：设球心为O ，易得球的半径1R =，2221=(2)14PM PN PO R PO ⋅-=-u u u u r u u u r u u u r u u u r ，易得PO PM PN ⋅u u u u r u u u r 的最大值为2.22. 点P 是棱长为1的正方体1111ABCD A B C D -的底面1111A B C D 上一点，则PA PC ⋅u u u r u u u r 的取值范围是_________.解析：设AC 的中点为M ，224PA PC PM AC ⋅=-u u u r u u u r u u u u r u u u r 242PM =-u u u u r 1,12⎡⎤∈⎢⎥⎣⎦23.24.。
