列联表资料的X2检验

格式：ppt
大小：276.32 KB
文档页数：3

下载文档原格式

第五章 χ2检验

χ2的连续性矫正
由上式计算的 χ2 只是近似地服从连续型随机变量 χ2 分布。在对次数资料迚行χ2 检验利用连续型随机变量χ2分布计算概率时，常常偏高，特别是当自由度为1时，偏差较大。
矫正后的χ2值记为χc2
当自由度大于1时， χ2分布与连续型随机变量
χ2分布相近似，这时，可不作连续性矫正，但要
总和
r1 r2
总和
R1= O11 + O12 R2= O21 + O22
C1= O11 + O21
C2= O12 + O22
T
给药方式与给药效果的2×2列联表给药方式
口服注射
有效
58 64
无效
40 31
总数
98(R1) 95(R2)
有效率
59.2％ 67.4％
总数
122(C1)
71(C2)
193(T)
1.H0 ：给药方式与给药效果相互独立。
HA ：给药方式与给药效果有关联。
2.给出显著水平α＝0.05
3.计算各个理论数 Eij＝Ri×Cj/T=行总数×列总数/总数
E11= R1 × C1/T=61.95 E21= R2 × C1/T=60.05 E12= R1 × C2/T=36.05 E22= R2 × C2/T=34.95
本章内容
一、离散型数据 x2 统计量和 x2分布二、拟合优度检验三、独立性检验
拟合优度检验（吻合度检验）
理论数可以通过一定的理论分布或某种学说推算出。用实际观察数与理论数直接比较，从而得
出两者之间是否吻合，这一类检验称为吻合度检验。
独立性检验
分析两类因子是相互独立还是彼此相关。理论值的推算没有什么理论或学说作依据，这时可假设观察的各属性之间没有关联，然后证明这种无关联的假设是否成立。这种检验称为独立性检验。

第六章 χ2检验

二、计算检验统计量：
2 1 4 1 3
2
2 2 2 2 2 2 2 2 30 38 32 12 19 30 19 9 189 1 0 . 69 112 49 112 68 112 51 112 21 77 49 77 68 77 51 77 21
统计：按照α=0.05的检验水准，拒绝H0，接受H1，差异有统计学意义。专业：结合本例，可以认为三种方法治疗慢性支气管炎的效果不同或不全相同。
2.两组或多组样本构成比的比较
例6-4：欲了解儿童白血病患者的血型分布是否与成年患者有所不同，资料见表6-4。试分析儿童白血病患者与成年患者的血型分布构成比有无差别？
第六章 χ2检验
《医学统计学》余松林主编
本章内容
第三节独立性检验第四节趋势检验第五节多个四格表的联合分析第六节四格表的费歇尔精确概率检验
第三节独立性检验
本节介绍应用χ2检验推断两个或两个以上总体率（或构成比）之间有无差别及两分类变量间有无相关关系。
一、四格表资料的χ2检验（两个样本率的比较）
表6-4 儿童急性白血病患者与成人急性白血病患者的血型分布
分组
儿童成人合计
A型 30
19 49
B型 38
30 68
O型 32
19 51
AB型 12
9 21
合计 112
77 189
解：
一、建立假设，确定检验水准：
H0：儿童白血病患者与成人患者的血型分布构成比相同 H1：儿童白血病患者与成人患者的血型分布构成比不相同检验水准α=0.05。
二、计算检验统计量：

X2检验

X2检验X2检验是用途广泛的假设检验方法，它的原理是检验实际分布和理论分布的吻合程度。

主要用途有：两个及以上样本率（或构成比）之间差异比较，推断两变量间有无相关关系，检验频数分布的拟合优度。

Ｘ2检验类型有：四格表资料Ｘ2检验(用于两样本率的检验)，行×列表Ｘ2检验（用于两个及两个以上样本率或构成比的检验）, 行×列列联表Ｘ2检验（用于计数资料的相关分析）。

在SPSS中，所有X2检验均用Crosstabs完成。

Crosstabls过程用于对计数资料和有序分类资料进行统计描述和统计推断。

在分析时可以产生二维至n维列联表，并计算相应的百分数指标。

统计推断则包括了我们常用的X2检验、Kappa值，分层X2（X2M-H）。

如果安装了相应模块，还可计算n维列联表的确切概率（Fisher's Exact Test）值。

Crosstabs过程不能产生一维频数表（单变量频数表），该功能由Frequencies 过程实现。

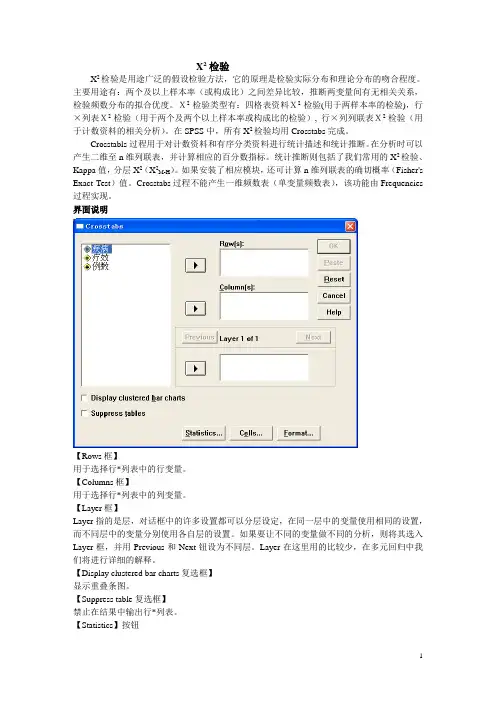
界面说明【Rows框】用于选择行*列表中的行变量。

【Columns框】用于选择行*列表中的列变量。

【Layer框】Layer指的是层，对话框中的许多设置都可以分层设定，在同一层中的变量使用相同的设置，而不同层中的变量分别使用各自层的设置。

如果要让不同的变量做不同的分析，则将其选入Layer框，并用Previous和Next钮设为不同层。

Layer在这里用的比较少，在多元回归中我们将进行详细的解释。

【Display clustered bar charts复选框】显示重叠条图。

【Suppress table复选框】禁止在结果中输出行*列表。

【Statistics】按钮弹出Statistics对话框，用于定义所需计算的统计量。

Chi-square复选框：计算X2值。

Correlations复选框：计算行、列两变量的Pearson相关系数和Spearman等级相关系数。

Norminal复选框组：选择是否输出反映分类资料相关性的指标，很少使用。

x2检验第六版

第二个表显示列联表的资料,一个期望频数小于5（4.8）
皮尔逊卡方值x2（pearson chi-square）
连续校正x2（continuity correction），仅在2×2表计算
似然比值（likelylihood ratio）费歇尔精确检验（fisher‘s exact test）线形组合（linear-by-linear association）有效例数（N of valid cases）
如果想对其中的两个率进行相互比较时，最好能够采用更加复杂的分类数据模型，如对数线性模型或者logistic回归模型进行分析，采用列联表分割等方法只能得到近似的结果，最好不要使用。
四、配对设计
（一）配对设计四格表（2×2列联表）
计数资料配对设计的应用：可用于两种检验方法、培养方法、诊断
有效例数（N of valid cases）
结论：有0个格子的期望频数小于5，最小期望频数为6.56，符合pearson x2检验的要求。
皮尔逊卡方值x2=4.130，p=0.042＜0.05，差别有统计学意义。
四格表校正卡方检验
例题9-3
步骤：
1、定义变量，输入数据设三个变量：处理（r）：即行号状况（c）：即列号频数（f）
Rows框：sex columns框：x0 cells： percentages：选择row、column、total →continue→ok
Cells 按钮
首先是处理记录缺失情况报告，可见24例均为有效值。
第九章 χ2 检验(卡方检验)
χ2检验(chi square test)是以χ2 分布为理论基础的检验方法。主要用于分类资料（列联表资料，contingency table）的假设检验。也用于频数分布的拟合优度检验（goodness of fit）.

X2检验简单教程一学就会

X2检验X2检验是用途广泛的假设检验方法，它的原理是检验实际分布和理论分布的吻合程度。

主要用途有：两个及以上样本率（或构成比）之间差异比较，推断两变量间有无相关关系。

在SPSS中，所有X2检验均用Crosstabs完成。

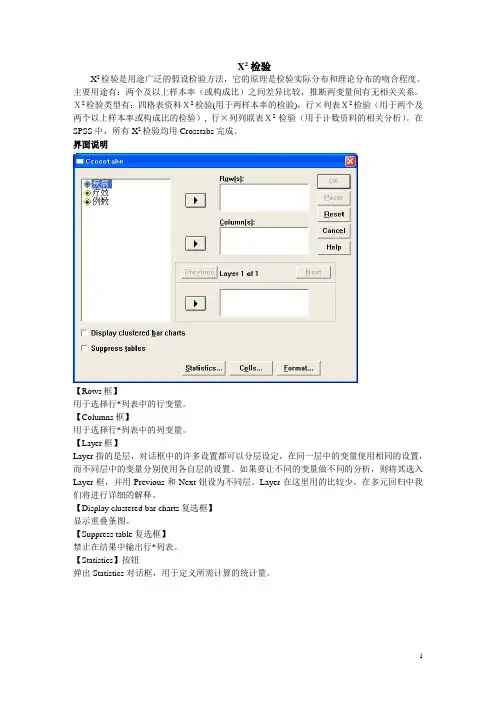
界面说明【Rows框】用于选择行*列表中的行变量。

【Columns框】用于选择行*列表中的列变量。

【Layer框】Layer指的是层，对话框中的许多设置都可以分层设定，在同一层中的变量使用相同的设置，而不同层中的变量分别使用各自层的设置。

如果要让不同的变量做不同的分析，则将其选入Layer框，并用Previous和Next钮设为不同层。

Layer在这里用的比较少，在多元回归中我们将进行详细的解释。

【Display clustered bar charts复选框】显示重叠条图。

【Suppress table复选框】禁止在结果中输出行*列表。

【Statistics】按钮弹出Statistics对话框，用于定义所需计算的统计量。

Chi-square复选框：计算X2值。

Correlations复选框：计算行、列两变量的Pearson相关系数和Spearman等级相关系数。

Norminal复选框组：选择是否输出反映分类资料相关性的指标，很少使用。

Contingency coefficient复选框：即列联系数，其值界于0～1之间；Phi and Cramer's V复选框：这两者也是基于X2值的，Phi在四格表X2检验中界于-1～1之间，在R*C表X2检验中界于0～1之间；Cramer's V 则界于0～1之间；Lambda复选框：在自变量预测中用于反映比例缩减误差，其值为1时表明自变量预测应变量好，为0时表明自变量预测应变量差；Uncertainty coefficient复选框：不确定系数，以熵为标准的比例缩减误差，其值接近1时表明后一变量的信息很大程度来自前一变量，其值接近0时表明后一变量的信息与前一变量无关。

第七章-X2检验(医学统计学)

四格表概率P的计算公式
(a+b)!(c+d)!(a+c)!(b+d)! P＝────────────
a!b!c!d!n!
例8.8
表8.9 两型慢性布氏病的PHA皮试反应 ━━━━━━━━━━━━━━━━━━━
分型阳性数阴性数合计阳性率(%)
───────────────────
活动型 1(2.4) 14(12.6) 15 6.67
18.74
17.26
19.26
17.74
=10.262 ( 1 1 1 1 ) 18.74 17.26 19.26 17.74
＝23.12
(2) 用专用公式计算
a=29、b=7、c=9 、d=28 、n=73
x2
(ad bc)2 n
(a b)(c d )(a c)(b d )
(29 28 7 9)2 73 23.12 36 37 38 35
3、查X2 界值表确定P值按＝1，查附表8，X2界值表得：
X20.05，1=3.84、 X20.01，1=6.63 、X20.005，1=7.88 X2 >7.88, P<0.005
4、推断结论 P<0.005, 按α＝0.05，拒绝H0，接受H1，可认
为两总体阳性率有差别，铅中毒病人尿棕色素阳
x2
大。
可以根据X2分布原理，由X2值确定P值，从而作出推论。
V=(行数-1)(列数-1)
四格表资料X2检验专用公式：
x2
(ad bc)2 n
(a b)(c d )(a c)(b d )
式中：a、b、c、d为四个实际数，其中 a、c 为阳性数，b、d 为阴性数，n 为总例数。

x2检验

4. 进行假设检验。如图所示，分别输入置信水平、临界值和假设检验的结果。其中CHIINV 函数的自由度 =(第一类属性的分类数-1)*( 第二类属性的分类数1)=(3-1)*(4-1)=6。
B15 单元格的卡方概率值1.3E-07与B24 单元格的卡方统计量 42.748是表格的两个重要计算结果。 1、得到以上观察的样本的概率是0.00000013。这个概率几乎接近于0，拒绝H0，所以可以认为总体的这两个属性不是独立的，是显著相关的。 2、卡方统计量42.748，显著水平为0.01时的卡方临界值是 16.8117，所以P<0.01，同样拒绝H0，得出同样的结论
理论数(Ei) 312.75(E1) 104.25(E2) 104.25(E3) 34.75(E4) 556 问此豌豆性状的比率是否符合遗传分离定律的9∶3∶3∶1比例
解：理论数均大于5，df=3
315 312.752 101 104.252 108 104.252 32 34.752 2
2 =0.893+2.949=3.932 H0: O－T=0, α=0.05, df=1, 2 0.05=3.841， 2 > 2 0.05
结论：正常翅与残翅的分离比不符合3∶1
（2）矫正正常翅残翅
∣O－T∣－0.5 （ ∣O－T∣－0.5 ）2 （ ∣O－T∣ 36.05 0.192 0.330 0.198 0.341 1.061
02.05 3.841, 2 02.05 , P 0.05
结论：接受H0，不同给药方式的治疗效果没有显著不同。
r×c列联表
例6.3称为2×2列联表，虽然在生物学问题中，经常遇到的是2×2列联表，对于行、列大于2的情况称为r×c列联表。其理论数的计算与2×2列联表相同： df=(r-1)(c-1)

第09章 X2检验

第9章 X2检验9.1 列联表统计分析1、列联表统计分析过程例9.1在二乙基亚硝胺诱发大白鼠咽癌的实验中，一组单纯用亚硝胺向鼻腔内滴注；另一组在鼻注的基础上加肌注维生素B12，问两组发癌率的差别有无统计意义。

实验结果如表9.1所示。

表9.1大白鼠鼻回癌的实验数据━━━━━━━━━━━━━━━━━━发癌数未发癌数━━━━━━━━━━━━━━━━━━鼻注组 52 19鼻注加肌注组 39 3━━━━━━━━━━━━━━━━━━本例为两样本率之间的比较，可以采用x2检验进行分析。

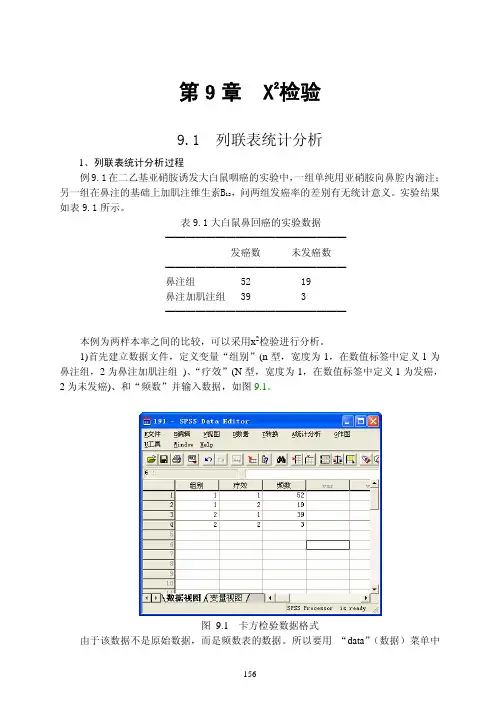
1)首先建立数据文件，定义变量“组别”(n型，宽度为1，在数值标签中定义1为鼻注组，2为鼻注加肌注组)、“疗效”(N型，宽度为1，在数值标签中定义1为发癌，2为未发癌)、和“频数”并输入数据，如图9.1。

图 9.1 卡方检验数据格式由于该数据不是原始数据，而是频数表的数据。

所以要用“data”（数据）菜单中的weight cases（案例加权）来进行加权处理。

2)、单击Data（数据）菜单中的Weight Cases（案例加权）子菜单，弹出Weight Cases （案例加权）对话框，将“频数”变量单击进入Frequency Variable（频数变量）框内，按“频数”对数据进行加权，此时所有观测值相当于发生了“频数”次，如图9.1.2，单击Continue按钮返回主对话框。

图 9.2 案例加权3)、执行Analyze（统计分析）菜单|Descriptive Statistics（描述统计量）子菜单|Crosstabs…（交叉表）命令，系统弹出Crosstabs（交叉表）对话框，如图9.1.3，图 9.3交叉表对话框(1)单击变量从变量清单中选择1个（组别）或几个变量进入Row(s)（行）框中，作为交叉表的行，选择1个（疗效）或几个变量进入Column(s)（列）框中，作为交叉表的列，表示以“组别”变量为交叉表的行，以“疗效”为交叉表的列。

卫生统计学9——卡方检验

因此， ★ 对实际数与理论数差值的假设检验等价于对两样
本率差值的假设检验
14
2 (A T )2
T
15
由χ2 的计算可见， χ2 检验的基本思想是：
Χ2值反映了实际数与理论数相吻合的程度。如果检验假设H0成立，则A=T，现A≠ T 可能原因（1）抽样误差造成
（2）来自不同总体若为（1），则A与T差别不会很大，出现大的Χ2值的可能性很小，当p≤ α,就怀疑假设H0，因而拒绝；反之，当 p>α,则无理由拒绝。
统计量2值。
33
计算统计量:
计算T I 时的参数有2 个（均数和标准差）
2
(A T )2 6.27
T
推断结论:自由度=10-1-2=7,
查附表8,得到
2 0.50,7
6.35
P>0.50,可以认为该样本服从正态分布。
34
例调查者欲观察某克山病区克山病患者的空间分布，将该区划分为279个取样单位，统计各取样单位历年累计病例数，资料见下表第(1)、(2) 栏，问此资料是否服从Poisson分布？
在上例中， 64 21 的数据是基本的，
51 33
其余数据都是由以上四个数据计算出来的。
这四个数叫实际频数，简称实际数
（actual freqency, A）
12
理论频数（theoretical freqency,T）
对于洛赛克组的64人，按照合并愈合率Pc=68.05%治疗的话，理论上: 64×68.05%=57.84人愈合，用T11表示，
18
3、查χ2界值表，确定P值，作出结论查 P482 附表8
根据自由度和事先确定的检验水准，
查得对应的χ2界值。作出判断结论，

007 第七章 X2检验

表7-4 两种方法检验结果甲法(病理) ＋＋－合计 130(a) 11（c） 141 乙法（超声）－ 75（b） 41 (d) 116 205 52 257 合计
这是配对设计计数资料，表中两法的差别是由b和 c 两格数据来反映。总体中 b 和 c 对应的数据可用 B 和C 表示。
配对X2检验计算公式：
合
计
H0 :胃十二指肠疾病患者与健康输血员血型总体构成比相同 H1 :胃十二指肠疾病患者与健康输血员血型总体构成比不同 α=0.05 按公式
有效率（%）
治疗组对照组合计
200 190 390 160 148
160 148 308 160 148
80.00 77.89 78.97 40 42
200 190
二、X2检验基本思想 X2 值的计算方法（通用公式）：
2 ( A T ) x2 T
式中A为实际数，T为理论数，是根据H0的假设推算出来。
2 ( b c ) x2 , v 1 bc
若b+c<40:
2 (| b c | 1) x2 , v 1 bc
H0：两种方法总体检出率相等，即B=C； H1：两种方法总体检出率不相等，即B≠C； α=0.05
2 2 ( b c ) (75 11) x2 47.63 bc 75 11
疗法阴转人数未阴转人数合计阴转率(%)
───────────────────────────── 甲 30 14 44 68.2 乙 9 36 45 20.0 丙 32 12 44 72.7 ───────────────────────────── 合计 71 62 133 53.4 ━━━━━━━━━━━━━━━━━━━━━

第八章 x2检验

实际频数A (actual frequency) ( a、b、c、d) 理论频数T ( theoretical frequency)
2检验的基本思想:
(A T) 基本公式： T
2 2
式中A代表每个格子的实际频数( actual
frequency )，即表中的基本数据；T代表每个格子的
(三）四格表专用公式
当总例数n≥40且所有格子的T ≥5时, 可用χ2检验的基本公式，也可用下面的专用公式：
(ad bc) n (a b)(c d )(a c)(b d )
2 2
1
疗法盐酸苯乙双胍安慰剂合计
பைடு நூலகம்
死亡 26 (a) 2 (c) 28 (a+c.)
3.R×C列联表的分割
季节感染人数未感染人数合计感染率（%）
春夏
秋冬合计季节春感染人数 12
12 12
29 35 88 未感染人数 699
699 666
665 717 2747 合计 711
711 678
694 752 2835
1.69 1.77
4.18 4.65 3.10
二、独立样本R×C列联表资料的χ2检验
1. 多个独立样本率的比较（R×2表）
2.多个样本的构成比比较（R×C表）
3.两个样本的构成比比较（2×C表）
R×C表的χ2检验通用公式
基本公式
2
通用公式
2
(A T) A 2 n( 1) T nR nC
2
1.多个独立样本率的比较
( b c 1) 2 , 1 bc
2
（b+c＜40）

第九章 x2检验

医学统计学第九章分类变量资料统计推断第九章χ2检验主要内容:一、四格表资料的χ2检验二、配对四格表资料的χ2检验三、R×C列联表资料的χ2检验第一节率的标准误与总体率的区间估计一、率的抽样误差与标准误在抽样调查中，由抽样造成的样本率与总体率之差，称为率的抽样误差，其大小可用率的标准误描述。

联想：抽样误差和均数的标准误x /x S复习率的标准误的计算公式：(1)p nππσ-=σp 为总体率的标准误，π为总体率，n 为样本含量。

复习(1)p p p S n-=当π未知时，可用样本率p 作为估计值，计算出样本率的标准误S p ，作为σp 估计值.例1为了解某地人群结核菌素试验阳性率情况，某医疗机构在该地人群中随机检测了1773人，结核菌素试验阳性有682人，阳性率为38.47%，试计算其标准误。

%16.10116.017733847.03847.0==)-(1=p s 分析：π未知，用p 来估计，s p 为δp 的估计，p=38.47%,1-p=61.53%二、总体率的区间估计①点估计：π＝p②区间估计：按一定的概率（1－α），以p来估计π所在的范围。

一般α＝0.05或0.01。

1、查表法因其计算比较复杂，统计学家已经编制了总体率可信区间估计用表，可根据样本含量n和阳性数x查阅统计学专著中的附表。

当n较小，如n 50，特别是p接近于0或1时，按二项分布原理估计总体率的可信区间。

例2 某市抽查了20名献血员乙型肝炎表面抗原（HBsAg）携带情况，阳性者4人，求该市献血员HBsAg阳性率的95%可信区间。

分析：n=20,实际发生数x=4，查表得上行：6~44（95%），下行4~51（99%）*如果n=20,实际发生的12（x大于n/2）,如何查？先找n=20,1-x=8,查表得a~b,然后算得（100-b）~(100-a)2、正态近似法条件：n 足够大，p 和(1－p)均不太小，且np≥5和n(1－p)≥5时，p 近似服从正态分布。

心理统计学二第十章χ2检验

一、单因素分类数据的同质性检验二、列联表形式的同质性检验三、计数数据的合并方法
48
一、单因素分类数据的同质性检验
检验步骤： 1. 计算各个样本组的χ 2值和自由度； 2. 累加各样本组χ 2值，计算其总和以及自由度的总和; 3. 将各样本组原始数据按相应类别合并，产生一个总的数据表，并计算这个总数据表的χ2值和自由度； 4. 计算各样本组的累计χ 2值与总测试次数合并获得的χ 2值之差——异质性χ 2值； 5. 查χ 2临界值表，判断χ 2值差是否显著。
14
4、使用校正公式
❖在二乘二的列联表检验中，若单元格的期望次数低于10但高于5，可使用耶茨校正公式来校正。若低于5，或样本总人数低于20，则应使用费舍精确概率检验法。
15
六、应用χ 2检验应注意取样设计
应用χ 2检验时，要十分注意取样的代表性。
16
第二节配合度检验
一、配合度检验的一般问题二、配合度检验的应用三、连续变量分布的吻合性检验
4549505455596064656970747579808485899094959910182240467244281812例例101055一独立性检验的一般问题与步骤一独立性检验的一般问题与步骤二四格表四格表独立性检验独立性检验rcc表独立性检验表独立性检验四多重列联表分析四多重列联表分析一统计假设一统计假设二理论次数的计算二理论次数的计算三自由度的确定三自由度的确定四统计方法的选择四统计方法的选择五结果及解释五结果及解释一独立样本四格表的独立样本四格表的22检验检验二相关样本四格表的相关样本四格表的22检验检验三四格表四格表22值的近似校正值的近似校正四格表的fisherfisher精确概率检验方法精确概率检验方法22独立样本四格表的独立样本四格表的22检验就是双向表检验就是双向表22检验

医学统计学X2检验

2
2
(68 30 22 58) 178 2.00 90 88 126 52
2
3、查X2 界值表确定P值按 V ＝1，查附表5，X2界值表得： X20.05，1 =3.84 X20. 1，1 =2.71 X20.25，1 =1.32 X20.1，1 > X2 > X20.25，1, 0.25 > P>0.1 4、推断结论
63.71
26.29
62.29
25.71
= 2.00
3、查X2 界值表确定P值按 V ＝1，查附表5，X2界值表得： X20.05，1 =3.84 X20. 1，1 =2.71 X20.25，1 =1.32 X20.1，1 > X2 > X20.25，1, 0.25 > P>0.1 4、推断结论
V=1 ，查
x
2
2 界值表得： x0.005 ,1 =7.88，
2 2 x 0.005 ,1 , P<0.005 > x
按α=0.05水准，拒绝H0，接受H1，故可认为甲乙两法的血清学阳性检出率不同，甲法的阳性检出率较高。注意：当a和d的数字特别大而b和c的数字较小时，即使检验结果有统计学意义，而实际意义也不大。故配对四格表 X2检验一般用于检验样本含量不太大的资料。
X2 检验过程
1、建立假设Ｈ0：π1＝π2 Ｈ1：π1≠π2 α＝0.05 2、计算X2值（用基本公式计算） T11＝(90×126)／178＝63.71 T12＝90-63.71＝26.29 T21＝126－63.71＝62.29 T22＝88-62.29＝25.71
2 2 2 2 68 63 . 71 22 26 . 29 58 62 . 29 30 25 . 71 2

卡方检验(第六版)

α’
χ2
P值
A、C两种方案治疗轻、中度高血压的有效率高于B方案，但尚不能认为A、C两种方案的有效率不同。
配对设计资料的χ 第二节配对设计资料的 2检验
一、二分类变量：二分类变量： 1、配对设计、
配对分类资料是把两种处理分别施于条件相似的两个受试对象，或先后施于同一受试对象，逐对记录实验结果。甲、乙两种血清学检查结果有四种： (1)两种方法检查结果均为阳性(a)； (2)两种方法检查结果均为阴性(d)；这是结果相同的部分 (3)甲法阳性乙法阴性(b)； (4)甲法阴性乙法阳性(c)；这是结果不同的部分。如果只考虑结果不同部分有无差别，则作卡方检验。
例11.5 对例11.3 3种方案治疗轻、中度高血压的有效率作进一步的两两比较。多个样本率比较的列联表资料经两两分割，可整理成多个四格表的形式。为保证假设检验时犯I型错误的总的概率不变，必须重新规定每次比较的检验水准为：
α' = 1 − m 1 − α
2 式中 m = C k =
k ( k − 1) 3 × (3 − 1) = =3 2 2
列联表资料的χ 二、配对R×C列联表资料的 2检验：配对 × 列联表资料的某研究欲比较X线和对强直性脊柱炎(AS) 线和CT对强直性脊柱炎 1、例题：例11.7 某研究欲比较线和对强直性脊柱炎、例题：
骶髂关节病变的诊断价值，收集临床上诊断为的患者的患者136 例，对骶髂关节病变的诊断价值，收集临床上诊断为AS的患者 272个骶髂关节分别拍摄线平片和扫描，结果见表个骶髂关节分别拍摄X线平片和扫描，个骶髂关节分别拍摄线平片和CT扫描结果见表11.11。问两。种方法诊断骶髂关节病变的分级有无差别？种方法诊断骶髂关节病变的分级有无差别？表11.11 两种方法诊断骶髂关节病变的分级情况 CT扫描 CT扫描 X线线 0 0 Ⅰ Ⅱ Ⅲ-Ⅳ Ⅳ 合计 17 7 1 0 25 Ⅰ 8 30 6 0 44 Ⅱ 7 28 32 8 75 Ⅲ-Ⅳ Ⅳ 0 14 22 92 128 合计 32 79 61 100 272

统计学x2和p值计算过程

统计学x2和p值计算过程统计学中X^2（卡方）检验和P值的计算过程是用于判断观察值与理论分布是否有显著差异的一种常用统计方法。

本文将详细介绍X^2检验和P值计算的过程。

一、X^2（卡方）检验概述X^2（卡方）检验是一种非参数统计方法，适用于观测数据是分类变量的情况。

它的核心思想是将观测值与理论值进行比较，通过计算卡方值来判断它们之间的差异程度。

计算具体过程如下：1.建立假设：在进行X^2检验时，首先需要建立原假设和备择假设。

原假设（H0）通常为“观测值与理论分布没有显著差异”，备择假设（H1）则通常为“观测值与理论分布存在显著差异”。

2.构建列联表：X^2检验通常使用列联表（Contingency Table）来整理数据，列联表是一个二维表格，行列分别代表两个变量的不同取值，交叉单元中的数值表示对应取值下的观测频数。

3.计算期望值：期望值是指在原假设成立的情况下，理论上每个交叉单元中的期望频数。

计算期望值的公式为：期望频数=（对应行的总频数*对应列的总频数）/总频数。

4.计算卡方值：计算卡方值的公式为：X^2=Σ(观测频数-期望频数)^2/期望频数。

计算得到的卡方值越大，观测值与理论分布之间的差异越大。

5.判断显著性：判断观测值与理论分布之间的差异是否显著，需要结合自由度和显著性水平进行判断。

计算卡方值后，可以查阅卡方分布表，根据初始设定的显著性水平（通常为0.05），确定拒绝域。

6.计算P值：P值是指在原假设成立的情况下，观察到当前或者更极端情况下的概率。

根据卡方分布的性质，可以通过查表或利用统计软件计算出对应的P 值。

如果P值小于设定的显著性水平，就拒绝原假设；否则，不能拒绝原假设。

二、P值计算的方法在进行X^2检验时，计算P值的方法有两种：查表法和计算器法。

下面将分别介绍这两种方法。

1.查表法：查表法是通过查找卡方分布表，确定对应卡方值所对应的P值。

卡方分布表通常提供不同自由度（df，自由度等于行数减1乘以列数减1）和显著性水平下的卡方临界值。

《医学统计学》第九章X的平方检验

22.81
(3 1) (2 1) 2
3. 确定 P 值，作出推断结论
查界值表得 P < 0.05 ，在α=0.05 的检验水准下，拒绝 H0，接受 H1，可以认为三种
疗法的有效率有差别。
医学统计学（第7版）
实例
➢ 例9-6 某研究人员收集了亚洲、欧洲和北美洲，结果见下表，问不同地区人群的血型
1 : 三种治疗方案的总体有效率不全相等
0.05
2. 计算检验统计量，计算 χ2 值：
512
49 2
35 2
45 2
59 2
15 2
254 （

- 1）
100 145 100 109 80 145 80 109 74 145 74 109
2
254 （0.1794 0.2203 0.1056 0.2322 0.3244 0.0279-1）
2
方法。
了解
在小样本情况下的Fisher确切概率法原理及应用，检验的
2
注意事项。
第一节
四格表资料的检验
2
医学统计学（第7版）
一、四格表检验的原理
2
2 检验（chi-square test）：英国统计学家Pearson提出的一
种主要用于分析分类变量数据的假设检验方法，该方
法主要用途是推断两个或多个总体率及构成比之间有
2. 计算检验统计量
6 25 3 24 58 / 2 58

0.376
2

2
c
49 9 28 30
3. 确定 P 值，作出推断结论

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（3）对于有序的R*C表资料不宜用X2检验
（五）、交叉分类2*2表的关联分析
1、 X2检验 2、列联系数r
（六）、2*2配对资料的关联性分析
1、 X2检验注意与配对资料的四格表X2 检验（McNemar检验）不一样，是四格表资料X2检验基本的公式
2、列联系数r
（七总体率（或构成比）
之间有无差别；两种属性的关联性（计
数资料的相关性分析）
• 4、方法：
⑴、专用公式。每一格的T值均＞5且n＞40；
P104，式（7-1）；P105，式（7-4）
⑵、校正公式。有一格的T值＜5且n＞40；
P106，式（7-5）；P106，式（7-6） ⑶、确切概率法。T＜1或n＜40时不计算X2值
（一）列联表资料的X2检验
列联表是按两种属性分类的一种频数数据表。（表内数据为实际频数）分类：交叉分类表
多组分类表
• 交叉分类：是以一个总体抽样后，按两种属性搭配的类确定其个体数目而得。它需检验的是两种属性是否独立（即计数资料的相关性或关联性）
• 多组分类：从多个总体（可视为属性X）分别抽样后，按另一类属性Y的类确定其个体数目而得。它需检验的是各总体按同一属性Y的类的分布概率是否相同。
1、 X2检验 2、列联系数r
(八) 多个样本率比较的X2分割法
1、用途：当多个样本率比较的行*列表X2检验，推论结论为拒绝，接受时，只能认为各总体之间总的来说有差别，需要对每两个总体率之间有无差别作出判断。其分析方法之一就是X2分割法。
2、基本思想：
将2*k表（X2）分割成多个独立的四格表（X2）（其原理是X2分布的可加性），并进行两两比较。要求必须重新规定检验水准，其目的是为保证检验假设中的第一类错误α 的概率不变
3、多个实验组间的两两比较 P114 公式（7-12）
4、实验组与同一对照组的比较 P114 公式（7-13）
（四）、行×列表资料的X2检验
• 1、用途：推断多个总体率（或构成比）之间有无差别；两种属性的关联性（计数资料的相关性分析）
• 2、计算公式： P111，式（7-10） • 3、注意事项：（1）、 X2检验要求理
论频数不能太小，否则将导致分析的偏性。一般认为行×列表中不能有1/5以上格子的理论频数小于5或有一个理论频数小于1。
对理论频数太小有以下三种处理办法：
A、最好增加样本含量，以增加理论频数。 B、删去上述理论频数太小的行或列。 C、将太小理论频数所在的行或列与性质相近的邻行或邻列的实际频数合并。
（2）、当进行多个样本率（或构成比）比较的X2检验，结论为拒绝检验假设H0时，只能认为各总体率（或构成比）之间总的来说有差异，但不能说它们彼此间有差异或某两个间有差别，还需进一步进行两两比较。
• 3、观察结果：四种形式
⑴、甲+乙+ a ； ⑵、甲+乙－ b； ⑶、甲－乙+ c ； ⑷、甲－乙－ d。 • 4、配对资料的专用四格表
• 5、计算公式：McNemar test
⑴、专用公式：b+c＞40 P107，式（7-7）
⑵、校正公式：b+c＜40 P107，式（7-8）
6、注意事项：⑴、要求资料为配对的计数资料；⑵要注意配对资料的四格表X2检验的适用条件
• 关联性检验的假设：H0： ij=I. ×.j H1：H0不成立。
• 多组分类资料分布概率的齐性检验 H0： 1=2=.3 H1：H0不成立
• 共同点：计算的统计量X2及计算公式均一样，自由度也一样为（行—1）×（列—1）
Ｘ２检验（Ｃhi—square test）概述
• 1、基本思想：基本公式（p312，式10-14）中A为实际频数，T为理论频数。它是根据检验假设来确定的。如作两样本率的比较，我们先假设两组的总体率相同，均等于两组合计的总率，再乘上每个样本的样本含量。如果检验假设H0成立，则实际频数A和理论频数T之差一般不会很大，出现大的X2值的概率是很小的；若P＜，我们就怀疑检验假设 H0成，立则的没可有能理性由很拒小绝，它因。而X2拒与绝P值它的；对若应P＞关系 X20可.01查，X2界值表（成反比）。X20.05，；
（Fisher exact probabilities） • 5、注意事项：⑴、要求每个样本要分为互斥的
两类；⑵要注意区分四格表检验的X2公式及其适用条件
（三）、配对资料的四格表X2检验
• 1、用途：对配对资料研究所获得的计数资料进行比较。
• 2、配对设计包含：⑴、同一批样品用两种不同的处理方法；⑵、观察对象根据配对条件配成对子，同一对对子内不同的个体分别接受不同的处理； ⑶、在病因和危险因素的研究中，将病人和对照按配对条件配成对子，研究是否成在某种病因或危险因素
• 2、应用：X2检验就是以X2分布为基础，以X2值为统计量，推断两个或两个以上总体率（或构成比）之间有无差别？变量间有无相关关系？以及检验频数分布的拟和优度。
（二）四格表的X2检验
• 1、特点：2×2列联表；抽两个样本，
每个样本分为互斥的两类结果即可形成
这种资料。
•
2、四格表。
a c