列联表独立性检验

新高考数学复习考点知识讲解列联表与独立性检验1、简单随机抽样得到了X 和Y 的抽样数据列联表2、基于小概率值α的检验规则是：当αχx ≥2时，我们就推断0H 不成立，即认为X 和Y 不独立，该推断犯错误的概率不超过α当αχx <2时，我们没有充分证据推断0H 不成立，可以认为X 和Y 独立这种利用2χ的取值推断分类变量X 和Y 是否独立的方法称为2χ独立性检验，读作“卡方独立性检验”，简称独立性检验3、应用独立性检验解决实际问题大致应包括以下几个主要环节： （1）提出零假设0H ：X 和Y 相互独立，并给出在问题中的解释； （2）根据抽样数据整理出2×2列联表，计算2χ的值，并与临界值αx 比较 （3）根据检验规则得出推断结论（4）在X 和Y 不独立的情况下，根据需要，通过比较相应的频率，分析X 和Y 间的影响规律题型一 变量关系例 1 为了判断两个分类变量X 、Y 是否有关系，应用独立性检验的方法算得2K 的观测值为5，则下列说法中正确的是( ) A ．有95%的把握认为“X 和Y 有关系” B ．有95%的把握认为“X 和Y 没有关系” C ．有99%的把握认为“X 和Y 有关系” D ．有99%的把握认为“X 和Y 没有关系” 【答案】A 【分析】利用2K 的观测值与临界值进行比较得解. 【详解】因为2( 3.841)0.050P K =≥，5 3.841>，所以有95%的把握认为“X 和Y 有关系”. 故选：A若由一个22⨯列联表中的数据计算得2 4.013K =，那么有（ ）把握认为两个变量有关系.知识典例巩固练习()20P K k ≥ 0.500.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.0010k0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828A ．95%B ．97.5%C ．99%D ．99.9%【答案】A 【分析】由2 3.841K >可对照临界值表得到结果. 【详解】2 4.013 3.841K =>，∴有()10.05100%95%-⨯=的把握认为两个变量有关系. 故选：A.题型二 列联表例 2 如表是一个2×2列联表：则表中a ，b 的值分别为（ ）y 1 y 2 合计x 1 a21 73x 2 22 25 47合计 b 46 120A ．94，72B ．52，50C ．52，74D ．74，52【答案】C 【分析】根据表中数据简单计算即可. 【详解】a =73-21=52，b =a +22=52+22=74. 故选：C.下面是一个22⨯列联表:1y 2y总计 1x35 a 70 2x15 1530 总计 50b100其中,a b 处填的值分别为_______． 【答案】35，50. 【分析】由列联表易得结果. 【详解】由3570a +=，得35a =，15a b +=，得50b =.巩固练习故答案为：35，50.题型三 独立性检验应用例 3 2016年3月9日至15日，谷歌人工智能系统“阿尔法”迎战围棋冠军李世石，最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类智慧的胜利，也有许多人持反对意见，有网友为此在某大学进行了调查，参加调查的共80位学生，调查数据的22⨯列联表如下所示: 持反对意见 赟同 总计男40 女 5总计2580（1）①请将列联表补充完整;②请根据表中数据判断，能否有的99.9%把握认为是否持反对意见与性别有关; （2）若表中持反对意见的5个女学生中，3个是大三学生，2个是大四学生.现从这5个学生中随机选2个学生进行进一步调查，求这2个学生是同一年级的概率.附参考公式及数据:()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.()20P K k ≥ 0.40 0.25 0.10 0.010 0.005 0.001 0k7.879 1.3232.7066.6357.87910.828【答案】（1）①列联表见解析，②有99.9%的把握认为是否持反对意见与性别有关；（2）25.【分析】()1①由已知数据得出列联表；②由题可知，计算2K 的观测值013.09110.828k ≈>，可得出结论；()2记3个大三学生分别为，123,,,2A A A 个大四学生分别为12,B B 、运用列举法列出所有事件，由古典概率公式可得答案. 【详解】()1①②由题可知，2K 的观测值2080203552013.09110.828404055(25)k ⨯-⨯=≈>⨯⨯⨯所以有99.9%的把握认为是否持反对意见与性别有关.()2记3个大三学生分别为，123,,,2A A A 个大四学生分别为12,B B 、则从中抽取2个的基本事件有:1213231213112223212,,,,,,,,,A A A A A A AB A B A B A B A B A B B B ，共10个，其中抽取的2人是同一年级的基本事件有12132312,,,A A A A A A B B 共4个， 则这2个学生是同一年级的概率为42105P ==.这一年来人类与新型冠状病毒的“战争”让人们逐渐明白一个道理，人类社会组织模式的差异只是小事情，病毒在地球上存在了三四十亿年，而人类的文明史不过只有几千年而已，人类无法消灭病毒，只能与之共存，或者病毒自然消亡，在病毒面前，个体自由要服从于集体或者群体生命的价值．在传染病学中，通常把从致病刺激物侵入机体内或者对机体发生作用起，到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期，因此我们应该注意做好良好的防护措施和隔离措施．某研究团队统计了某地区10000名患者的相关信息，得到如表表格： 潜伏期（天）(]0,2(]2,4(]4,6(]6,8(]8,10 (]10,12 (]12,14人数6001900300025001600250150（1）新冠肺炎的潜伏期受诸多因素的影响，为研究潜伏期与年龄的关系，通过分层抽样从10000名患者中抽取200人进行研究，完成下面的2×2列联表，并判断能否在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关？潜伏期8≤天潜伏期8>天总计 60岁以上（含60岁）150 60岁以下 30 总计200（2）依据上述数据，将频率作为概率，且每名患者的潜伏期是否超过8天相互独立．为了深入研究，该团队在这一地区抽取了20名患者，其中潜伏期不超过8天的人数最有巩固练习可能是多少？附：()()()()()22n ad bcKa b c d a c b d-=++++．【答案】（1）表格见解析，能；（2）16名.【分析】（1）由表中数据可知，求得潜伏期大于8天的人数，列出2×2列联表，利用公式求得2K的值，结合附表，即可得到结论；（2）求得该地区10000名患者中潜伏期不超过8天的人数，求得潜伏期不超过8天的概率，进而抽取的20名患者中潜伏期不超过8天的人数．【详解】（1）由表中数据可知，潜伏期大于8天的人数为16002501502004010000++⨯=人，补充完整的2×2列联表如下，所以()2220013*********.66710.8281505016040K ⨯⨯-⨯=≈>⨯⨯⨯， 故能在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关．（2）该地区10000名患者中潜伏期不超过8天的人数为6001900300025008000+++=名，将频率视为概率，潜伏期不超过8天的概率为80004100005=， 所以抽取的20名患者中潜伏期不超过8天的人数最有可能是420165⨯=名．1、为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系，运用2×2列联表进行独立性检验，经计算得x 2＝7.01，则认为“喜欢乡村音乐与性别有关系”的把握约为（ ）A ．0.1%B ．1%C ．99%D ．99.9%【答案】C 【分析】由x 2＝7.01>6.635，对照临界值表求解即可.巩固提升【详解】易知x2＝7.01>6.635，对照临界值表知，有99%的把握认为喜欢乡村音乐与性别有关系．故选：C2、某班主任对全班50名学生进行了作业量的评价调查，所得数据如表所示：则认为作业量的大小与学生的性别有关的犯错误的概率不超过（）A．0.01 B．0.05C．0.10 D．无充分证据【答案】B【分析】计算2K，再进行判断.【详解】因为2250(181598)5.059 3.84127232624K⨯⨯-⨯=≈>⨯⨯⨯，又()2 3.8410.05P K≥=所以认为作业量的大小与学生的性别有关的犯错误的概率不超过0.05. 故选：B3、（多选）有关独立性检验的四个命题，其中正确的是（）A．两个变量的2×2列联表中，对角线上数据的乘积相差越大，说明两个变量有关系成立的可能性就越大B．对分类变量X与Y的随机变量2K的观测值k来说，k越小，“X与Y有关系”的可信程度越小C．从独立性检验可知：有95%的把握认为秃顶与患心脏病有关，我们说某人秃顶，那么他有95%的可能患有心脏病D．从独立性检验可知：有99%的把握认为吸烟与患肺癌有关，是指在犯错误的概率不超过1%的前提下认为吸烟与患肺癌有关【答案】ABD【分析】根据独立性检验的原理与知识，对选项中的命题判断正误即可．【详解】选项A，两个变量的2×2列联表中，对角线上数据的乘积相差越大，则2K观测值越大，两个变量有关系的可能性越大，所以选项A正确；选项B，根据2K的观测值k越小，原假设“X与Y没关系”成立的可能性越大，则“X与Y有关系”的可信度越小，所以选项B正确；选项C，从独立性检验可知：有95%的把握认为秃顶与患心脏病有关，不表示某人秃顶他有95%的可能患有心脏病，所以选项C不正确；选项D，从独立性检验可知：有99%的把握认为吸烟与患肺癌有关，是指在犯错误的概率不超过1%的前提下认为吸烟与患肺癌有关，是独立性检验的解释，所以选项D正确.故选：ABD.4、为了判断某高中学生是否选修文科与性别的关系，现随机抽取50名学生，得到如下2×2列联表：已知P (x 2≥3.841)≈0.05，P (x 2≥6.635)≈0.01.根据表中数据，得到x 2＝250(1320107)23272030⨯⨯-⨯⨯⨯⨯≈4.844，则认为选修文科与性别有关系出错的概率约为________．【答案】0.05 【分析】直接根据表中数据计算的x 2值与P (x 2≥3.841)≈0.05比较判断，即得结果. 【详解】因为x 2≈4.844>3.841，而P (x 2≥3.841)≈0.05，故认为选修文科与性别有关系出错的概率约为0.05. 故答案为：0.05.5、调查者通过询问72名男、女大学生在购买食品时是否看营养说明得到的数据如下表所示:大学生的性别和是否看营养说明之间___(填“有”或“没有”)关系.【答案】有【分析】由表中的数据直接计算卡方，从而可得结论【详解】解：因为22722820168)=8.4167.879 44283636χ⨯⨯-⨯≈>⨯⨯⨯（，所以有的把握认为大学生性别与购买食品时是否看营养说明之间有关，故答案为：有6、某高校《统计》课程的教师随机调查了选该课的一些学生情况，具体数据如下表: 为了判断主修统计专业是否与性别有关系，根据表中的数据，得到k=2 50(1320-107) 23272030⨯⨯⨯⨯⨯⨯＝4.844>3.841，所以有_____的把握判定主修统计专业与性别有关系.附：【答案】95%【分析】根据独立性检验的基本思想，因为2K的观测值k＝4.844>3.841，参考临界值表即可得出【详解】根据表格数据得2K的观测值k=250(1320-107)23272030⨯⨯⨯⨯⨯⨯≈4.844 3.841>，所以有95%的把握判定主修统计专业与性别有关系.故答案为:95%．7、某学生对其30名亲属的饮食习惯进行了一次调查，依据统计所得数据可得到如下的22⨯列联表：根据以上列联表中的数据，可得2K 的观测值k =__________，__________（填“有”或“没有”）99%的把握认为其亲属的饮食习惯与年龄有关．参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++．参考数据：【答案】10 有 【分析】根据列联表，求得a b c d ,,,的值，利用公式，求得2K 的值，结合附表，即可得到结论. 【详解】由列联表可得20a =，10b =，12c =，4d =，可得2230(8128)10 6.63512182010K ⨯-==>⨯⨯⨯， 所以有99%的把握认为其亲属的饮食习惯与年龄有关． 故答案为：10；有.8、2017年3月27日，一则“清华大学要求从2017级学生开始，游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响．游泳作为一项重要的求生技能和运动项目受到很多人的喜爱．其实，已有不少高校将游泳列为必修内容．某中学为了解2018届高三学生的性别和喜爱游泳是否有关，对100名高三学生进行了问卷调查，得到如下列联表：已知在这100人中随机抽取1人，抽到喜欢游泳的学生的概率为35.（1）请将上述列联表补充完整；（2）判断是否有99.9%的把握认为喜欢游泳与性别有关．附：x2＝2()()()()()n ad bca b c d a c b d-++++【答案】（1）表格见解析；（2）有. 【分析】（1）根据概率补全列联表即可；（2）计算2x，再进行判断即可.【详解】（1）因为在100人中随机抽取1人抽到喜欢游泳的学生的概率为3 5所以喜欢游泳的学生人数为3 100605⨯=.其中女生有20人，男生有40人，列联表补充如下：（2）因为22100(40302010)16.6710.82860405050x⨯⨯-⨯=≈>⨯⨯⨯所以有99.9%的把握认为喜欢游泳与性别有关．9、某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查，得出以下22⨯列联表：如果随机抽查该班的一名学生，那么抽到积极参加班级工作的学生的概率是12 25．（1）求a，b，c，d的值．（2）试运用独立性检验的思想方法分析：能否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系？并说明理由．参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++．参考数据：【答案】（1）6a =，19b =，24c =，26d =；（2）有. 【分析】（1）由抽到积极参加班级工作的学生的概率是1225，可求出c 的值，然后根据表中的数据可求出,,a b d 的值；（2）直接利用22()()()()()n ad bc K a b c d a c b d -=++++公式求解，然后根临界值表判断即可【详解】解：（1）积极参加班级工作的学生有c 人，总人数为50， 由抽到积极参加班级工作的学生的概率1125025c P ==， 解得24c =，所以6a =．所以2525619b a =-=-=，50502426d c =-=-=．（2）由列联表知，2250(181967)11.53825252426K ⨯⨯-⨯=≈⨯⨯⨯， 由11.53810.828>，可得有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系．。

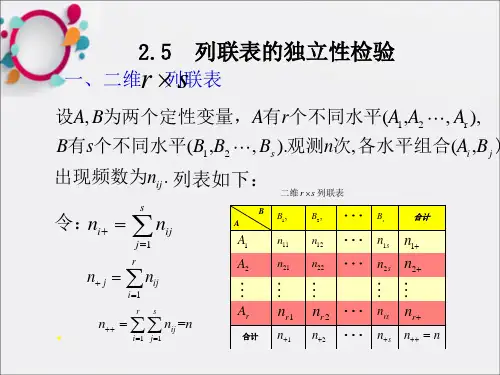
第2课时列联表与独立性检验课标解读考向预测1.通过实例，理解2×2列联表的统计意义.2.通过实例，了解2×2列联表独立性检验及其应用.预计2025年高考列联表、独立性检验可能会以实际问题为背景，与概率、随机变量的分布列及数字特征相结合命题，难度适中.必备知识——强基础1．分类变量：变量的不同“值”表示个体所属的不同类别，像这样的变量称为分类变量．2．2×2列联表一般地，假设有两个分类变量X和Y，它们的取值均为0，1，其2×2列联表为XY合计Y＝0Y＝1X＝0a b a＋bX＝1c d c＋d合计a＋c b＋d a＋b＋c＋d3．独立性检验(1)零假设：以Ω为样本空间的古典概型，设X和Y为定义在Ω上，取值于{0，1}的成对分类变量，H0：01P(Y＝1|X＝0)＝P(Y＝1|X＝1)．通常称H0为零假设或原假设．(2)χ2的计算公式：记n＝a＋b＋c＋d，则χ2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d）.(3)临界值：对于任何小概率值α，可以找到相应的正实数xα，使得后面关系成立：P(χ2≥xα)＝α.我们称xα为α的临界值，这个临界值就可以作为判断χ2大小的标准，概率值α02越小，临界值xα越大．(4)基于小概率值α的检验规则是：当χ2≥xα时，我们就推断H0不成立，即认为X和Y不独立，该推断犯错误的概率不超过α；当χ2＜xα时，我们没有充分证据推断H0不成立，可以认为X和Y独立．(5)应用独立性检验解决实际问题的主要环节①提出零假设H0：X和Y相互独立，并给出在问题中的解释；②根据抽样数据整理出2×2列联表，计算χ2的值，并与临界值xα比较；③根据检验规则得出推断结论；④在X和Y不独立的情况下，根据需要，通过比较相应的频率，分析X和Y间的影响规律．根据χ2的值可以判断两个分类变量有关的可信程度，若χ2越大，则认为两分类变量有关的把握越大．1．概念辨析(正确的打“√”，错误的打“×”)(1)分类变量中的变量与函数中的变量是同一概念．()(2)2×2列联表是借助两个分类变量之间频率大小差异说明两个变量之间是否有关联．()(3)应用独立性检验的基本思想对两个变量间的关系作出的推断一定是正确的．()(4)若分类变量X，Y关系越密切，则由观测数据计算得到的χ2的观测值越小．()答案(1)×(2)√(3)×(4)×2．小题热身(1)(人教B选择性必修第二册4.3.2练习A T2改编)为了解某大学的学生是否爱好体育锻炼，用简单随机抽样方法在校园内调查了120位学生，得到如下2×2列联表：男女合计爱好a b73不爱好c25合计74则a－b－c＝()A．7B．8C．9D．10答案C解析根据题意，可得c ＝120－73－25＝22，a ＝74－22＝52，b ＝73－52＝21，∴a －b －c＝52－21－22＝9.(2)在下列两个分类变量X ，Y 的样本频数列联表中，可以判断X ，Y 之间有无关系的是()y 1y 2合计x 1a b a ＋b x 2c d c ＋d 合计a ＋cb ＋da ＋b ＋c ＋dA ．|a a ＋b －b c ＋d |B ．|c a ＋b －d c ＋d|C ．|b a ＋b －c c ＋d |D ．|a a ＋b －c c ＋d |答案D解析∵χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ），则分类变量X 和Y 有关系时，ad 与bc 差距会比较大，由a a ＋b －c c ＋d ＝ac ＋ad －ac －bc （a ＋b ）（c ＋d ）＝ad －bc （a ＋b ）（c ＋d ），故a a ＋b 与cc ＋d 的值相差应该大，即|a a ＋b －c c ＋d |的大小可以判断X ，Y 之间有无关系．(3)已知P (χ2≥6.635)＝0.01，P (χ2≥10.828)＝0.001.在检验喜欢某项体育运动与性别是否有关的过程中，某研究员搜集数据并计算得到χ2＝7.235，则根据小概率值α＝________的χ2独立性检验，分析喜欢该项体育运动与性别有关．答案0.01解析因为6.635<7.235<10.828，所以根据小概率值α＝0.01的χ2独立性检验，分析喜欢该项体育运动与性别有关．考点探究——提素养考点一分类变量的两种统计表示形式(多考向探究)考向1等高堆积条形图例1(2023·四川南充三诊)为考查A ，B 两种药物预防某疾病的效果，进行动物实验，分别得到如下等高堆积条形图，根据图中信息，下列说法最佳的是()A ．药物B 的预防效果优于药物A 的预防效果B ．药物A 的预防效果优于药物B 的预防效果C ．药物A ，B 对该疾病均有显著的预防效果D ．药物A ，B 对该疾病均没有预防效果答案B解析根据题干中两个等高堆积条形图知，药物A 实验显示不服药与服药时患病差异较药物B 实验显示明显，所以药物A 的预防效果优于药物B 的预防效果．【通性通法】在等高堆积条形图中，a a ＋b 与cc ＋d 相差越大，我们认为两个分类变量之间关系越强．【巩固迁移】1．(多选)现行普通高中学生在高一时面临着选科的问题，学校抽取了部分男、女学生意愿的一份样本，制作出如下两个等高堆积条形图：根据这两幅图中的信息，下列统计结论正确的是()A ．样本中的女生数量多于男生数量B ．样本中有两理一文意愿的学生数量多于有两文一理意愿的学生数量C ．样本中的男生偏爱两理一文D ．样本中的女生偏爱两文一理答案ABC解析由等高堆积条形图知，女生数量多于男生数量，故A 正确；有两理一文意愿的学生数量多于有两文一理意愿的学生数量，故B 正确；男生偏爱两理一文，故C 正确；女生中有两理一文意愿的学生数量多于有两文一理意愿的学生数量，故D 错误．故选ABC.考向22×2列联表例2(1)下面是一个2×2列联表，则表中a ，c 处的值分别为()X Y 合计y 1y 2x 1a 2573x 221b c合计d 49A ．98，28B ．28，98C ．48，45D ．45，48答案C解析由2×2列联表知a ＋25＝73，b ＋25＝49，b ＋21＝c ，解得a ＝48，b ＝24，c ＝45.故选C.(2)假设两个分类变量X 和Y 的2×2列联表如下：X Y 合计y 1y 2x 1a 10a ＋10x 2c 30c ＋30合计a ＋c40100对于同一样本，以下数据能说明X 和Y 有关系的可能性最大的一组是()A ．a ＝40，c ＝20B ．a ＝45，c ＝15C ．a ＝35，c ＝25D ．a ＝30，c ＝30答案B解析χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）＝根据2×2列联表和独立性检验的相关知识，知当b ，d 一定时，a ，c 相差越大，a a ＋10与cc ＋30相差就越大，χ2就越大，即X和Y有关系的可能性越大，结合选项，知B中a－c＝30与其他选项相比相差最大．【通性通法】在2×2列联表中，如果两个变量没有关系，则应满足ad－bc≈0.|ad－bc|越小，说明两个变量之间关系越弱；|ad－bc|越大，说明两个变量之间关系越强．【巩固迁移】2．(多选)有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀，得到列联表如下：班级数学成绩优秀非优秀合计甲班10b乙班c30合计105已知在全部105人中随机抽取1人，成绩优秀的概率为27，则下列说法正确的是()A．c＝30，b＝35B．c＝15，b＝50C．c＝20，b＝45D．由列联表可看出数学成绩与班级有关系答案CD解析依题意10＋c105＝27，解得c＝20，由10＋20＋b＋30＝105，解得b＝45.补全2×2列联表如下：班级数学成绩合计优秀非优秀甲班104555乙班203050合计3075105甲班学生数学成绩的优秀率为1055≈0.182，乙班学生数学成绩的优秀率为2050＝0.4，乙班学生数学成绩的优秀率明显高于甲班学生数学成绩的优秀率，可以认为两班学生的数学成绩优秀率存在差异，所以数学成绩与班级有关．故选CD.考点二独立性检验的应用例3(2024·山西太原模拟)为进一步保护环境，加强治理空气污染，某市环保监测部门对市区空气质量进行调研，随机抽查了市区100天的空气质量等级与当天空气中SO2的浓度(单位：μg/m3)，整理数据得到下表：SO2的浓度空气质量等级[0，50](50，150](150，475]1(优)28622(良)5783(轻度污染)3894(中度污染)11211若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”，根据上述数据，回答以下问题：(1)估计事件“该市一天的空气质量好，且SO2的浓度不超过150”的概率；(2)完成下面的2×2列联表；SO2的浓度空气质量[0，150](150，475]合计空气质量好空气质量不好合计(3)根据(2)中的列联表，依据小概率值α＝0.01的独立性检验，能否据此推断该市一天的空气质量与当天SO2的浓度有关？解(1)由表格可知，该市一天的空气质量好，且SO2的浓度不超过150的天数为28＋6＋5＋7＝46，则“该市一天的空气质量好，且SO2的浓度不超过150”的概率P＝46100＝0.46.(2)由表格数据可得列联表如下，SO2的浓度空气质量[0，150](150，475]合计空气质量好461056空气质量不好242044合计7030100(3)零假设为H 0：该市一天的空气质量与当天SO 2的浓度无关．由(2)知χ2＝100×（46×20－10×24）256×44×70×30≈8.936>6.635＝x 0.01，根据小概率值α＝0.01的独立性检验，我们推断H 0不成立，即认为该市一天的空气质量与当天SO 2的浓度有关，此推断犯错误的概率不超过0.01.【通性通法】独立性检验的一般步骤(1)根据样本数据制成2×2列联表；(2)根据公式χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）计算；(3)比较χ2与临界值的大小关系，作统计推断．【巩固迁移】3．(2022·全国甲卷)甲、乙两城之间的长途客车均由A 和B 两家公司运营，为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城之间的500个班次，得到下面列联表：准点班次数未准点班次数A 24020B21030(1)根据上表，分别估计这两家公司甲、乙两城之间的长途客车准点的概率；(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关？附：χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ），α0.1000.0500.010x α2.7063.8416.635解(1)根据表中数据，A 家公司共有班次260次，其中准点班次有240次，设A 家公司长途客车准点事件为M ，则P (M )＝240260＝1213；B 家公司共有班次240次，其中准点班次有210次，设B 家公司长途客车准点事件为N ，则P (N )＝210240＝78.故A 家公司长途客车准点的概率为1213，B 家公司长途客车准点的概率为78.(2)由题可得χ2＝500×（240×30－20×210）2（240＋20）×（210＋30）×（240＋210）×（20＋30）≈3.205＞2.706，根据临界值表可知，有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关．课时作业一、单项选择题1．如表是2×2列联表，则表中a ，b 的值分别为()y 1y 2合计x 1a 835x 2113445合计b4280A ．27，38B ．28，38C ．27，37D ．28，37答案A解析a ＝35－8＝27，b ＝a ＋11＝27＋11＝38.2．某课外兴趣小组通过随机调查，利用2×2列联表和χ2统计量研究数学成绩优秀是否与性别有关．计算得χ2＝6.748，经查阅临界值表知P (χ2≥6.635)＝0.010，则下列判断正确的是()A ．每100名数学成绩优秀的人中就会有1名是女生B ．若某人数学成绩优秀，那么他为男生的概率是0.010C ．有99%的把握认为“数学成绩优秀与性别无关”D ．在犯错误的概率不超过1%的前提下认为“数学成绩优秀与性别有关”答案D解析∵χ2＝6.748>6.635，∴有99%的把握认为“数学成绩优秀与性别有关”，即在犯错误的概率不超过1%的前提下认为“数学成绩优秀与性别有关”．故选D.3．假设有两个分类变量X与Y，它们的可能取值分别为{x1，x2}和{y1，y2}，其2×2列联表为y1y2合计x1101828x2m26m＋26合计m＋1044m＋54则当整数m取________时，X与Y的关系最弱．()A．8B．9C．14D．19答案C解析在两个分类变量的列联表中，当|ad－bc|的值越小时，认为两个分类变量有关的可能性越小．令|ad－bc|＝0，得10×26＝18m，解得m≈14.4，又m为整数，所以当m＝14时，X与Y的关系最弱．4．(2024·海南华侨中学模拟)某同学寒假期间对其30位亲属的饮食习惯进行了一次调查，列出了如下2×2列联表：偏爱蔬菜偏爱肉类合计50岁以下481250岁以上16218合计201030则可以说其亲属的饮食习惯与年龄有关的把握为()附：χ2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d），其中n＝a＋b＋c＋d.α0.0500.0100.001xα 3.841 6.63510.828A．90%B．95% C．99%D．99.9%答案C解析根据列联表中数据，计算χ2＝30×（4×2－8×16）212×18×20×10＝10＞6.635，可以说其亲属的饮食习惯与年龄有关的把握为99%.故选C.5．为了考查某种病毒疫苗的效果，现随机抽取100只小白鼠进行试验，得到如下2×2列联表：感染未感染合计服用104050未服用203050合计3070100附：χ2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d），其中n＝a＋b＋c＋d.α0.100.050.0250.0100.0050.001xα 2.706 3.841 5.024 6.6357.87910.828根据以上数据，得到的结论正确的是()A．在犯错误的概率不超过2.5%的前提下，认为“小白鼠是否被感染与有没有服用疫苗有关”B．在犯错误的概率不超过1%的前提下，认为“小白鼠是否被感染与有没有服用疫苗有关”C．有95%的把握认为“小白鼠是否被感染与有没有服用疫苗有关”D．有95%的把握认为“小白鼠是否被感染与有没有服用疫苗无关”答案C解析依题意，χ2＝100×（10×30－40×20）250×50×30×70＝10021≈4.762，显然有3.841<4.762<5.024<6.635，所以有95%的把握认为“小白鼠是否被感染与有没有服用疫苗有关”，A，B，D不正确，C正确．6．假设有两个变量x与y的2×2列联表如下：y1y2x1a bx2c d对于以下数据，对同一样本能说明x与y有关系的可能性最大的一组为()A．a＝20，b＝30，c＝40，d＝50B．a＝50，b＝30，c＝30，d＝40C．a＝30，b＝60，c＝20，d＝50D．a＝50，b＝30，c＝40，d＝30答案B解析对于A，|ad－bc|＝200；对于B，|ad－bc|＝1100；对于C，|ad－bc|＝300；对于D，|ad －bc|＝300，显然B中|ad－bc|最大，该组数据能说明x与y有关系的可能性最大．7．为了解某社区60岁以上老年人使用手机支付和现金支付的情况，抽取了部分居民作为样本，统计其喜欢的支付方式，并制作出如下等高堆积条形图：根据图中的信息，下列结论中不正确的是()A．样本中多数男性喜欢手机支付B．样本中的女性数量少于男性数量C．样本中多数女性喜欢现金支付D．样本中喜欢现金支付的数量少于喜欢手机支付的数量答案C解析对于A，由题中右图可知，样本中多数男性喜欢手机支付，A正确；对于B，由题中左图可知，样本中的男性数量多于女性数量，B正确；对于C，由题中右图可知，样本中多数女性喜欢手机支付，C不正确；对于D，由题中右图可知，样本中喜欢现金支付的数量少于喜欢手机支付的数量，D正确．故选C.8．针对短视频热，某高校团委对学生性别和喜欢短视频是否有关联进行了一次调查，其中被调查的男生、女生人数均为5m(m∈N*)，男生中喜欢短视频的人数占男生人数的45，女生中喜欢短视频的人数占女生人数的35.零假设为H0：喜欢短视频和性别相互独立．若依据α＝0.05的独立性检验认为喜欢短视频和性别不独立，则m的最小值为()附：χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）.α0.050.01x α3.8416.635A ．7B ．8C ．9D ．10答案C解析根据题意，不妨设a ＝4m ，b ＝m ，c ＝3m ，d ＝2m ，于是χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）＝10m ·（5m 2）25m ·5m ·7m ·3m ＝10m21，由于依据α＝0.05的独立性检验认为喜欢短视频和性别不独立，根据表格可知10m 21≥3.841，解得m ≥8.0661，于是m 的最小值为9.二、多项选择题9．(2024·福建福州一中模拟)“一粥一饭，当思来之不易”，道理虽简单，但每年我国还是有2000多亿元的餐桌浪费，被倒掉的食物相当于2亿多人一年的口粮．为营造“节约光荣，浪费可耻”的氛围，某市发起了“光盘行动”．某机构为调研民众对“光盘行动”的认可情况，在某大型餐厅中随机调查了90位来店就餐的客人，制成如下所示的列联表，通过计算得到χ2的观测值为9.认可不认可40岁以下202040岁以上(含40岁)4010已知P (χ2≥6.635)＝0.010，P (χ2≥10.828)＝0.001，则下列判断正确的是()A ．在该餐厅用餐的客人中大约有66.7%的客人认可“光盘行动”B ．在该餐厅用餐的客人中大约有99%的客人认可“光盘行动”C ．有99%的把握认为对“光盘行动”的认可情况与年龄有关D ．在犯错误的概率不超过0.001的前提下，认为对“光盘行动”的认可情况与年龄有关答案AC解析∵χ2的观测值为9，且P (χ2≥6.635)＝0.010，P (χ2≥10.828)＝0.001，又9＞6.635，但9＜10.828，∴有99%的把握认为对“光盘行动”的认可情况与年龄有关，或者说，在犯错误的概率不超过0.010的前提下，认为对“光盘行动”的认可情况与年龄有关，故C正确，D错误；由表可知，认可“光盘行动”的人数为60，∴在该餐厅用餐的客人中认可“光盘行动”的比例为60×100%≈66.7%，故A正确，B错误．故选AC.9010．为了解阅读量多少与幸福感强弱之间的关系，一个调查机构根据所得到的数据，绘制了如下所示的2×2列联表(个别数据暂用字母表示)：幸福感强幸福感弱合计阅读量多m1872阅读量少36n78合计9060150计算得χ2≈12.981，参照下表：α0.100.050.0250.0100.0050.001xα 2.706 3.841 5.024 6.6357.87910.828下列说法正确的是()A．根据小概率值α＝0.010的独立性检验，可以认为“阅读量多少与幸福感强弱无关”B．m＝54C．根据小概率值α＝0.005的独立性检验，可以在犯错误的概率不超过0.5%的前提下认为“阅读量多少与幸福感强弱有关”D．n＝52答案BC解析∵χ2≈12.981>7.879>6.635，∴根据小概率值α＝0.010的独立性检验，可以在犯错误的概率不超过1%的前提下认为“阅读量多少与幸福感强弱有关”，根据小概率值α＝0.005的独立性检验，可以在犯错误的概率不超过0.5%的前提下认为“阅读量多少与幸福感强弱有关”，∴A错误，C正确；∵m＋36＝90，18＋n＝60，∴m＝54，n＝42，∴B正确，D错误．故选BC.三、填空题11．某校为研究该校学生性别与体育锻炼的经常性之间的联系，随机抽取100名学生(其中男生60名，女生40名)，并绘制得到如图所示的等高堆积条形图，则这100名学生中经常锻炼的人数为________．答案68解析这100名学生中经常锻炼的人数为60×0.8＋40×0.5＝68.12．长绒棉是世界上纤维品质最优的棉花，也是全球高端纺织品及特种纺织品的重要原料．新疆具有独特的自然资源优势，是我国最大的长绒棉生产基地，产量占全国长绒棉总产量的95%以上．新疆某农科所为了研究不同土壤环境下棉花的品质，选取甲、乙两地实验田进行种植．在棉花成熟后采摘，分别从甲、乙两地采摘的棉花中各随机抽取50份样本，测定其马克隆值，整理测量数据得到如下2×2列联表(单位：份)，其中40≤a≤50且a∈N*.注：棉花的马克隆值是反映棉花纤维细度与成熟度的综合指标，是棉纤维重要的内在质量指标之一．根据现行国家标准规定，马克隆值可分为A，B，C三个级别，A级品质最好，B级为标准级，C级品质最差．A级或B级C级合计甲地a50－a50乙地80－a a－3050合计8020100当a＝a0时，有99%的把握认为该品种棉花的马克隆值级别与土壤环境有关，则a0的最小值为________．附：χ2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d），其中n＝a＋b＋c＋d.α0.0500.0100.001xα 3.841 6.63510.828答案46解析依题意，χ2≥6.635，即100×[a（a－30）－（50－a）（80－a）]250×50×80×20≥6.635，(10a－400)2≥2654，由于40≤a≤50且a∈N*，所以10a－400≥2654，a≥40＋265410，因为45<40＋265410<46，所以a0的最小值为46.四、解答题13．某城市地铁将于2024年6月开始运营，为此召开了一个价格听证会，拟定价格后又进行了一次调查，随机抽查了50人，他们的收入与态度如下：月收入(单位：百元)[15，25)[25，35)[35，45)赞成定价者人数123认为价格偏高者人数4812月收入(单位：百元)[45，55)[55，65)[65，75]赞成定价者人数534认为价格偏高者人数521(1)若以区间的中点值作为该区间内的人均月收入，求参与调查的人员中“赞成定价者”与“认为价格偏高者”的月平均收入的差距(结果保留两位小数)；(2)由以上统计数据列出2×2列联表，依据小概率值α＝0.01的独立性检验，可否认为“月收入以55百元为分界点对地铁定价的态度有差异”？附：χ2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d），其中n＝a＋b＋c＋d.α0.10.050.010.005xα 2.706 3.841 6.6357.879解(1)“赞成定价者”的月平均收入为x1＝20×1＋30×2＋40×3＋50×5＋60×3＋70×41＋2＋3＋5＋3＋4≈50.56.“认为价格偏高者”的月平均收入为x2＝20×4＋30×8＋40×12＋50×5＋60×2＋70×14＋8＋12＋5＋2＋1＝38.75，∴“赞成定价者”与“认为价格偏高者”的月平均收入的差距是x1－x2≈50.56－38.75＝11.81(百元)．(2)根据条件可得2×2列联表如下：对地铁定价的态度月收入合计不低于55百元的人数低于55百元的人数认为价格偏高者32932赞成定价者71118合计104050零假设为H0：月收入以55百元为分界点对地铁定价的态度无差异．χ2＝50×（3×11－29×7）232×18×10×40≈6.27＜6.635＝x0.01，∴根据小概率值α＝0.01的独立性检验，没有充分证据推断H0不成立，因此可以认为“月收入以55百元为分界点对地铁定价的态度无差异”．14．(2023·全国甲卷)一项试验旨在研究臭氧效应，试验方案如下：选40只小白鼠，随机地将其中20只分配到试验组，另外20只分配到对照组，试验组的小白鼠饲养在高浓度臭氧环境，对照组的小白鼠饲养在正常环境，一段时间后统计每只小白鼠体重的增加量(单位：g)．试验结果如下：对照组的小白鼠体重的增加量从小到大排序为15.218.820.221.322.523.225.826.527.530.132.634.334.835.635.635.836.237.340.543.2试验组的小白鼠体重的增加量从小到大排序为7.89.211.412.413.215.516.518.018.819.219.820.221.622.823.623.925.128.232.336.5(1)计算试验组的样本平均数；(2)(ⅰ)求40只小白鼠体重的增加量的中位数m，再分别统计两样本中小于m与不小于m的数据的个数，完成如下列联表；＜m≥m对照组试验组(ⅱ)根据(ⅰ)中的列联表，能否有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异？附：χ2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d），α0.1000.0500.010xα 2.706 3.841 6.635解(1)试验组的样本平均数为120×(7.8＋9.2＋11.4＋12.4＋13.2＋15.5＋16.5＋18.0＋18.8＋19.2＋19.8＋20.2＋21.6＋22.8＋23.6＋23.9＋25.1＋28.2＋32.3＋36.5)＝39620＝19.8.(2)(ⅰ)依题意，可知这40只小白鼠体重的增加量的中位数是将两组数据合在一起，从小到大排序后第20位与第21位数据的平均数，第20位数据为23.2，第21位数据为23.6，所以m＝23.2＋23.62＝23.4，故列联表为＜m≥m对照组614试验组146(ⅱ)由(ⅰ)可得，χ2＝40×（6×6－14×14）220×20×20×20＝6.4＞3.841，所以能有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异．。