刚体转动惯量的测定

1mm 实验2 扭摆法测定物体的转动惯量【实验目的】1.熟悉转动惯量测试仪的使用方法。

2.掌握测试仪常数（弹簧的扭转常数）K 的测定。

3.用扭摆法测定几种不同形状物体的转动惯量，并与理论值进行比较。

【实验仪器】转动惯量测试仪，空心金属圆柱体、实心塑料圆柱体、塑料圆球、细金属杆。

【实验原理】将物体在水平面内转过一角度θ后，在弹簧的恢复力矩作用下物体就开始绕垂直轴作往返扭转运动。

根据虎克定律，弹簧受扭转而产生的恢复力矩M 与所转过的角度θ成正比，即M ＝－K θ （2-1） 式中，K 为弹簧的扭转常数，根据转动定律 M ＝I β式中，I 为物体绕转轴的转动惯量，β为角加速度，由上式得 IM ＝β （2-2）令 LK=2ω 忽略轴承的磨擦阻力矩，由（2-1）、（2-2）得 θωθθβ222-=-==IKdt d 上述方程表示扭摆运动具有角简谐振动的特性，角加速度与角位移成正比，且方向相反。

此方程的解为：2θ＝Acos(ωt ＋φ)式中，A 为谐振动的角振幅，φ为初相位角，ω为角速度，此谐振动的周期为 KIT πωπ22==（2-3） 由（2-3）可知，只要实验测得物体扭摆的摆动周期，并在I 和K 中任何一个量已知时即可计算出另一个量。

本实验用一个几何形状规则的物体，它的转动惯量可以根据它的质量和几何尺寸用理论公式直接计算得到，再算出本仪器弹簧的K 值。

若要测定其它形状物体的转动惯量，只需将待测物体安放在本仪器顶部的各种夹具上，测定其摆动周期，由公式（2-3）即可算出该物体绕转动轴的转动惯量。

理论分析证明，若质量为m 的物体绕通过质心轴的转动惯量为I O 时，当转轴平行移动距离X 时，则此物体对新轴线的转动惯量变为I O ＋mx 2。

称为转动惯量的平行轴定理。

【实验内容】1. 测定弹簧的扭转常数，调整测试仪座底脚螺丝，使水平仪的气泡位于中心。

由于弹簧的扭转常数K 值不是固定常数，它与摆动角度略有关系，摆角在90º左右基本相同，在小角度时变小。

实验三刚体转动惯量的测定转动惯量是刚体转动中惯性大小的量度。

它与刚体的质量、形状大小和转轴的位置有关。

形状简单的刚体，可以通过数学计算求得其绕定轴的转动惯量；而形状复杂的刚体的转动惯量，则大都采用实验方法测定。

下面介绍一种用刚体转动实验仪测定刚体的转动惯量的方法。

实验目的：1、理解并掌握根据转动定律测转动惯量的方法；2、熟悉电子毫秒计的使用。

实验仪器：刚体转动惯量实验仪、通用电脑式毫秒计。

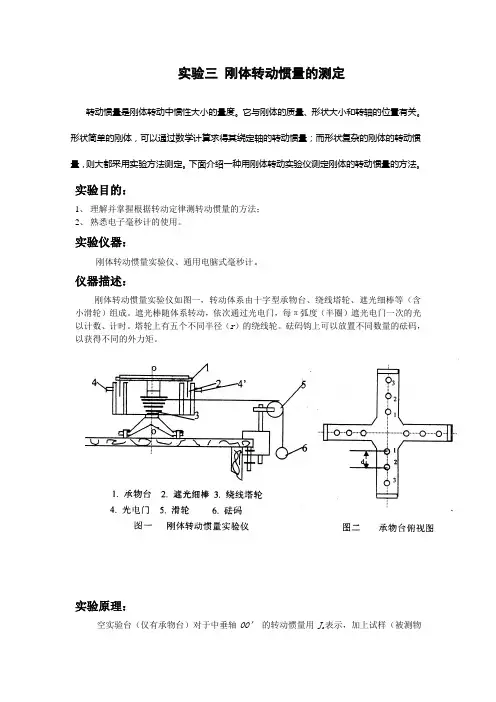
仪器描述：刚体转动惯量实验仪如图一，转动体系由十字型承物台、绕线塔轮、遮光细棒等（含小滑轮）组成。

遮光棒随体系转动，依次通过光电门，每π弧度（半圈）遮光电门一次的光以计数、计时。

塔轮上有五个不同半径（r）的绕线轮。

砝码钩上可以放置不同数量的砝码，以获得不同的外力矩。

实验原理：空实验台（仅有承物台）对于中垂轴OO’的转动惯量用J o表示，加上试样（被测物体）后的总转动惯量用J 表示，则试样的转动惯量J 1 ：J 1 = J –J o (1) 由刚体的转动定律可知：T r – M r = J α (2) 其中M r 为摩擦力矩。

而 T = m(g -r α) (3) 其中 m —— 砝码质量 g —— 重力加速度 α —— 角加速度 T —— 张力1． 测量承物台的转动惯量J o未加试件，未加外力（m=0 , T=0）令其转动后，在M r 的作用下，体系将作匀减速转动，α=α1，有 -M r1 = J o α1 (4) 加外力后，令α =α2m(g –r α2)r –M r1 = J o α2 (5) （4）（5）式联立得J o =212212mr mgrααααα--- (6)测出α1 , α2，由（6）式即可得J o 。

2． 测量承物台放上试样后的总转动惯量J ，原理与1.相似。

加试样后，有 -M r2=J α3 (7) m(g –r α4)r –Mr 2= J α4 (8)∴ J =234434mr mgr ααααα--- (9)注意：α1 , α3值实为负，因此（6）、（9）式中的分母实为相加。

刚体转动惯量的测定【实验目的】1． 测定刚体的转动惯量。

2． 验证转动定律及平行移轴定理。

【实验仪器】1．JM-3 智能转动惯量实验仪。

2． 电脑毫秒计。

【实验原理】转动惯量是反映刚体转动惯性大小的物理量，它与刚体的质量及质量对轴的分布有关。

对于几何形状规则，质量分布均匀的物体，可以计算出转动惯量。

但对于几何形状不规则的物体，以及质量分布不均匀的物体，只能用实验方法来测量。

本实验是用转动惯量实验仪和通用电脑式毫秒计来测量几种刚体的转动惯量，并与计算结果加以比较。

转动惯量实验仪，是一架绕竖直轴转动的圆盘支架。

如图一和图二所示。

待测物体可以放 5 6 1. 承物台 2. 遮光细棒 3. 绕线塔轮4. 光电门5. 滑轮6. 砝码图一 刚体转动惯量实验仪 图二 承物台俯视图设转动惯量仪空载（不加任何试件）时的转动惯量为J 0。

我们称它为该系统的本底转动惯量，加试件后该系统的转动惯量用J 1表示，根据转动惯量的叠加原理，该试件的转动惯量J 2为：J 2=J 1－J 0 （1）如何测量J 0、J 1让我们从刚体动力学的理论来加以推导。

一、如果不给该系统加外力矩（即不加重力砝码），该系统在某一个初角速度的启动下转动，此时系统只受摩擦力矩的作用，根据转动定律则有。

－L 2= J 0β1 （2）（2）式中J 0为本底转动惯量，L 2为摩擦力矩，负号是因L 的方向与外力矩的方向相反，β1为角加速度，计算出β1值应为负值。

（即加适当的重力砝码），则该系统的受力分析如图三所示。

mg －T=ma （3） T ·r －L= J 0β2 （4）a=r β2 （5） 图三 示意图 β2是在外力矩与摩擦力矩的共同作用下，系统的角加速度，r 是 塔轮的半径， ⑵、⑶、⑷、⑸、式联立求解得：由于β1本身是负值所以计算时β2-（-β1）=β2+β1，则（6）应该为：同理加试件后，也可用同样的方法测出J 1……，然后代入（1）式减去本底转动惯量J 0即可得到试件的转动惯量。

用扭摆法测定物体转动惯量刚体定轴转动时，具有以下特征：首先是轴上各点始终静止不动。

其次是轴外刚体上的各个质点，尽管到轴的距离（即转动半径）不同，相同的时间内转过的线位移也不同，但转过的角位移却相同，因此只要在刚体上任意选定一点，研究该点绕定轴的转动并以此来描述刚体的定轴转动。

转动惯量是刚体转动时惯量大小的度量，是表明刚体特性的一个物理量。

刚体转动惯量除了与物体的质量有关外，还与转轴的位置和质量分布（即形状、大小和密度分布）有关。

如果刚体形状简单，且质量分布均匀，可以直接计算出它绕特定转轴的转动惯量。

对于形状复杂，质量分布不均匀的刚体，计算将极为复杂，通常采用实验方法来测定。

一、目的1. 用扭摆测定弹簧的扭转常数和几种不同形状物体的转动惯量和弹簧劲度系数，并与理论值进行比较。

2. 验证转动惯量平行轴定理。

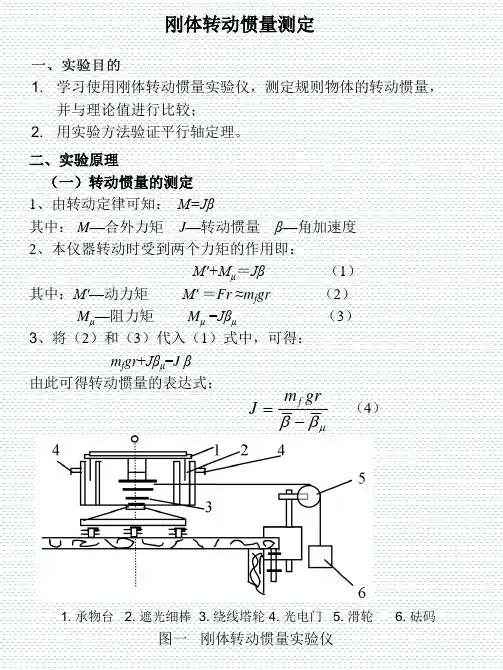
二、原理扭摆的构造见图1所示，在其垂直轴1上装有一根薄 片状的螺旋弹簧2，用以产生恢复力矩。

在轴的上方可以装 上各种待测物体。

垂直轴与支座间装有轴承，使摩擦力矩尽 可能降低。

将物体在水平面内转过一角度θ后，在弹簧的恢复力矩 作用下，物体就开始绕垂直轴作往返扭转运动。

根据虎克定 律，弹簧受扭转而产生的恢复力矩M 与所转过的角度成正 比，即θK M -= （1） 式中，K 为弹簧的扭转常数。

根据转动定律 βI M =式中，I 为物体绕转轴的转动惯量，β为角加速度，由上式得 图 1 IM=β （2） 令IK=2ω，且忽略轴承的摩擦阻力矩，由式（1）与式（2）得 θωθθβ222-=-==I Kdtd上述方程表示扭摆运动具有角简谐振动的特性，即角加速度与角位移成正比，且方向相反。

此方程的解为)cos(ϕωθ+=t A式中，A 为谐振动的角振幅，ϕ为初相位角，ω为角速度。

此谐振动的周期为KIT πωπ22==（3） 利用公式（3）测得扭摆的摆动周期后，在I 和K 中任意一个量已知时即可计算出另一个量。

本实验用一个几何形状有规则的物体，它的转动惯量可以根据它的质量和几何尺寸用理论公式直接计算得到。

刚体转动惯量的测量1. 引言刚体转动惯量是描述刚体绕某一轴旋转时所表现出的惯性特性，它反映了刚体对旋转运动的抵抗能力。

测量刚体转动惯量对于研究物体的旋转运动和确定物体的物理特性具有重要意义。

本文将介绍刚体转动惯量的定义、测量方法以及实验步骤。

2. 刚体转动惯量的定义刚体转动惯量（或称为“转动惯性矩”）是描述刚体绕某一轴旋转时所表现出的抵抗力矩大小的物理量。

它与刚体质量分布和轴线位置相关，可以用数学公式表示为：I=∫r2⋅dm其中，I为刚体相对于旋转轴的转动惯量，r为质点到旋转轴的距离，dm为质点的微小质量。

3. 测量方法3.1 转动定律法利用牛顿第二定律和角加速度与力矩之间的关系，可以通过测定加速度和力矩来计算刚体的转动惯量。

具体步骤如下：1.将待测刚体固定在水平轴上，并使其能够绕该轴自由旋转。

2.在刚体上施加一个垂直于旋转轴的力矩，使刚体产生角加速度。

3.测量施加力矩前后刚体的角加速度，并计算力矩大小。

4.根据牛顿第二定律和角加速度与力矩之间的关系，计算出刚体的转动惯量。

3.2 定滑轮法利用滑轮原理，可以通过测量绕定滑轮旋转的物体的线速度、重物块质量以及滑轮半径来计算刚体的转动惯量。

具体步骤如下：1.将待测刚体固定在定滑轮上，并使其能够自由旋转。

2.在滑轮上挂一重物块，将其与刚体通过一根绳子相连。

3.调整重物块的高度，使得刚体开始自由旋转。

4.测量重物块下降的高度和旋转时间，并记录滑轮半径和重物块质量。

5.根据滑轮原理和动能定理，计算出刚体的转动惯量。

4. 实验步骤4.1 转动定律法实验步骤1.准备实验装置：水平轴、刚体、力矩测量仪器等。

2.将刚体固定在水平轴上，并保证其能够自由旋转。

3.在刚体上施加一个垂直于旋转轴的力矩，使其产生角加速度。

4.使用力矩测量仪器测量施加力矩前后的角加速度，并记录下来。

5.根据牛顿第二定律和角加速度与力矩之间的关系，计算出刚体的转动惯量。

4.2 定滑轮法实验步骤1.准备实验装置：定滑轮、刚体、重物块、绳子等。

第二单元实验1 用扭摆法测刚体转动惯量转动惯量是刚体转动时惯性大小的量度。

刚体的转动惯量与刚体的总质量、形状大小和转轴的位置有关。

对于形状较简单的刚体，可以通过数学方法算出它绕特定轴的转动惯量。

但是对于形状较复杂的刚体，应用数学方法计算它的转动惯量非常困难，故大都用实验方法测定。

刚体的转动惯量在机械动平衡方面有着广泛的应用，凡是涉及往复式直线运动与旋转运动的相互转换，都必须借助具有较大转动惯量的“飞轮”才能实现，其中典型的例子是蒸汽机和内燃机。

此外，为了让机械转动更平稳，最简单的方法就是在其转动轴上加上一个形状规则、质量分布均匀，且具有一定转动惯量的飞轮。

因此，学会刚体转动惯量的测定方法，具有重要的实际意义。

【实验目的】1. 了解ZG-2型转动惯量测定仪测刚体转动惯量的原理和方法。

2. 测定弹簧的扭转常数及几种不同形状刚体的转动惯量。

3. 验证刚体转动的平行轴定理。

【实验原理】1. 弹簧的扭转常数及刚体的转动惯量图1 ZG-2转动惯量测定仪将待测物体在水平面内转过一定角度θ后，在弹簧恢复力矩的作用下，物体就开始绕垂直轴作往返扭转运动。

忽略轴承的摩擦阻力矩，根据虎克定律，弹簧受扭转而产生的恢复力矩M 与所转过的角度θ成正比，即θK M -=（1）式中K 为弹簧的扭转常数。

根据转动定律βI M =式中I 为物体绕转轴的转动惯量，β为角加速度，由此可得θβIK -= （2）令ω2=IK，由(2)式得 -=-==θθβI Kdtd 22ω2θ上述微分方程表示转动惯量仪运动具有角谐振动的特性，即角加速度β与角位移θ成正比，并且方向相反。

此微分方程的解为：)cos(ϕωθ+=t A式中θ为角位移，Ａ为谐振动的角振幅， ϕ为初相位角，ω为圆频率。

此谐振动的周期为KI T πωπ22==则 224T I K π= （3）根据(3)式，只要测得转动惯量仪的摆动周期T ，在I 和K 中任何一个量已知时就可计算出另一个量。

刚体转动惯量的测量一、引言刚体转动惯量是描述刚体旋转惯性的物理量，通常用$I$表示。

测量刚体转动惯量是物理学实验中的重要内容之一，也是学习力学的基础。

本文将介绍刚体转动惯量的测量方法及其原理。

二、刚体转动惯量的定义刚体转动惯量是描述刚体绕某个轴旋转时所表现出来的抵抗力矩大小的物理量。

它可以用下式表示：$$I=\int r^2dm$$其中，$r$为质点到轴线距离，$m$为质点质量。

三、测量方法1. 弹簧振子法弹簧振子法是一种简单易行、精度较高的测量方法。

其原理是利用一个弹簧挂上待测物体，在水平方向上使其偏离平衡位置，并释放后记录振动周期和弹簧伸长长度，通过计算得到刚体转动惯量。

2. 陀螺仪法陀螺仪法利用陀螺仪在空间中保持自身方向不变的特性，将陀螺仪固定在待测物体上，并让其绕轴旋转，通过测量陀螺仪的进动角速度和陀螺仪的自由进动周期来计算刚体转动惯量。

3. 转动台法转动台法是一种较为常见的测量方法，其原理是利用一个转动台将待测物体固定在上面，并通过电机驱动使其绕轴旋转，通过测量电机输出功率和角加速度来计算刚体转动惯量。

四、实验步骤以弹簧振子法为例，具体实验步骤如下：1. 将弹簧挂在水平方向上，等待弹簧稳定后记录其长度$L_0$。

2. 将待测物体挂在弹簧上，并使其偏离平衡位置，记录振动周期$T$和弹簧伸长长度$\Delta L$。

3. 计算物体质量$m$和弹簧劲度系数$k$：$m=\frac{4\pi^2L_0}{gT^2}$，$k=\frac{mg}{\Delta L}$。

4. 计算刚体转动惯量：$I=\frac{kL^2}{4\pi^2}$，其中$L$为待测物体与轴线之间的距离。

五、注意事项1. 实验过程中应注意安全，避免物体脱落或伤人。

2. 测量时应保证待测物体与轴线之间的距离$L$尽可能大，以提高测量精度。

3. 实验数据应多次重复测量，取平均值作为最终结果。

六、总结刚体转动惯量是描述刚体旋转惯性的物理量，其测量方法有多种。

实验4 刚体转动惯量的测定转动惯量的测定，在涉及刚体转动的机电制造、航空、航天、航海、军工等工程技术和科学研究中具有十分重要的意义。

例如在电磁式仪表、发动机叶片、飞轮、陀螺以及人造卫星的外形设计上，都需精确地测定转动惯量。

测定转动惯量常采用扭摆法或恒力矩转动法，本实验采用恒力矩转动法测定转动惯量。

实验目的1. 掌握刚体转动惯量的概念和物理意义；2. 学习用恒力矩转动法测定刚体转动惯量的原理和方法；3. 观测刚体的转动惯量随其质量、质量分布及转轴不同而改变的情况，验证平行轴定理。

实验预习思考题1. 刚体的概念。

2. 刚体转动惯量的概念。

3. 质量分布均匀的常见规则形状刚体（例如杆、圆盘、圆环、圆柱体）的转动惯量计算方法。

4. 刚体的定轴转动定律。

5. 转动惯量实验仪的构成。

6. 实验操作中如何施加的恒力矩？7. 什么是转动惯量的叠加原理？8. 实验中载物台绕中心轴转动的角加速度如何测量？9. 恒力矩转动法测定刚体转动惯量的基本原理。

10. 什么是刚体转动的平行轴定理？实验原理1、转动惯量实验仪转动惯量实验仪如图1所示，绕线塔轮通过特制的轴承安装在主轴上，使转动时的摩擦力矩很小。

载物台用螺钉与塔轮连接在一起，随塔轮转动。

被测试样有1个圆盘，1个圆环，两个圆柱。

圆柱试样可插入载物台上的不同孔内，由内向外半径分别为d1=50mm、d2=75mm。

小滑轮的转动惯量与实验台相比可忽略不记。

仪器的主要参数如下：（1）塔轮半径为15、20、25、30mm共4挡；（2）挂钩（45g）和5g、10g、20g的砝码组合，产生大小不同的力矩；（3）圆盘：质量约486g，半径R=100mm；（4）圆环：质量约460g，外半径R外=100mm，内半径R内=90mm；（5）圆柱体：R=15mm，h=25mm。

图1 转动惯量实验仪2、恒力矩转动法测定转动惯量的原理根据刚体的定轴转动定律：βJ M = (1)只要测定刚体转动时所受的合外力矩M 及该力矩作用下刚体转动的角加速度β，则可计算出该刚体的转动惯量J 。

刚体转动惯量的测量一、实验目的1.学习测量刚体转动惯量的方法。

2.用实验方法验证平行轴定理。

3.用最小二乘法处理数据，进一步熟悉各种数据处理方法。

二、实验仪器刚体转动惯量实验仪，TH-4通用电脑式毫秒计，铝环，铝板，小钢柱，牵引砝码等。

1.刚体转动惯量实验仪刚体转动惯量实验仪如图1所示。

它不但能测定质量分布均匀、断面形状规则刚体的转动惯量，而且能测定质量分布不均匀、断面形状不规则刚体的转动惯量，并可验证物理学的转动定律、平行轴定理等。

它的转动体系由十字形承物台和塔轮组成，可绕它的垂直方向对称轴进行平稳的转动。

两根对称放置的遮光细棒随刚体系统一起转动，依次通过光电门不断遮光。

光电门由发光器件和光敏器件组成，发光器件的电源由毫秒计提供，它们构成一个光电探测器，光电门将细棒每次经过时的遮光信号转变成电脉冲信号，送到通用电脑式毫秒计。

毫秒计记录并存储遮光次数和每次遮光的时刻。

塔轮上有五个不同半径的绕线轮，以提供不同的力臂，从下到上分15mm、20 mm、25 mm、30 mm、35 mm五档。

砝码钩上可以放置不同数量的砝码来改变对转动体系的拉力。

在实验仪十字形承物台每个臂上，沿半径方向等距离d有三个小孔，如图2所示。

小钢柱可以放在这些小孔上，小钢柱在不同的孔位置就改变了它对转动轴的转动惯量，因而也就改变了整个体系的转动惯量，所以可用来验证平行轴定理。

图1 图23通用电脑式毫秒计（左：前面板；右：后面板）2．通用电脑式毫秒计通用电脑式毫秒计是为测量刚体转动惯量而设计的，也可用于物理实验中各种时间测量和计数。

本仪器使用了微电脑（单片机）作为核心器件，它具有记忆功能，最多可记忆九十九组测量时间，并可随时把需要的测量结果取出来。

时间测量有几种方法，可根据需要选择一种。

计时范围0-99.9999s ，计时精度0.1ms 。

两路2.2V 直流电源输出；两路光电门信号或TTL/CMOS 信号电平输入通道；可与计算机通过标准RS232串口通信。