下载文档原格式
2013年全国高中数学联赛一试试题一．填空题：本大题共8小题，每小题8分，共64分。
1.设集合{}3,1,0,2=A ，集合{}A x A x x B ∉-∈-=22,，则集合B 中所有元素的和为2.在平面直角坐标系xOy 中，点A 、B 在抛物线x y 42=上，满足4-=⋅，F 是抛物线的焦点，则OFB OFA S S ∆∆⋅=3.在ABC ∆中，已知C B A C B A cos cos 10cos ,sin sin 10sin ⋅=⋅=，则A tan 的值为4.已知正三棱锥ABC P -的底面边长为1，高为2，则其内切球半径为5.设a 、b 为实数，函数b ax x f +=)(满足：对任意]1,0[∈x ，有1)(≤x f ，则ab 的最大值为6.从20,,2,1⋅⋅⋅中任取5个不同的数，其中至少有2个是相邻数的概率为7.若实数x ，y 满足y x y x -=-24，则x 的取值范围是8.已知数列{}n a 共有9项，其中191==a a ，且对每个{}8,,2,1⋅⋅⋅∈i 均有⎭⎬⎫⎩⎨⎧-∈+21,1,21i i a a ，则这样的数列的个数为二．解答题：本大题共3小题，共56分。
解答应写出文字说明、证明过程或演算步骤。
9.（本题满分16分）给定正数数列{}n x 满足,,3,2,21⋅⋅⋅=≥-n S S n n 这里n n x x S +⋅⋅⋅+=1. 证明：存在常数0>C ,使得⋅⋅⋅=⋅≥,2,1,2n C x n n10.（本题满分20分）在平面直角坐标系xOy 中，椭圆的方程为)0(12222>>=+b a by a x ， 21,A A 分别为椭圆的左、右顶点，21,F F 分别为椭圆的左右焦点，P 为椭圆上不同于1A 和2A 的任意一点.若平面中有两个点R Q ,满足22112211,,,PF RF PF RF PA QA PA QA ⊥⊥⊥⊥, 试确定线段QR 的长度与b 的大小关系，并给出证明。
1总分第十八届华罗庚金杯少年邀请赛决赛试题A （小学中年级组）（时间2013年4月20日10：00～11：30）一、填空题（每小题 10分, 共80分） 1．计算: (2014×2014+2012)-2013×2013________.解析：(2014×2014+2012)-2013×2013=（2013+1）×（2013+1）+2013—1-2013×2013=2013×2013+2013+2013+1+2013-1-2013×2013=6039或用平方差公式。
(2014×2014+2012)-2013×2013=20142-20132+2012=2012+2013+2014=6039 考试中最直接的方法，死算也OK 。
2．将长方形的纸片ABCD 按右图的方式折叠后压平, 使三角形DCF 落在三角形DEF 的位置, 顶点E 恰落在边AB 上. 已知∠1＝20°, 那么∠2是________度.解析：因为翻折，∠CFD=∠EFD=90°-22°=68°∠2=180°-68°-68°=44°3．亮亮上学, 若每分钟行40米, 则8 : 00准时到校; 若每分钟行50米, 则7 : 55到校. 亮亮的家与学校的距离是________米.解析：行程型盈亏问题。
每分钟行40米,刚好够分；若每分钟行50米，则少5×50=250米所以250÷（50-40）=25分钟，亮亮的家与学校的距离是25×40=1000米.法二：六年级可以用。
走同样路程，速度比与时间成反比，速度比为4:5，则时间比为5:4,8:00-7:55=5分钟，则若每分钟行40米,亮亮用时5÷（5-4）×5=25分钟，所以亮亮的家与学校的距离是25×40=1000米.4．第一次操作将图a左下角的正方形分为四个小正方形, 见图b; 第二次操作再将图b左下角的小正方形分为四个更小的正方形, 见图c; 这样继续下去, 当完成第五次操作时, 得到的图形中共有________个正方形.…图b 图c2解析：找规律。
第十八届华罗庚金杯少年邀请赛初赛试题A （初二组）（时间2013年3月23日10：00～11：00） 一、选择题（每题10分，满分60分，以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内。
）1．计算：()1-2127--2-3332+=( ). A ．-1 B ．-1+2 C ．-3-2 D ．-7+2 解析：原式=3-8-（-3）+（12+）= 1-2,选B 。
2． 如果关于x, y 的方程组 3x+4y=m+n-4的解满足0y x =+, 那么mn 的值等于（ ）. x-2y= 3m-2n+3A.0B.1C.2D.3解析：根据根式的意义，可知道x=y=0，可将有关x, y 的方程组转化为m ，n 的方程，解得m=1，n=3，mn 的值等于3，选D 。
3． 如图, 在直角坐标系Oxy 中, A, B 分别是x 轴和y 轴上的点, 四边形OACB是矩形, OA=7, OB=4. 已知反比例函数y=xk （k>0）在第一象限的图象分别与AC, BC 交于F, E. 当△ECF 的面积等于732时, k 的值等于（ ） A ．8 B ．10 C ．12 D ．14解析：根据题意，F, E 在反比例函数y=x k 图象上， E 点坐标（4k ，4），E 点坐标（7，7k ），所以EC=7-4k ,CF=4-7k , S △ECF=732=(7-4k )(4-7k )÷2 化简的k 2-56k+528=0，配方得（k-28）2=256，所以k-28=16，k=12。
答案为C 。
4．如图, 正方形ABCD 中, M, N 是边AB 上的点, E, F 是边CD 上的点, 连接AF, BE,CM, DN 交成四边形PQRS. 若AM = NB = CF = DE = 1, MN = 4. 则四边形PQRS 的面积等于（ ）.A ．53B ．54C ．1D ．56 解析：由对称性,易知PS=SR=RQ=QP ，四边形PQRS 是菱形，不是正方形。
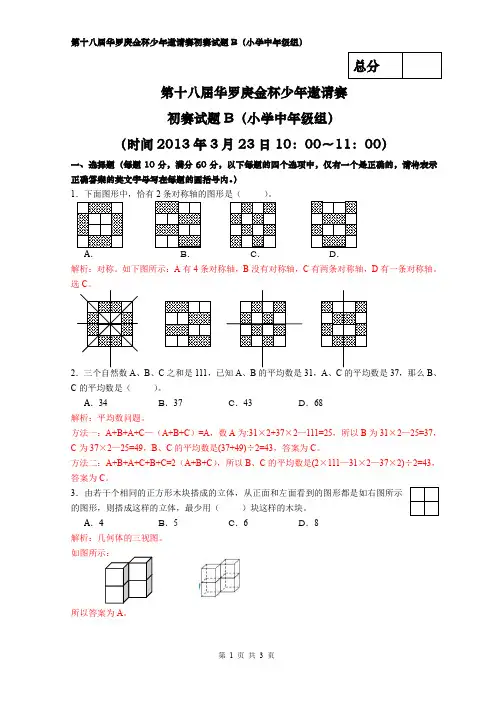
第十八届华罗庚金杯少年邀请赛初赛试题B（小学中年级组）（时间2013年3月23日10：00～11：00）一、选择题（每题10分，满分60分，以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内。
）1．下面图形中，恰有2条对称轴的图形是（）。
解析：对称。
如下图所示：A有4条对称轴，B没有对称轴，C有两条对称轴，D有一条对称轴。
选C。
2．三个自然数A、B、C之和是111，已知A、B的平均数是31，A、C的平均数是37，那么B、C的平均数是（）。
A．34 B．37 C．43 D．68解析：平均数问题。
方法一：A+B+A+C—（A+B+C）=A，数A为:31×2+37×2—111=25，所以B为31×2—25=37，C为37×2—25=49，B、C的平均数是(37+49)÷2=43，答案为C。
方法二：A+B+A+C+B+C=2（A+B+C），所以B、C的平均数是(2×111—31×2—37×2)÷2=43，答案为C。
3．由若干个相同的正方形木块搭成的立体，从正面和左面看到的图形都是如右图所示的图形，则搭成这样的立体，最少用（）块这样的木块。
A．4 B．5 C．6 D．8解析：几何体的三视图。
所以答案为A。
4．在七个三角形的所有内角中，有两个直角，三个钝角，那么这些三角形中有（ ）个锐角三角形。
A ．1B ．2C ．3D ．4解析：三角形七个三角形的21内角中，有两个直角，三个钝角，则这七个三角形中，有两个直角三角形，三个钝角三角形，剩余2个是锐角三角形。
选B 。
5．把自然数按右图所示的方法排列，那么排在第10行第5列的数是（ ）。
A ．79B ．87C ．94D ．101解析：数列数组。
方法一：找规律第一列：后一个数比前一个数依次增加2，3，4，5，…第二列：后一个数比前一个数依次增加3，4，5，6，…第三列：后一个数比前一个数依次增加4，5，6，7，……第一行：后一个数比前一个数依次增加1，2，3，4，5，…第二行：后一个数比前一个数依次增加2，3，4，5，6，…第三行：后一个数比前一个数依次增加3，4，5，6，7，……所以第10行第5列的数是1+（1+2+3+4）+（6+7+8+…+14）=（1+14）×14÷2—5＋1=101或1+（2+3+4+…+10）+( 10+11+12+13)= （1+13）×13÷2＋10=101方法二：我们把斜行称为组，则每组数的个数依次是1，2，3，4…，注意每个数的行序数、列序数、组序数之间有一个规律：行序数+列序数=组序数+1，因此，第10行第5列的数是第14组的第10个数（每组数都是从右往左排列），即（1+13）×13÷2＋10=101，选D 。
2013年全国高中数学联赛一试试题一．填空题：本大题共8小题，每小题8分，共64分。
1.设集合{}3,1,0,2=A ，集合{}A x A x xB ∉-∈-=22,，则集合B 中所有元素的和为 2.在平面直角坐标系xOy 中，点A 、B 在抛物线x y 42=上，满足4-=⋅OB OA ，F 是抛物线的焦点，则OFB OFA S S ∆∆⋅=3.在ABC ∆中，已知C B A C B A cos cos 10cos ,sin sin 10sin ⋅=⋅=，则A tan 的值为4.已知正三棱锥ABC P -的底面边长为1，高为2，则其内切球半径为5.设a 、b 为实数，函数b ax x f +=)(满足：对任意]1,0[∈x ，有1)(≤x f ，则ab 的最大值为6.从20,,2,1⋅⋅⋅中任取5个不同的数，其中至少有2个是相邻数的概率为7.若实数x ，y 满足y x y x -=-24，则x 的取值范围是8.已知数列{}n a 共有9项，其中191==a a ，且对每个{}8,,2,1⋅⋅⋅∈i 均有⎭⎬⎫⎩⎨⎧-∈+21,1,21i i a a ，则这样的数列的个数为二．解答题：本大题共3小题，共56分。
解答应写出文字说明、证明过程或演算步骤。
9.（本题满分16分）给定正数数列{}n x 满足,,3,2,21⋅⋅⋅=≥-n S S n n 这里n n x x S +⋅⋅⋅+=1. 证明：存在常数0>C ,使得⋅⋅⋅=⋅≥,2,1,2n C x n n 10.（本题满分20分）在平面直角坐标系xOy 中，椭圆的方程为)0(12222>>=+b a by a x ，21,A A 分别为椭圆的左、右顶点，21,F F 分别为椭圆的左右焦点，P 为椭圆上不同于1A 和2A 的任意一点.若平面中有两个点R Q ,满足22112211,,,PF RF PF RF PA QA PA QA ⊥⊥⊥⊥, 试确定线段QR 的长度与b 的大小关系，并给出证明。
第十八届华罗庚金杯少年邀请赛 决赛试题C （小学高年级组）（时间2013年4月20日10：00～11：30）一、填空题（每小题 10分, 共80分） 1．计算:278)]51111()11131(322[÷+÷-⨯ =________.解析：原式=2785516338322÷÷⨯=827165533838⨯⨯⨯=2172． 农谚‘逢冬数九’讲的是, 从冬至之日起, 每九天分为一段, 依次称之为一九, 二九, ……, 九九, 冬至那天是一九的第一天. 2012年12月21日是冬至, 那么2013年2月3日是________九的第________天.解析：31-21+1+31+3=45,45÷9=5 ，2013年的2月3日是五九的第9天. 3．最简单分数ba 满足41ba 51<<, 且b 不超过19, 那么a+b 的最大可能值与最小可能值之积为________. 解析：通分子得a4a b a a5a <<，4a<b<5a, b 不超过19，所以a 最大值为4，此时b 最大可为19，当a=2时，b 有最小值9，a+b 的最大可能值与最小可能值之积为（4+19）×（2+9）=253。
4．如图所示, P, Q 分别是正方形ABCD 的边AD 和对角线 AC 上的点, 且AP:PD=1：3，AQ:QC=4：1, 如果正方形ABCD 的面积为100, 那么三角形PBQ 的面积是________. 解析：连接QD,做QE ⊥BC 于E, QF ⊥AD 于F, QG ⊥CD 于G, 正方形ABCD 的面积为100,所以AD=EF=10， QC: AQ =1:4,根据正方形对称性，所以QE=QG=2，QF=8, PD:AP =3:1, AP=2.5，PD=7.5。
S △PQB=S 正- S △CQB-S △DQC-S △PQD-S △PAB=100-2×10÷2×2-8×7.5÷2-10×2.5÷2 =100-20-30-12.5 =37.55．四位数abcd 与cdab 的和为3333, 差为693, 那么四位数abcd 为________. 解析：abcd +cdab =101（ab +cd ），所以ab +cd =3333÷101=33，abcd -cdab =99（ab -cd ），所以ab +cd=693÷99=7，所以ab =20，cd =13，abcd =2013。
第十八届华罗庚金杯少年邀请赛
初赛试题A（小学高年级组）
（时间2013年3月23日10：00～11：00）
一、选择题（每题10分，满分60分，以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内。
）
1．2012.25×2013.75－2010.25×2015.75＝（）。
A．5 B．6 C．7 D．8
解析：巧算问题
原式=（2010.25+2）×（2015.75-2）－2010.25×2015.75
=2015.75×2－2010.25×2－4
=7
答案为C。
2．2013年的钟声敲响了, 小明哥哥感慨地说: 这是我有生以来第一次将要渡过一个没有重复数字的年份。
已知小明哥哥出生的年份是19的倍数, 那么2013年小明哥哥的年龄是（）岁。
A．16 B．18 C．20 D．22
解析：简单数论。
从1990年～2012年，年份中都有重复数字，其中是19的倍数的数只有1900+95=1995，2012—1995=18（岁），所以选B。
3．一只青蛙8点从深为12米的井底向上爬, 它每向上爬3米, 因为井壁打滑, 就会下滑1米, 下滑1米的时间是向上爬3米所用时间的三分之一。
8点17分时, 青蛙第二次爬至离井口3米之处, 那么青蛙从井底爬到井口时所花的时间为（）分钟。
A．22 B．20 C．17 D．16
解析：周期问题。
下滑1米的时间是向上爬3米所用时间的三；爬一米和滑一米的时间相同，以爬三米，滑一米为一个周期；（3-1）×3+3=9m,青蛙第一次爬至离井口3米之处，（3-1）×4+1=9m，青蛙第二次爬至离井口3米之处，此时，青蛙爬了4个周期加1米，用时17分钟，所以青蛙每爬1m或滑1m所用时间为1分钟。
（12—3）÷（3-1）=4…1，青蛙从井底爬到井口经过5个周期，再爬2m，用时5×（3+1）+2=22分钟，选A。
4．一个盒子里有黑棋子和白棋子若干粒, 若取出一粒黑子, 则余下的黑子数与白子数之比为9:7, 若放回黑子, 再取出一粒白子, 则余下的黑子数与白子数之比为7:5, 那么盒子里原有的
黑子数比白子数多（）个。
A．5 B．6 C．7 D．8
解析：比和比例。
关键是找不变量，两次操作剩余棋子的总量不变。
取一颗黑子：黑子：白字：剩余棋子和=9:7:16
取一颗白子：黑子：白字：剩余棋子和=7:5:12
[12，16]=48
9:7:16=27:21:48，7:5:12=28:20:48，所以原来有黑棋子28颗，白棋子21颗，所以黑子数比白子数多28-21=7颗。
选C。
5．右图ABCD 是平行四边形, M 是DC 的中点, E 和F 分别位于AB 和AD 上,
且EF 平行于BD 。
若三角形MDF 的面积等于5平方厘米, 则三角形CEB 的面积等于（ ）平方厘米。
A ．5
B ．10
C ．15
D ．20 解析：面积问题，梯形的蝶形翅膀
如图：连接FC,DE,FB,在梯形FBCD 中，有S △FDB=S △FDC,
在梯形EBCD 中，有S △EDB=S △EBC, 在梯形FEBD 中，有S △FDB=S △EDB, 所以S △FDC= S △EBC ，因为M 是DC 的中点，所以S △EBC=2×5=10cm 2。
答案为B 。
6．水池A 和B 同为长3米, 宽2米, 深1.2米的长方体。
1号阀门用来向A 池注水, 18分钟可将无水的A 池注满; 2号阀门用来从A 池向B 池放水, 24分钟可将A 池中满池水放入B 池。
若同时打开1号和2号阀门, 那么当A 池水深0.4米时, B 池有（ ）立方米的水。
A ．0.9
B ．1.8
C ．3.6
D ．7.2 解析：进出水工程问题。
设水池A 和B 的容积为“1”，1号阀门A 池每分钟进水效率
181，2号阀门B 池每分钟进水效率24
1，A 池每分钟放水效率也是241，同时打开1号和2号阀门，则A 池每分钟进水效率为721
241-181=
，B 池每分钟进水效率241。
A 池水深0.4米，则A 池进水0.4÷1.2= 31，需要时间24721
31=÷分钟，
B 池进水24×24
1=1，所以B 池有水3×2×1.2=7.2m 3。
答案为D 。
二、填空题(每小题 10 分, 满分40分)
7． 小明、小华、小刚三人分363张卡片, 他们决定按年龄比来分。
若小明拿7张, 小华就要拿6张；若小刚拿8张, 小明就要拿5张。
最后, 小明拿了________张；小华拿了________张；小刚拿了________张。
解析：连比和按比例分配。
小明, 小华，小刚拿卡片的张数比为 (7×5):(6×5):(8×7)=35:30:56
所以小明拿了363÷（35+30+56）×35=105张，小华拿了363÷（35+30+56）×30=90张，小明拿了363÷（35+30+56）×56=168张。
8．某公司的工作人员每周都工作5天休息2天, 而公司要求每周从周一至周日, 每天都至少有32人上班, 那么该公司至少需要________名工作人员。
解析：最值，抽屉原理问题。
根据题意，该公司一周总上班人次至少为32×7=224（人次），而每人每周上
5人次，
224÷5=44…4，所以至少需要44+1=45人。
9．右图中, AB 是圆O 的直径, 长6厘米, 正方形BCDE 的一个顶点E 在圆周
上,∠ABE=45°。
那么圆O 中非阴影部分的面积与正方形BCDE 中非阴影部分面积的差等于________平方厘米（取π=3.14） 解析：图形面积,差不变问题。
圆O 中非阴影部分的面积-正方形BCDE 中非阴影部分面积=（圆O 中非阴影部分的
面积+阴影部分面积）-（正方形BCDE 中非阴影部分面积+阴影部分面积）=S 圆-S
正。
关键是求正方形的面积，如图，连接EO ，S 正=EB ×EB=EO 2+BO 2=(6÷2)2×2=18cm 2
所以圆O 中非阴影部分的面积与正方形BCDE 中非阴影部分面积的差:
A B
E C
D F A B
E C F
O B
D E
O B
D E
π×(6÷2)2-18=10.28cm2.
10．圣诞老人有36个同样的礼物, 分别装在8个袋子中。
已知8个袋子中礼物的个数至少为1且各不相同。
现要从中选出一些袋子, 将选出的袋子中的所有礼物平均分给8个小朋友, 恰好分完（每个小朋友至少分得一个礼物）。
那么, 共有________种不同的选择。
解析：数论问题，整数拆分。
做出这个题，需要有点数感，36个同样的礼物装在8个袋子中，每个袋子礼物的个数至少为1且各不相同，而1+2+3+…+8=（1+8）×8÷2=36，明确8个袋子分别装的礼物数是1～8。
根据题意要求选出袋子里装的礼物数为8的倍数，分情况枚举即可。
如果每人分1个礼物：8=8
=1+7=2+6=3+5
=1+2+5=1+3+4,6种；
如果每人分2个礼物：16=1+7+8=2+6+8=3+5+8=4+5+7
=1+2+5+8=1+2+6+7=1+3+4+8=1+3+5+7=1+4+5+6=2+3+4+7=2+3+5+6
=1+2+3+4+6，共13种；
如果每人分3个礼物，拆分24，与拆分36-24=12是一样的。
12=4+8=5+7
=1+3+8=1+4+7=1+5+6=2+3+7=2+4+6=3+4+5
=1+2+3+6=1+2+4+5，共10种；
如果每人分4个礼物，同理拆分36-32=4
4=4=1+3，共2种；
所以，共有 6+13+10+2=31种不同的选择。
本题关键是枚举要有序，不重复不遗漏！。
