初中数学-八年级数学-一次函数的概念及图像专题讲义
- 格式:pdf
- 大小:256.11 KB
- 文档页数:8

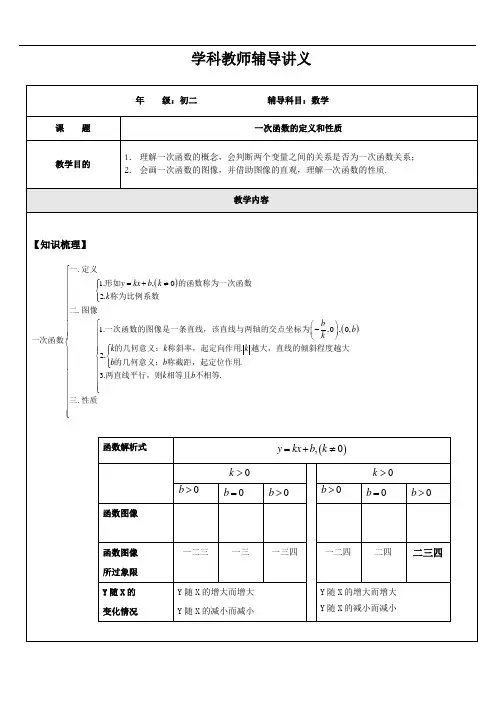









一次函数的图像及性质一:一次函数的概念1、一次函数的概念(1)一般地,解析式形如y kx b =+(k ,b 是常数,且0k ≠)的函数叫做一次函数;(2)一次函数y kx b =+的定义域是一切实数;(3)当0b =时,解析式y kx b =+就成为y kx =(k 是常数,且0k ≠)这时,y 是x 的正比例函数,所以正比例函数是一次函数的特例;(4)一般地,我们把函数y c =(c 为常数)叫做常值函数.它的自变量由所讨论的问题确定.【例1】下列函数中,哪些是一次函数?(1)232y x =-;(2)12y x -=;(3)(5)(0)y m x m =-≠;(4)1(0)y ax a a =+≠;(5)(0)k y kx k x =+≠;(6)(3)(3)y k x k =-+≠-.【例2】(1)已知函数2(2)1y k x =-+是一次函数,则k 的取值范围是_________;(2)当m =________时,函数215(4)m y x m -=+-是一次函数,且不是正比例函数.【例3】已知一个一次函数,当自变量2x =-时,函数值为1y =-;当2x =时,11y =.求这个函数的解析式.【例4】已知一次函数()23317k k y k x -+=-+是一次函数,求实数k 的值.【例5】若()f x 是一次函数,且[()]87f f x x =+,求()f x 的解析式.二:一次函数的图像1、一次函数的图像:一般地,一次函数y kx b =+(k ,b 是常数,且0k ≠)的图像是一条直线.一次函数y kx b =+的图像也称为直线y kx b =+,这时,我们把一次函数的解析式y kx b =+称为这一直线的表达式.画一次函数y kx b =+的图像时,只需描出图像上的两个点,然后过这两点作一条直线.2、一次函数的截距:一条直线与y 轴的交点的纵坐标叫做这条直线在y 轴上的截距,简称直线的截距,一般地,直线y kx b =+(0k ≠)与y 轴的交点坐标是(0)b ,,直线y kx b =+(0k ≠)的截距是b .3、一次函数图像的平移:一般地,一次函数y kx b =+(0b ≠)的图像可由正比例函数y kx =的图像平移得到.当0b >时,向上平移b 个单位;当0b <时,向下平移b 个单位.(函数平移口诀简记为:“上加下减,左加右减”)4、直线位置关系:如果12b b ≠,那么直线1y kx b =+与直线2y kx b =+平行.反过来,如果直线11y k x b =+与直线22y k x b =+平行,那么12k k =,12b b ≠.【例7】若一次函数2(3)(9)y a x a =-+-函数图像过原点,求a 的值,并在坐标系中画出函数的图像.【例8】若一次函数y kx b =+,当x =2时,y =-1,且函数图像的截距为-3,求函数的解析式.【例9】若一次函数y =-x +b 的图像的截距是-4,求将这个一次函数向左平移2个单位后的函数解析式.【例10】将直线y =x +1向右平移1个单位,相当于将直线y =x +1向上平移了多少个单位?【例11】已知一次函数的图像平行于直线y =23x ,且当3x =-时,函数y 的值是1,求这个函数解析式.【例12】若直线2(3)(21)y m x m =-++与直线23y x =-+平行,求m 的值.【例13】根据下列条件,求解相应的直线表达式.(1)直线经过(3,2)以及(1,1);(2)直线经过(7,0)以及截距是14;(3)直线经过(30)-,以及截距是【例14】直线2(13)(22)y k x k =-+-与已知直线21y x =-+平行,且不经过第三象限,求k 的值.【例15】设点P (3,m ),Q (n ,2)都在函数y =x +b 的图象上,求m +n 的值.【例16】已知一次函数21544m y x +=-与233m y x =-+的图像在第四象限内交于一点,求整数m 的值.【例17】已知两个一次函数144b y x =--和212y x a a=+;(1)a 、b 为何值时,两函数的图像重合?(2)a 、b 满足什么关系时,两函数的图像相互平行?(3)a 、b 取何值时,两函数图像交于x 轴上同一点,并求这一点的坐标.【例18】(1)一次函数3y x b =+的图象与两坐标轴围成的三角形的面积为48,求b 的值;(2)一次函数y kx b =+的图像与两坐标围成的三角形的面积是10,截距是,求一次函数的解析式.【例19】(1)求直线14222y x y x =-=+和与y 轴所围成的三角形的面积;(2)求直线24y x =-与直线31y x =-+与x 轴所围成的三角形的面积.【例20】如图,已知由x 轴、一次函数4(0)y kx k =+<的图像及分别过点C (1,0)、D (4,0)两点作平行于y 轴的两条直线所围成的图形ABDC 的面积为7,试求这个一次函数的解析式.三:一次函数的性质1、一次函数的增减性:一般地,一次函数y kx b =+(,k b 为常数,0k ≠)具有以下性质:当0k >时,函数值y 随自变量x 的值增大而增大,图像为上升;当0k <时,函数值y 随自变量x 的值增大而减小,图像为下降.2、一次函数图像的位置情况:直线y kx b =+(0k ≠,0b ≠)过(0,)b 且与直线y kx =平行,由直线y kx =在平面直角坐标系内的位置情况可知:(要用图像的平移推导可得)当0k >,且0b >时,直线y kx b =+经过一、二、三象限;当0k >,且0b <时,直线y kx b =+经过一、三、四象限;当0k <,且0b >时,直线y kx b =+经过一、二、四象限;当0k <,且0b <时,直线y kx b =+经过二、三、四象限.【例22】如果一次函数y =kx +b 的图象经过第一象限,且与y 轴负半轴相交,那么()A .0k >,0b >B .0k >,b <0C .0k <,b >0D .0k <,0b <【例23】一次函数y =-2x +3的图象不经过的象限是()A.第一象限 B.第二象限 C.第三象限D.第四象限【例24】根据下列条件填空:(1)已知函数245(1)(3)m m y m x m -+=-+-,当m 等于______时,它是一次函数,此时它的图象经过__________象限,y 随x 的增大而_____________;(2)如果一次函数2y x =和y x k =+的图象的交点在第一象限,则k 的取值范围是_________;(3)已知关于x 的一次函数(27)2y a x a =-+-的图象与y 轴的交点在x 轴的上方,且y 随x 的增大而减小,则a 的取值范围是________________.【例25】已知0abc ≠,而且a b b c c a p c a b +++===,那么直线y px p =+一定经过()A 、第一、二象限;B 、第二、三象限;C 、第三、四象限;D 、第一、四象限【例26】在式子()y kx b k b =+,为常数中,3119x y -≤≤≤≤当时,,kb 求的值.【课后练习】1.已知:2231()3m m y m m x m -+=-+-是一次函数,则m =_________.2.已知一次函数y kx b =+(0k ≠),把它的图像向右平移3个单位,再向下平移5个单位,所得到的图像与原来的图像重合,则k =___________.3.已知23(2)1m y m x m -=++-表示关于x 的一次函数;(1)求函数解析式;(2)求(10)f ,1()2f -的值;(3)如果()4f a =,求实数a .4.若直线23y mx m =++的截距是4,且y 随x 的增大而减小,求该直线的函数解析式.5.若00b c a a<>,,请指出一次函数y abx ac =+的图像所经过的象限.6.已知一次函数(1)4y m x m =-+-不经过第二象限,求m 的取值范围.7.已知一次函数y kx b =+(0k ≠)与x 轴、y 轴围成的三角形面积为24,且与直线4733y x =-平行,求此一次函数的解析式.8.直线1l :y kx b =+过点B (-1,0)与y 轴交于点C ,直线2l :y mx n =+与1l 交于点P (2,5)且过点A (6,0),过点C 与2l 平行的直线交x 轴于点D ;(1)求直线CD 的函数解析式;(2)求四边形APCD 的面积.9.直线313y x =-+与x 轴、y 轴分别交于点A 、点B ,以线段AB 为直角边在第一象限内作等腰Rt ABC ∆,且90BAC ∠= ,如果在第二象限内有一点P (a ,12),且ABP ∆的面积与Rt ABC ∆的面积相等,求a 的值.10.一次函数(2)3y k x k =-+-的图像能否可以不经过第三象限?为什么?11.已知直线26x y k -=-+和341x y k +=+,若它们的交点第四象限,那么k 的取值范围是______________.12.如图,据函数y kx b =+的图像,填空:(1)当1x =-时,y =____________;(2)图像与坐标轴的交点坐标是_________________;(3)当24x -≤≤时,y 的取值范围是______________.xy 2-4O。