第七章贝叶斯网络

贝叶斯网络的参数敏感性分析引言贝叶斯网络是一种概率图模型，它能够描述和处理不确定性信息。

在许多领域，如医学诊断、工程设计和金融风险管理中，贝叶斯网络都得到了广泛的应用。

在实际应用中，贝叶斯网络的参数选择对于网络的性能和可靠性起着至关重要的作用。

因此，对于贝叶斯网络的参数敏感性进行分析是非常重要的。

贝叶斯网络的基本原理贝叶斯网络是一种用来描述随机变量之间的依赖关系的图模型。

它由两部分组成：一个有向无环图(DAG)和每个节点的概率分布。

DAG用来表示变量之间的依赖关系，而每个节点的概率分布则表示了给定父节点的情况下，该节点的概率分布。

贝叶斯网络可以用来进行概率推理和决策分析，它能够有效地处理不确定性信息。

参数敏感性分析方法在实际应用中，贝叶斯网络的参数选择对于网络性能和可靠性至关重要。

参数敏感性分析是指在给定一些参数的情况下，分析其他参数对网络输出的影响程度。

参数敏感性分析可以帮助我们确定哪些参数对网络的性能影响最大，从而有针对性地进行参数调整和优化。

常见的参数敏感性分析方法包括：单参数敏感性分析、多参数敏感性分析和全局敏感性分析。

单参数敏感性分析是指在给定其他参数的情况下，分析某一参数对网络输出的影响程度。

多参数敏感性分析则是考虑多个参数的影响，分析它们之间的相互作用。

全局敏感性分析则是对整个参数空间进行分析，考虑所有参数对网络输出的影响程度。

应用案例为了更好地理解贝叶斯网络的参数敏感性分析，我们以医学诊断为例进行说明。

假设我们有一个用于肺癌诊断的贝叶斯网络模型，其中包括症状、体征和检查结果等变量。

我们可以进行参数敏感性分析，分析各个参数对诊断结果的影响程度。

通过参数敏感性分析，我们可以确定哪些参数对诊断结果的影响最大，从而有针对性地进行调整和优化。

结论贝叶斯网络是一种能够有效处理不确定性信息的概率图模型，在实际应用中得到了广泛的应用。

对于贝叶斯网络的参数敏感性进行分析是非常重要的，它可以帮助我们确定哪些参数对网络的性能影响最大，从而有针对性地进行参数调整和优化。

贝叶斯网络2007-12-27 15:13贝叶斯网络贝叶斯网络亦称信念网络(Belief Network)，于1985 年由Judea Pearl 首先提出。

它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。

它的节点用随机变量或命题来标识，认为有直接关系的命题或变量则用弧来连接。

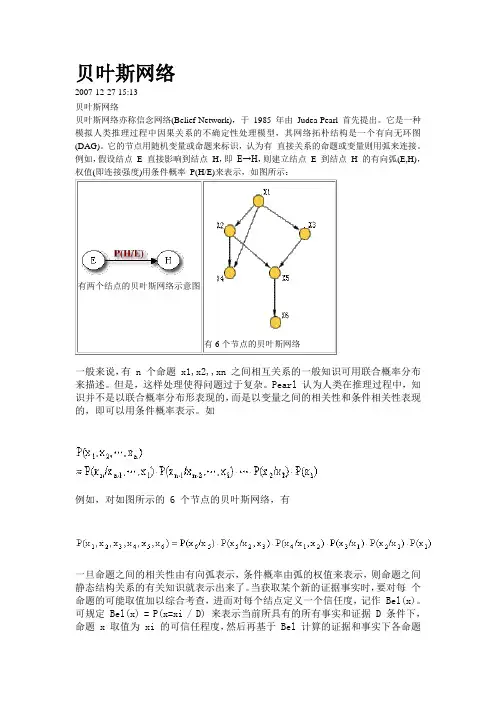
例如，假设结点E 直接影响到结点H，即E→H，则建立结点E 到结点H 的有向弧(E,H)，权值(即连接强度)用条件概率P(H/E)来表示，如图所示：一般来说，有 n 个命题 x1,x2,,xn 之间相互关系的一般知识可用联合概率分布来描述。

但是，这样处理使得问题过于复杂。

Pearl 认为人类在推理过程中，知识并不是以联合概率分布形表现的，而是以变量之间的相关性和条件相关性表现的，即可以用条件概率表示。

如例如，对如图所示的 6 个节点的贝叶斯网络，有一旦命题之间的相关性由有向弧表示，条件概率由弧的权值来表示，则命题之间静态结构关系的有关知识就表示出来了。

当获取某个新的证据事实时，要对每个命题的可能取值加以综合考查，进而对每个结点定义一个信任度，记作 Bel(x)。

可规定 Bel(x) = P(x=xi / D) 来表示当前所具有的所有事实和证据 D 条件下，命题 x 取值为 xi 的可信任程度，然后再基于 Bel 计算的证据和事实下各命题的可信任程度。

团队作战目标选择在 Robocode 中，特别在团队作战中。

战场上同时存在很多机器人，在你附近的机器人有可能是队友，也有可能是敌人。

如何从这些复杂的信息中选择目标机器人，是团队作战的一大问题，当然我们可以人工做一些简单的判断，但是战场的信息是变化的，人工假定的条件并不是都能成立，所以让机器人能自我选择，自我推理出最优目标才是可行之首。

而贝叶斯网络在处理概率问题上面有很大的优势。

首先，贝叶斯网络在联合概率方面有一个紧凑的表示法，这样比较容易根据一些事例搜索到可能的目标。

3．5 贝叶斯网络贝叶斯网络是一系列变量的联合概率分布的图形表示。

一般包含两个部分，一个就是贝叶斯网络结构图，这是一个有向无环图（DAG），其中图中的每个节点代表相应的变量，节点之间的连接关系代表了贝叶斯网络的条件独立语义。

另一部分，就是节点和节点之间的条件概率表（CPT），也就是一系列的概率值。

如果一个贝叶斯网络提供了足够的条件概率值，足以计算任何给定的联合概率，我们就称，它是可计算的，即可推理的。

3.5。

1 贝叶斯网络基础首先从一个具体的实例（医疗诊断的例子）来说明贝叶斯网络的构造。

假设：命题S(moker）:该患者是一个吸烟者命题C（oal Miner)：该患者是一个煤矿矿井工人命题L（ung Cancer)：他患了肺癌命题E（mphysema）：他患了肺气肿命题S对命题L和命题E有因果影响，而C对E也有因果影响.命题之间的关系可以描绘成如右图所示的因果关系网.因此，贝叶斯网有时也叫因果网，因为可以将连接结点的弧认为是表达了直接的因果关系.图3-5 贝叶斯网络的实例图中表达了贝叶斯网的两个要素：其一为贝叶斯网的结构，也就是各节点的继承关系,其二就是条件概率表CPT。

若一个贝叶斯网可计算，则这两个条件缺一不可。

贝叶斯网由一个有向无环图（DAG)及描述顶点之间的概率表组成。

其中每个顶点对应一个随机变量。

这个图表达了分布的一系列有条件独立属性：在给定了父亲节点的状态后,每个变量与它在图中的非继承节点在概率上是独立的。

该图抓住了概率分布的定性结构，并被开发来做高效推理和决策。

贝叶斯网络能表示任意概率分布的同时,它们为这些能用简单结构表示的分布提供了可计算优势。

假设对于顶点xi，其双亲节点集为Pai,每个变量xi的条件概率P（xi｜Pai). 则顶点集合X={x1，x2,…，xn}的联合概率分布可如下计算：.双亲结点。

该结点得上一代结点。

该等式暗示了早先给定的图结构有条件独立语义。

它说明贝叶斯网络所表示的联合分布作为一些单独的局部交互作用模型的结果具有因式分解的表示形式。

概率图模型中的贝叶斯网络建模方法解析概率图模型是用概率论的方法来描述随机变量之间的依赖关系的数学模型。

而在概率图模型中，贝叶斯网络是其中的一种重要模型，它能够描述随机变量之间的条件依赖关系，并且在许多实际问题中有着广泛的应用。

在本文中，我们将对贝叶斯网络的建模方法进行深入解析，包括网络结构的构建、参数的学习以及推断的方法等内容。

贝叶斯网络是一种有向无环图，它由节点和有向边组成，每个节点表示一个随机变量，有向边表示变量之间的依赖关系。

在贝叶斯网络中，节点的依赖关系是通过条件概率来描述的，每个节点的条件概率都是在给定其父节点条件下该节点的概率分布。

因此，贝叶斯网络可以很直观地表示变量之间的条件依赖关系，这也是它在实际问题中得到广泛应用的原因之一。

在构建贝叶斯网络时，首先需要确定网络的结构。

网络的结构可以通过领域知识、数据分析等方法来确定。

一般来说，如果已经有了一定的领域知识，可以通过专家的经验来确定网络的结构；如果没有足够的领域知识，可以通过数据分析的方法来确定网络的结构。

在确定网络结构后，接下来就是确定网络中每个节点的条件概率分布。

确定节点的条件概率分布是贝叶斯网络建模中的一个重要步骤。

在确定节点的条件概率分布时，可以利用领域知识、数据分析等方法来确定。

如果已经有了一定的领域知识，可以通过专家的经验来确定节点的条件概率分布；如果没有足够的领域知识，可以通过数据分析的方法来确定节点的条件概率分布。

在确定了网络的结构和节点的条件概率分布后，就可以对网络进行参数的学习。

参数的学习是指利用已有的数据来确定网络中每个节点的条件概率分布。

在参数的学习中，一般采用最大似然估计或者贝叶斯估计等方法来确定节点的条件概率分布。

最大似然估计是通过最大化数据的似然函数来确定参数，而贝叶斯估计是基于贝叶斯定理来确定参数。

在参数的学习中，需要考虑到数据的稀疏性、噪声等因素，以确保学到的参数能够较好地描述数据。

参数学习完成后，就可以利用贝叶斯网络进行推断。

贝叶斯网络结构学习总结一、 贝叶斯网络结构学习的原理从数据中学习贝叶斯网络结构就是对给定的数据集，找到一个与数据集拟合最好的网络。

首先定义一个随机变量hS ，表示网络结构的不确定性，并赋予先验概率分布()h p S 。

然后计算后验概率分布(|)h p S D 。

根据Bayesian 定理有(|)(,)/()()(|)/()h h h h p S D p S D p D p S p D S p D ==其中()p D 是一个与结构无关的正规化常数，(|)h p D S 是边界似然。

于是确定网络结构的后验分布只需要为每一个可能的结构计算数据的边界似然。

在无约束多项分布、参数独立、采用Dirichlet 先验和数据完整的前提下，数据的边界似然正好等于每一个（i ，j ）对的边界似然的乘积，即111()()(|)()()iiq r n ij ijk ijk hi j k ij ij ijk N p D S N ===Γ∂Γ∂+=Γ∂+Γ∂∏∏∏二、 贝叶斯网络完整数据集下结构学习方法贝叶斯网络建模一般有三种方法：1）依靠专家建模；2）从数据中学习；3）从知识库中创建。

在实际建模过程中常常综合运用这些方法，以专家知识为主导，以数据库和知识库为辅助手段，扬长避短，发挥各自优势，来保证建模的效率和准确性。

但是，在不具备专家知识或知识库的前提下，从数据中学习贝叶斯网络模型结构的研究显得尤为重要。

常用的结构学习方法主要有两类，分别是基于依赖性测试的学习和基于搜索评分的学习。

第一类方法是基于依赖性测试的方法，它是在给定数据集D 中评估变量之间的条件独立性关系，构建网络结构。

基于条件独立测试方法学习效率最好，典型的算法包括三阶段分析算法（TPDA ）。

基于依赖性测试的方法比较直观，贴近贝叶斯网络的语义，把条件独立性测试和网络结构的搜索分离开，不足之处是对条件独立性测试产生的误差非常敏感。

且在某些情况下条件独立性测试的次数相对于变量的数目成指数级增长。

贝叶斯网络贝叶斯网络（Bayesian network），又称信念网络（belief network）或是有向无环图模型（directed acyclic graphical model），是一种概率图型模型，借由有向无环图（directed acyclic graphs, or DAGs）中得知一组随机变数{}及其n组条件概率分配（conditional probability distributions, or CPDs）的性质。

举例而言，贝叶斯网络可用来表示疾病和其相关症状间的概率关系；倘若已知某种症状下，贝叶斯网络就可用来计算各种可能罹患疾病之发生概率。

一般而言，贝叶斯网络的有向无环图中的节点表示随机变数，它们可以是可观察到的变量，抑或是隐变量、未知参数等。

连接两个节点的箭头代表此两个随机变数是具有因果关系或是非条件独立的；而两个节点间若没有箭头相互连接一起的情况就称其随机变数彼此间为条件独立。

若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因（parents）”，另一个是“果（descendants or children）”，两节点就会产生一个条件概率值。

比方说，我们以表示第i个节点，而的“因”以表示，的“果”以表示；图一就是一种典型的贝叶斯网络结构图，依照先前的定义，我们就可以轻易的从图一可以得知：，以及大部分的情况下，贝叶斯网络适用在节点的性质是属于离散型的情况下，且依照此条件概率写出条件概率表（conditional probability table, or CPT），此条件概率表的每一行（row）列出所有可能发生的，每一列（column）列出所有可能发生的，且任一行的概率总和必为1。

写出条件概率表后就很容易将事情给条理化，且轻易地得知此贝叶斯网络结构图中各节点间之因果关系；但是条件概率表也有其缺点：若是节点是由很多的“因”所造成的“果”，如此条件概率表就会变得在计算上既复杂又使用不便。

贝叶斯网络（Ⅰ）本章正式介绍不确定推理的贝叶斯网络，也叫概率网络或者信度网络。

在很多应用领域中贝叶斯网络都是一个强大的工具。

1 贝叶斯网络的定义1.1贝叶斯网络的定义贝叶斯网络是由网络节点和连接网络节点的带方向的边构成的有向无环图，或者说是一种数据结构。

网络中的每个节点都表示一个变量，并且每个变量对应一个条件概率表，整个贝叶斯网络和其中的变量的条件概率表将变量的联合概率分布进行分解表示。

所以贝叶斯网络用于表示变量之间的依赖关系，并为联合概率分布提供了一种简明的规范。

其详细描述如下：1）其所有网络节点构成一个随机变量集。

变量可以是离散的或连续的。

2）其连接网络节点的是有向边或箭头。

如果存在从节点X指向Y的有向边，则称X是Y 的一个父节点。

3）其每个节点V i都有一个条件概率分布P(V i|Parents(V i))，量化其父节点对该节点的影响，就是给出在父节点的条件下当前节点各种状态的出现概率。

4）图中不存在有向环，因此是一个有向无环图，简写为DAG;1.2贝叶斯网络的一些例子例1 汽车诊断的部分贝叶斯网络图1：对汽车不能启动进行诊断的贝叶斯网络（先验概率）当任何变量的状态已知时，可将其作为证据输入，并对网络概率进行更新图2：输入证据汽车启动=false(100%)的贝叶斯网络进行概率更新（后验概率）图2在已知汽车不能正常工作的情况下，可以看出导致该结果的最大可能原因是火花塞（spark plugs=ok(45%), battery voltage=strong(80%)）。

图3输入证据汽车启动=false(100%) 前灯=off(100%)的网络概率更新（后验概率） 图3是在输入证据汽车启动=false (100%)的基础上一个好的诊断系统可能推荐测试车前灯，如果车前灯不能正常工作，前灯=off (100%)也作为证据输入，并对网络进行更新，battery voltage=none(53%),火花塞电压=ok=62.6，可以推断是电池电压不正常。