正午、午夜太阳高度角

夏至日各时段太阳高度角及太阳方位角太阳高度角还是太阳方位角，都跟纬度有关，不确定所在地计算出来的结果都会大大不同。

夏至日太阳到达北回归线上，在北回归线上，太阳高度角在正午（12:00）是九十度。

但是随着纬度的增加，太阳高度角越来越小。

在北极点而上，太阳高度角是0,也就是说在地平线上。

北半球的其他地点，其各时段的太阳高度角从日出时分的0°，到正午时分的最大角度，再到日落时的0度。

太阳高度角在0°到（所在地的维度-23°26′）之间变化。

太阳高度角简称为“太阳高度”(其实是角度)。

太阳高度是决定地球表面获得太阳热能数量的最重要的因素。

我们用h来表示这个角度，它在数值上等于太阳在地球地平坐标系中的地平高度。

一般时间太阳高度角随着地方时和太阳的赤纬的变化而变化。

太阳赤纬（与太阳直射点纬度相等）以δ表示，观测地地理纬度用φ表示（太阳赤纬与地理纬度都是北纬为正，南纬为负），地方时(时角)以t表示，有太阳高度角的计算公式：sinh=sinφsinδ+cosφcosδcost太阳高度是赤道冬至日的太阳高度为:90°-[0°-(-23.5°)]=113.5°太阳绕银河系中心公转，绕银河系中心公转周期约2.5×10⁸年。

银河系中心可能有巨大黑洞，但它周围布满了恒星，所以看上去象"银盘"。

这些恒星都绕"银核"公转。

与地球公转不同，这些恒星公转每绕一周离"银核"会更近。

根据太阳活动的相对强弱，太阳可分为宁静太阳和活动太阳两大类。

宁静太阳是一个理论上假定宁静的球对称热气体球，其性质只随半径而变，而且在任一球层中都是均匀的，其目的在于研究太阳的总体结构和一般性质。

在这种假定下，按照由里往外的顺序，太阳是由核心、辐射区、对流层、光球层、色球层、日冕层构成。

光球层之下称为太阳内部;光球层之上称为太阳大气。

午夜和正午太阳高度的判读近年来，在地理高考和各种模考中经常出现午夜太阳高度和正午太阳高度的计算问题，如"立竿见影"测当地地理坐标、合理楼距的计算、太阳热水器的安装、室内采光、影子长度的计算等等。

正午太阳高度角计算公式H=90°-|φ+δ|结合地方时换算已为大家所熟知，但是许多学生却对此公式应用的灵活性掌握不好，导致错误较多，究其原因，是缺少自己亲自动手进行推导所致。

以下步骤可以引导大家进行简单的数学推理：假设P点是北半球北纬φ度纬线上的一点，则当太阳直射点在北半球北纬δ度（0<δ≤23°26’）纬线上时（如图1）解直角三角形很容易得出H=90°-|φ-δ|；而当太阳直射点在南半球南纬δ度（0<δ≤23°26’）纬线上时（如图2）解直角三角形很容易得出H=90°-|φ＋δ|当太阳直射点在赤道时（如图3）解直角三角形很容易得出H=90°-φ因此，正午太阳高度角计算常被老师总结为：H=90°-|纬度差|①已知点与太阳直射点在赤道同侧时（即该点夏半年），纬差为已知点与直射点之差的绝对值：H=90°-|φ-δ|②已知点与太阳直射点在赤道两侧时（即该点冬半年），纬差为已知点与直射点之和的绝对值：H=90°-|φ+δ|③当太阳直射点在赤道上时（即春秋分日时），纬差为已知点的纬度：H=90°-φ通过上面的分析，应该有所理解。

下来我们来回归主题：午夜太阳高度，即0点太阳高度了；正午太阳高度，即12点太阳高度，只有在极昼圈及其以内才会有午夜太阳高度。

那么午夜太阳高度、正午太阳高度以及太阳直射点的纬度之间有什么样的关系呢？首先，我们必须了解太阳高度这个概念，对于大多数学生而言，感觉很简单，其实只是死记硬背了一些知识，而并不懂相关的原理。

太阳高度角是太阳光线与地平面的夹角，在日期一定的情况下，太阳直射点是固定的，所以太阳光方向不变（如上图所示），但是随着纬度的变化，不同纬度地平面并不相同，所以引起高度角的变化，这也就是课本上总结出的正午太阳高度随纬度的变化规律:从直射点向南北两侧递减。

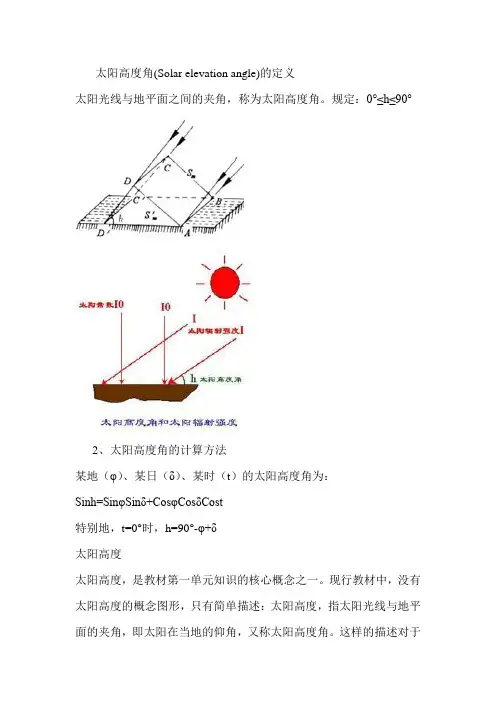
太阳高度角(Solar elevation angle)的定义太阳光线与地平面之间的夹角，称为太阳高度角。

规定：0°≤h≤90°2、太阳高度角的计算方法某地（φ）、某日（δ）、某时（t）的太阳高度角为：Sinh=SinφSinδ+CosφCosδCost特别地，t=0°时，h=90°-φ+δ太阳高度太阳高度，是教材第一单元知识的核心概念之一。

现行教材中，没有太阳高度的概念图形，只有简单描述：太阳高度，指太阳光线与地平面的夹角，即太阳在当地的仰角，又称太阳高度角。

这样的描述对于学生是抽象的。

在日常生活中，学生有太阳高度及其变化的直观感受，但并没有形成概念，如何使学生把日常观察到的熟悉现象，从感性认识提升到形成概念，是学习正午太阳高度纬度分布与季节变化规律首先要解决的问题。

在课堂学习正午太阳高度的变化一节知识前，布置学生观测课前某日8时、10时、12时、14时、16时的太阳高度。

让学生主动去思考“什么是太阳高度”、“怎样测量太阳高度”，激发学生主动探究地理问题的热情和兴趣。

在“立杆测影”的观测活动中，感受“太阳光线”、感悟“太阳高度”的概念，形成图2所示的太阳高度的“概念图像”。

图2 太阳高度，指太阳光线与地平面的夹角，即太阳在当地的仰角，又称太阳高度角这种概念图形及构建的思想方法，可以解决许多实际问题，如分析关于不同纬度热水器集热板的倾角大小及季节变化；在建筑楼房时，为了保证后楼一楼常年得到充足的光照，两楼的距离等问题。

详析太阳高度角知识江苏/王晨光一、太阳高度角与正午太阳高度角的概念太阳高度角是我们观察太阳时的仰角，也就是太阳光线与地面之间的夹角（如图1所示）。

由于地球的自转，造成太阳东升西落，太阳高度角在一日内不断发生变化（如图2所示）；正午（地方时为12时）太阳位于上中天时，太阳的高度角达到最大值H，我们将此时的太阳高度角称为该日的正午太阳高度角。

二、（正午）太阳高度角的时空分布规律1. 太阳高度角的分布规律（1）某时刻的空间分布如下图所示，此时刻太阳直射点A的太阳高度角为90°，从直射点向四周，随着球面的弯曲，太阳高度角递减，呈同心圆状分布，晨昏线上的太阳高度角为0°。

一年中正午太阳高度角的变化规律和影子正午太阳高度角是指太阳在正午时刻的高度与地平线的夹角。

太阳高度角的变化规律与影子息息相关。

下面将详细介绍太阳高度角的变化规律和与之相关的影子现象。

正午太阳高度角的变化规律是由地球自转和公转引起的。

地球自转是指地球绕自身轴线旋转一周所需要的时间，约为24小时。

而地球公转是指地球绕太阳运行一周所需要的时间，约为365.25天。

由于地球轴线与地球公转轨道平面有倾斜角度，使得太阳在不同季节和不同地点的高度角发生变化。

在北半球，夏至时太阳高度角最高，冬至时太阳高度角最低。

夏至时，太阳直射点位于北回归线上，此时北半球阳光照射时间长，太阳高度角最高，正午太阳直射点到地球表面的垂直角度最大。

冬至时，太阳直射点位于南回归线上，此时北半球阳光照射时间短，太阳高度角最低，正午太阳直射点到地球表面的垂直角度最小。

在赤道附近的热带地区，太阳高度角变化不大，因为直射点位于赤道附近，阳光照射角度较大，正午太阳高度角相对较高。

而在极地地区，夏季时太阳高度角很低，甚至太阳不曾落山，形成极昼现象；冬季时太阳高度角更低，太阳在地平线以下，形成极夜现象。

太阳高度角的变化对影子的形成和长度有直接影响。

当太阳高度角较高时，物体投射的影子较短；当太阳高度角较低时，物体投射的影子较长。

这是因为太阳光照射到物体上时，由于太阳光线的入射角度不同，形成的影子长度也不同。

太阳高度角的变化导致影子在一天中的长度发生变化。

在正午时刻，太阳的高度角达到最大值，此时物体投射的影子最短。

当太阳高度角较低时，物体投射的影子较长。

这一现象在日常生活中经常可以观察到。

例如，当太阳升起时，由于太阳高度角较低，人们的影子很长；而当太阳逐渐升高至正午时，人们的影子逐渐变短；当太阳开始下山时，人们的影子再次变长。

影子的长度还受到物体的高度和太阳的位置的影响。

当物体高度较低时，影子较长；当物体高度较高时，影子较短。

当太阳位于东方时，物体的西侧投射出较长的影子；当太阳位于西方时，物体的东侧投射出较长的影子。