波动光学一答案

第一章 波动光学通论 作业1、已知波函数为：⎪⎭⎫ ⎝⎛⨯-⨯=-t x t x E 157105.11022cos 10),(π，试确定其速率、波长和频率。

2、有一张0=t 时波的照片，表示其波形的数学表达式为⎪⎭⎫⎝⎛=25sin 5)0,(x x E π。

如果这列波沿负x 方向以2m/s 速率运动，试写出s t 4=时的扰动的表达式。

3、一列正弦波当0=t 时在0=x 处具有最大值，问其初位相为多少？4、确定平面波：⎪⎭⎫⎝⎛-++=t z ky k x kA t z y x E ω14314214sin ),,,(的传播方向。

5、在空间的任一给定点，正弦波的相位随时间的变化率为s rad /101214⨯π，而在任一给定时刻，相位随距离x 的变化是m rad /1046⨯π。

若初位相是3π，振幅是10且波沿正x 方向前进，写出波函数的表达式。

它的速率是多少？6、两个振动面相同且沿正x 方向传播的单色波可表示为：)](sin[1x x k t a E ∆+-=ω，]sin[2kx t a E -=ω，试证明合成波的表达式可写为⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∆+-⎪⎭⎫ ⎝⎛∆=2sin 2cos 2x x k t x k a E ω。

7、已知光驻波的电场为t kzcoa a t z E x ωsin 2),(=，试导出磁场),(t z B 的表达式，并汇出该驻波的示意图。

8、有一束沿z 方向传播的椭圆偏振光可以表示为)4cos()cos(),(00πωω--+-=kz t A y kz t A x t z E试求出偏椭圆的取向和它的长半轴与短半轴的大小。

9、一束自然光在30o 角下入射到空气—玻璃界面，玻璃的折射率n=，试求出反射光的偏振度。

10、过一理想偏振片观察部分偏振光，当偏振片从最大光强方位转过300时，光强变为原来的5／8，求 (1)此部分偏振光中线偏振光与自然光强度之比； (2)入射光的偏振度；(3)旋转偏振片时最小透射光强与最大透射光强之比； (4)当偏振片从最大光强方位转过300时的透射光强与最大光强之比．11、一个线偏振光束其E 场的垂直于入射面，此光束在空气中以45o 照射到空气玻璃分界面上。

第18单元 波动光学（一）学号 姓名 专业、班级 课程班序号一 选择题[ A ]1. 如图所示，折射率为2n 、厚度为e 的透明介质薄膜的上方和下方的透明介质折射率分别为1n 和3n ，已知321n n n <<。

若用波长为λ的单色平行光垂直入射到该薄膜上，则从薄膜上、下两表面反射的光束①与②的光程差是(A) 22n e (B) 2e n 2λ-21(C) 22n e λ- (D) 22n e 22n λ-[ A ]2. 双缝干涉的实验中，两缝间距为d ，双缝与屏幕之间的距离为D （D >>d ），单色光波长为λ，屏幕上相邻的明条纹之间的距离为 (A)dD λ (B) D d λ (C) d D 2λ (D) D d2λ[ B ]3. 如图，1S 、2S 是两个相干光源，它们到P 点的距离分别为 1r 和2r 。

路径1S P 垂直穿过一块厚度为1t 、折射率为1n 的介质板，路径P S 2垂直穿过厚度为2t 、折射率为2n 的另一块介质板，其余部分可看作真空，这两条路径的光程差等于 (A) )()(111222t n r t n r +-+(B) ])1([])1([111222t n r t n r -+--+ (C) )()(111222t n r t n r ---(D) 1122t n t n -[ C ]4. 如图所示，平行单色光垂直照射到薄膜上，经上下两表面反射的两束光发生干涉，若薄膜的厚度为e ，并且321n n n ><, 1λ 为入射光在折射率为n 1的媒质中的波长，则两束反射光在相遇点的相位差为(A) 1122λπn e n (B) πλπ+1212n en (C) πλπ+1124n e n (D) 1124λπn en 。

[ B ]5. 如图，用单色光垂直照射在观察牛顿环的装置上。

当平凸透镜垂直向上缓慢平移而远离平面玻璃时,可以观察到这些环状干涉条纹(A) 向右平移 (B) 向中心收缩 (C) 向外扩张 (D) 静止不动(E) 向左平移[ D ]6. 在迈克尔逊干涉仪的一支光路中，放入一片折射率为n 的透明介质薄膜后，测出两束光的光程差的改变量为一个波长?，则薄膜的厚度是 (A) 2λ (B) n 2λ (C) nλ(D) )1(2-n λ二 填空题1λe1n 2n 3单色光O.λe1n 2n 3①②S 1 S 21r 2r 1n 2n 1t 2tP1. 如图所示，两缝 1s 和 2s 之间的距离为d ，媒质的折射率为n =1，平行单色光斜入射到双缝上，入射角为θ，则屏幕上P 处，两相干光的光程差为21sin r r d θ--。

波动光学试题及答案1. 光波的波长为600nm，其频率是多少？答案：根据光速公式c = λν，其中c为光速（约为3×10^8m/s），λ为波长（600×10^-9 m），可得ν = c/λ = (3×10^8m/s) / (600×10^-9 m) = 5×10^14 Hz。

2. 一束光在折射率为1.5的介质中传播，其在真空中的速度是多少？答案：在折射率为1.5的介质中，光的速度v = c/n，其中c为真空中的光速（3×10^8 m/s），n为折射率。

因此，v = (3×10^8 m/s) / 1.5 = 2×10^8 m/s。

3. 光的偏振现象说明了什么？答案：光的偏振现象说明光是一种横波，即光波的振动方向与传播方向垂直。

4. 何为布儒斯特角？答案：布儒斯特角是指当光从一种介质（如空气）入射到另一种介质（如玻璃）时，反射光完全偏振时的入射角。

5. 干涉现象产生的条件是什么？答案：干涉现象产生的条件是两束光波的频率相同、相位差恒定且具有相同的振动方向。

6. 描述杨氏双缝干涉实验的基本原理。

答案：杨氏双缝干涉实验的基本原理是利用两个相干光源（如激光）通过两个相邻的狭缝产生两束相干光波，这两束光波在屏幕上相互叠加，形成明暗相间的干涉条纹。

7. 光的衍射现象说明了什么？答案：光的衍射现象说明光在遇到障碍物或通过狭缝时，其传播方向会发生改变，形成明暗相间的衍射图样。

8. 单缝衍射的中央亮条纹宽度与哪些因素有关？答案：单缝衍射的中央亮条纹宽度与光的波长、缝宽以及观察距离有关。

9. 光的色散现象是如何产生的？答案：光的色散现象是由于不同波长的光在介质中传播速度不同，导致折射率不同，从而在介质界面处发生不同程度的折射。

10. 描述光的全反射现象。

答案：光的全反射现象是指当光从光密介质（折射率较大）向光疏介质（折射率较小）传播时，如果入射角大于临界角，则光线不会折射，而是全部反射回光密介质中。

s 一.选择题[ B]1. 在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是(A) 使屏靠近双缝． (B) 使两缝的间距变小．(C) 把两个缝的宽度稍微调窄．(D) 改用波长较小的单色光源．参考解答：根据条纹间距公式，即可判断。

Dx ndλ∆=[B]2. 在双缝干涉实验中，入射光的波长为 ，用玻璃纸遮住双缝中的一个缝，若玻璃纸中光程比相同厚度的空气的光程大2.5 ，则屏上原来的明纹处 (A) 仍为明条纹； (B) 变为暗条纹；(C) 既非明纹也非暗纹； (D) 无法确定是明纹，还是暗纹参考解答：光程差变化了2.5 ，原光程差为半波长的偶数倍 形成明纹 ，先光程差为半波长的奇数倍，故变为暗条纹。

[A]3. 如图所示，波长为 的平行单色光垂直入射在折射率为n 2的薄膜上，经上下两个表面反射的两束光发生干涉．若薄膜厚度为e ，而且n 1＞n 2＞n 3，则两束反射光在相遇点的相位差为 (A) 4 n 2 e / ． (B) 2 n 2 e / ．(C) (4 n 2 e / ． (D) (2 n 2 e / ．参考解答：此题中无半波损失，故相位差为：。

22222e 4/n n e ππϕπλλλ∆=⨯⨯=光程差＝[B]4. 一束波长为 的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为 (A) ． (B) / (4n )．(C) ． (D) / (2n )．参考解答：反射光要干涉加强，其光程差应为半波长的偶数倍，故薄膜的最小厚度应满足如下关系式：(要考虑半波损失)，由此解得h 212nh λλ+=⋅ n 1λ。

/(4)h n λ= [C]5. 若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中，则干涉条纹 (A) 中心暗斑变成亮斑． (B) 变疏．(C) 变密． (D) 间距不变．参考解答：条纹间距，此题中变大，故条纹变密。

第一章 波动光学通论 作业1、已知波函数为：⎪⎭⎫ ⎝⎛⨯-⨯=-t x t x E 157105.11022cos 10),(π，试确定其速率、波长和频率。

2、有一张0=t 时波的照片，表示其波形的数学表达式为⎪⎭⎫⎝⎛=25sin 5)0,(x x E π。

如果这列波沿负x 方向以2m/s 速率运动，试写出s t 4=时的扰动的表达式。

3、一列正弦波当0=t 时在0=x 处具有最大值，问其初位相为多少？4、确定平面波：⎪⎭⎫⎝⎛-++=t z ky k x kA t z y x E ω14314214sin ),,,(的传播方向。

5、在空间的任一给定点，正弦波的相位随时间的变化率为s rad /101214⨯π，而在任一给定时刻，相位随距离x 的变化是m rad /1046⨯π。

若初位相是3π，振幅是10且波沿正x 方向前进，写出波函数的表达式。

它的速率是多少？6、两个振动面相同且沿正x 方向传播的单色波可表示为：)](sin[1x x k t a E ∆+-=ω，]sin[2kx t a E -=ω，试证明合成波的表达式可写为⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∆+-⎪⎭⎫ ⎝⎛∆=2sin 2cos 2x x k t x k a E ω。

7、已知光驻波的电场为t kzcoa a t z E x ωsin 2),(=，试导出磁场),(t z B 的表达式，并汇出该驻波的示意图。

8、有一束沿z 方向传播的椭圆偏振光可以表示为)4cos()cos(),(00πωω--+-=kz t A y kz t A x t z E试求出偏椭圆的取向和它的长半轴与短半轴的大小。

9、一束自然光在30o 角下入射到空气—玻璃界面，玻璃的折射率n=1.54，试求出反射光的偏振度。

10、过一理想偏振片观察部分偏振光，当偏振片从最大光强方位转过300时，光强变为原来的5／8，求 (1)此部分偏振光中线偏振光与自然光强度之比； (2)入射光的偏振度；(3)旋转偏振片时最小透射光强与最大透射光强之比； (4)当偏振片从最大光强方位转过300时的透射光强与最大光强之比．11、一个线偏振光束其E 场的垂直于入射面，此光束在空气中以45o 照射到空气玻璃分界面上。

第11章 波动光学一. 基本要求1. 解获得相干光的方法。

掌握光程的概念以及光程差与相位差的关系。

2. 能分析、确定杨氏双缝干涉条纹及等厚、等倾干涉条纹的特点（干涉加强、干涉减弱的条件及明、暗条纹的分布规律；了解迈克耳逊干涉仪的原理。

3. 了解惠更斯——菲涅耳原理；掌握分析单缝夫琅禾费衍射暗纹分布规律的方法。

4. 理解光栅衍射公式，会确定光栅衍射谱线的位置，会分析光栅常数及波长对光栅衍射谱线分布的影响。

5. 理解自然光和偏振光及偏振光的获得方法和检验方法。

6. 理解马吕斯定律和布儒斯特定律。

二. 内容提要1. 相干光及其获得方法 能产生干涉的光称为相干光。

产生光干涉的必要条件是：频率相同；振动方向相同；有恒定的相位差。

获得相干光的基本方法有两种：一种是分波阵面法（如杨氏双缝干涉、洛埃镜干涉、菲涅耳双面镜和菲涅耳双棱镜等）；另一种是分振幅法（如平行波膜干涉、劈尖干涉、牛顿环和迈克耳逊干涉仪等）。

2. 光程、光程差与相位差的关系 光波在某一介质中所经历的几何路程l 与介质对该光波的折射率n 的乘积n l 称为光波的光学路程，简称光程。

若光波先后通过几种介质，其总光程为各分段光程之和。

若在界面反射时有半波损失，则反射光的光程应加上或减去2λ。

来自同一点光源的两束相干光，经历不同的光程在某一点相遇，其相位差Δφ与光程差δ的关系为δλπϕ2=∆ 其中λ为光在真空中的波长。

3. 杨氏双缝干涉 经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况：一种是相位差为零或2π的整数倍，合成振幅最大—干涉加强；另一种是相位差为π的奇数倍，合成振动最弱或振幅为零——称干涉减弱或相消。

其对应的光程差为⎪⎩⎪⎨⎧=-±=±= 21k 212 210 干涉减弱），，（）（干涉加强），，（ΛΛλλδk k k 杨氏双缝干涉的光程差还可写成Dx d=δ ，式中d 为两缝间距离，x 为观察屏上纵轴坐标，D 为缝屏间距。

波动光学(1)波动光学试题1一、选择题：1、在双缝干涉实验中，若单色光源S到两缝S1、S2距离相等，则观察屏上中央明条纹位于图中O处．现将光源S向下移动到示意图中的S'位置，则(A)中央明条纹也向下移动，且条纹间距不变．(B)中央明条纹向上移动，且条纹间距不变．(C)中央明条纹向下移动，且条纹间距增大．(D)中央明条纹向上移动，且条纹间距增大．［］2、在双缝干涉实验中，设缝是水平的．若双缝所在的平板稍微向上平移，其它条件不变，则屏上的干涉条纹(A)向下平移，且间距不变．(B)向上平移，且间距不变．(C)不移动，但间距改变．(D)向上平移，且间距改变．［］3、在双缝干涉实验中，两缝间距离为d，双缝与屏幕之间的距离为D (D>>d)．波长为λ的平行单色光垂直照射到双缝上．屏幕上干涉条纹中相邻暗纹之间的距离是(A) 2λD / d．(B)λd / D．(C) dD /λ．(D)λD /d．［］4把双缝干涉实验装置放在折射率为n的水中，两缝间距离为d，双缝到屏的距离为D (D>>d)，所用单色光在真空中的波长为λ，则屏上干涉条纹中相邻的明纹之间的距离是(A)λD / (nd) (B) nλD/d．(C)λd / (nD)．(D)λD / (2nd)．［］5、一束波长为λ的单色光由空气垂直入射到折射率为n的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为(A)λ/ 4．(B)λ / (4n)．(C)λ/ 2．(D)λ / (2n)．［］6、在牛顿环实验装置中，曲率半径为R的平凸透镜与平玻璃扳在中心恰好接触，它们之间充满折射率为n的透明介质，垂直入射到牛顿环装置上的平行单色光在真空中的波长为λ，则反射光形成的干涉条纹中暗环半径r k的表达式为(A) r k=．(B) r k=．(C) r k=．(D) r k=．［］7、在迈克耳孙干涉仪的一条光路中，放入一折射率为n，厚度为d的透明薄片，放入后，这条光路的光程改变了(A) 2 ( n-1 ) d．(B) 2nd．(C) 2 ( n-1 ) d+λ / 2．(D) nd．(E) ( n-1 ) d．［］8、在迈克耳孙干涉仪的一支光路中，放入一片折射率为n的透明介质薄膜后，测出两束光的光程差的改变量为一个波长λ，则薄膜的厚度是(A)λ / 2．(B)λ / (2n)．(C)λ / n．(D) ．［］9、在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度为a＝4λ的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为(A) 2个．(B) 4个．(C) 6个．(D) 8个．［］10、一束波长为λ的平行单色光垂直入射到一单缝AB上，装置如图．在屏幕D上形成衍射图样，如果P是中央亮纹一侧第一个暗纹所在的位置，则的长度为(A)λ/ 2．(B)λ．(C) 3λ/ 2．(D) 2λ．［］二、填空题1、在双缝干涉实验中，若使两缝之间的距离增大，则屏幕上干涉条纹间距___________；若使单色光波长减小，则干涉条纹间距_________________．2、把双缝干涉实验装置放在折射率为n的媒质中，双缝到观察屏的距离为D，两缝之间的距离为d (d<<D)，入射光在真空中的波长为λ，则屏上干涉条纹中相邻明纹的间距是_______________________．3、在双缝干涉实验中，双缝间距为d，双缝到屏的距离为D (D>>d)，测得中央零级明纹与第五级明之间的距离为x，则入射光的波长为_________________．4、在双缝干涉实验中，若两缝的间距为所用光波波长的N倍，观察屏到双缝的距离为D，则屏上相邻明纹的间距为_______________．5、用λ＝600 nm的单色光垂直照射牛顿环装置时，从中央向外数第４个(不计中央暗斑)暗环对应的空气膜厚度为_______________________μm．(1 nm=10-9 m)6、在空气中有一劈形透明膜，其劈尖角θ＝1.0×10-4rad，在波长λ＝700 nm的单色光垂直照射下，测得两相邻干涉明条纹间距l＝0.25 cm，由此可知此透明材料的折射率n＝______________________．(1 nm=10-9 m)7、用波长为λ的单色光垂直照射折射率为n2的劈形膜(如图)图中各部分折射率的关系是n1＜n2＜n3．观察反射光的干涉条纹，从劈形膜顶开始向右数第5条暗条纹中心所对应的厚度e＝____________________．8、用波长为λ的单色光垂直照射如图所示的、折射率为n2的劈形膜(n1＞n2，n3＞n2)，观察反射光干涉．从劈形膜顶开始，第2条明条纹对应的膜厚度e＝___________________．9、用波长为λ的单色光垂直照射折射率为n的劈形膜形成等厚干涉条纹，若测得相邻明条纹的间距为l，则劈尖角θ＝_______________．10、用波长为λ的单色光垂直照射如图示的劈形膜(n1＞n2＞n3)，观察反射光干涉．从劈形膜尖顶开始算起，第2条明条纹中心所对应的膜厚度e＝___________________________．三、计算题：（每题10分）1、在双缝干涉实验中，所用单色光的波长为600 nm，双缝间距为1.2 mm双缝与屏相距500 mm，求相邻干涉明条纹的间距．2、在双缝干涉实验中，双缝与屏间的距离D＝1.2 m，双缝间距d＝0.45mm，若测得屏上干涉条纹相邻明条纹间距为1.5 mm，求光源发出的单色光的波长λ．3、用波长为500 nm (1 nm=10-9 m)的单色光垂直照射到由两块光学平玻璃构成的空气劈形膜上．在观察反射光的干涉现象中，距劈形膜棱边l= 1.56 cm的A处是从棱边算起的第四条暗条纹中心．(1)求此空气劈形膜的劈尖角θ；(2)改用600 nm的单色光垂直照射到此劈尖上仍观察反射光的干涉条纹，A处是明条纹还是暗条纹？(3)在第(2)问的情形从棱边到A处的范围内共有几条明纹？几条暗纹？4、一束自然光以起偏角i0＝48.09°自某透明液体入射到玻璃表面上，若玻璃的折射率为1.56，求：(1)该液体的折射率．(2)折射角．5、三个偏振片P-1、P-2、P-3顺序叠在一起，P-1、P-3的偏振化方向保持相互垂直，P-1与P-2的偏振化方向的夹角为α，P-2可以入射光线为轴转动．今以强度为I0的单色自然光垂直入射在偏振片上．不考虑偏振片对可透射分量的反射和吸收．(1)求穿过三个偏振片后的透射光强度I与α角的函数关系式；(2)试定性画出在P-2转动一周的过程中透射光强I随α角变化的函数曲线．大学物理------波动光学1参考答案一、选择题1-5BBDAB 6-10 BADBB二、填空题1.变小，变小；2. ；3. ；4. ；5.；6. ；7. ；8. ；9. ；10. ；三、计算题1、解：相邻明条纹间距为，代入a＝1.2 mm，λ＝6.0×10-4mm，D＝500 mm可得∆x＝0.25 mm。

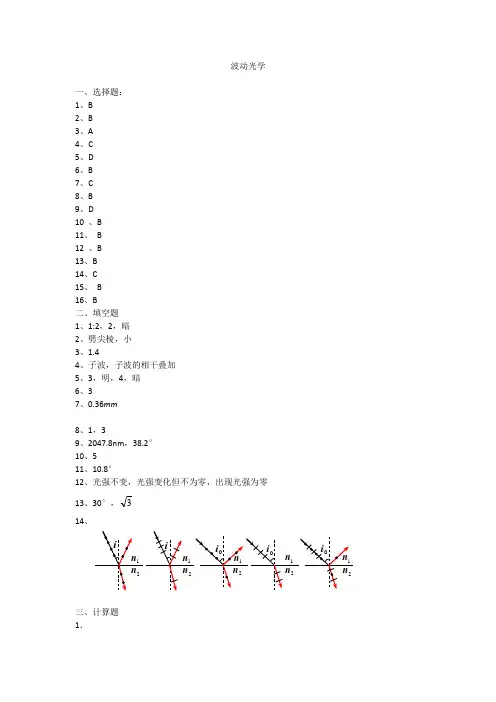
波动光学一、选择题：1、B2、B3、A4、C5、D6、B7、C8、B9、D10 、B11、 B12 、B13、B14、C15、 B16、B二、填空题1、1:2，2，暗2、劈尖棱，小3、1.44、子波，子波的相干叠加5、3，明，4，暗6、37、0.36mm8、1，39、2047.8nm ，38.2°10、511、10.8°12、光强不变，光强变化但不为零，出现光强为零13、30°，314、三、计算题1．解：设云母的厚度为l 。

有云母时，光程差为l n Dxd )1(--=δ x =0处的光程差为l n )1(-=δx =0处为第k =7级明纹时λδk l n =-=)1()(1064.6158.1105507169m n k l --⨯=-⨯⨯=-=λ2． 解：θλsin 2n l =5391088.3100.552.12103.5892sin ---⨯=⨯⨯⨯⨯==nl λθ，8''=θ3．解：中央明纹宽度：)(1046.51010.0100.5465.022233900m a D Dtg x ---⨯=⨯⨯⨯===λθ∆∆ 第二级明纹宽度：)(1073.23m a DDtg x -⨯===λθ∆∆4．解： 22sin 2)12(sin 2211λθλθk a k a =+= 472121221==+λλk k 21724k k =+即：2,321==k k5．解：2)122(2)12(sin 2)132(2)12(sin λλθλλθ+⨯=+='+⨯='+'=k a k a nm 6.4286007575=⨯=='λλ6．解：（1）λθk b a =+sin )(m k b a k 691062.01060002sin --⨯=⨯⨯==+θλ （2）λθk a '=sinλθk b a =+sin )(m k k b a a 66105.114106--⨯=⨯⨯='+= （3）λθk b a =+sin )(全部级数为。