OFDM符号调制解调

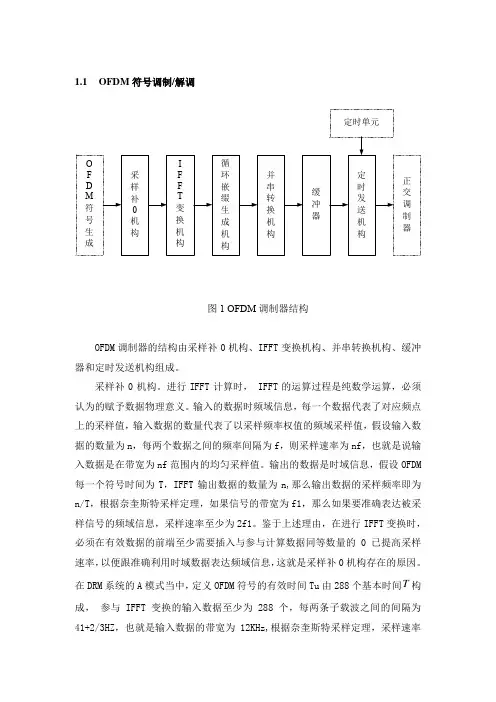
1.1OFDM符号调制/解调图1 OFDM调制器结构OFDM调制器的结构由采样补0机构、IFFT变换机构、并串转换机构、缓冲器和定时发送机构组成。

采样补0机构。

进行IFFT计算时， IFFT的运算过程是纯数学运算，必须认为的赋予数据物理意义。

输入的数据时频域信息，每一个数据代表了对应频点上的采样值，输入数据的数量代表了以采样频率权值的频域采样值，假设输入数据的数量为n，每两个数据之间的频率间隔为f，则采样速率为nf，也就是说输入数据是在带宽为nf范围内的均匀采样值。

输出的数据是时域信息，假设OFDM 每一个符号时间为T，IFFT输出数据的数量为n,那么输出数据的采样频率即为n/T，根据奈奎斯特采样定理，如果信号的带宽为f1，那么如果要准确表达被采样信号的频域信息，采样速率至少为2f1。

鉴于上述理由，在进行IFFT变换时，必须在有效数据的前端至少需要插入与参与计算数据同等数量的0已提高采样速率，以便跟准确利用时域数据表达频域信息，这就是采样补0机构存在的原因。

在DRM系统的A模式当中，定义OFDM符号的有效时间Tu由288个基本时间T构成，参与IFFT变换的输入数据至少为288个，每两条子载波之间的间隔为41+2/3HZ，也就是输入数据的带宽为12KHz,根据奈奎斯特采样定理，采样速率至少为24KHz，也就是参与运算的数据最少为576个，进而至少需要在288个有效数据之前插入288个0值。

值得注意的是，根据以上计算思路，可以认定DRM 广播系统标准中给出的载波数量，仅针对的是10Hz带宽的信号，对于4.5KHz、5kHz、9kHz、18kHz和20kHz需要重新考虑子载波的数量，即进行IFFT变换输入数据的数量。

IFFT变换机构。

IFFT变换机构的主要功能是将频域信息转化为对应的时域信息，该环节的理论基础相对充实，不再赘述，但需要明确的一点是输入数据的数量与输出数据的数量相同。

循环嵌缀生成机构。

循环前缀是OFDM技术中很有意思的一种技术，它的使用几乎消除了使用均衡器的必要。

HiNOC 系统中OFDM 调制/解调处理器的设计及VLSI 实现廖凯孙滨崔小欣北京大学信息科学技术学院微电子学研究院摘要：本文基于HINOC 系统要求设计实现了OFDM 调制和解调处理器。

该处理器主要由256点快速傅里叶变换/反变换FFT/IFFT 功能模块和增加/去除16点循环前缀模块组成。

核心模块256点FFT/IFFT 模块采用基-算法和22SDF(Single-path Delay Feedback)结构实现，具有良好的性能和可重复利用性。

关键词：OFDM ，调制与解调，FFT/IFFT ，基算法，SDF221、引言正交频分复用OFDM （Orthogonal Frequency Division Multiplexing ）是现代通信系统中广泛使用的调制技术。

HiNOC 采用OFDM 调制方式，单信道内包括256个子载波，子载波间隔为62.5KHz 。

为了抑制对于相邻信道的干扰，单信道频带两则的子载波作为空闲子载波，不传输信息。

零频处的子载波同样作为空闲子载波，不传输信息。

用于传输信息的有效子载波数目为210个，有效带宽为13.125MHz 。

子载波分布如图1所示。

图1.HiNOC 子载波定义有效数据符号s (k )按照下面公式对应到各个有效子载波上。

OFDM 频域信号X S (k )与s (k )的相互关系如公式（1）所示[1]：（1）s(k+105), 1k 105Xs(k)=s(k-150) , 151k 2550 , k=0 or 106k 150≤≤⎧⎪≤≤⎨⎪≤≤⎩根据HINOC 系统要求，本文设计实现了一款256点OFDM 调制与解调处理器，用于实现数据时、频域间转换的调制解调需求。

OFDM 处理器的核心功能是快速傅里叶变换/反变换FFT/IFFT （Fast Fourier Transform/Inverse Fast Fourier Transform ）。

对于调制，是对256个子载波上的数据进行IFFT 运算变换到时域，并且将时域数据最后16个点复制到该OFDM 符号前端作为时域保护间隔；对于解调，即对去除了16点OFDM 循环前缀后的256点数据进行FFT 运算变换到频域。

实验四OFDM调制解调仿真一、实验目的（1）了解OFDM调制解调的原理。

（2）学会用星座图分析系统性能。

二、实验内容（1）编写MATLAB程序，实现OFDM系统调制解调。

（2）绘制各步骤图形并分析系统特性。

三、实验代码1、主代码如下：clear all;close all;N=input('请输入码元数');SNR=input('请输入信噪比');xx=randint(1,4*N); %原序列figure(1),stem(xx,'.k'); %原序列图形title('原序列');B=0;for m=1:4:4*NA=xx(m)*8+xx(m+1)*4+xx(m+2)*2+xx(m+3);B=B+1;ee(B)=A;endfigure(2),stem(ee,'.b');title('化为0~15的码元');yy=star(ee,N);figure(3),plot(yy,'.r'); %映射后的星座图title('映射后的星座图');ff=ifft(yy,N); %傅里叶反变换N1=floor(N*1/4);N3=floor(N*3/4);N5=floor(N*5/4);figure(4),stem(ff,'.m');title('傅里叶反变换后');for j=1:N1 %加循环前缀ss(j)=ff(N3+j);endfor j=1:N %变成长度为N*5/4的序列ss(N1+j)=ff(j);endfigure(5),stem(ss,'.k'); %画出图形title('加N/4循环前后缀');%ss=wgn(1,N5,0,10,'dBW','complex');ss=awgn(ss,SNR); %加入噪声figure(6),stem(ss,'.m'); %加入噪声后的图形title('加入噪声后');zz=fft(ss((N1+1):N5),N); %傅里叶变换figure(7),plot(zz,'.b'); %画图title('傅里叶变换后');rr=istar(zz,N); %星座图纠错figure(8),plot(rr,'.r'); %画图title('纠错后的星座图');dd=decode(rr,N); %解码figure(9),stem(dd,'.m'); %画图title('星座图纠错并解码后');%bb=d2b(dd,N);bb=d2bb(dd,N); %转化为0/1比特流figure(10),stem(bb,'.b');title('转化为0/1比特流后');2、调用的函数：（1）星座图映射%星座图映射function yy=star(xx,N)B=[-3-3*i,-3-i,-1-3*i,-1-i,-3+3*i,-3+i,-1+3*i,-1+i,3-3*i,3-i,1-3*i,1-i,3+3*i,3+i,1+3*i, 1+i];for j=1:Nyy(j)=B(xx(j)+1);end（2）星座图逆映射%星座图逆映射function rr=istar(zz,N)for j=1:Nif(mod((floor(real(zz(j)))),2)==0)zz1(j)=ceil(real(zz(j)));else zz1(j)=floor(real(zz(j)));endif(mod((floor(imag(zz(j)))),2)==0)zz1(j)=zz1(j)+ceil(imag(zz(j)))*i;else zz1(j)=zz1(j)+floor(imag(zz(j)))*i;endrr(j)=zz1(j);end（3）十进制转二进制function bb=d2b(dd,N)%十进制转二进制for j=1:N*4bb(j)=;endfor j=1:4:N*4bb1=dec2bin(dd(floor(j/4)+1),4);for k=1:4bb(4*(j-1)+k)=bb1(k);endend（4）十进制转化为01比特流%十进制转化为01比特流function bb=d2bb(dd,N)for j=1:N*4bb(j)=1;endj=1;while(j<=N*4)N1=ceil(j/4)a4=mod(dd(N1),2);dd(N1)=floor(dd(N1)/2);a3=mod(dd(N1),2);dd(N1)=floor(dd(N1)/2);a2=mod(dd(N1),2);dd(N1)=floor(dd(N1)/2);a1=mod(dd(N1),2);bb(j)=a1;j=j+1;bb(j)=a2;j=j+1;bb(j)=a3;j=j+1;bb(j)=a4;j=j+1;end（5）星座图逆映射function yy=decode(rr,N)for j=1:Nswitch(rr(j))%星座图逆映射case -3-3*iyy(j)=0;case -3-iyy(j)=1;case -1-3*iyy(j)=2;case -1-iyy(j)=3;case -3+3*iyy(j)=4;case -3+iyy(j)=5;case -1+3*iyy(j)=6;case -1+iyy(j)=7;case 3-3*iyy(j)=8;case 3-iyy(j)=9;case 1-3*iyy(j)=10;case 1-iyy(j)=11;case 3+3*iyy(j)=12;case 3+iyy(j)=13;case 1+3*iyy(j)=14;case 1+iyy(j)=15;otherwise break;endend四、五、实验结果。

单载波调制和OFDM调制单载波的调制：单载波的调制就是采用一个信号载波传送所有的数据信号。

无线信道的多路径散射会造成相邻符号之间的干扰，就是我们常说的符号间干扰（ISI）。

如果这一信号使有用信号恶化，影响到射频信号的正确解调，那么有两种方法来解决：一种是在接收机端采用均衡器来消除ISI干扰，可以达到接近OFDM调制的误码率。

另一种是采用分集天线的方式可以有效地消除这种干扰，即采用两个不同方向的天线来进行接收。

对于3.5G的频段，在城市的覆盖区中，不同天线接收的信号必须将延迟均方根值速度限制在1us或者更少，尽量减少延迟速度大于10us的信号的比例。

对于这些延迟速度的值，本地时间均衡器提供一个简单的解决方法。

按照这种方式，单载波系统能够与OFDM调制方式提供相同的误码率。

时分单载波处理系统提供很大的灵活性，因为发射的数据包能被动态调整到恰当的长度，而最小数据包的长度上没有限制。

如果需要，很小长度的数据包都能够被处理，如短的确认信号等。

这种方式相对于以数据块交换的系统如OFDM有着更高的传输效率和更低传输延迟的优点。

单载波调制的其它关键优势：单载波避免了多载波系统的在各相位相同时的最大瞬时电功率与平均电功率的比值（PAPR）很大的问题，这样在设计中可以采用更经济高效的功率放大器，技术更成熟，系统的稳定性更高。

单载波系统对频率偏移和相位噪声要求相对于OFDM系统要低得多。

对于突发的点对多点的通信系统，单载波的调制方式能够使频率和时间同步设计变得更加简单，同时提高了系统的稳定性。

OFDM 调制：OFDM调制方式是一种多载波调制方式，这种方式将一个载波分为许多个带宽较窄的次载波，这些次载波相互正交，采用快速傅立叶变换将这些次载波信号进行编码。

次载波频分器将信号反转，使之正交，对于n个次载波，每一个次载波的符号速率被载波调制器分为整个符号速率的1/n，这使得调制后符号速率长于多经延迟从而减少符号间干扰（ISI）。

LTE⼊门篇-4：OFDMOFDM是LTE物理层最基础的技术。

MIMO、带宽⾃适应技术、动态资源调度技术都建⽴在OFDM技术之上得以实现。

LTE标准体系最基础、最复杂、最个性的地⽅是物理层。

1.OFDM正交频分复⽤技术，由多载波技术MCM（Multi-Carrier Modulation，多载波调制）发展⽽来，OFDM既属于调制技术，⼜属于复⽤技术。

采⽤快速傅⾥叶变换FFT可以很好地实现OFDM技术，在以前由于技术条件限制，实现傅⾥叶变换的设备难度⼤，直到DSP芯⽚技术发展，FFT技术实现设备成本降低，OFDM技术才⾛向⾼速数字移动通信领域。

⾸批应⽤OFDM技术的⽆线制式有WLAN、WiMax等。

1.1 OFDM和CDMA多址技术是任何⽆线制式的关键技术。

LTE标准制定时⾯临的两⼤选择是CDMA和OFDM。

不选择CDMA的原因如下：⾸先CDMA不适合宽带传输，CDMA相对于GSM不过是增加了系统容量，提⾼了系统抗⼲扰能⼒。

但CDMA在⼤带宽时，扩频实现困难，器件复杂度增加。

所以WCDMA不能把带宽从5MHz增加到20MHz或更⼤。

假如未来⽆线制式⽀持100MHz，CDMA缺点更⼤，但OFDM不存在这个问题。

其次CDMA属于⾼通专利，每年需要向其⽀付⾼额专利费⽤。

最后，从频谱效率上讲，在5MHz带宽时两者频谱效率差不多，在更⾼带宽时，OFDM的优势才逐渐体现。

使⽤CDMA⽆法满⾜LTE制定的带宽灵活配置、时延低、容量⼤、系统复杂度低的演进⽬标，OFDM是真正适⽤于宽度传输的技术。

LTE采⽤OFDM，空中接⼝的处理相对简单，有利于设计全新的物理层架构，有利于使⽤更⼤的带宽，有利于更⾼阶的MIMO技术实现，降低终端复杂性，⽅便实现LTE确定的演进⽬标。

1.2 OFDM本质OFDM本质上是⼀个频分复⽤系统。

FDM并不陌⽣，⽤收⾳机接收⼴播时，不同⼴播电台使⽤不同频率，经过带通滤波器的通带，把想要听的⼴播电台接收下来，如图所⽰。

利用IDFT/DFT实现OFDM调制解调原理分析于爽电子系MG1123068 2012-09-22摘要正交频分复用（OFDM）是多载波调制（MCM）技术的一种，其基本思想是在频域内将信道分成若干正交子信道，每个子信道使用并行传输的子载波进行调制。

要实现OFDM传输系统，一般需要振荡源和相应的带通滤波器组，系统结构复杂，体现不出多载波传输的优势。

但是经过理论分析，多载波传输系统的调制与解调都可以用离散傅里叶变换（Discrete Fourier Transform ,DFT）实现，而又由于DFT有著名的快速算法FFT（Fast Fourier Transform ,FFT），使得多载波传输系统实现起来大为简化。

本文通过分析OFDM调制解调基本原理，简要阐述了为何可以用IDFT/DFT来实现OFDM调制与解调。

1.1 OFDM调制基本原理从时域上看，OFDM是将一路高速数据流经过串/并转换变为N路速率较低的子数据流，用它们分别去调制N路子载波后再进行并行传输，每个子载波数据流的速率是原高速数据流的1/N，即符号周期扩大为原来的N倍，这样，就把一个宽带频率选择性信道划分成了N个窄带平坦衰落信道，有效的对抗了多径时延扩展，特别适合于高速无线数据传输。

OFDM选择时域相互正交的子载波，它们虽然在频域相互混叠，却仍能在接收端被分离出来。

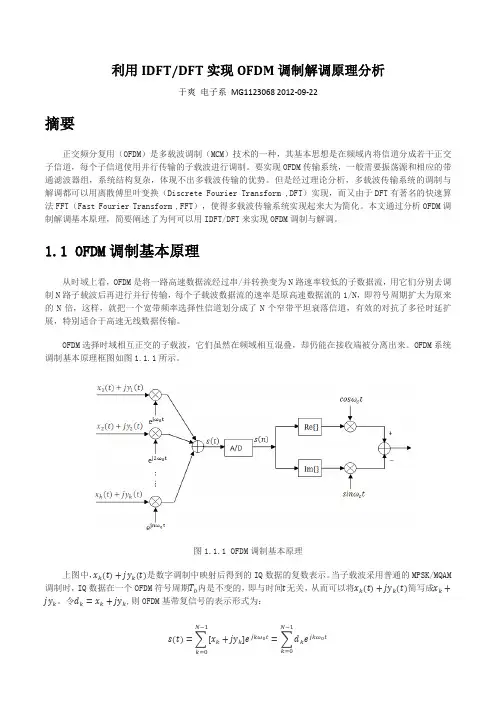
OFDM系统调制基本原理框图如图1.1.1所示。

图1.1.1 OFDM调制基本原理上图中，x k(t)+jy k(t)是数字调制中映射后得到的IQ数据的复数表示。

当子载波采用普通的MPSK/MQAM 调制时，IQ数据在一个OFDM符号周期T0内是不变的，即与时间t无关，从而可以将x k(t)+jy k t简写成x k+jy k。

令d k=x k+jy k,则OFDM基带复信号的表示形式为：s t=x k+jy k e jkω0tN−1k=0=d k e jkω0t N−1k=0为进行数字信号处理，对其进行采样，T0时间内采样N点，采样间隔为T0N。

OFDM课程实验报告课程名称:基于OFDM调制解调传输的通信系统.实验条件：MATLAB，SIMULINK实验设计思路：尽量保证各模块条理清晰，能很方便的从各子模块的名称中就可以很直观的理解该子模块是干什么用的，将同一个功能的元件打包封装成子系统，这样可以很方便的进行修改和以后的阅读。

第一章--------------前言，绪论OFDM的全称为Orthogonal Frequency Division Multiplexing，意为正交频分复用。

OFDM的思想可以追溯到20世纪60年代，当时人们对多载波调制做了许多理论上的工作，论证了在存在符号间干扰的带限信道上采用多载波调制可以优化系统的传输性能；1970年1月，有关OFDM的专利被首次公开发表；1971年，Weinstein和Ebert在IEEE杂志上发表了用离散傅里叶变换实现多载波调制的方法；20世纪80年代，人们对多载波调制在高速调制解调器、数字移动通信等领域中的应用进行了较为深入的研究，但是由于当时技术条件的限制，多载波调制没有得到广泛的应用；进入20世纪90年代，由于数字信号处理技术和大规模集成电路技术的进步，OFDM技术在高速数据传输领域受到了人们的广泛关注。

现在OFDM已经在欧洲的数字音视频广播（如DAB和DVB）、欧洲和北美的高速无线局域网系统（如HIPERLAN2、IEEE 802.11a）、高比特率数字用户线（如ADSL、VDSL）以及电力线载波通信（PLC）中得到了广泛的应用。

OFDM通信技术是多载波传输技术的典型代表。

多载波传输把数据流分解为若干个独立的子比特流，每个子数据流将具有低得多的比特速率，用这样低比特率形成的低速率多状态符号去调制相应的子载波，就构成了多个低速率符号并行发送的传输系统。

OFDM是多载波传输方案的实现方式之一，利用快速傅里叶逆变换（IFFT，Inverse Fast Fourier Transform）和快速傅里叶变换（FFT，Fast Fourier Transform）来分别实现调制和解调，是实现复杂度最低、应用最广的一种多载波传输方案。

The Research and the FPGA Realization ofOFDM Telecommunication ModemAbstractOrthogonal Frequency Division Multiplexing(OFDM) is a kind of digital modulation technology of multi-carriers which has many characteristics. It is suitable for the demand of the wireless telecommunications in high speed, broad band and mobility.This paper first describes the OFDM fundamental principle. For OFDM modulation, demodulation, characteristic and key technologies, it analyses them on theory and shows the more advantage than other modulating technology. Aim at channel estimation, deeply analyzes FFT-based cascade one-dimensional channel estimation algorithms and united iterative maximum likelihood semi-blind estimation algorithms, based on it, iterative maximum likelihood estimation algorithms is also described and compared by Matlab, both of them are validated.And then, OFDM system simulation platform is built with Matlab and Simulink. On this platform, the data curve is given for OFDM system based on various module parameter, just like multi-path fade, Gauss White noise and so on. Through analyzing the simulation result, some system performances can be appraised exactly.After combining the front several chapters and illuminating the OFDM system configuration and simulation analysis aimed to system characteristics, emphasis is design and implementation of OFDM baseband processing based on FPGA. According to802.16 protocol and OFDM characteristic, reasonable parameters are established. From modulator and demodulator to series-to-parallel conversion, QPSK mapping, sampling, pilot insertion, guard interval addition, IFFT/FFT and frame synchronization detection, paper makes design and implementation for every module of system, meanwhile present simulation waves and parameter explanation. Thereinto, due to limitation of fixed point, 24 float pointformat is design for system, and participated in IFFT/FFT with making full use of system resource and improving operation efficiency in parameter allowed. And IFFT/FFT based on FPGA is emphasized, for the problem that Algorithm operation time is excessively long and occupied resource is excessively more, new Algorithm with pipelining and less resource occupied is brought out and carried out. Putting it into OFDM baseband processing system, parameter is satisfied well. Afterward, based on OFDM theory, the system debugging and performance analysis is necessary to do and the feasibility of this design is proved.KEYWORDS:wirelessMAN, OFDM, FPGA, baseband processing, FFT/IFFTWritten by:Xia BinSupervised by:Lv JianpingOFDM通信系统调制解调器的研究及其FPGA实现第一章绪论第一章绪论随着以通信技术和计算机技术为标志的高科技的发展，人们的生活发生了日新月异的巨大变化。

1.OFDM调制/解调1.1. 概述1.1.1.OFDM调制基本原理如图OFDM调制的过程就是将待发送的多个数据分别与多路子载波相乘合成基带复信号s(t)的过程，而OFDM解调的过程就是由复信号s(t)求解傅立叶系数的过程。

复信号s(t)是时域信号，而傅立叶系数就是频域的数据。

需要明确的是：对于OFDM调制来讲，输入的数据是频域数据，而输出是S(t)就是时域数据；对于OFDM解调来讲，输入的s(t)是时域信号，而输出的数据就是频域数据。

当使用IDFT/DFT实现OFDM调制/解调的时候，IDFT 的输入是频域数据，输出是时域数据；DFT的输入是时域数据，输出是频域数据。

基于快速离散傅里叶变换的产生和接收OFDM信号原理：在发射端，输入速率为Rb 的二进制数据序列先进行串并变换，将串行数据转化成N个并行的数据并分配给N个不同的子信道，此时子信道信号传输速率为Rb/N。

N路数据经过编码映射成N个复数子符号Xk。

(一个复数子符号对应速率为Rb的一路数据)随后编码映射输出信号被送入一个进行快速傅里叶逆变换IFFT的模块，此模块将频域内N个复数子符号Xk变换成时域中2N个实数样值Xk。

（两个实数样值对应1个复数子符号，即对应速率为Rb的一路数据）由此原始数据就被OFDM按照频域数据进行处理。

计算出的IFFT变换之样值，被一个循环前缀加到样值前，形成一个循环扩展的OFDM信息码字。

此码字在此通过并串变换，然后按照串行方式通过D/A和低通滤波器输出基带信号，最后经过上变频输出OFDM信号。

1.1.2.OFDM的优缺点1.1.2.1. OFDM优点1.1.2.1.1.频谱效率高由于FFT处理使各个子载波可以部分重叠，因为理论上可以接近乃奎斯特极限。

以OFDM为基础的多址技术OFDMA（正交频分多址）可以实现小区内各用户之间的正交性，从而避免用户间干扰。

这使OFDM系统可以实现很高的小区容量。

1.1.2.1.2.带宽扩展性强由于OFDM系统的信号带宽取决于使用的子载波数量，因此OFDM系统具有很好的带宽扩展性。