[整理]matlab绘制二元函数图形.

表格一表格一数据整理ρ1为密度，ρ2为干密度，s为含沙量，w为含水量s= [0 0 0 0 0 0,20 20 20 20 20 20,40 40 40 40 40 40,60 60 60 60 60 60,70 70 70 70 70 70,80 80 80 80 100,100 100 100];w=[10 11.5 13.5 15 20 25,10 11.5 13.5 15 20 25,10 11.5 13.5 15 20 25,10 11.5 13.5 15 20 25,10 11.5 13.5 15 20 25,10 11.5 13.5 15 10,11.5 13.5 15];ρ1=[ 1.46 1.516 1.589 1.64 1.87 1.84,1.732 1.765 1.827 1.896 1.912 1.91,1.785 1.924 2.036 2.033 2.059 1.967,2.033 2.141 2.15 2.164 2.103 2.138,2.068 2.21 2.242 2.234 2.141 2.204,2.034 2.185 2.179 2.186 1.652,1.654 1.641 1.643]’; % 密度ρ2=[ 1.33 1.36 1.4 1.425 1.558 1.47,1.574 1.583 1.61 1.649 1.593 1.528,1.623 1.726 1.794 1.767 1.716 1.574,1.848 1.92 1.894 1.882 1.752 1.71,1.88 1.982 1.975 1.943 1.784 1.763,1.849 1.96 1.92 1.9 1.502,1.483 1.446 1.429]’; %干密度表格一模拟结果b1 = 0.98470.01880.0663-0.0002-0.0016stats1 =0.7597 26.0775 0.0000 0.0138b2 = 1.08260.01650.0417-0.0001-0.0014stats2 = 0.7391 23.3665 0.0000 0.0111故密度ρ1与含砂量S和含水率W的关系式回归模型为：221w 0016.0-s 0002.0w 0663.0s 0188.09847.0w)f(s,=-++=ρ 与F 对应的概率p=0.0138＜0.05，故而拒绝H 0，回归模型成立。

一、二维曲线的绘制
对于图形坐标的控制，请看图片自 己在上机实习的时候学会！
一、二维曲线的绘制
绘制函数的图形: 语法: fplot(‘fun’,lim,’s’):绘制函数fun的图形. 说明:fun为要绘制图形的函数,lim为图形的 范围,如:[0,2*pi],s为图形所用的点型,线 型和颜色的设定,与plot命令相同.
二、三维图形的绘制
2‘ 三维曲面图 语法：surf(z) surf(x,y,z) 说明：意义与mesh命令相同，只是图形不 是网线而是曲面。
三、特殊图形的绘制
1、条形图 语法：bar(x,y,width) %画条形图 bar3(x,y,width,’参数’) %画三维条形图 说明：x是横坐标向量，省略时默认值是1:m，m为y的向 量长度；y是纵坐标，当y是向量时，每个元素对应一 个竖条，当y是矩阵时，将画出m组竖条，每组包含n 条；width是竖条的宽度。默认时为0.8，（把bar命令 改为barh命令时将绘制出水平的条形图）。 三维的条形图中的参数可以detached, grouped,stacked三个,分别表示不同的显示方式.
一、二维曲线的绘制
数据点形 实点标记：. 圆圈标记：。 等等，其他更多的可以查相关的资料。 例如:>>x=0:0.1:2*pi; >>plot(x,sin(x),’r-.’) :用红色点划线 画出曲线 >>plot(x,cos(x),’b:*’)
一、二维曲线的绘制
6、交互式图形命令 （1）ginput命令 ginput命令与其他图形命令的原理不同， 不是把数据表现在图形上，而是从图上 获取数据。因此，ginput命令在数值优化、 工程设计中十分有用，仅适用于二维图 形。

1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8
24/32
绘网面命令mesh()使用格式: mesh(x,y,z) 或 mesh(z) 例1.12 绘二元函数 z = x exp( –x2 – y2)的图形。 [x,y]=meshgrid(-2:0.2:2); z=x.*exp(-x.^2-y.^2); mesh(x,y,z) colormap([0 0 1]) 注记: x,y是维数相同的矩阵; 表达式中“.*”和“.^”运算 使得z是与x,y维数相同矩阵。 功能相同的绘图命令:surf, meshc, meshz,· · · · · · · ·
11/32
三角函数与双曲函数
sin asin cos acos tan atan cot acot sec asec csc acsc 正弦函数 反正弦函数 余弦函数 反余弦函数 正切函数 反正切函数 余切函数 反余切函数 正割函数 反正割函数 余割函数 反余割函数 sinh asinh cosh acosh tanh atanh sech asech csch acsch coth acoth 双曲正弦函数 反双曲正弦函数 双曲余弦函数 反双曲余弦函数 双曲正切函数 反双曲正切函数 双曲正割函数 反双曲正割函数 双曲余割函数 反双曲余割函数 双曲余切函数 反双曲余切函数
1/3 1/4 1/5
19/32
————矩阵创建常用方法————
1.直接输入法; 2.特殊矩阵函数法; 3. 数据文件输入 注意事项 矩阵元素必须在方括号[ ]之内; 同一行相邻元素间用逗号或空格分隔; 矩阵的行与行之间用分号分隔. A=hilb(3) B=invhilb(3) A*B
掌握MATLAB程序设计方法
以MATLAB为操作平台完成实验作业

ans = 8 9
[i,j,v]=find(A) 返回矩阵A中非零元素所在的行i,
列j,和元素的值v(按所在位置先后 顺序输出)
A=[3 2 0; -5 0 7; 0 0 1]; [i,j,v]=find(A)
i= 1 2 1 2 3 j= 1 1 2 3 3 v = 3 -5 2 7 1
[X,Y]=meshgrid(x,y) 3)根据函数表达式生成全部网格节点出对应的函数值矩阵z： z＝f(X,Y) 4）顺序连接已经产生的空间点（x,y,z)绘制相应曲面： mesh（X,Y,Z) surf（X,Y,Z) shading flat ％去除网格线。
例2-7画出矩形域[-1,1]×[-1,1]旋转抛物面:z=x2+y2. x=linspace(-1,1,100); y=x; [X,Y]=meshgrid(x,y); %生成矩形区[-1,1]×[-1,1]的网格坐标矩阵 Z=X.^2+Y.^2; subplot(1,2,1) mesh(X,Y,Z); subplot(1,2,2) surf(X,Y,Z); shading flat; %对曲面z=x2现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
用matlab绘制二维、三维图形
2.1二维图形的绘制
2.1.1 二维绘图的基本命令 matlab中，最常用的二维绘图命令是plot。
使用该命令，软件将开辟一个图形窗口，并 画出连接坐标面上一系列点的连线。
例2-5 采用不同形式（直角坐标、参数、极坐标），画出 单位圆x2＋y2＝1的图形。
分析：对于直角坐标系方程，y＝ 1 x2，对于参数方 程x＝cost,y=sint,t[0,2 pi] ,利用plot(x,y)命令可以实现。 而在极坐标系中单位圆为r＝1(1+0t),利用polar(t,r)命 令实现。

实验一绘制二元熵函数曲线实验报告一、实验目的1.熟悉MATLAB工作环境及工具箱2.理解熵函数表达式及其性质二、实验内容用MATLAB软件编程绘制二元熵函数曲线三、实验过程1.复习二元熵函数，理解二元信源的熵H(w)=-wlogw-(1-w)log(1-w)表达式。

2.熟悉MATLAB软件。

1)MATLAB的操作界面MATLAB操作界面主要分为：任务栏、命令窗、命令历史窗、当前目录浏览器、工作空间浏览器及一个“启动按钮”。

任务栏：位于软件的正上方。

各个菜单分别为：文件、编辑、视窗、调试、桌面、窗体、帮助这几个窗口，点击每个窗口可以选择需要的操作。

命令窗(Command Window)：位于软件操作界面的右侧。

在此窗口里，可以输入各种指令、函数、变量表达式并进行各种操作。

该窗口用于输入命令并显示除图形以外的所有执行结果。

窗口中的“>>”为命令提示符，直接在其后面输入命令并按下回车键后，会出现计算结果在命令后面。

命令历史窗(Command History)：位于软件操作界面的左下方。

这个窗口记录了命令窗口已经运行过的所有命令（指令、函数等），允许用户对这些命令进行选择、复制。

2)MATLAB的函数绘制二维图形最常用的就是plot函数，调用plot函数的三种形式：plot(x)、plot(x,y)、plot(x,y,’r:x’)。

还有就是如何添加横坐标和纵坐标标题的命令语句。

3.实验程序。

w=0.000001:0.0001:0.999999999 %定义w的取值范围y=-w.*log2(w)-(1-w).*log2(1-w) %定义二元熵函数的表达式plot(w,y,'r') %画出二元熵函数的曲线图xlabel('w') %x轴的名称ylabel('H(w)') %y轴的名称grid on %给图形加上网格title('二元熵函数H(w)') %函数曲线的名称运行结果如下：四、实验结果分析从图中可以看出熵函数的一些性质，如果二元信源的输出概率是1或0（即二元信源的输出是确定的），则该信源不提供任何信息。

第二章绘图要画一个函数的图像，先是选取一堆x，求出相对应的y值，然后按照数值描点，接着用光滑的曲线把点连接起来。

和数学课讲的一样，在matlab中，我们画图也分为三步1. 建立一个x的点集；2. 根据函数关系式算出每个x对应y的点集；3. 将这些点用平滑的曲线连接起来。

例如要画y=sinx在[0,10]区间内的图像，首先我们要确定出x的区间>>x = [0:0.1:10];命令的意思是，产生一个数集，它从0开始，每次加0.1，一直加到10为止注意，命令后面的分号记得加上，否则matlab会把x的元素都打印出来，下面就是不加分号的后果：有了x的数集后，我们再根据函数关系式y=sinx得出y的点集>>y = sin(x);同样的，别忘了把分号加上抑制程序输出y的具体值，以及sin（x）的括号别忘了加到这里，我们已经把x和y确定下来，接下来只需用plot（x，y）命令即可绘制出图像>>plot(x,y)当然，如果你不定义y，而直接用一下嵌套命令也是可以的>>plot(x,sin(x))我们将x的增量变大一点，改为0到10，每次增幅为1，即>>x = [0:1:10];然后我们输入>>plot（x，y）我们会得到错误信息：原因是之前我们定义的y是由之前的x决定的，当x改变后，y依然没有改变，为了解决这个问题，我们要把y重新定义一遍，即命令要完整再输入一遍>>x = [0:1:10];>>y = sin(x);>>plot(x,y)然后程序会绘制出和我们预期相同的图像没错，我们将看到不光滑的曲线，这告诉我们，当使用plot（x，y）画图的时候x的增加幅度尽可能小一些，画出的图像才精确（跟数学里点越多图像越精确原理一样的）为了美化图像（有时是为了更清楚的辨析图像），我们经常要为图像加上网格，为坐标轴命名，改变曲线的颜色、形状这些命令2.1 加上网格我们使用grid on 命令我们这样书写：>>x=[0:0.1:10];y=sin(x);>>plot(x,y),grid on这样就画出了带网格的图像当然，也可以先画出没有网格的图像，再把窗口切回matlab命令输入窗口，输入grid on，这样图像就会加上网格，即>>x=[0:0.1:10];y=sin(x);>>plot(x,y)>>grid on2.2 为坐标轴命名为x坐标轴命名的命令是xlabel（），显然，y的就应该是ylabel（）比如这里，我想让x命名为x，y命名为sinx，则如下输入：>>x=[0:0.1:10];y=sin(x);>>plot(x,y)，xlabel（‘x’），ylabel（‘sinx’）注意，坐标轴的名字要用引号括起来，表示字符串当然也可以画图后再标坐标轴，即：>>x=[0:0.1:10];y=sin(x);>>plot(x,y)>>xlabel（‘x’）>>ylabel（‘sinx’）然后我们就可以看到坐标轴带命名的图像：2.3 绘制多条曲线绘制多条曲线有两种情况，一种是在同一个坐标面内画多条曲线，另一种是在一个面内画多个独立的曲线我们先讲第一种，假设我们要在一个坐标面内画sinx，cosx，tanx的图像先定义x，y>>x=[0:0.1:10]>>y1=sin(x);>>y2=cos(x);>>y3=tan(x);接着画图>>plot（x，y1）这时候函数绘制出了sinx的图像接着我们继续画>>plot（x，y2）我们会发现程序会把之前的sinx图像抹掉，然后绘制cosx的图像为了让他们同时存在，我们使用hold on命令，即画完一个图后，hold on，继续画当我们再加上tanx后会得到这个图像这是因为函数显示区间设置的原因，后面讲2.4 更改图像显示区间从楼上我们已经在一个图中画出了sinx、cosx、tanx的图像，但是我们知道tanx的值域是负无穷到正无穷，而sin，cos的值域是-1到1，这导致了我们基本上看不到sin，cos的图像，为了解决这个问题，我们只需用axis命令即可，命令格式为axis（[xmin xmax ymin ymax]）即括号内跟一个区间，四个数字分别是x的起点，x的终点，y的起点，y的终点。

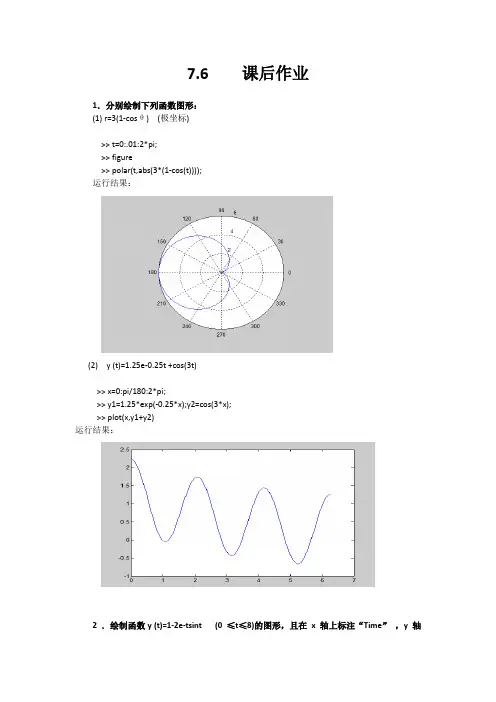
7.6 课后作业1．分别绘制下列函数图形：(1) r=3(1-cosθ) (极坐标)>> t=0:.01:2*pi;>> figure>> polar(t,abs(3*(1-cos(t))));运行结果：(2) y (t)=1.25e-0.25t +cos(3t)>> x=0:pi/180:2*pi;>> y1=1.25*exp(-0.25*x);y2=cos(3*x);>> plot(x,y1+y2)运行结果：2 ．绘制函数y (t)=1-2e-tsint (0 ≤t≤8)的图形，且在x 轴上标注“Time”，y 轴上标注“Amplitude”，图形的标题为“Decaying Oscillating Exponential”。

>> x=0:0.01:8;>> y=1-2*exp(-1*x).*sin(x);>> figure>> plot(x,y)>> xlabel('Time');ylabel('Amplitude');>> title('Decaying Oscillating Exponential');运行结果：3 ．在同一图中绘制下列两条曲线(x ∈[0,25]内) ：(1) y 1(t)=2.6e(-0.5x) cos(0.6x)+0.8 ；(2) y 2(t)=1.6cos(3x)+sin(x)要求用不同的颜色和线型分别表示y 1(t) 和y 2(t) ，并给图形加注解。

>> x=0:0.1:25;>> y1=2.6*exp(-0.5*x).*cos(0.6*x)+0.8;>> y2=1.6*cos(3*x)+sin(x);>> figure>> plot(x,y1,'r-X',x,y2,'b--.');>> legend('y1=2.6*exp(-0.5*x).*cos(0.6*x)+0.8','y2=1.6*cos(3*x)+sin(x)')4 ．在一个图形窗口下绘制两个子图，分别显示下列曲线：(1)y =sin2xcos3x ；(2) y =0.4 x要求给x 轴、y 轴加标注，每个子图加标题。

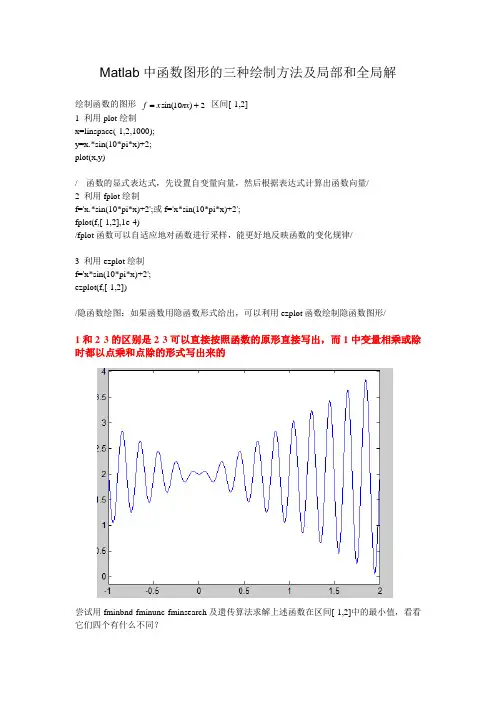
Matlab中函数图形的三种绘制方法及局部和全局解
绘制函数的图形2
x
fπ区间[-1,2]
=x
)
10
sin(+
1 利用plot绘制
x=linspace(-1,2,1000);
y=x.*sin(10*pi*x)+2;
plot(x,y)
/ 函数的显式表达式，先设置自变量向量，然后根据表达式计算出函数向量/
2 利用fplot绘制
f='x.*sin(10*pi*x)+2';或f='x*sin(10*pi*x)+2';
fplot(f,[-1,2],1e-4)
/fplot函数可以自适应地对函数进行采样，能更好地反映函数的变化规律/
3 利用ezplot绘制
f='x*sin(10*pi*x)+2';
ezplot(f,[-1,2])
/隐函数绘图：如果函数用隐函数形式给出，可以利用ezplot函数绘制隐函数图形/
1和2 3的区别是2 3可以直接按照函数的原形直接写出，而1中变量相乘或除时都以点乘和点除的形式写出来的
尝试用fminbnd fminunc fminsearch及遗传算法求解上述函数在区间[-1,2]中的最小值，看看它们四个有什么不同？。

MATLAB绘制二元函数的图形【实验目的】1.了解二元函数图形的绘制。

2.了解空间曲面等高线的绘制。

3.了解多元函数插值的方法。

4.学习、掌握MA TLAB软件有关的命令。

【实验内容】画出函数22y=的图形，并画出其等高线。

z+x【实验准备】1.曲线绘图的MA TLAB命令MA TLAB中主要用mesh,surf命令绘制二元函数图形。

主要命令mesh（x，y，z）画网格曲面，这里x，y，z是数据矩阵，分别表示数据点的横坐标，纵坐标和函数值，该命令将数据点在空间中描出，并连成网格。

surf（x，y，z）画完整曲面，这里x，y，z是数据矩阵，分别表示数据点的横坐标，纵坐标和函数值，该命令将数据点所表示曲面画出。

【实验重点】1. 二元函数图形的描点法2. 曲面交线的计算3. 地形图的生成【实验难点】1. 二元函数图形的描点法2. 曲面交线的计算【实验方法与步骤】练习1画出函数22y=的图形，其中]3,3xz+⨯-yx。

∈,[]3,3[(-)用MA TLAB作图的程序代码为>>clear;>>x=-3:0.1:3; %x的范围为[-3，3]>>y=-3:0.1:3; %y的范围为[-3，3]>>[X,Y]=meshgrid(x,y); %将向量x,y指定的区域转化为矩阵X,Y >>Z=sqrt(X.^2+Y.^2); %产生函数值Z>>mesh(X,Y,Z)运行结果为图5.3如果画等高线，用contour，contour3命令。

contour画二维等高线。

contour3画三维等高线。

画图5.3所示的三维等高线的MA TLAB 代码为>>clear;>>x=-3:0.1:3;>>y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);>>Z=sqrt(X.^2+Y.^2);>>contour3(X,Y,Z,10); %画10条等高线>>xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis'); %三个坐标轴的标记>>title('Contour3 of Surface') %标题>>grid on %画网格线运行结果为图5.4如果画图5.4所示的二维等高线，相应的MA TLAB代码为>>clear;x=-3:0.1:3;y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);Z=sqrt(X.^2+Y.^2);>>contour (X,Y,Z,10);>>xlabel('X-axis'),ylabel('Y-axis');>>title('Contour3 of Surface')>>grid on运行结果为如果要画z=1的等高线，相应的MATLAB代码为>>clear;x=-3:0.1:3;y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);Z=sqrt(X.^2+Y.^2);>>contour(X,Y,Z,[1 1])运行结果为练习2 二次曲面的方程如下222222x y z d a b c++= 讨论参数a ,b ,c 对其形状的影响。

18
【例6-4】 在图形中添加文本字符串。 x=0:0.1:10; y=sin(x); plot(x,y) xlabel('x') ylabel('y=sinx') text(0,sin(0),‘\leftarrowsin(x)=0’) % 在指定位置添
加左箭头及字符串
text(3*pi/4,sin(3*pi/4),'\rightarrowsin(x)=0.707') text(7*pi/4,sin(7*pi/4),'\leftarrowsin(x)=-0.707')
x=x+(x==0)*eps; % 用一个“机器0”小数代替0
y=sin(x)./x; % 用可逻辑运算的sin(esp)/esp近似代替sin(0)/0的极限
plot(x,y)
xlabel('x')
% 在x轴上标注x
ylabel('y=sinx/x')
% 在y轴上标注y=sinx/x
title('门函数的频谱') % 在图形上方添加标题
9
④plotyy指令的常用调用格式 plotyy(x1,y1,x2,y2) plotyy(x1,y1,x2,y2,'f') plotyy(x1,y1,x2,y2,'f1','f2')
指令中出现的参数f、f1、f2等代表绘制数据的 方式，可选择plot、semilogx、semilogy、 loglog等不同的形式。
28
⑤二维区域图的绘制 区域图的绘制使用area指令，该指令用于
在图形窗口中显示一段曲线，该曲线可由一 个矢量生成，也可由矩阵中的列生成(其实 在MATLAB中，矢量是矩阵的一种特殊形式 ，即列数为1的矩阵就是矢量)。如果矩阵的 列数大于1，则area指令将矩阵中每一列的 值都绘制为独立的曲线，并且对曲线之间和 曲线与x轴之间的区域进行填充。这种图形 在MATLAB中就称为区域图。

Matlab绘图函数⼀览 要查看Matlab所有绘图函数，请从Matlab主界⾯菜单查看“绘图⽬录”，或从Matlab帮助⽂档查看“Types of MATLAB Plots”（）。

本⽂的图和英⽂解释摘⾃Matlab帮助⽂档。

类别Function图维度描述曲线plot2绘制曲线，相邻点之间被插值fplot输⼊函数或函数句柄、⾃变量取值区间，绘制曲线plotyy2双纵坐标图，两个纵坐标的数量级不同plot33绘制3D曲线loglog2X,Y坐标都按对数缩放semilogx2仅X坐标按对数缩放semilogy2仅Y左边按对数缩放errorbar2误差条形图，见条形直⽅⾯域bar2条形图（垂直），分为grouped和stacked风格bar333D条形图（垂直）barh2⽔平条形图，分为grouped和stacked风格bar3h33D⽔平条形图hist2频数直⽅图histc输⼊数据和区间，返回数据落在每个区间的频数pareto2帕累托图（柏拉图），见area2填充区域图，曲线和X轴之间被填充pie2饼图，⽤于表⽰⽐例pie333D饼图极坐标polar2极坐标图，以极坐标绘制曲线rose2⾓直⽅图（频数扇形图）离散数据stem2杆图，对每个数据，从X轴伸出⼀条垂直线，顶端画圆圈stem333D杆图stairs2阶梯图，相邻点间不进⾏插值scatter2散点图（⽓泡图），绘制⼀系列散点scatter333D散点图spy2稀疏模式（sparsity pattern）图，对矩阵⾮0的地⽅绘制散点plotmatrix2将矩阵绘制为散点图或散点图和直⽅图等⾼线contour2等⾼线图，⼆维函数的等值线contour333D等⾼线图，三维函数（空间函数）的等值线contourf2填充的等⾼线图contourf2填充的等⾼线图contourc等⾼线计算曲⾯⽹格surf3曲⾯图，和mesh的区别是，surf在⼩矩形上做颜⾊插值surfl3在surf基础上，加⼊光照surfc3在surf基础上，在底部绘制等⾼线图surfnorm3在surf基础上，每个⾯绘制法线surface低层次曲⾯绘制函数mesh3⽹格图，在⾏和列上绘制⼀系列曲线，构成⽹格meshc3在mesh基础上，在底部绘制等⾼线图meshz3在mesh基础上，在⽹格四周绘制“帘⼦”waterfall3瀑布图，类似于meshz函数，但在矩阵的列之间不⽣成线ribbon3带图，绘制⼀定宽度的带，相当于将⼆维曲线沿着垂直平⾯⽅向拉开⼀定宽度形成三维图形pcolor2伪彩图，根据矩阵的“相邻四个点”的值对应颜⾊插值得到⼩矩形颜⾊peaks Example function of two variablescylinder Generate cylinderellipsoid Generate ellipsoidsphere Generate spheresurf2patch Convert surface data to patch data标量场体数据slice3体积切⽚图，对体数据进⾏切⽚观察contour-slice3切⽚等⾼线图，体数据在切⽚平⾯中的等值线flow Simple function of three variables isosurface Extract isosurface data from volume data isocaps Compute isosurface end-cap geometry isocolors Calculate isosurface and patch colors isonormals Compute normals of isosurface verticesreduce-patchReduce number of patch facesreduce-volume Reduce number of elements in volume data set shrinkfaces Reduce size of patch facessmooth3Smooth 3-D datasubvolume Extract subset of volume data setvolumeboundsCoordinate and color limits for volume data feather2⽻状图，以X轴上的点为起点绘制⼀系列向量向量场体向量数据compass2射线图，以原点为起点绘制⼀系列向量quiver2⽮量场图，以采样点为起点绘制⼀系列向量quiver333D⽮量场图streamslice3绘制流场（三维向量函数）在切⽚平⾯中的流线streamline3绘制流场的流线（类似于磁感线），起点由数据指定coneplot3绘制三维圆锥，圆锥的起点由数据指定，⽅向和⼤⼩由流场指定stream-particles3绘制流场marker粒⼦stream-ribbon3绘制流场ribbon图streamtube3绘制流场流管curl Compute curl and angular velocity of vector field divergence Compute divergence of vector fieldinterp-stream-speedInterpolate stream-line vertices from flow speedstream2Compute 2-D streamline datastream3Compute 3-D streamline data多边形fill2绘制填充的多边形fill333D填充多边形patch2,3绘制⼀个或多个填充多边形Easy-to-use ezplot2Easy-to-use版绘图函数，这类函数传⼊要绘制的函数或函数句柄，以及⾃变量的定义域，调⽤具体函数绘图。

一、介绍Matlab是一款用于科学计算和技术计算的软件，拥有强大的绘图功能，可以用于绘制各种图形、曲线和函数图像。

在Matlab中，使用plot函数可以绘制二元函数的图像，通过调整参数和设置属性，可以实现不同风格和效果的图像展示。

本文将详细介绍在Matlab中如何绘制二元函数的图像，包括基本的绘图方法和常用的设置技巧。

二、绘制二元函数图像的基本方法1. 准备数据在使用Matlab绘制二元函数的图像前，首先需要准备数据。

通常可以通过生成x、y坐标的网格点，然后计算每个点对应的函数值，从而得到二元函数在指定区域内的数据集。

2. 使用plot函数一旦准备好了数据集，就可以使用Matlab的plot函数进行绘图。

plot函数的基本语法为：plot(x, y)，其中x和y分别代表要绘制的点的横坐标和纵坐标。

通过调用plot函数，可以将计算得到的数据点连接起来，形成二元函数的图像。

3. 添加标签和标题为了让图像更加清晰和直观，通常需要添加x和y轴的标签，以及整个图像的标题。

在Matlab中，可以使用xlabel、ylabel和title函数来分别添加x轴、y轴和标题标签。

4. 设置图像属性通过设置图像的属性，可以调整图像的风格和效果。

常用的属性包括线型、线宽、颜色和标记符号等。

在Matlab中，可以使用参数-字符串对的形式来设置图像的属性，例如'LineStyle'、'LineWidth'、'Color'和'Marker'等。

三、绘制常见二元函数的图像在Matlab中，可以绘制各种类型的二元函数的图像，包括线性函数、二次函数、三角函数、指数函数、对数函数等。

下面将分别介绍如何绘制这些常见二元函数的图像。

1. 绘制线性函数图像线性函数的一般形式为y=ax+b，其中a和b分别为常数。

在Matlab 中，可以通过设置a和b的值，然后使用plot函数绘制线性函数的图像。

4．图形的标注 图名标注title title(‘String’) 在图形的顶端加注文字作为图名 坐标轴标注xlabel,ylabel,zlabel xlabel(‘String’) 在当前图形的x轴旁边加入文字内容 ylabel(‘String’) 在当前图形的y轴旁边加入文字内容 zlabel(‘String’) 在当前图形的z轴旁边加入文字内容
绘制三维图形时生 成空间曲面的格点。
等价于
[X,Y,Z]=meshgrid(x,x,x)
等价于
说明： x是区间[x0,xm]上分划点组成的m维向量； y是区间[y0,yn]上分划点组成的n维向量； 输出变量X与Y都是n×m矩阵； 矩阵X的行向量都是向量x； 矩阵Y的列向量都是向量y。
legend作用是：对图形进行图例标注
例2的绘图结果
图形的重叠绘制hold hold 在hold on与 hold off之间进行切换 hold on 保留当前图形和它的轴,使此后图形叠放在当前图形上 hold off返回Matlab的缺省状态。此后图形指令运作将抹掉当前窗中的旧图形，然后画上新图形。
说明：2、当x为n维向量,y为n * m矩阵时，plot(x,y) 按向量x分别与矩阵y的每一列匹配，画出m条曲线或折线。
例 x=[ 3 4 7]; y=[4 5 6 5 4 7 9 5 1 4 2 5]; plot (x,y)
可以。 x=a:h:b 函数f(x)在绘图区间[a,b]上的自变量点向 量数据 y=f(x) 对应的函数值向量 步长h可以任意选取，步长越小，曲线越光滑。
meshgrid的调用形式是：
[X,Y]=meshgrid(x,y)
[X,Y]=meshgrid(x)
[X,Y,Z]=meshgrid(x,y,z)

图4-4 图4-5 数学实验四 用Matlab 软件作二元函数的图象一、空间曲线调用格式：plot3(x1,y1,z1,x2,y2,z2,…,xn,yn,zn)其中xi 、yi 和zi 为分别是长度相同的向量，用于存储xi 坐标、yi 坐标和zi 坐标数据，i=1,2,…,n ．例1 在同一坐标系中分别作出三维曲线 ==x x z x x y cos sin 和+=−=2442x z x y 在]6,0[π∈x 上的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：x=0:pi/50:6*pi;y1=x.*sin(x);z1=x.*cos(x);y2=2*x-1;z2=4*x-8;plot3(x,y1,z1,x,y2,z2);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')legend('圆锥螺线','空间直线')取名为exa1保存，再在命令窗口中输入命令exa1，程序运行结果如图4-4．说明：若要作单根曲线，和前面plot 函数一样，只是多了一个立坐标．二、空间曲面1．三维网格图调用格式一：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)plot3(x,y,z)其中x 、y 和z 为长度相同的向量，分别用于存储x 坐标、y 坐标和z 坐标数据． 例2 作出空间平面324=+−z y x 的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-3:0.1:3,-2:0.1:3); %产生一个x,y 平面上51×61的网格z=3-4*x+2*y;plot3(x,y ,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')title('4x-2y+z=3')取名为exa2保存，再在命令窗口中输入命令exa2，程序运行结果如图4-5．例3 作出空间曲面2222sin y x y x z ++=在区域图4-7图4-8}8||,8|||),{(≤≤y x y x 上的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-8:0.1:8);r=sqrt(x.^2+y.^2); %产生对应的x,y 坐标用点幂z=sin(r)./r; %产生对应于x,y 的z 坐标用点除plot3(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa3保存，再在命令窗口中输入命令exa3，程序运行结果如图4-6．调用格式二：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)mesh(x,y,z)例4 在x 、y 平面内选取一个区域，作出空间曲面22y xe z −−=的图象． 解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-4:0.1:3,-3:.1:2); %产生一个x,y 平面上51×71的网格z=exp(-x.^2-y.^2);mesh(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa2保存，再在命令窗口中输入命令exa2，程序运行结果如图4-7．2．三维曲面图调用格式：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)surf(x,y,z) 说明：surf 函数可借助shading 函数作平滑和插值处理，而shading 函数有三个参数，分别为flat （作平滑处理）、interp （去掉连接线条，在各片之间使用颜色插值）和faceted （默认值，对前面两种参数之一的作用进行还原）．例5 用子图分别作出马鞍面22y x z −=在区域}2||,1|||),{(≤≤y x y x 图和经插值处理的图．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-1:0.1:1,-2:.1:2);z=x.^2-y.^2;subplot(1,2,1),surf(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')title('z=x^2-y^2');subplot(1,2,2),surf(x,y,z);图4-9 图4-10xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')shading interp %插值处理title('z=x^2-y^2的插值处理图')取名为exa5保存，再在命令窗口中输入命令exa5，程序运行结果如图4-8．3．柱面图调用格式一：[x,y,z]=cylinder(R,N)mesh(x,y,z)其中，R 是一个向量，其坐标分量依次对应柱面各横截面的半径，Ｎ是多边形的边数．默认值是Ｒ＝[1,1]，Ｎ＝20．例6 作出正六棱柱在Ｒ＝[２,２]的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y,z]=cylinder([2,2],6);mesh(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')hidden off %显示隐含线，若不想显示隐含线，则取消此命令或设置为hidden on取名为exa6保存，再在命令窗口中输入命令exa6，程序运行结果如图4-9． 调用格式二：[x,y,z]=cylinder(R,N)surf(x,y,z)其中，R 、Ｎ的意义和上面一样．例7 作出正十棱台在Ｒ＝[1,2]的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y,z]=cylinder([1,2],10);surf(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa7保存，再在命令窗口中输入命令exa7，程序运行结果如图4-10．说明：若要作正棱锥，只须取Ｒ的某个分量为0即可．4．球面图调用格式：[x,y,z]=sphere(N)surf(x,y,z) 其中，N （N>2）是球面的边数．默认值是Ｎ＝20．sphere(N)不返回坐标，直接绘出球面．例8 以子图形式分别作出N=5、20、40和40并作平滑处理的球．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：subplot(2,2,1)sphere(5);title('子图1')subplot(2,2,2),sphere;title('子图2')subplot(2,2,3)[x,y,z]=sphere(40);surf(x,y,z);title('子图3')subplot(2,2,4)[x,y,z]=sphere(40);surf(x,y,z);shading flat %对球面作平滑处理title('子图4') 取名为exa8保存，再在命令窗口中输入命令exa8，程序运行结果如图4-11．三、上机实验1．用help 命令查看函数plot3，mesh 和surf 等的用法．2．上机验证上面各例．3．作相关小节练习中空间曲线和曲面的图象．图4-11。

I. 隐函数f(x,y)=0, f(x(t),y(t),z(t))=0; z=f(x,y)ezplot, ezplot3, ezcontour, conctourf, ezpolar, ezmesh, ezmeshc, ezsurf, ezsurfc1. ezplot：画符号函数图形ezplot（f）：对于显式函数f=f（x），在默认的范围[-pi<x<pi]上画函数f（x）；对于隐函数f=f（x，y），在默认的平面区域[-pi<x<pi，-pi<y<pi]上画函数f（x，y）的图像。

ezplot（f，[min,max]）：在指定的范围[min<x<max]内画函数表达式f=f（x）。

若没有图形窗口存在，则该函数先生成标题为Figure No.1的新窗口，再在该窗口中操作；若已经有图形窗口存在，这在标号最该的图形窗口中进行操作。

ezplot(f,[xmin xmax],fing):在指定标号为fign的窗口中、指定范围[xmin xmax]内画函数f=f(x)的图形。

ezplot(f,[xmin,xmax,ymin,ymax]):在平面矩形区域[xmin<x<xmax,ymin<y<ymax]上画出f(x,y)=0的图像。

ezplot(x,y)：在默认范围0<t<2pi内画出参数形式函数x=x(t)与y=y(t)的图形。

ezplot(x,y,[tmin,tmax)]：在指定范围[tmin<t<tmax]内画参数形式函数x=x(t)与y=y(t)的图形。

ezplot(…，figure)：在由参量文件figure句柄指定的图形窗口中画函数图形。

例如：画下面的隐函数>> syms x y>> ezplot(2*x^4-y^9)2. ezplot3：三维曲线图ezplot3(x,y,z):在默认的范围0<t<2pi内画参数形式的曲线x=x(t),y=y(t),z=z(t)图像。

de算法计算二元函数matlab代码二元函数是指具有两个自变量和一个因变量的函数。

在数学中，我们可以使用不同的算法来计算二元函数的值。

其中一个常用的算法是使用离散值的方法来计算二元函数。

以下是一个使用MATLAB编写的示例代码，用于计算二元函数： ```matlab% 创建一个二元函数的离散值矩阵[x, y] = meshgrid(-5:0.1:5); % 定义自变量的范围及步长z = sin(x) + cos(y); % 定义二元函数% 绘制二元函数图像figure;surf(x, y, z);xlabel('x');ylabel('y');zlabel('z');title('二元函数图像');% 计算给定点的函数值point_x = 1; % 给定点的x坐标point_y = 2; % 给定点的y坐标point_z = sin(point_x) + cos(point_y); % 计算给定点的函数值disp(['给定点的函数值为：', num2str(point_z)]);```在上述代码中，我们首先通过使用`meshgrid`函数创建了一个离散值的网格，其中包括了自变量`x`和`y`的范围和步长。

然后，我们定义了一个二元函数`z`，通过使用自变量`x`和`y`进行计算。

接下来，我们使用`surf`函数绘制了二元函数的图像。

最后，我们给定了一个点的坐标，并计算了该点处的函数值。

您可以根据需要修改上述代码中的函数和自变量的定义，以计算不同的二元函数。

此外，您还可以使用其他算法来计算二元函数的值，例如使用插值方法或数值方法等。

03 函数作图1 平面图形（1）竖直条形图调用格式为：bar(x,y)（2）用描点法绘制函数y f ( x) 随x 从a 到b 间的图形．调用格式为：x=a：h：b ;y=f(x) ;plot(x,y)（3）在同一坐标系下绘制多个函数图形．调用格式为：x=a：h：b ;plot(x,y1,x,y2,…)（4）绘制函数y=f(x)随x 从a 到b 间的图形．调用格式为：explo t(‘f(x)’, [a,b])（5）x 从xa 到xb和y 从ya到yb间隐函数 f ( x, y) 0 的图形．调用格式为：ezplo t(‘x’,’y’,[xa, x b , y a , y b ])（6）绘制t 从ta 到tb间参数方程x x(t )，y y(t )的函数图形．调用格式为：ezplo t(‘x’,’y’,[ta, t b ])（7）在一坐标系下可以绘制一个或多个显函数图形，对变化剧烈的函数，用此命令来进行较精确的绘画．调用格式为：fplot（’fun(x)’,[a,b]）fplo t (‘[f1(x),f2(x),…]’,[a,b])其中fun(x)可以是自定义函数，[f1(x),f2(x),…]是函数组．（8）绘制散点图．调用格式为：ｓｃａｔｔｅｒ（ｘ，ｙ）2 空间图形（1）空间曲线．调用格式为：plot3(x,y,z)（2）产生一个以向量x 为行，向量y 为列的矩阵．调用格式为：ｍｅｓｈｇｒｉｄ(x,y)（3）空间曲面．调用格式为：ｓｕｒｆ(x,y,z)（4）网格曲面．调用格式为：ｍｅｓｈ(x,y,z)例 1 一次考试成绩0~10 分有0 人，10~20 分有0 人，20~30 分1 人，30~40 分有1 人，50~60 分有2 人，60~70 分有18 人，70~80 分有20 人，80~90 分有9 人，90~100 分有6 人．绘出成绩分析竖直条形图．【matlab 命令】>> x=0:10:90;>> y=[0,0,1,1,0,2,18,20,9,6];>> bar(x,y)【输出结果】20002图１例１输出图像例 2 绘制显函数图形．x（１）设 y 1x 3 2x ， y2000 cos2sin x请分别作出这两个函数在区间 x[20,40] 的图像，然后将它们的图像在一个平面直角坐标系中，并判断方程 y 1x 3 2 x 1500cos x2sin x 有几个实数解．（2）在 x[0,4] 上画出分段函数方法一：【matlab 命令】>> x=-20:0.1:40;>> y1=x.^3-35*x.^2+100*x+1500; >> y2=2000*(cos(x/2)-sin(x)); >> figure(1)>> plot(x,y1,'b-'); >> figure(2) >> plot(x,y2,'k');f ( x )32 x 2x 20 x 2 x 2的图像>> figure(3)>> plot(x,y1,'b-',x,y2,'k')【输出结果】图２例2（1）函数y1图３ 例 2（1）函数 y 2 输出图像图４例 2（1）函数 y 1 和 y 2 输出图像 从图中知：有 7 个交点，也就是有 7 个实数根．说明：绘制图形着色时，g 表示绿色，r 表示红色，b 表示蓝色，k 表示黑色．方法二：【matlab 命令２】％自定义函数Ｍ文件ｆｘ１ function y1=fx1(x)y1=x^3-35*x.^2+100*x+1500％自定义函数Ｍ文件ｆｘ２ function y2=fx2(x)y2=2000*(cos(x/2)-sin(x));Ｍａｔｌａｂ命令窗口输入以下命令： >> figure(1)>> fplot('fx1(x)',[-20,40]); >> figure(2)>> fplot('fx2(x)',[-20,40]); >> figure(３)>> fplot('[fx1(x) , fx2(x)] ', [-20,40]); 【输出结果２】结果同上．【matlab 命令３】>> x=0:0.01:2;>> y=(2*x-x.^2).^(1/3);>> plot(x,y,'k','linewidth',2)>> hold on>> x=2:0.01:4;>> y=x-2;>> plot(x,y,'k','linewidth',2)【输出结果３】图５例２（２）函数ｆ（ｘ）的输出图像例３绘制隐函数和参数方程所确定函数的图形．（１）在x [3,3] 上画隐函数x 2 2 9 的图像．（２）在t [0,2] 上画参数方程x cos3 t ，y sin 3 t 的图像．【matlab 命令１】>> ezplot('x^2+y^2-9',[-3,3])>> axis equal【输出结果１】图６例３（１）输出图像说明：axis on 显示坐标轴，axis off 取消坐标轴，grid on 表示加网格线，grid off 表示不加网格线，clf 清楚图形窗口中的图形．也可以通过编辑图像的方法改变或增加设置，比如在图形窗口中，菜单栏Ｔｏｏｌｓ中鼠标选中Ｅｄｉｔ－Ｐｌｏｔ，可改变图像的颜色．【matlab 命令２】>> ezplot('cos(t)^3','sin(t)^3',[0,2*pi])【输出结果２】图７例３（２）输出图像例４将图４，５，６，７在同一个图形窗口表现出来．【matlab 命令】clfsubplot(2,2,1)x=-20:0.1:40;y1=x.^3-35*x.^2+100*x+1500;y2=2000*(cos(x/2)-sin(x));plot(x,y1,'b-',x,y2,'k');subplot(2,2,2)x=0:0.01:2;y=(2*x-x.^2).^(1/3);plot(x,y) holdon x=2:0.01:4;y=x-2;plot(x,y)subplot(2,2,3)ezplot('x^2+y^2-9',[-3,3])axis equal subplot(2,2,4)ezplot('cos(t)^3','sin(t)^3',[0,2*pi])【输出结果】图８ 例４输出图像例５已知平面内８个散点的坐标（1,15,2,20（3,27（4,36（5,49，（6,65（7,87（8,117，在直角坐标系中绘制点图．【matlab 命令】 clf x=1:8; y=[15.3,20.5,27.4,36.6,49.1,65.6,87.8,117.6]; scatter(x,y,'ko') 【输出结果】图9例6 在区间[0,10] 上画出参数曲线x sin t, y cos t, z t ．【matlab 命令】clft=0:pi/50:10*pi;plot3(sin(t),cos(t),t)【输出结果】图１０例７画函数Z ( X Y) 2 的图形．【matlab 命令】clfx=-3:0.1:3; y=1:0.1:5;[X,Y]=meshgrid(x,y);Z=(X+Y).^2;surf(X,Y,Z)shading flat【输出结果】图１１例８画出马鞍曲面Z X 2 Y2 在不同视角的网格图．【matlab 命令】clfx=-3:0.1:3; y=1:0.1:5;[X,Y]=meshgrid(x,y);Z=X.^2-Y.^2;mesh(X,Y,Z)【输出结果】图１２3 习题１．某城市一年１２个月的日平均气温（单位： 0C ）分别为：－１０，－６，５，１０，２０，２５，３０，２４，２２，１９，１０，６，试画出条形图． ２．作出函数 f ( x )cos(e x ) e x / 2) 在区间 x [4,4] 的图形３．作隐函数 sin( xy ) 0 在 [6,6] 内的图形．cos x 2 x 2 ４．已知分段函数 y x x 1 ，作出 15 x 15 的函数图形． 2 sin( x 1) 1x 1５．在同一直角坐标系中，作出函数 y5 的图形和函数 x 3 的图形．６．已知sin( x 2 2 )７．绘制空间图形：（墨西哥帽子）．x 2 2。