《信息论》(电子科大)第3章 离散信源无失真编码

设信源输出符号集合，每次信源输
9
是⼀一个离散⽆无记忆信源，其概率空间为
其中
信源X的符号集合为
N次扩展信源X N符号集合为
15
的有记忆平稳信源（⼆二维平稳信源）输
23
当且仅当X 1和X 2统计独⽴立时等号成⽴立，此时信源相当于⼆二次⽆无记忆扩展；
当X 1和X 2之间相关时，联合熵⼩小于信息熵之和，即⼩小于单个消息符号X 熵的 2 倍。

由于
25
例：设某⼆二维离散信源X =的原始信源X 的信源模型为
中前后两个符号的条件概率
7/92/901/83/41/80
2/11
9/11
(1)若该信源为⼆二维⽆无记忆扩展信源，求信源的熵。

(2)若该信源为⼆二维平稳信源，如表，求信源的熵。

26
原始信源的熵为：
由条件概率确定的条件熵为：
由于符号之间的依赖性，条件熵⽐比信源熵减少了0.672bit
⼆二维离散⽆无记忆扩展信源的熵为：2H(X)=2*1.542=3.084(bit ）7/92/901/83/4
1/8
2/119/11
27
信源X=
平均每发⼀一个消息所能提供的信息量，即联合熵
则每⼀一个信源符号所提供的平均信息量
⼩小于信源X所提供的平均信息量H(X)=1.542bit，这是
由于符号之间的统计相关性所引起的。

28
维平稳信源输出序列每N个符号⼀一组；各
30
则有：
时：
随N的增加是⾮非递增的；
给定时，平均符号熵≥条件熵；
–平均符号熵随N增加是⾮非递增的；
34
解：
35
1,2,......,J 某时刻随机
……
43
44。

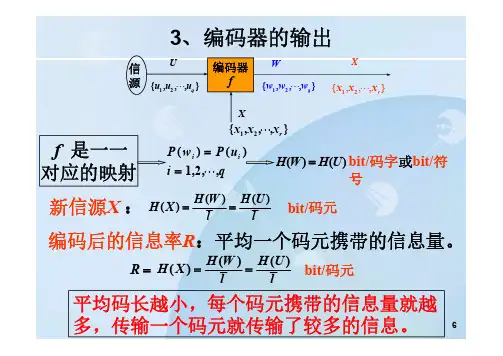
3、编码器的输出f 是一一对应的映射i i P w P u i q()()1,2,, H W H U ()()bit/码字或bit/符号H W H U H X l l()()()bit/码元新信源X ：编码后的信息率R ：平均一个码元携带的信息量。

H W H U H X l l()()()bit/码元平均码长越小，每个码元携带的信息量就越多，传输一个码元就传输了较多的信息。

R X{,,,}12r x x x 编码器f12{,,,}q u u u 12{,,,}r x x x WU12{,,,}q w w w X信源4、编码效率为了衡量编码效果，定义编码效率：编码后的实际信息率与编码后的最大信息率之比。

max max ()()()()log log c R H X H U l H U R H X r l r注：编码效率实际上也是新信源X 的信息含量效率或熵的相对率。

新信源的冗余度也是码的冗余度：1c c X{,,,}12rx x x 编码器f12{,,,}q u u u 12{,,,}r x x x WU12{,,,}q w w w X信源5种不同的码i P u W W W W W U u u u u 351241234()1200001001401000010011810100111001118111110111111W 1: 定长码。

W 3: 变长码。

奇异码。

定长非奇异码肯定是UDC u u u u u u u u u u u u u12434321121211,00,10,010110,01,00,11,00,1,00,1W 2: 定长码。

W 4: 变长码。

W 5: 变长码。

非奇异码。

非奇异码。

非奇异码。

非奇异码。

续长码。

非续长码。

续长码。

及时码。

非及时码。

奇异码肯定不是UDC不是UDC非续长码肯定是UDC 是UDC非及时码。

非续长码。

W 3：1001001唯一可译码定长非奇异码非续长码非奇异码码奇异码非奇异码非唯一可译码唯一可译码定长非奇异码变长非续长码（部分）变长续长码4.3 定长编码定理和定长编码方法1、对信源输出的符号序列进行编码DMS编码器f12{,,,}q u u u 12{,,,}r x x x WU 12{,,,}q w w w XX12{,,,}r x x x DMS编码器f 12{,,,}N q 12{,,,}r x x x WNU 12{,,,}Nq w w w XX12{,,,}r x x x 对信源U 的单个符号进行编码对信源U 的N 长符号串进行编码对扩展信源U N 的单个符号进行编码12i i i iNu u u 1212,,,{,,,}i i iN q u u u u u u2、定长编码定理r 进制定长编码,码长为l N , 可用的码字数目：Nl r Nl Nrq唯一可译max max ()log ()log log N r H U l q H U N r r信息传输率编码效率()()/N H U R H X l Nmax ()()()log c NH X H U l H X r Nbit/码元DMS编码器f 12{,,,}Nq 12{,,,}r x x x W NU 12{,,,}N q w w w XX12{,,,}r x x x定长无失真编码定理：用r 元符号表对离散无记忆信源U 的N 长符号序列进行定长编码，N 长符号序列对应的码长为l N ，若对于任意小的正数ε，有不等式:就几乎能做到无失真编码，且随着序列长度N 的增大，译码差错率趋于0。

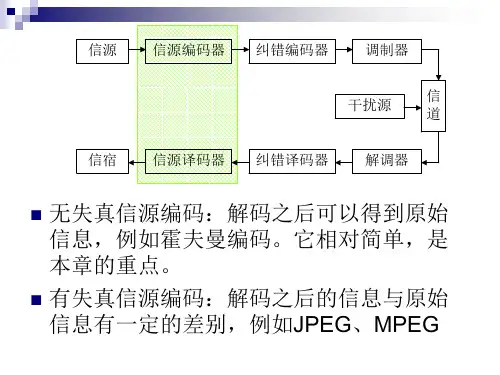
信息理论与编码主要内容⏹第1章绪论⏹第2章信息的度量⏹第3章信道模型和信道容量⏹第4章离散无记忆信源无失真编码⏹第5章有噪信道编码⏹第6章限失真信源编码⏹第7章网络信息论基础⏹第8章信息安全与密码学基础第4章离散无记忆信源无失真编码信息传输系统编码和译码示意图噪声信道U X信源编码信源信宿等效无噪信道信源译码信道编码信道译码Y ˆW WˆU信源编（译）码和信道编（译）码无失真编码和有失真编码无失真信源编码的作用本章主要内容⏹4.1 信源编码概论⏹4.2 码的唯一可译性⏹4.3 定长编码定理和定长编码方法⏹4.4 变长编码定理⏹4.5 变长编码方法⏹4.6 几种实用的无失真信源编码4.1 信源编码概论信源编码器示意图定长编码和变长编码平均码长编码效率信源编码器示意图——信源符号集合；——码元组成的集合；——信道能够传送的符号，称为码元；——信源编码，一一对应映射，——把信源输出的符号变换成的码元序列，称为码字；——所有码字组成的集合，称为码或码字集。

——所含码元的个数，称为该码字的码长，单位“码元/符号”或编码器12{,,,}q u u u L 12{,,,}r x x x L WU12{,,,}q w w w L X信源12{,,,}q U u u u =L 12{,,,}rX x x x =L i x fi i w u −→−1,2,,i q=L i w i u 12{,,,}q W w w w =L U i l iw定长编码和变长编码平均码长小说明平均一个码元所携带的信息量大，信l 12r l l l l ====L l11()()qqiiiii i l P w lP u l====∑∑11()()q qi i i i l P u l l P u l=====∑∑ll例123412141818UU u u u uP⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦{0,1}X=1111122213331444()00,2()01,2()10,2()11,2f u w lf u w lf u w lf u w l============ 411111()222222488i iil P u l===⨯+⨯+⨯+⨯=∑2111222223332444()0,1()10,2()110,3()111,4f u w lf u w lf u w lf u w l============ 411111()1233 1.752488i iil P u l===⨯+⨯+⨯+⨯=∑编码效率X编码器12{,,,}qu u uL12{,,,}rx x xLWU12{,,,}qw w wLX信源X12{,,,}rx x xLiuiw()()i iP w P u=1,2,,i q=L()()H W H U=cη()()()H W H UH Xl l==()()H UR H Xl==max max()()()()log log cR H X H U l H UR H X r l r η====1c cγη=-4.2 码的唯一可译性⏹4.2.1 常见码及其唯一可译性⏹4.2.2 码树和Kraft 不等式4.2.1 常见码及其唯一可译性唯一可译码和非唯一可译码码W 是唯一可译码的充分必要条件奇异码和非奇异码非续长码和续长码及时码或立即码各种码的关系唯一可译码和非唯一可译码码是唯一可译码的充分必要条件35124121142183184()0000100010*******101001110011111110111111 iP u W WW W WUuuuu奇异码和非奇异码非续长码和续长码及时码或立即码各种码的关系唯一可译码定长非奇异码非续长码非奇异码4.2.2 码树和Kraft 不等式码树节点l 阶节点终端节点端点114w3w2w1w1()a1114w3w2w1()b一阶节点1114111w=1w=113011w=201w=()c二阶节点三阶节点il1,2,,i q=L11iqlir-=≤∑il1,2,,i q=L11iqlir-=≤∑4.3 定长编码定理和定长编码方法定长编码惟一可译条件定长无失真编码定理定长编码惟一可译条件[,][,()|1,2,,]U i iU P u P u i q==L UN NU N qNlNl Nl N l rNUNl Nr q≥Nqmaxmax()log()log logNrl H UqH UN r r≥==Nl Nmax()rH U UUUUNl Nmax()rH UN定长无失真编码定理UNN NNNl ε()logNl H UN rε+≥()2logNl H UN rε-≤()()log logcNH U H Ull r rNη==Ul ()rH U例1解{0,1}X=UU123456723456611111112222222 Uu u u u u u u UP⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦log log72.8log log2Nl qlN r=≥=≈X U1234567 ::001010011100101110111 U u u u u u u u W7163 ()()log()32i iiH U P u P u==-=∑3l l==6332()65.625%log3log2cH Ul rη===⨯U()()()log ()log c N H U H U H U l l r H U r Nηε===+e P 22()e U P N σε≤2()U σU[]{}[][]22221()()()()log ()()q i i i i U E I u H U P u P u H U σ==-=-∑δ22()U N σεδ>eP δ<[]2222()(1)()cc U N H U ησηδ>-例2解()6332H U=[][]2221()()log()() 5.0625 qi iiU P u P u H Uσ==-=∑[][]2228 222226() 5.0625(0.9)10(1)(10.9)10()6332ccUNH Uησηδ->=≈--⨯810N>90%cη=610δ-<4.4 变长编码定理无失真变长编码定理（香农第一定理）()NrlH UNNl1()NrlH UN N<+lim lim()NrN Nll H UN→∞→∞==()()lim lim lim100%logrcN N NH UH Ul r lη→∞→∞→∞===4.5 变长编码方法最佳码最佳编码最佳码本节主要内容⏹4.5.1 霍夫曼编码⏹4.5.2 费诺编码⏹4.5.3 香农编码4.5.1 霍夫曼编码二进制霍夫曼编码编码效果分析r进制霍夫曼编码符号序列的霍夫曼编码二进制霍夫曼编码iu 符号概率)(i u P 码字i w 码长il 1u 212u 2213u 3214u 4215u 5216u 6217u 621110120013000140000150000016000000652111 11111.0042132122121234566 11111111234566 2222222l=⨯+⨯+⨯+⨯+⨯+⨯+⨯6332=63326332()100%log log2cH UN rη===⨯编码效果分析max()6332110.3()log7H UH Uγ=-=-≈110.656250.34375cγ=-=210.90.1cγ=-=3110 cγ=-=1234567 ::001010011100101110111 U u u u u u u u W⎥⎦⎤⎢⎣⎡===⎥⎦⎤⎢⎣⎡)1()0(1XPXPPXX分别为和(0)l(1)l2345661111111115(0)2212110222222264l=⨯+⨯+⨯+⨯+⨯+⨯+⨯=11577(1)(0)36464l l l=-=-=(0)11564(1)7764(0)0.6(1)0.433l lP X P Xl l===≈===≈12612234566111111163 (0)0123456222222264 l=⨯+⨯+⨯+⨯+⨯+⨯+⨯=636363(1)(0)326464l l l=-=-=(0)6364(0)0.5(1)1(0)0.56332lP X P X P Xl======-==例1解12345670.350.300.200.100.040.0050.005UU u u u u u u uP⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦iu 符号概率)(i u P 码字i w 码长il 1u 2u 3u 4u 5u 6u 7u 0.35110.300120.2000130.10000140.040000150.00500000160.005000000611 111101.000.010.050.150.350.65iu 符号概率)(i u P 码字i w 码长il 1u 2u 3u 4u 5u 6u 7u 0.351120.301020.200120.1000130.04000140.0050000150.00500000511111100 0 1.000.010.050.150.350.65。