当前位置：文档之家 › 第三章-统计模式识别中的概率分类法PPT课件

第三章-统计模式识别中的概率分类法PPT课件

  • 格式：ppt
  • 大小：2.79 MB
  • 文档页数：127

下载文档原格式

  / 127

合集下载

模式识别(3-1)

模式识别(3-1)

§3.2 最大似然估计
最大似然估计量： －使似然函数达到最大值的参数向量。 －最符合已有的观测样本集的那一个参数向量。 ∵学习样本从总体样本集中独立抽取的
N ) p( X | ) p( X k | i ) k 1 N个学习样本出现概率的乘积
i
i
∴
p( X | i . i
i
§3.2 Bayes学习
假定： ①待估参数θ是随机的未知量 ②按类别把样本分成M类X1，X2，X3，… XM 其中第i类的样本共N个 Xi = {X1,X2,… XN} 并且是从总体中独立抽取的 ③ 类条件概率密度具有某种确定的函数形式，但其 参数向量未知。 ④ Xi 中的样本不包含待估计参数θj(i≠j)的信息，不 同类别的参数在函数上是独立的，所以可以对每一 类样本独立进行处理。


有时上式是多解的, 上图有5个解,只有一个解最大即 （对所有的可能解进行检查或计算二阶导数）
§3.2 最大似然估计
例：假设随机变量x服从均匀分布，但参数1， 2未知， 1 1 x 2 p ( x | ) 2 1 ， 0 其他 求1， 2的最大似然估计量。 解：设从总体中独立抽取N个样本x1 , x2 , , xN , 则其似然函数为： 1 p ( x1 , x2 , , xN | 1， 2 ) ( 2 1 ) N l ( ) p ( X | ) 0




§3.2 Bayes学习
p ~ N 0 , 0

2

其中 0和 0 是已知的
2
已知的信息还包括一组抽取出来的样本X i x1 , x2 ,, xN ，从而 可以得到关于 的后验概率密度：

模式识别详细PPT

模式识别详细PPT
迁移学习在模式识别中广泛应用于目标检测、图像分类等任务，通过将预训练模 型（如ResNet、VGG等）应用于新数据集，可以快速获得较好的分类效果。
无监督学习在模式识别中的应用
无监督学习是一种从无标签数据中提取有用信息的机器学习方法，在模式识别中主要用于聚类和降维 等任务。
无监督学习在模式识别中可以帮助发现数据中的内在结构和规律，例如在图像识别中可以通过聚类算 法将相似的图像分组，或者通过降维算法将高维图像数据降维到低维空间，便于后续的分类和识别。
通过专家知识和经验，手 动选择与目标任务相关的 特征。
自动特征选择
利用算法自动筛选出对目 标任务最相关的特征，提 高模型的泛化能力。
交互式特征选择
结合手动和自动特征选择 的优势，先通过自动方法 筛选出一组候选特征，再 由专家进行筛选和优化。
特征提取算法
主成分分析（PCA）
通过线性变换将原始特征转换为新的特征， 保留主要方差，降低数据维度。
将分类或离散型特征进行编码 ，如独热编码、标签编码等。
特征选择与降维
通过特征选择算法或矩阵分解 等技术，降低特征维度，提高 模型效率和泛化能力。
特征生成与转换
通过生成新的特征或对现有特 征进行组合、转换，丰富特征
表达，提高模型性能。
04
分类器设计
分类器选择
线性分类器
基于线性判别分析，适用于特征线性可 分的情况，如感知器、逻辑回归等。
结构模式识别
总结词
基于结构分析和语法理论的模式识别方法，通过分析输入数据的结构和语法进行分类和 识别。
详细描述
结构模式识别主要关注输入数据的结构和语法，通过分析数据中的结构和语法规则，将 输入数据归类到相应的类别中。这种方法在自然语言处理、化学分子结构解析等领域有

[课件]第三章 概率和统计推断PPT

[课件]第三章 概率和统计推断PPT

●●数理统计已证明： 当 x = μ ± 1 .9 6 δ 时 ， 正 态 曲 线 下 的 面 积 即 累 积 概 率 P = 9 5 % ； 当 x = μ ± 2 .5 8 δ 时 ， 正 态 曲 线 下 的 面 积 即 累 积 概 率 P = 9 9 % 。
f(x)
0 μ
x
图 3 -1
正态分布的图形

x
Hale Waihona Puke E (x) x E ( ) n 1 E ( x) n 1 E (x) n 1 n 1 n n
● ● 样 本 平 均 数 分 布 的 方 差 等 于 总 体 方 差 除 以 样 本 容 量 ：即

2 x
2 n
D (x) D ( 1 n 1 n 1
总体
„ 样本 1 样本 2 样本 3 无穷个样本
图 3-5 总体和样本的关系示意
1． 抽 样 分 布 的 基 本 知 识 ●从总体中抽样必须符合随机的原则。 ●从总体中随机抽样的方法有 2 种 复置抽样——指每次抽出一个个体进行观测后，应放回到原总体中。 不 复 置 抽 样 — —指 每 次 抽 出 的 个 体 观 测 后 ， 不 再 放 回 原 总 体 。 复置与否，对无限总体而言关系不大，都可保证各个个体被抽到的机 会均等。但对于有限总体，要保证随机抽样，必须采用复置抽样。 ●母总体和衍生总体
e P(x r) r!
●普瓦松分布的参数 总体平均数： 2 np 总体方差： 总体标准差：


r
●普瓦松分布的图形 普瓦松分布的图形随μ 而变。 当 μ ＜ 1 时 ， 图 形 呈 反 “ J” 字 形 ；
np
np

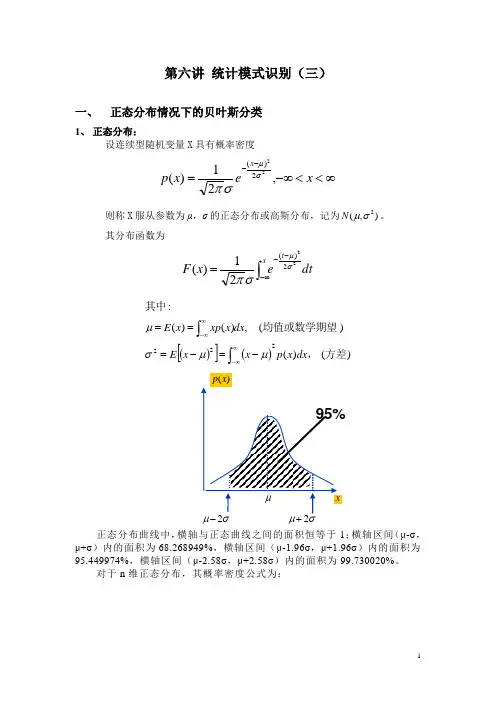
第六讲 统计模式识别(三)

第六讲 统计模式识别(三)

第六讲 统计模式识别（三）一、 正态分布情况下的贝叶斯分类1、 正态分布：设连续型随机变量X 具有概率密度∞<<-∞=--x ex p x ,21)(222)(σμσπ则称X 服从参数为μ，σ的正态分布或高斯分布，记为),(2σμN 。

其分布函数为dt ex F xt ⎰∞---=22)(21)(σμσπ()[]())()()(,)()(:222方差，均值或数学期望其中dx x p x x E dx x xp x E ⎰⎰∞∞-∞∞--=-===μμσμ正态分布曲线中，横轴与正态曲线之间的面积恒等于1；横轴区间（μ-σ，μ+σ）内的面积为68.268949%，横轴区间（μ-1.96σ，μ+1.96σ）内的面积为95.449974%，横轴区间（μ-2.58σ，μ+2.58σ）内的面积为99.730020%。

对于n 维正态分布，其概率密度公式为：()()()()∑∑∑∑∑--∑⨯==⎥⎦⎤⎢⎣⎡---∑=的行列式为的逆阵，为维协方差矩阵，为维均值向量，维特征向量其中121211212),...,,(,,...,,:21exp ||21)(d d d d x x x x p Td Td Tdμμμπμx μx μx均值向量μ的分量μi 为：i i i i i dx x p x x E ⎰∞∞-==)()(μ协方差矩阵为：()()[]()()()()[]()()()()()()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--------=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=--=∑d d d d d dd d d d d d Tx x x x x x x x E x x x x E E μμμμμμμμμμμμ,...,......,...,,...,......111111111111μx μx()()[]()()[]()()[]()()[]⎪⎪⎭⎫ ⎝⎛≠=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--------=是协方差，非对角线是方差对角线j i j i x x E x x E x x E x x E ij ij dd d d d d d d d d d d d 22222212121221111111111,,..............................σσσσσσσσμμμμμμμμ 多维正态分布具有以下性质：μ与∑对分布起决定作用, μ由d 分量组成，∑由d(d+1)/2个元素组成，所以多维正态分布由d+d(d+1)/2个参数组成。

统计与概率ppt课件

统计与概率ppt课件

占总数的百分比。
从图中能清晰地看出 作用 各数量的多少，便于
相互比较。
从图中既能看出数量的多 从图中能清晰地看出各部
少，也能清晰地看出数量 分占总体的百分比，以及
的增减变化情况。
部分与部分之间的关系。
-
3.条形统计图绘制的步骤和方法：（1）根据纸张的大小画出两条互相垂 直的射线；（2）通常在横轴上适当分配条形的位置，确定直条的宽度和间隔 ；（3）通常在纵轴上根据数据大小的具体情况，确定单位长度；（4）按照 数据的大小画出长短不同的直条，并标明数量；（5）写上统计图的名称并标 明制图时间。
-
统计
续表
（3）扇形统计图用整个圆表示总数，用圆内的扇形表示各部分，扇形统计 图可以清楚地反映出各部分与总数之间的关系。 3.平均数：总数量÷总份数=平均数。
1.生活中，有些事件的发生是不确定的，一般用“可能”来描述，有些事件 的发生是确定的，一般用“一定”或“不可能”来描述。 2.事件发生的可能性是有大小的，事件发生的可能性的大小与物品数量的多 可能性 少有关。数量多，可能性大；数量少，可能性小。 3.体验事件发生的等可能性及游戏规则的公平性，能设计出公平的、符合指 定要求的游戏规则。
-
例 1 丽丽统计的本班20位学生体重如下。（单位：kg） 男生：37 42 39 40 46 41 40 43 44 39 女生：29 32 40 41 27 35 36 33 34 38 数一数，把下面的统计表补充完整。
体重/kg 32以下
32～35
36～39
40～43错答案：0 0 3 5 2 错因分析：错解只统计了10位男生的体重情况，而统计表是汇总的20位 同学的整体体重情况。 满分备考：根据各初始数据统计整理数据时，一定要做到不重不漏。

模式识别的分类算法ppt课件

模式识别的分类算法ppt课件
2. 在新样本到达后，提取特征,确定新样本的 特征向量表示
3. 在训练集中选出与新样本最相似的 K 个文 样本，计算公式为：
可编辑课件
7
4.在新样本的K个邻居中，依次计算每类的 权重计算公式如下：
5. 比较类的权重，将文本分到权重最大的那个 类别中。
可编辑课件
8
KNN
可编辑课件
9
LDA
• 线性判别式分析 (Linear Discriminant Analysis, LDA)，
模式识别又常称作模式分类
可编辑课件
3
分类
• 有监督的分类（Supervised Classification） • 无监督的分类(Unsupervised Classification)
二者的主要差别在于： 各实验样本所属的类别是否预先已知。
可编辑课件
4
应用领域
• 主要应用领域是图像分析与处理、语音 识别、声音分类、通信、计算机辅助诊 断、数据挖掘等学科。
• CW-SSIM BASED IMAGE CLASSIFICATION IEEE International Conference on Image Processing
可编辑课件
20
Thank you!
可编辑课件
21
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
• 基本思想：将高维的模式样本投影到最 佳鉴别矢量空间，以达到抽取分类信息 和压缩特征空间维数的效果，投影后保 证模式样本在新的子空间有最大的类间 距离和最小的类内距离
即模式在该空间中有最佳的可分离性
可编辑课件
10
LDA
假设对于一个n维空间有m个样本分别为

模式识别(统计决策方法)PPT课件

p＝P(A)
实际上，求出的P为频率，但是如果统计次数足够大，可以 认为此时的频率接近概率 可见概率就是频率的稳定中心。任何事件A的概率为
0＜=P(A)＜=1
条件概率:我们把事件B已经出现的条件下，事件A发生的概 率记做为P(A|B)。并称之为在B出现的条件下A出现的条件概 率，而称P(A)为无条件概率。
称满足上述条件的, A1,A2,…,An为完备事件组.
另有一事件B = BA1+BA2+…+BAn
条件概率公式
P(AiB)＝P(Ai)·P(B|Ai)
A1
A3
An
B
n
P(B) P( Ai )P(B | Ai )
A2
i 1
自动化学院
.
13
贝叶斯公式推导 全概率公式
Ai∩Aj=Φ
BAi BAj , P(BAi ) P(BAj ) P(BAi BAj )
= P(点目标)P(目标丢失|点目标)+P(斑目标)P(目标丢失|斑目 标) =0.4×0.01+0.6×0.02=0.016
自动P(化成学功院检测目标)=1-P（目标丢失）=98.4%
.
15
贝叶斯公式推导
全概率公式
诸Ai是原因，B是结果
由此可以形象地把全概 率公式看成为：
“由原因推结果”，每 个原因对结果的发生有 一定的“作用”，即结 果发生的可能性与各种 原因的“作用”大小有 关. 全概率公式表达了它 们之间的关系 .
n
,
P(Aj )P(B | Aj )
j 1
i 1, 2, , n
该公式于1763年由贝叶斯(Bayes)给出，它是在观察到事件 B已发生的条件下，寻找导致B发生的每个原因的概率.

模式识别基础教程PPT课件


8
典型应用
语音识别（例如：IBM ViaVoice系统） 表情分析、年龄、种族、性别分类 OCR: 车牌照、集装箱号码… 手写体识别：汉王 手势识别：基于视觉的，基于数据手套 人脸识别、指纹识别、虹膜识别… 军事目标识别 生物信息、医学图像 遥感、气象
9
模式识别方法
模板匹配 结构模式识别 句法模式识别 统计模式识别 模糊模式识别
机特征向量，用概率统计理论对其进行建模， 用统计决策理论划分特征空间来进行分类。
12
统计模式识别的一般过程
测试模式 预处理
分类
训练 预处理
训练模式
特征提 取/选择
分类
特征提 取/选择
学习分类规则 错误率检测
13
模糊模式识别
1965年Zadeh提出模糊集理论
是对传统集合理论的一种推广
传统：属于或者不属于 模糊：以一定的程度属于
这种技术具有实时性的特点，而且有可能扩展到多个姿 态的人脸检测。
18
人脸的特征表示方法
矩形特征（Harr-like特征）
矩形特征的值是所有白色矩形中点的亮度值的和减 去所有灰色矩形中点的亮度值的和，所得到的差
有4种类型的矩形特征
19
输入图像
积分图像
基于积分图像的 Haar-like特征计
7
模式分类 vs. 模式聚类
Classification Clustering
Category “A”
Categ
(Supervised Classification)
Clustering
(Unsupervised Classification)
“Good” features
“Bad” features

模式识别-3-贝叶斯决策理论


(
)
确定性特征向量与随机特征向量
确定性特征向量 在获取模式的观测值时，有些事物具有确定的 因果关系，即在一定条件下，存在必然会发生 或必然不发生的确定性，这样获得的特征向量 称为确定性特征向量。 例如识别一块模板是不是直角三角形，只要 凭“三条直线边闭合连线和一个直角”这个 特征，测量它是否有三条直线边的闭合连线 并有一个直角，就完全可以确定它是不是直 角三角形。 这种现象是确定性的现象，比如上一讲的线 性模式判别就是基于这种现象进行的。
x1 x X = 2 ... xn
特征向量
g1(x) g2(x)
...
Max(g(x))
最大值选择器
x ∈ ωi
gn(x)
判别计算
决策
§3-3 正态分布决策理论
一、正态分布判别函数
1、为什么采用正态分布：
a、正态分布在物理上是合理的、广泛的。 b、正态分布数学上简单，N(µ, σ ²) 只有均值和方差两个参数。
)
2
=
∫ (x − µ )
−∞
∞
2
P ( x)
P ( x ) d x，方 差 ) (
1
概率密度函数应满足下 列关系： P ( x ) ≥ 0, ( −∞ < x < ∞ ) ∞ ∫−∞ P ( x )dx = 1
0 . 95
µ − 2σ
µ
X
µ + 2σ
3、（多变量）多维正态分布 （1）函数形式：
µ i = E ( xi ) =
∑
= E
= E = E
(x 1 − ...... (x n − µ
[(x

模式识别(PPT)


第一章 模式识别概论
什么是模式（Pattern）？
什么是模式？
• 广义地说，存在于时间和空间中可观察的物 体，如果我们可以区别它们是否相同或是否 相似，都可以称之为模式。 • 模式所指的不是事物本身，而是从事物获得 的信息，因此，模式往往表现为具有时间和 空间分布的信息。 • 模式的直观特性:
结构模式识别
• 该方法通过考虑识别对象的各部分之间的联 系来达到识别分类的目的。 • 识别采用结构匹配的形式，通过计算一个匹 配程度值（matching score）来评估一个未知 的对象或未知对象某些部分与某种典型模式 的关系如何。 • 当成功地制定出了一组可以描述对象部分之 间关系的规则后，可以应用一种特殊的结构 模式识别方法 – 句法模式识别，来检查一个 模式基元的序列是否遵守某种规则，即句法 规则或语法。
实例：句法模式识别（续）
• 多级树描述结构
实例：句法模式识别（续）
• 训练过程：
– 用已知结构信息的图像作为训练样本，先 识别出基元（比如场景图中的X、Y、Z等 简单平面）和它们之间的连接关系（例如 长方体E是由X、Y和Z三个面拼接而成）， 并用字母符号代表之； – 然后用构造句子的文法来描述生成这幅场 景的过程，由此推断出生成该场景的一种 文法。
模式识别
- 概念、原理及其应用
引 言
课程对象
• 计算机应用技术专业硕士研究生的专业 基础课 • 电子科学与技术学科硕士研究生的专业 基础课
与模式识别相关的学科
• • • •
• • • • •
统计学 概率论 线性代数（矩阵计算） 形式语言
机器学习 人工智能 图像处理 计算机视觉 …
教学方法
• 着重讲述模式识别的基本概念，基本方 法和算法原理。 • 注重理论与实践紧密结合
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

有一个 a c 维风险矩阵。
类型 判决
1
2
一般风险矩阵
w1 L(1 | w1) L( 2 | w1)
w2 L(1 | w2 ) L(2 | w2 )
…… …… …… ……
wc L(1 | wc ) L( 2 | wc )
若令 t 为两类分界面，特征向量 x 为一维时，t 为 x 轴上的一个
点，如上图所示：
t

P(e) P(w2 | x) (x)dx t P(w1 | x)(x)dx
t
Hale Waihona Puke (x | w2 ) P(w2 )dx t (x | w1 ) P(w1 )dx
例如：一个 2 类问题，w1 表示诊断为无癌症，w2 诊断为有癌症。P(w1) 表示诊断正常的概率，P(w2) 表示某地区的人被诊断出患上癌症的概 率，该值可以通过大量的统计得到，x 表示“试验反应呈阳性”。那
么，P(x|w1)表示诊断为无癌症且试验反应为阳性，P(w1|x)表示试验
为阳性，而且没有癌症。同样，可以有 w2 的类概率密度和后验概率。
先验概率： P(w1) 0.995 ， P(w2 ) 0.005 类条件概率密度： (x | w1) 0.01 ， (x | w2 ) 0.95 （3） 决策过程
(w2 | x)
(x | w2 ) P(w2 )
(x | w1 ) P(w1 ) (x | w2 ) P(w2 )
P(w2 | x) P(w1 | x) ，则 x w2
（3.2－3）
P(w1 | x) P(w2 | x) ，则偶然决定 x w1 ，或 x w2
根据（3.2－2）式，上述判决规则等价于：
(x |w1 ) P(w1) (x |w2 ) P(w2 ) ，则 x w1
如下图所示，在一维特征空间里，判决门限 t 把空间划分为两个 类型区域 R1，R2。
在 R1 中， (x | w1) P(w1) (x | w2 ) P(w2 ) ，则 x w1 ； 在 R2 中， (x | w2 ) P(w2 ) (x | w1) P(w1) ，则 x w2 ；
3.2 最小错误率判决规则（最简单的 Bayes 分类方法）
分析一个“两类问题”。
以上一个例子为例，用 w1 和 w2 表示两种不同的类型，如 w1
表示诊断正常，w2 表示诊断出患有癌症。
用 P(w1) 和 P(w2 ) 分别表示先验概率。如： P(w1) 诊断正常的概率， P(w2 ) 表示某地人患癌症的概率，可通过大量的统计得到。
(x | w1 ) P(w1 ) (x | w2 ) P(w2 )
由最小错误判决规则，可知：甲 w1 由于 P(w1) 比 P(w2 ) 大很多，所以先验概率起了较大作用。
3.3 最小风险判决规则 最小风险判决规则也是一种 Bayes 分类方法。最小错误率判决规 则没有考虑错误判决带来的“风险”，或者说没有考虑某种判决带来 的损失。 同一问题中，某种判决总会有一定的损失，特别是错误判决有风 险。不同的错误判决有不同的风险，如上一节的例子中，判断细胞是 否为癌细胞，可能有两种错误判决： ① 正常细胞错判为癌细胞； ② 癌细胞错判为正常细胞。 两种错误带来的风险不同。在①中，会给健康人带来不必要的精 神负担，在②中，会使患者失去进一步检查、治疗的机会，造成严重 后果。显然，第②种错误判决的风险大于第①种。
这一批人中，每100个正常人中有一个试验呈 阳性反应；
这一批人中，每100个癌症病人中有95人试验 呈阳性反应。
问：若某人（甲）呈阳性反应，甲是否正常？
解：假定 x 表示实验反应为阳性，
（1） 人分为两类：w1－正常人，w2－癌症患者， P(w1) P(w2 ) 1 （2） 由已知条件计算概率值：
第三章-统计模式识别中的概率分类法
3.1 引言 3.2 最小错误率判决规则 3.3 最小风险判决规则 3.4 最大似然比判决规则 3.5 Neyman-Pearsen判决规则 3.6 最小最大判决规则 3.7 分类器设计 3.8 正态分布时的统计决策 3.9 参数估计与非参数估计
许多实际情况，即使在类型A的条件下，模 式样本x位于区域A的概率也往往小于1，而 位于区域B的概率也不为0。对于类型B的条 件也一样。这种交错分布的样本使分类发生 错误，是模式随机性的一种表现。此时，分 类方法就从确定性模式转到随机模式。
“如何使分类错误率尽可能小，是研究各种 分类方法的中心议题。”
所以要使 P(e) 最小，判决门限应如上图所示，否则就会有多余的 阴影面。而（3.2-3）、（3.2-4）表达的判决规则，判决门限正好如上
图所示，所以称之为“最小错误概率判决规则”。
可以把上述两类问题导出的最小错误率判决规则一般化，推广到
c 类问题中，表达为：
若： P(wi
|
x)

max{P(w
j 1,,c
P(w1 ) P(w2 ) P(wc ) 1
其实，在处理实际问题时，有时不得不以先验概率的大小作为判 决的依据。如：有一批木材，其中桦木占 70％，松木占 30％，A―― 桦木，B－－松木，则 P( A) 0.7 ， P(B) 0.3 ，如果从中任取一块木材， 而又要用先验概率作出判决，那就判为桦木。 先验概率不能作为判决的唯一依据，但当先验概率相当大时，它也能 成为主要因素。
阴影区域是两类样本的交错分配区域，阴影面积就是这种分类方
法的错误概率。总错误率有两种情况：
x w1，而判为 x w2 ，斜线区域。 x w2 ，而判为 x w1 ，纹线区域。 所以，总错误率：

P(e) P(e | x)(x)dx
其中，


()dx
表示在整个
d
维特征空间上的积分。
也可写为：
P(e) P(x R1, w2 ) P(x R2 , w1)
P(w2 ) P(x R1 | w2 ) P(w1) P(x R2 | w1)
P(w2 )
R1 (x | w2)dx (w1 )
(x | w1)dx
R2
P(w2 ) P2 (e) P(w1) P1(e)
（3.2－1）
根据 Bayes 公式，在模式样本 x 出现的条件下，两个类型的后验 概率为：
P(w1
|
x)

(x
|w1 ) P(w1 ) (x)
，
P(w2
|
x)

(x
|w2 ) P(w2 ) (x)
（3.2－2）
此时，样本归属于“后验概率较高”的那种类型。
也就是：
P(w1 | x) P(w2 | x) ，则 x w1
Bayes决策理论是随机模式分类方法最重要 的基础。下面是几个重要的概念：
1. 先验概率 先验概率是预先已知的或者可以估计的模式识别系统位于某种类 型的概率。 若仍然用两个类型 A 和 B 为例，可用 P(A) 和 P(B) 表示各自的先验概 率，此时满足 P( A) P(B) 1 。 推广到一般的 c 类问题中，用 w1, w2 ,wc 表示类型，则各自的先验 概率用 P(w1 ), P(w2 ),, P(wc ) 表示，且满足：
先看一下确定性模式判决函数的问题。 如下图所示：
通过判决函数，特征空间
被区分界面划分成两种类型的区 域A和B。由于模式样本的观测 值是确定性的，经常被正确分配 到类型区域A、B之中。假如我 们用概率的形式来表达，就是： 在类型A的条件下观测模式样本 x，则x位于区域A的概率为1， 而位于区域B的概率为0。同样， 在类型B的条件下观测模式样本 x，情况正好相反，x位于区域A 的概率为0，而位于区域B的概 率为1。这实际上是将概率的方 法引入到确定模式，对于大多数 实际情况，这是非常理想的概率 分布。

0.95 0.005
0.01 0.995 0.95 0.005
0.323
(x | w1 ) P(w1 ) 0.00995
P(w1 | x) 1 P(w2 | x) 1 0.323 0.677
(x | w2 ) P(w2 ) 0.00475
P(w1 | x) P(w2 | x)
对上述两类问题：当 P(w2 | x) P(w1 | x) 时，则 x w2 。显然作出决策
w2 时，x 的条件错误概率为 P(w1 | x) ，反之为 P(w2 | x) 。
也就是： P(e | x) =
P(w1 | x) P(w2 | x)
当 P(w2 | x) P(w1 | x) 当 P(w1 | x) P(w2 | x)
2．类（条件）概率密度 它是系统位于某种类型条件下，模式样本 x 出现的概率密度分布 函数，常用 (x | A), (x | B) ，以及 (x | wi )(i 1,2,,c) 来表示。 类概率密度在分类方法中起至关重要的作用，它的函数形式及主 要参数或者是已知的，或者是可通过大量抽样实验估计出来。 3. 后验概率 它是系统在某个具体的模式样本 x 条件下，位于某种类型的概率， 常以 P(A | x), P(B | x) ，以及 P(wi | x)(i 1,2,, c) 表示。 后验概率可以根据贝叶斯公式计算出来，可直接用作分类判决的 依据。
用 (x | w1) 和 (x | w2 ) 表示两个类概率密度。 样本 x 表示“试验反应阳性”，则 (x | w1) 诊断为无癌症且试验反 应为阳性， P(w1 | x) 试验为阳性且没有癌症。 根据全概率公式，模式样本 x 出现的全概率密度为：
(x) (x | w1) P(w1) (x | w2 ) P(w2 )