凸轮例题-文档资料
- 格式:ppt
- 大小:804.50 KB
- 文档页数:9
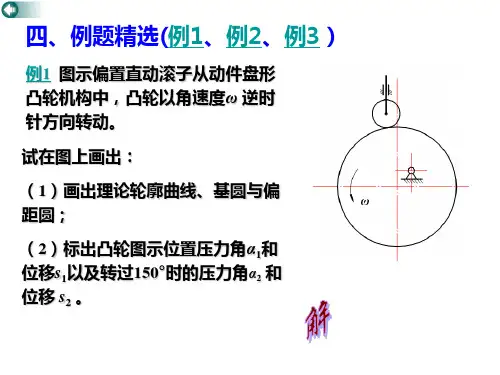

凸轮一、单项选择题(从给出的A、B、C、D中选一个答案)1 与连杆机构相比,凸轮机构最大的缺点是。
A.惯性力难以平衡B.点、线接触,易磨损C.设计较为复杂D.不能实现间歇运动2 与其他机构相比,凸轮机构最大的优点是。
A.可实现各种预期的运动规律B.便于润滑C.制造方便,易获得较高的精度D.从动件的行程可较大3 盘形凸轮机构的压力角恒等于常数。
A.摆动尖顶推杆B.直动滚子推杆C.摆动平底推杆D.摆动滚子推杆4 对于直动推杆盘形凸轮机构来讲,在其他条件相同的情况下,偏置直动推杆与对心直动推杆相比,两者在推程段最大压力角的关系为关系。
A.偏置比对心大B.对心比偏置大C.一样大D.不一定5 下述几种运动规律中,既不会产生柔性冲击也不会产生刚性冲击,可用于高速场合。
A.等速运动规律B.摆线运动规律(正弦加速度运动规律)C.等加速等减速运动规律D.简谐运动规律(余弦加速度运动规律)6 对心直动尖顶推杆盘形凸轮机构的推程压力角超过许用值时,可采用措施来解决。
A.增大基圆半径B.改用滚子推杆C.改变凸轮转向D.改为偏置直动尖顶推杆7.()从动杆的行程不能太大。
A. 盘形凸轮机构B. 移动凸轮机构C. 圆柱凸轮机构8.()对于较复杂的凸轮轮廓曲线,也能准确地获得所需要的运动规律。
A 尖顶式从动杆 B.滚子式从动杆 C. 平底式从动杆9.()可使从动杆得到较大的行程。
A. 盘形凸轮机构 B 移动凸轮机构 C. 圆柱凸轮机构10.()的摩擦阻力较小,传力能力大。
A 尖顶式从动杆 B. 滚子式从动杆 C 平底式从动杆11.()的磨损较小,适用于没有内凹槽凸轮轮廓曲线的高速凸轮机构。
A. 尖顶式从动杆B.滚子式从动杆C. 平底式从动杆12.计算凸轮机构从动杆行程的基础是()。
A 基圆 B. 转角 C 轮廓曲线13.凸轮轮廓曲线上各点的压力角是()。
A. 不变的B. 变化的14.凸轮压力角的大小与基圆半径的关系是()。
A 基圆半径越小,压力角偏小 B. 基圆半径越大,压力角偏小15.压力角增大时,对()。


机械原理凸轮机构习题与答案(五篇材料)第一篇:机械原理凸轮机构习题与答案解:曲柄的存在的必要条件是1)最短杆与追长杆的杆长之和应小于或等于其余两杆的长度之和;2)连架杆与机架必有最短杆1).杆件1为曲柄2).在各杆长度不变的情况下,选取c杆做为机架就可以实现双摇杆机构试以作图法设计一偏置尖底推杆盘形凸轮的轮廓曲线。
已知凸轮以等角速度顺时针回转,正偏距e=10,基园半径r0=30mm.推杆运动规律为:凸轮转角δ=0~150时,推杆00.凸轮转角δ=180~300时推杆等速上升16mm;.凸轮转角δ=150~180时推杆远休;等加速回程16mm;.凸轮转角δ=300~360时推杆近休。
解:解题步骤1)首先绘制位移S与转角δ的关系曲线S-δ曲线。
2)根据S-δ曲线、凸轮基园半径和正偏距,绘制凸轮的轮廓曲线。
000000凸轮仅用了0度,90度,150度,180度,300度几个点绘制轮廓曲线,同学们绘制时英多用些点(一般取12个点,再勾画轮廓曲线)第二篇:机械原理_凸轮机构设计机械原理课程设计——凸轮机构设计(一)目录 (1)_________________________(一)、题目及原始数据 (2)(二)、推杆运动规律及凸轮廓线方程 (3)(三)、(四)、(五)、(六)、(七)、(八)、计算程序方框图..........................5 计算源程序..............................6 程序计算结果及分析......................10 凸轮机构图..............................15 心得体会................................16 参考书. (16)(一)、题目及原始数据试用计算机辅助设计完成偏置直动滚子推杆盘形凸轮机构的设计,凸轮以1rad/s的角速度沿逆时针方向转动。
要求:(1)、推程运动规律为等加速等减速运动,回程运动规律为五次多项式运动规律;(2)、打印出原始数据;(3)、打印出理论轮廓和实际轮廓的坐标值;(4)、打印出推程和回程的最大压力角,以及出现最大压力角时凸轮的相应转角;(5)、打印出凸轮实际轮廓曲线的最小曲率半径,以及相应的凸轮转角;(6)、打印出凸轮运动的位移;(7)、打印最后所确定的凸轮的基圆半径。

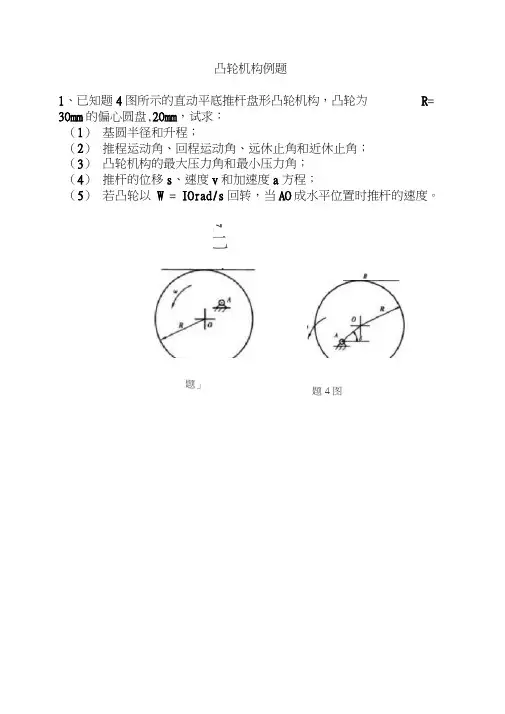
凸轮机构例题1、已知题4图所示的直动平底推杆盘形凸轮机构,凸轮为R= 30mm的偏心圆盘,20mm,试求:(1)基圆半径和升程;(2)推程运动角、回程运动角、远休止角和近休止角;(3)凸轮机构的最大压力角和最小压力角;(4)推杆的位移s、速度v和加速度a方程;(5)若凸轮以W = IOrad/s回转,当AO成水平位置时推杆的速度。
7匕题」图题4图解1、解:⑴ x0 = 10 = 2AO= 40mnit⑺ 推程J药角心=lS(r ,回程运动角<5;=180° 1近休止角九=0° ,远休止角玄a才-⑶由于平底垂盲于导路的平底推杆凸轮机构的圧力甫恒等于零,所以弧二%0U)如團所示,取旦唯钱与水平线的夹角肯凸轮的转角G M:推杆的位務右程再5 = x3+x3sh^-20(145b^推杆的速度方程対V =20&JCOS^推杆的加速度肓程为口一2%%航<5)当也=1[|曲创池碇于水平位貫时,5M}°或顷° ,所以推杆的速度为v= (20X LOcasS) mm.?«±20Uiiitn/82、10图所示对心直动尖顶推杆盘形凸轮机构中,凸轮为一偏心圆,O为凸轮的几何中心,O i为凸轮的回转中心。
直线AC与BD垂直,且Q试计算:=30tnnb(1)该凸轮机构中B、D两点的压力角;(2)该凸轮机构推杆的行程h。
⑴由區可加.氷口两掠的巫和闻次)母沖== arct吕[OQ# OB =arctgO. 5 = 25.565°(2) IT S h = = (2 > 30)mir = GG ITJTI3.如题13图所示的凸轮机构,设凸轮逆时针转动。
要求:画出凸轮的基圆半径,在图示位置时推杆的位移推杆开始上升时总=0°,以及传动角y题H團解s,凸轮转角厲(设。

凸轮推杆的运动规律可以通过一些例题来理解和掌握。
以下是一个关于凸轮推杆升程的例题:
例题:已知一偏置直动尖顶推杆盘形凸轮机构,其基圆半径为10mm,凸轮转速为10 r/min,要求推杆做一次往返运动,求推杆的升程和降程。
解:根据题目,凸轮转速为10 r/min,所以每分钟转过的角度为360°×10 = 3600°。
推杆做一次往返运动,即完成一个周期,需要转过的角度为360°。
因此,推杆完成一个周期所需的时间为3600°/ 360°= 10 min。
推杆的升程和降程可以根据基圆半径和推杆长度计算得出。
假设推杆长度为L,则升程为L -基圆半径,降程为L + 基圆半径。
根据题目,基圆半径为10mm,假设推杆长度L = 30mm,则推杆的升程和降程分别为20mm和40mm。
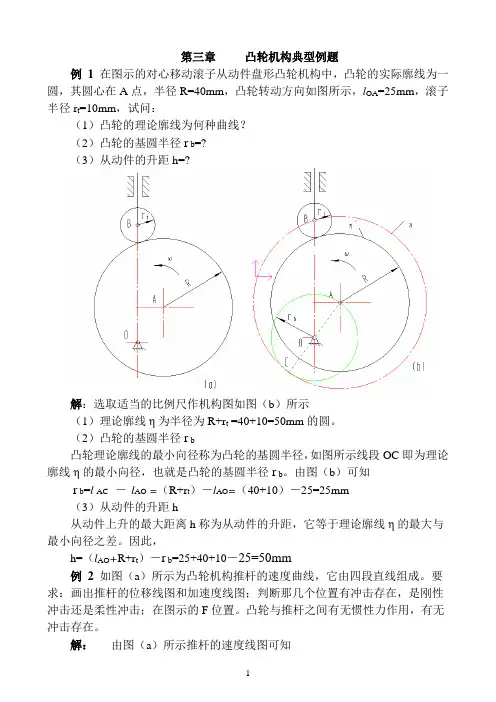
第三章凸轮机构典型例题例 1 在图示的对心移动滚子从动件盘形凸轮机构中,凸轮的实际廓线为一圆,其圆心在A点,半径R=40mm,凸轮转动方向如图所示,l OA=25mm,滚子半径r t=10mm,试问:(1)凸轮的理论廓线为何种曲线?(2)凸轮的基圆半径r b=?(3)从动件的升距h=?解:选取适当的比例尺作机构图如图(b)所示(1)理论廓线η为半径为R+r t =40+10=50mm的圆。
(2)凸轮的基圆半径r b凸轮理论廓线的最小向径称为凸轮的基圆半径,如图所示线段OC即为理论廓线η的最小向径,也就是凸轮的基圆半径r b。
由图(b)可知r b=l AC-l AO =(R+r t)-l AO=(40+10)-25=25mm(3)从动件的升距h从动件上升的最大距离h称为从动件的升距,它等于理论廓线η的最大与最小向径之差。
因此,h=(l AO+R+r t)-r b=25+40+10-25=50mm例 2 如图(a)所示为凸轮机构推杆的速度曲线,它由四段直线组成。
要求:画出推杆的位移线图和加速度线图;判断那几个位置有冲击存在,是刚性冲击还是柔性冲击;在图示的F位置。
凸轮与推杆之间有无惯性力作用,有无冲击存在。
解:由图(a)所示推杆的速度线图可知在OA段内,因推杆的速度v=0,故此段为推杆的近休止,推杆的位移及加速度均为零,即s=0,a=0,如图(b)(c)所示。
在AD段内,因v>0,故为推杆的推程段。
且在AB段内,因速度线图为上升的斜直线,故推杆先等加速上升,位移线图为抛物线运动曲线,而加速度线图为正的水平直线段;在BC线段内,速度线图为水平直线段,故推杆继续等速上升,位移线图为上升的斜直线,而加速度线图为与δ轴重合的线段;在CD 段内,因速度线图为下降的斜直线,故推杆继续等减速上升,位移线图为抛物线运动曲线,而加速度线图为负的水平直线段。
做出推杆的推程段的位移及加速度线图,如图(b)(c)所示。
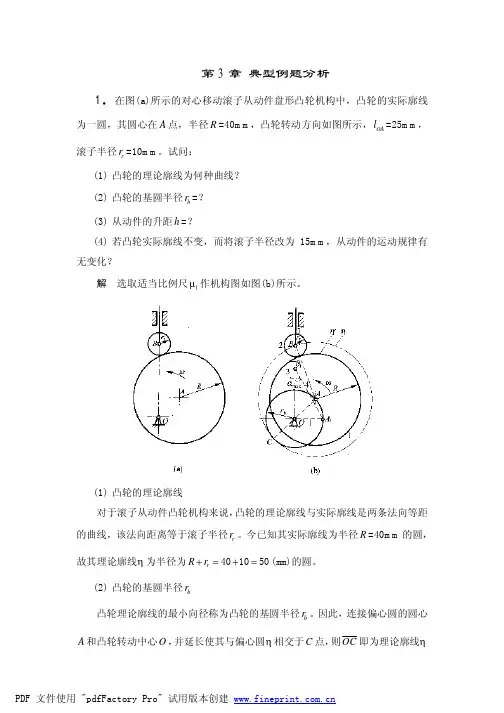
第3章 典型例题分析1.在图(a)所示的对心移动滚子从动件盘形凸轮机构中,凸轮的实际廓线为一圆,其圆心在A 点,半径R =40mm ,凸轮转动方向如图所示,OA l =25mm ,滚子半径r r =10mm 。
试问:(1) 凸轮的理论廓线为何种曲线?(2) 凸轮的基圆半径b r =?(3) 从动件的升距h =?(4) 若凸轮实际廓线不变,而将滚子半径改为15mm ,从动件的运动规律有无变化?解 选取适当比例尺l µ作机构图如图(b)所示。
(1) 凸轮的理论廓线对于滚子从动件凸轮机构来说,凸轮的理论廓线与实际廓线是两条法向等距的曲线,该法向距离等于滚子半径r r 。
今已知其实际廓线为半径R =40mm 的圆,故其理论廓线η为半径为401050r R r +=+=(mm)的圆。
(2) 凸轮的基圆半径b r凸轮理论廓线的最小向径称为凸轮的基圆半径b r 。
因此,连接偏心圆的圆心A 和凸轮转动中心O ,并延长使其与偏心圆η相交于C 点,则OC 即为理论廓线η的最小向径,它即为凸轮的基圆半径b r 。
由图(b)可知()(4010)2525b AC AO AO r l l R r l =−=+−=+−=(mm)(3) 从动件的升距h从动件上升的最大距离h 称为从动件的升距,它等于理论廓线η的最大和最小向径之差。
因此,()2540102550OA r b h l R r r =++−=++−=(mm)(4) 滚子半径改为15mm 后从动件的运动规律当凸轮的实际廓线η′保持不变,而将滚子半径r r 由10mm 增大至15mm 后,连杆长度AB l 将随之由50mm 增至55mm ,因此从动件将随之变化。
若希望从动件3的运动规律保持不变,正确的做法是让理论廓线η保持不变,作该理论廓线的法向等距离曲线,并使之距离等于15mm ,得到新的实际廓线。
2.某技术人员欲设计一台打包机,其推送包装物品的机构如图1所示。

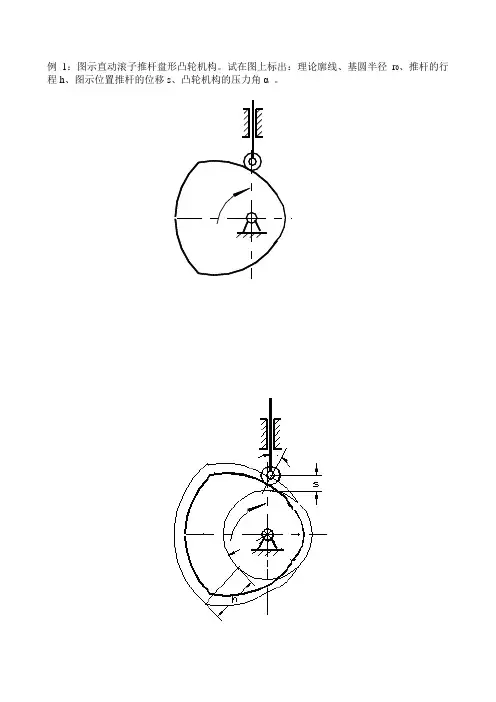
例1:图示直动滚子推杆盘形凸轮机构。
试在图上标出:理论廓线、基圆半径r0、推杆的行程h、图示位置推杆的位移s、凸轮机构的压力角α。
例2:图示对心直动滚子从动件盘形凸轮机构,凸轮是以A点为圆心的圆盘,O点为其回转中心。
试在图上标出:理论廓线、基圆半径r0、推杆的行程h、图示位置推杆的位移s、凸轮转过90°时机构的压力角 。
例3 已知一滚子移动从动件盘形凸轮轮廓如图所示。
试用图解法求出:
1.标出基圆。
2.凸轮由图示位置转到滚子与凸轮轮廓在B1'点接触时,所对应的凸轮转角φ1。
3.当滚子中心位于B2点时,凸轮机构的压力角α2、S。
例4:一滚子摆动从动件盘形凸轮的部分轮廓如图所示。
试用图解法求出:
1.滚子与凸轮轮廓由在D1点接触到在D2点接触的过程中,相应的凸轮转角φ12;
2.滚子与凸轮轮廓在D2点接触时凸轮机构的压力角α2。
凸轮一、单项选择题(从给出的A、B、C、D中选一个答案)1 与连杆机构相比,凸轮机构最大的缺点是。
A.惯性力难以平衡B.点、线接触,易磨损C.设计较为复杂D.不能实现间歇运动2 与其他机构相比,凸轮机构最大的优点是。
A.可实现各种预期的运动规律B.便于润滑C.制造方便,易获得较高的精度D.从动件的行程可较大3 盘形凸轮机构的压力角恒等于常数。
A.摆动尖顶推杆B.直动滚子推杆C.摆动平底推杆D.摆动滚子推杆4 对于直动推杆盘形凸轮机构来讲,在其他条件相同的情况下,偏置直动推杆与对心直动推杆相比,两者在推程段最大压力角的关系为关系。
A.偏置比对心大B.对心比偏置大C.一样大D.不一定5 下述几种运动规律中,既不会产生柔性冲击也不会产生刚性冲击,可用于高速场合。
A.等速运动规律B.摆线运动规律(正弦加速度运动规律)C.等加速等减速运动规律D.简谐运动规律(余弦加速度运动规律)6 对心直动尖顶推杆盘形凸轮机构的推程压力角超过许用值时,可采用措施来解决。
A.增大基圆半径B.改用滚子推杆C.改变凸轮转向D.改为偏置直动尖顶推杆7.()从动杆的行程不能太大。
A. 盘形凸轮机构B. 移动凸轮机构C. 圆柱凸轮机构8.()对于较复杂的凸轮轮廓曲线,也能准确地获得所需要的运动规律。
A 尖顶式从动杆 B.滚子式从动杆 C. 平底式从动杆9.()可使从动杆得到较大的行程。
A. 盘形凸轮机构 B 移动凸轮机构 C. 圆柱凸轮机构10.()的摩擦阻力较小,传力能力大。
A 尖顶式从动杆 B. 滚子式从动杆 C 平底式从动杆11.()的磨损较小,适用于没有内凹槽凸轮轮廓曲线的高速凸轮机构。
A. 尖顶式从动杆B.滚子式从动杆C. 平底式从动杆12.计算凸轮机构从动杆行程的基础是()。
A 基圆 B. 转角 C 轮廓曲线13.凸轮轮廓曲线上各点的压力角是()。
A. 不变的B. 变化的14.凸轮压力角的大小与基圆半径的关系是()。
A 基圆半径越小,压力角偏小 B. 基圆半径越大,压力角偏小15.压力角增大时,对()。