数学物理方法习题

数学物理方法习题解答一、复变函数部分习题解答第一章习题解答1、证明Re z 在z 平面上处处不可导。

证明：令Re z u iv =+。

Re z x =，,0u x v ∴==。

1ux∂=∂，0v y ∂=∂，u v x y ∂∂≠∂∂。

于是u 与v 在z 平面上处处不满足C －R 条件， 所以Re z 在z 平面上处处不可导。

2、试证()2f z z=仅在原点有导数。

证明：令()f z u iv =+。

()22222,0f z z x y u x y v ==+ ∴ =+=。

2,2u u x y x y ∂∂= =∂∂。

v vx y∂∂ ==0 ∂∂。

所以除原点以外，,u v 不满足C －R 条件。

而,,u u v vx y x y∂∂∂∂ , ∂∂∂∂在原点连续，且满足C －R 条件，所以()f z 在原点可微。

()0000x x y y u v v u f i i x x y y ====⎛⎫∂∂∂∂⎛⎫'=+=-= ⎪ ⎪∂∂∂∂⎝⎭⎝⎭。

或：()()()2*000lim lim lim 0z z x y z f z x i y z∆→∆→∆=∆=∆'==∆=∆-∆=∆。

22***0*00limlim lim()0z z z z z z zzz z z z z z z z z=∆→∆→∆→+∆+∆+∆∆==+−−→∆∆∆。

【当0,i z z re θ≠∆=，*2i z e z θ-∆=∆与趋向有关，则上式中**1z zz z∆∆==∆∆】3、设333322()z 0()z=00x y i x y f z x y ⎧+++≠⎪=+⎨⎪⎩，证明()z f 在原点满足C －R 条件，但不可微。

证明：令()()(),,f z u x y iv x y =+，则()33222222,=00x y x y u x y x y x y ⎧-+≠⎪=+⎨+⎪⎩， 33222222(,)=00x y x y v x y x y x y ⎧++≠⎪=+⎨+⎪⎩。

2. 试解方程：()0,044>=+a a z44424400000,0,1,2,3,,,,i k iiz a a e z aek aez i i ππππωωωωω+=-=====--若令则1．计算：（1）iii i 524321-+-+ （2）y =（3）求复数2⎝⎭的实部u 和虚部v 、模r 与幅角θ(1) 原式=()()()123425310810529162525255i i i i i i +⋅+-⋅+-++=+=-+--（2） 332()102052(0,1,2,3,4)k i e k ππ+==原式(3)2223221cos sin cos sin ,3333212u v 1,2k ,k 0,1,2,23i i i e r ππππππθπ⎛⎫==+=+==-+ ⎪⎝⎭⎝⎭=-===+=±±原式所以：，3．试证下列函数在z 平面上解析,并分别求其导数.(1)()()y i y y ie y y y x e x x sin cos sin cos ++-3.()()()()()()()()cos sin ,cos sin ,cos sin cos ,sin sin cos ,cos sin sin sin ,cos sin cos ,,,x x x x x x x x u e x y y y v e y y x y ue x y y y e y x ue x y y y y y ve y y x y e y y x ve y y y x y yu v u v x y y x u v z f z u iv z u f z =-=+∂=-+∂∂=---∂∂=++∂∂=-+∂∂∂∂∂==-∂∂∂∂=+∂'=∂证明：所以：。

由于在平面上可微所以在平面上解析。

()()()cos sin cos cos sin sin .x x x x vi e x y y y e y i e y y x y e y x x∂+=-++++∂由下列条件求解析函数()iv u z f += (),1,22i i f xy y x u +-=+-=解：()()()()()()()222222222212,2,212,2,,,2112,22111,0,1,1,,221112.222u v x y v xy y x x y v u v y x y x x x x x c x y x f z x y xy i xy y x c f i i x y c c f z x y xy i xy x y ϕϕϕϕ∂∂==+∴=++∂∂∂∂∂''=+=-=-+∴=-=-+∂∂∂⎛⎫=-+++-+ ⎪⎝⎭=-+==+==⎛⎫=-++-++ ⎪⎝⎭而即所以由知带入上式，则则解析函数2. ()21,3,,.ii i i i i e ++试求()()(((()()()2(2)Ln 144(2)4ln32Ln32ln32ln1222Ln 21cos ln sin ,0,1,2,3cos(ln 3)sin(ln 3),0,1,2,i i k k i ii i k i i k i i k i k i k i ii ii eeeei k e e e e i k i eeeππππππππππππ⎛⎫⎛⎫+ ⎪⎪-+++⎝⎭⎝⎭-++-+-⎛⎫⎛⎫++-+ ⎪⎪⎝⎭⎝⎭+====+=±±====+=±±=== 解：()222,0,1,2,cos1sin1.k i i k e e e e i π⎛⎫ ⎪⎝⎭+=±±=⋅=+3. 计算 2,:122c dzc z z z =++⎰()2222220110,1,1,11,220,022z z z z i z i z c z z z c z z ++=++=+==-+=≤++≠=++解：时，而在内，故在内解析，故原式 1.计算221(1),21c z z dz c z z -+=-⎰： ()2221(2),21cz z dz c z z -+=-⎰：（1）212(21)=4 z i z z i ππ==-+解：原式 （2）2112(21)=2(41)6z z i z z i z i πππ=='=-+-=解：原式. 计算2sin()114,(1):1,(2):1,(3): 2.122c z dz c z c z c z z π+=-==-⎰其中1sin (1)sin 442.112c z z z z i i z z πππ=-⎡⎤-⎢⎥===⎢⎥+-⎢⎥⎣⎦⎰解：(1)原式1sin (1)sin 442.11c z z z z i i z z πππ=⎡⎤+⎢⎥===⎢⎥-+⎢⎥⎣⎦⎰(2)原式 12(3):2,1,11,.c z z z c c ===-以分别以为中心，为半径，做圆1222sinsin44.11c c z zdz dz i i i z z ππ=+=+=--⎰⎰原式 3、将下列函数按()1-z 的幂级数展开，并指明收敛范围。

《 数学物理方法 》试题（A 卷）说明：本试题共3页四大题，30小题。

1．z 为复数，则（ ）。

A ln z 没有意义；B ln z 为周期函数；C Ln z 为周期函数；D ln()ln z z -=-。

2．下列积分不为零的是（ ）。

A 0.51z dz z π=+⎰； B 20.51z dz z π=-⎰； C10.5z dzz π=+⎰； D211z dz z π=-⎰。

3．下列方程是波动方程的是（ ）。

A 2tt xx u a u f =+； B 2t xx u a u f =+；C 2t xx u a u =； D2tt x u a u =。

4．泛定方程2tt x u a u =要构成定解问题，则应有的初始条件个数为（ ）。

A 1个；B 2个；C 3个；D 4个。

5．二维拉普拉斯方程的定解问题是（ ）。

A 哥西问题； B 狄拉克问题； C 混合问题； D 狄里克雷问题。

6．一函数序列的序参量n趋于某值a时有()(,)()()n ax f n x dx x f x dx ϕϕ→−−−→⎰⎰则我们称（ ）。

A (,)f n x 收敛于()f x ；B (,)f n x 绝对收敛于()f x ；C (,)f n x 弱收敛于()f x ；D (,)f n x 条件收敛于()f x 。

7．傅里叶变换在物理学和信息学中能实现（ ）。

A 脉冲信号的高斯展宽；B 高斯信号压缩成脉冲信号；C 实空间信号的频谱分析；D 复频信号的单频滤波。

8．用分离变量法求解偏微分方程定解问题的一般步骤是（ ）。

A 分离变量 解单变量本征值问题 得单变量解得分离变量解； B 分离变量 得单变量解 解单变量本征值问题 得分离变量解； C 解单变量本征值问题 得单变量解 分离变量 得分离变量解； D 解单变量本征值问题 分离变量 得单变量解 得分离变量解。

9．下列表述中不正确的是（ ）。

A 3sin zz 在0z =处是二阶极点；B 某复变函数在开复平面内有有限个奇点，所有这些奇点的残数之和为零；C 残数定理表明，解析函数的围线积分为复数；D 某复变函数在某处为m 阶极点，则其倒函数在该奇点处为m 阶零点。

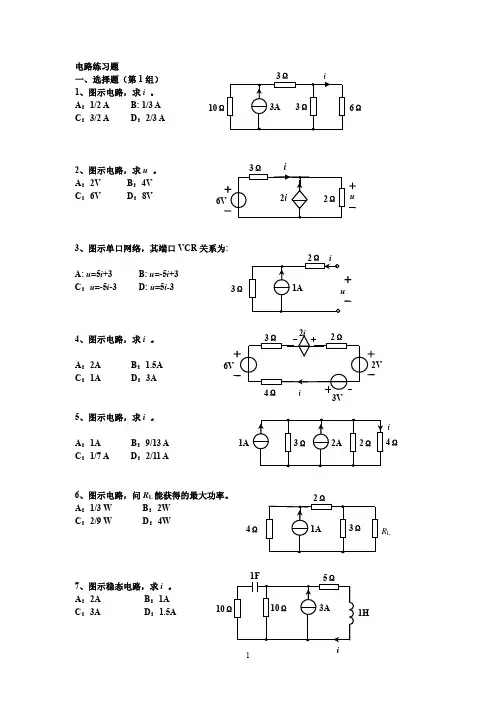
电路练习题一、选择题（第1组）1、图示电路，求i 。

A ：1/2 A B: 1/3 A C ：3/2 A D ：2/3 A2、图示电路，求u 。

A ：2VB ：4VC ：6VD ：8V3、图示单口网络，其端口VCR 关系为:A: u =5i +3 B: u =-5i +3 C ：u =-5i -3 D: u =5i-34、图示电路，求i 。

A ：2AB ：1.5AC ：1AD ：3A5、图示电路，求i 。

A ：1AB ：9/13 AC ：1/7 AD ：2/11 A6、图示电路，问R L 能获得的最大功率。

A ：1/3 W B ：2W C ：2/9 W D ：4W7、图示稳态电路，求i 。

A ：2A B ：1AC ：3AD ：1.5Ai 4ΩR L4Ω6Ω 10Ω1H108、图示稳态电路，问电容中的储能。

A ：4J B ：2JC ：8JD ：1J9、图示电路，t < 0时处于稳态, t = 0时，开关切到a ， 当t = 5s 时，u c (t )是多少？A ：6.3VB ：5VC ：2.4VD ：3.16V10、图示电路，t < 0时处于稳态，t = 0时， 开关断开，求t = 1s 时u c (t )是多少？ A ：1.47V B ：2.94V C: 5V D ：4V11、图示电路原处于稳态，在t = 0时， 开关断开，求t = 0.1s 时的电流i (t )。

A ：1A B ：0 C ：0.358A D ：0.184 A12、图示正弦稳态电路，求i (t ) 。

A ：)452cos(2°+t A B ：)452cos(2°−t A C ：)452cos(2°−t A D ：)452cos(2°+t A13、图示正弦稳态电路中，有效值： I 是10A ，I R 是8A 。

问I c 是多少？ A ：2A B ：18A C ：6A D ：4Ai(t)1H0.5Ω2ΩA2cos 22t u c1A c (t)2A14、图示正弦稳态电路， 求电阻上的平均功率。

数学物理方法期末考试试题# 数学物理方法期末考试试题## 第一部分：选择题（每题2分，共20分）1. 以下哪个不是数学物理中的常用方法？A. 傅里叶变换B. 拉普拉斯变换C. 泰勒级数展开D. 牛顿迭代法2. 求解偏微分方程时，分离变量法的基本思想是什么？A. 将偏微分方程转化为常微分方程B. 将偏微分方程分解为几个独立的方程C. 将偏微分方程转化为线性方程D. 将偏微分方程转化为积分方程3. 在数学物理中，格林函数通常用于解决什么问题？A. 线性代数问题B. 非线性偏微分方程C. 边界值问题D. 初始值问题4. 以下哪个是求解波动方程的典型方法？A. 特征线法B. 有限差分法C. 有限元法D. 蒙特卡洛方法5. 拉普拉斯方程在数学物理中通常描述了什么类型的物理现象？A. 波动现象B. 热传导现象C. 流体动力学问题D. 电磁场问题## 第二部分：简答题（每题10分，共30分）6. 简述傅里叶变换在数学物理中的应用。

7. 解释什么是边界层理论，并说明它在流体力学中的重要性。

8. 描述格林函数在求解偏微分方程中的作用。

## 第三部分：计算题（每题25分，共50分）9. 给定函数 \( f(x) = x^2 - 4x + 3 \)，使用泰勒级数展开在\( x = 1 \) 处展开 \( f(x) \) 并求出展开式。

10. 考虑一个无限长直导体，在 \( x \) 轴上，导体的电势 \( V(x) \) 满足泊松方程 \( \nabla^2 V = -\rho/\varepsilon_0 \)，其中\( \rho \) 是电荷密度，\( \varepsilon_0 \) 是真空电容率。

假设\( \rho \) 是常数，求解 \( V(x) \)。

## 第四部分：论述题（共30分）11. 论述数学物理方法在解决实际物理问题中的应用，并给出至少两个具体的例子。

请注意，以上内容仅为示例，实际的数学物理方法期末考试试题可能会包含不同的问题和要求。

数学物理方法试卷数学物理方法是一门重要的学科，它将数学和物理学相结合，以求解物理问题为目标。

本文档旨在提供一份针对数学物理方法的试卷，帮助学生加深对该学科的理解和应用能力。

一、选择题（共10题，每题2分）1. 下列哪个是四位数？A. 123B. 12345C. 123456D. 12342. 如何计算三角形的面积？A. 底乘高除以2B. 长乘宽C. 半径的平方乘以πD. 无法计算3. 下列哪个是速度的单位？A. 米/秒B. 千克C. 焦耳D. 牛顿4. 什么是牛顿第三定律？A. 物体的加速度和作用力成正比B. 物体的质量和加速度成正比C. 在力的作用下，物体会产生加速度D. 任何作用力都有一个相等且方向相反的反作用力5. 单位矩阵是什么？A. 所有元素都为1的矩阵B. 所有元素都为0的矩阵C. 对角线上元素都为1，其他元素为0的矩阵D. 所有元素都相等的矩阵6. 下列哪个是圆的面积公式？A. πr^2B. 2πrC. πd^2D. 0.5πr^27. 加速度的单位是什么？A. 米/秒^2B. 米/秒C. 十米/秒^2D. 千米/小时8. 下列哪个公式用于计算动能？A. F = maB. W = FdC. E = mc^2D. KE = 1/2mv^29. 如何计算两个向量的点积？A. 向量相乘再求和B. 向量相除C. 向量相减D. 无法计算10. 下列哪个没被广义相对论所解释？A. 引力B. 黑洞C. 宇宙膨胀D. 电磁力二、解答题（共3题，每题10分）1. 请用泰勒级数展开sin(x)，并计算在x=π/6时的近似值。

2. 请用微分方程求解y'' + 4y = 0，并给出其特解。

3. 请解释质心是什么，并说明为什么在某些问题中质心坐标系非常有用。

本试卷针对数学物理方法的知识进行了全面的考察。

选择题部分测试了学生的基础知识和概念理解能力，而解答题则要求学生能够运用所学的数学物理方法进行实际问题的求解和解释。