小波变换第五次作业分析解析
- 格式:doc
- 大小:430.71 KB
- 文档页数:8

小波变换分析范文小波变换是一种信号分析技术,可以将信号表示为时频域上的函数。
相比于傅里叶变换,小波变换在时域和频域上都具有更好的局部性和分辨率,能够更好地描述非平稳信号。
本文将从小波变换的基本原理、算法和应用领域等方面进行分析。
一、基本原理小波变换是一种多尺度分析方法,其基本思想是将信号分解成一组基函数(小波基),然后通过对这些基函数与信号的内积运算得到信号在不同尺度上的时频表示。
小波基具有一些特殊的数学特性,如正交性、紧支性和可调节的带宽等,这使得小波变换能够更好地揭示信号的时频信息。
小波变换可以通过离散小波变换(DWT)和连续小波变换(CWT)来实现。
1.离散小波变换(DWT)离散小波变换将信号分解成不同频率域和尺度域的小波基函数,并通过滤波和下采样操作实现。
具体步骤如下:a.将信号通过低通滤波器和高通滤波器分解为近似系数和细节系数;b.对近似系数进一步进行低通滤波和高通滤波,得到第二层的近似系数和细节系数;c.反复重复上述步骤,直到达到所需的尺度。
2.连续小波变换(CWT)连续小波变换通过将信号与不同尺度和位置上的小波基函数进行内积运算来表示信号的时频信息。
具体步骤如下:a.选取一个母小波函数作为基函数;b.将母小波函数进行尺度变换和平移变换,得到一组具有不同尺度和位置的小波基函数;c.将信号与这组小波基函数进行内积运算,得到信号在不同尺度和位置上的时频表示。
小波变换具有多尺度分析能力,可以在不同尺度上观察信号的局部细节特征,并且能够有效地提取信号的边缘、脉冲和突变等特征。
二、常见小波变换算法1.傅里叶变换转换尺度(FBS)小波变换FBS小波变换是比较基础的小波变换算法,通过将傅里叶变换应用于尺度变换的细节部分,将信号分解成自由基函数的线性组合。
2.快速小波变换(FWT)FWT是一种高效的小波变换算法,可以在O(N)的时间复杂度内实现小波变换。
FWT通过迭代地应用滤波器组合和下采样操作来实现信号的分解和重构。

小波变换完美通俗解读
嘿,朋友们!今天咱就来好好唠唠这小波变换!这玩意儿可神奇啦!
你看啊,就好比我们听音乐。
那音乐里有各种不同的声音吧,高音、低音啥的。
小波变换呢,就像是一个超级厉害的音乐分析师,能把这音乐里的各种成分给分得清清楚楚!比如我们平时说话的声音,有高有低,语调也不一样,小波变换就能把这些不同的部分准确地分辨出来。
再想想看,我们看一幅画,上面有各种色彩和线条。
小波变换就像是一个能把这些元素都拆解开来的大师!它可以把画里的细节,什么线条的走向啦,颜色的分布啦,都弄得明明白白。
那这小波变换到底有啥牛的呢?嘿,你想啊,我们在生活中,有时候会遇到很复杂的信息,就像一团乱麻。
而小波变换就能像一把神奇的剪刀,把这团乱麻给理清咯!
比如说医生要看 X 光片,那么多复杂的影像,小波变换就能帮忙找出关键的地方,难道这还不厉害吗?或者是在气象研究中,那么多变幻莫测的气候数据,小波变换就能从中找出规律!你说神不神奇!
“哎呀,那这小波变换也太了不起了吧!”这时候可能有人就问了,“那咱普通人能用它干啥呀?”嘿,用处可大了去了!如果你喜欢摄影,它可以帮你更好地处理照片,让照片更清晰更漂亮。
要是你对声音处理感兴趣,它能让你的音乐听起来更棒!这不就是让我们的生活变得更美好嘛!
总之,小波变换真的是一个超级神奇又超级实用的东西!大家可得好好去了解了解它,说不定就能给你的生活带来意想不到的惊喜呢!别小瞧它哦,它真的超厉害!。


小波分析小结(小编整理)第一篇:小波分析小结小波分析的形成小波分析是一门数学分支,是继Fourier变换之后新的时频域分析工具。
小波理论的形成经历了三个发展阶段:Fourier变换阶段:Fourier变换是将信号在整个时间轴上进行积分,它将信号的时域特征和频域特征联系起来,分别进行分析。
设信号f(t),其Fourier变换为:F(ω)=⎰f(t)e-iωtdt-∞∞F(ω)确定了f(t)在整个时间域上的频谱特性。
但Fourier变换不能对信号从时域和频域结合起来分析,它是一种全局变换,在时间域上没有任何分辨率。
例:f(t)=1,(-2<=t<=2),其Fourier变换对应图如下:短时Fourier变换阶段:短时Fourier变换即加窗Fourier变换,其思想是把信号分成许多小的时间间隔,用Fourier分析每个时间间隔,以确定该间隔存在的频率,达到时频局部化目的。
其表达式为:Gf(ω,τ)=〈f(t),g(t-τ)ejωt〉=⎰f(t)g(t-τ)e-jωtdtR式中,g(t)为时限函数,即窗口函数,e-jωt起频限作用,Gf(ω,τ)大致反映了f(t)在τ时、频率为ω的信号成分含量。
由上式,短时Fourier变换能实现一定程度上的时频局部化,但窗口函数确定时,窗口大小和形状固定,所得时频分辨率单一。
小波分析阶段:为了克服上述缺点,小波变换应运而生。
小波变换在研究信号的低频成分时其窗函数在时间窗长度上增加,即在频率宽上减小;在研究信号的高频成分时其窗函数在时间窗长度上减小,而在频率宽上增加。
对信号可以进行概貌和细节上的分析。
小波的定义:∝(ω),若满足设ψ(t)∈L2(R)(为能量有限的空间信号),其Fourier变换为ψ容许条件:|ψ(ω)|2⎰-∞|ω|dω<+∞∞∝∝(0)=∞ψ(t)dt=0,说明ψ(t)具有波动则称ψ(t)为母小波,由容许条件可得:ψ⎰-∞性,在有限区间外恒为0或快速趋近于0.t-12以Marr小波ψ(t)=(1-t)e2为例,如下图:2π2将母小波进行伸缩平移所得小波系列称为子小波,定义式如下:ψb,a(t)=1t-bψ(),a>0aa其中a为伸缩因子,b为平移因子。


小波变换分析范文小波变换(Wavelet Transform,WT)是一种时频分析方法,对信号进行多尺度分析。
它与傅里叶变换不同,不仅能够提供频域信息,还能够提供时间信息。
小波变换能够在不同时间尺度下分析信号的频率成分,具有很强的局部性和稳定性。
本文将介绍小波变换的原理、应用场景和相关算法。
小波变换的基本原理是将信号与一组小波基函数进行卷积计算,通过改变小波基函数的尺度和形状,可以实现对不同频率成分的局部分析。
小波基函数是一组局部化函数,具有有限持续性,且没有周期性,因此能够更好地适应信号的局部特征。
小波基函数常用的有哈尔小波、Daubechies 小波、Morlet小波等。
小波变换相比傅里叶变换具有以下优势:1.时间和频率的局部性:小波变换能够同时提供时间和频率信息,可以更准确地描述信号的瞬态特征。
傅里叶变换将信号映射到频域,无法提供时间信息,而小波变换通过改变小波基函数的尺度,可以在不同时间尺度下分析信号的频率成分。
2.多尺度分析:小波变换是一种多尺度分析方法,通过改变小波基函数的尺度,可以对信号的不同频率成分进行分析。
傅里叶变换只能提供全局频率信息,无法区分不同频率的瞬态成分。
3.离散性:小波变换可以对离散信号进行处理,能够在有限的时间和频率分辨率内对信号进行分析。
傅里叶变换是对连续信号进行处理的,需要对信号进行采样和插值,会引入采样和重建误差。
小波变换在信号处理领域有广泛的应用,包括图像压缩、信号降噪、语音识别、地震勘探等。
其中,小波变换在图像压缩中的应用较为广泛。
传统的图像压缩方法如JPEG采用离散余弦变换(DCT),但其对图像的瞬态特征不敏感。
而小波变换能够更好地提取图像的局部特征,可以实现更高的压缩比和更好的重构质量。
小波变换的具体实现有多种算法,包括离散小波变换(DWT)、连续小波变换(CWT)和快速小波变换(FWT)等。
离散小波变换是最常用的小波变换算法,通过一系列卷积和下采样操作实现小波系数的计算。

基于小波变换的人脸识别近年来,小波变换在科技界备受重视,不仅形成了一个新的数学分支,而且被广泛地应用于模式识别、信号处理、语音识别与合成、图像处理、计算机视觉等工程技术领域。
小波变换具有良好的时频域局部化特性,且其可通过对高频成分采取逐步精细的时域取样步长,从而达到聚焦对象任意细节的目的,这一特性被称为小波变换的“变聚焦”特性,小波变换也因此被人们冠以“数学显微镜”的美誉。
具体到人脸识别方面,小波变换能够将人脸图像分解成具有不同分辨率、频率特征以及不同方向特性的一系列子带信号,从而更好地实现不同分辨率的人脸图像特征提取。
4.1 小波变换的研究背景法国数学家傅立叶于1807年提出了著名的傅立叶变换,第一次引入“频率”的概念。
傅立叶变换用信号的频谱特性来研究和表示信号的时频特性,通过将复杂的时间信号转换到频率域中,使很多在时域中模糊不清的问题,在频域中一目了然。
在早期的信号处理领域,傅立叶变换具有重要的影响和地位。
定义信号(t)f 为在(-∞,+∞)内绝对可积的一个连续函数,则(t)f 的傅立叶变换定义如下:()()dt e t f F t j ωω-⎰∞-∞+= (4-1) 傅立叶变换的逆变换为:()()ωωπωd e F t f t j ⎰+∞∞-=21 (4-2)从上面两个式子可以看出,式(4-1)通过无限的时间量来实现对单个频率的频谱计算,该式表明()F ω这一频域过程的任一频率的值都是由整个时间域上的量所决定的。
可见,式(4-1)和(4-2)只是同一能量信号的两种不同表现形式。
尽管傅立叶变换可以关联信号的时频特征,从而分别从时域和频域对信号进行分析,但却无法将两者有效地结合起来,因此傅立叶变换在信号的局部化分析方面存在严重不足。
但在许多实际应用中,如地震信号分析、核医学图像信号分析等,研究者们往往需要了解某个局部时段上出现了哪个频率,或是某个频率出现在哪个时段上,即信号的时频局部化特征,傅立叶变换对于此类分析无能为力。

科研训练报告一:科研训练目标及意义在深入理解经典Fourier 变换的基础上,通过系统介绍加窗Fourier 变换(Windowed Fourier Transfrom, WFT ),小波变换(Wavelet trsnaform,WT )等定义,理解时间分辨率,频率分辨率及,时频局部化性质等基本概念;通过编程实现基本的时频分析方法,理解时变信号中时频结构信息。
二:科研训练任务1.理解加窗Fourier 变换的意义2.编程实现加窗Fourier 分析几种合成信号3.利用加窗Fourier(小波变换)分析几种典型的合成信号4.观察分析窗函数,窗长变化,频率,分辨率的影响5.可尝试利用加窗Fourier (小波变换)正变换分析实测语音等信号三:报告结构四:加窗Fourier 分析 v.1.Fourier 正变换v.1.a 离散Fourier 正变换数学描述有限长序列通过离散傅里叶变换,并通过快速傅里叶变换算法FFT 即得:X (k )=∑x (j )W ℵ(j−1)(R−1)ℵj=1其中:W ℵ=e −2∗π∗j/N v.1.b.Fourier 正变换Matlab 实现 被分析信号为N 维列向量;x =[x (0),x (1),x (2),x (3)⋯x (n −1)]T变换因子为:[W 0⋯W 0⋮⋱⋮W 0⋯W(N−1)(N−1)] DFT 结果为X =[X (0),X (1),X (2),X (3)⋯X (n −1)]T以矩阵形式表示DFT : X N =W N x N (具体代码参见代码code erst ) v.1.c.Fourier 正变案例分析总结 step1 检测代码的正确性当输入一个离散的冲激函数的Delta 函数,其DFT 变换的幅度谱为一等幅,幅度为1的白色谱。
(参见图a.3.1) Step2 分析信号特性当输入一个正弦函数时,运行结果如下:幅度谱为一对称的离散冲激信号,冲激的横坐标为其频率,纵坐标为其幅度。

小波变换中的常见问题解答与技巧分享小波变换是一种在信号处理中广泛应用的数学工具,它可以将信号分解成不同频率的成分,并且能够提供时间和频率的局部信息。
然而,对于初学者来说,小波变换可能会带来一些困惑和挑战。
本文将解答一些常见问题,并分享一些小波变换的技巧,帮助读者更好地理解和应用小波变换。
一、什么是小波变换?小波变换是一种将信号分解成不同频率的成分的数学工具。
它使用一组称为小波基函数的函数来表示信号。
这些小波基函数具有不同的频率和时间定位特性,可以提供信号在时间和频率上的局部信息。
二、为什么要使用小波变换?小波变换具有许多优点,使其在信号处理中得到广泛应用。
首先,小波变换可以提供信号在时间和频率上的局部信息,而傅里叶变换只能提供全局信息。
其次,小波变换可以在不同尺度上对信号进行分解,从而能够捕捉到信号的细节和变化。
此外,小波变换还可以用于信号去噪、特征提取、压缩等方面的应用。
三、小波变换的基本步骤是什么?小波变换的基本步骤包括选择合适的小波基函数、进行小波变换、对小波系数进行阈值处理、进行逆小波变换。
首先,需要根据信号的特点选择合适的小波基函数,常用的有Haar小波、Daubechies小波等。
然后,将信号与选定的小波基函数进行卷积运算,得到小波系数。
接下来,可以对小波系数进行阈值处理,去除噪声或不重要的细节信息。
最后,进行逆小波变换,将处理后的小波系数重构成信号。
四、如何选择合适的小波基函数?选择合适的小波基函数是小波变换中的关键步骤。
不同的小波基函数适用于不同类型的信号。
一般来说,Haar小波适用于具有突变特性的信号,而Daubechies小波适用于平滑或趋势型的信号。
此外,还有一些其他类型的小波基函数,如Symlet小波、Coiflet小波等,可以根据信号的特点选择合适的小波基函数。
五、小波变换有哪些应用?小波变换在信号处理中有广泛的应用。
其中,最常见的应用之一是信号去噪。
小波变换可以将信号分解成不同频率的成分,通过对小波系数进行阈值处理,可以去除信号中的噪声。
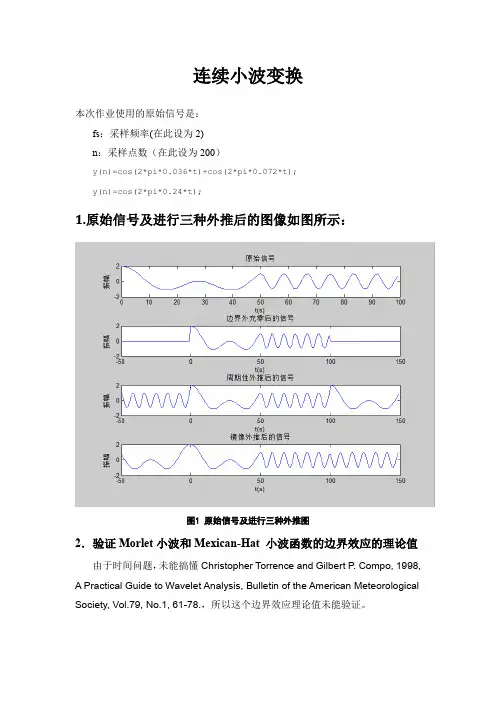
连续小波变换本次作业使用的原始信号是:fs:采样频率(在此设为2)n:采样点数(在此设为200)y(n)=cos(2*pi*0.036*t)+cos(2*pi*0.072*t);y(n)=cos(2*pi*0.24*t);1.原始信号及进行三种外推后的图像如图所示:图1 原始信号及进行三种外推图2.验证Morlet小波和Mexican-Hat 小波函数的边界效应的理论值由于时间问题,未能搞懂Christopher Torrence and Gilbert P. Compo, 1998, A Practical Guide to Wavelet Analysis, Bulletin of the American Meteorological Society, Vol.79, No.1, 61-78.,所以这个边界效应理论值未能验证。
3.试验边界外充零、周期性外推、镜像外推的优劣3.1原始数据作小波变换图2 Mexican Hat小波变换和Morlet小波的变换从图2可以看出:(1)Mexican Hat小波变换在相同的尺度下有更好的时间分辨率;(2)尺度的大小表示小波的宽窄,尺度大,表示小波比较宽,频率就较低;相反,尺度小则表示频率高;而且在经过小波变换后的边界影像范围随尺度的增大而变宽;3.2充零外推后的小波变换:图3 充零外推后的小波变换3.3周期延拓的小波变换:图4 周期延拓的小波变换3.4镜像外推的小波变换:图5 镜像外推的小波变换3.5综合3.2-3.4,可得以下结论:(1)充零外推后的小波变换与原始信号直接小波变换基本上没有什么区别,保证了原始信号的边界效应,但是时间的不连续性可能会导致信号的高频信号的丢失;(2)周期延拓后的小波变换同样会造成时间的不连续性,导致信号的边界效应很明显;(3)镜像外推后的小波变换可以保证时间上的连续,理论上可以应用于各种信号,但仍要与实际相结合使用。
第10章 小波变换与JPEG 2000编码之小波变换虽然基于DCT 的JPEG 标准的压缩效果已经很不错,但在较高压缩比时会出现明显的马赛克现象,且不能渐进传输。
为了适应网络发展的需要,JPEG 于2000年底推出了采用DWT (Discrete Wavelet Transform 离散小波变换)的JPEG 2000标准。
小波变换是1980年代中期发展起来的一种时频分析方法,比DCT 这样的傅立叶变换的性能更优越,被广泛应用于调和分析、语音处理、图像分割、石油勘探和雷达探测等等方面,也被应用于音频、图像和视频的压缩编码。
本章先介绍小波变换的来龙去脉,然后分别介绍连续小波变换、离散小波变换、Haar 小波变换和整数小波变换,最后介绍JPEG 2000的编码算法和标准。
10.1 小波变换小波变换(wavelet transform)是傅立叶变换的发展,中间经历了窗口傅立叶变换。
原始数据一般是时间或空间信号,在时空上有最大分辨率。
时空信号经傅立叶变换后得到频率信号,在频域上有最大分辨率,但其本身并不包含时空定位信息。
窗口傅立叶变换通过对时空信号进行分段或分块进行时空-频谱分析,但由于其窗口的大小是固定的,不适用于频率波动大的非平稳信号。
而小波变换可以根据频率的高低自动调节窗口大小,是一种自适应的时频分析方法,具有多分辨分析功能。
本节先讨论小波变换与(窗口)傅立叶变换的关系,然后依次介绍连续小波变换、离散小波变换、Haar 小波变换和第二代小波变换(整数小波变换)。
10.1.1 傅立叶变换与小波变换傅立叶变换(Fourier transform)是法国科学家Joseph Fourier 发表于1822年的他在用无穷三角级数求解热传导偏微分方程时所提出的一种数学方法,它可将时空信号变换成频率信号。
鉴于傅立叶变换不含时空定位信息,(1971年的诺贝尔物理学奖获得者)匈牙利人Dennis Gabor 于1946年提出窗口傅立叶变换(window Fourier transform )。
小波变换作业小波转换在分析化学中的应用摘要:小波变换是80年带发展起来的一种新的数学分支,因为小波变换具有许多其他信号出路方法所不具备的优良特征,如可变的时频分辨率和可调节的局部支持等,所以使它成为信号处理的一种强有力的工具。
本文介绍了小波分析的发展,现状和它在分析化学中的应用,对其可能运用的领域进行了探讨。
关键词:小波:信号;傅立叶变换;分析化学Abstract: Because of the fine properties of flexible time---frequency windows and governedlocalized support, the wavelet transform is a useful tool in signal processing. The text introduced the development and present of Wavelet Analysis. A review of application of Wavelet Analysis in Analytical Chemistry has been presented.Key words: wavelet; signals; Fourier Transform; analytical chemistry小波(又叫子波 )变换的理论是最近发展起来的新的数学方法, 被认为是傅里叶分析理论的重大突破。
小波变换同时在时域和频域中具有较好的局部特性, 将时频统一于一体来研究信号。
而傅里叶变换则与此不同, 它把信号完全变换到频域中研究, 对频率的分辨率是无穷, 但对时间的分辨率是零; 传统的时域分析则完全在时域中分析信号, 它对时间的分辨率是无穷, 但对频率的分辨率为零。
虽然加窗傅里叶变换能部分克服傅里叶变换的不足, 但其窗口大小固定不变, 在应用中也存在它的局限性。
小波变换则同时对时间和频率具有较好的分辨率, 目前已经在若干领域取得了突破性的成果。
研究生“小波变换”课程期末大作业2010/06/17说明:下述四道题中可任选两道一、结合MATLAB中的数据文件leleccum (1-D),研究小波去噪的原理和方法。
1.综述用小波去除噪声的原理。
包括:(1)去噪阈值的种类,各种阈值形成的原理,阈值风险函数;(2)阈值使用的方法;2.MATLAB 6.5中与1-D信号去噪相关的m 文件有14个,结合所给数据的去噪,讨论这些文件的应用;3.对上述数据实现去噪;参考文献:1.M Jansen, Noise Reduction by Wavelet Threshold, 2001.2. D L Donoho. De-noiseing by soft-thresholding. IEEE Tran on Info Theory 1995(见附件)请自己在EI 或IEEE全文库上给定相应的关键词,查找其他去噪相关文献。
二、研究利用小波变换检测信号中的奇异点及由模最大重建信号的原理与方法。
内容包括:1.信号中的突变点在小波变换中的行为;2.由模最大重建信号的原理与方法;3.下载ecg文件(见附件),用open_ecg打开该文件实现对该信号的峰值(R波)检测。
该信号的抽样频率为360Hz;4.令j=1~6, 试用各尺度下的模最大重建原信号;参考文献:1.S Mallat. Singularity Detection and Processing with Wavelet. IEEE Tran on IF, 1992(见附件)2.S Mallat. Signal Characterization from Multiscale Edges. 1990(见附件)请自己在EI 或IEEE全文库上给定相应的关键词,查找其他相关文献。
三、结合MATLAB W A VELET TOOLBOX 中有关小波包的文件(不包括两个2-D文件),研究:1.小波包最佳分解层(即尺度j)的选择原理;2.最佳小波包选择的原理;3.上述13个文件的功能及相关关系;4.利用MATLAB中的数据文件leleccum(1-D),按最佳分解层及最佳小波包进行分解。
地球科学学院小波分析课程作业课程名称:小波分析指导老师:学生姓名:学号:几种时频分析方法1 短时傅里叶变换为了研究信号在局部时间范围内的瞬时频率特性,1946年,D.GABOR 引进了短时傅氏变换或窗口傅氏变换的概念,其基本原理是取一个称为(t)g 窗口的函数,使它在有限的区间范围外恒等于零或趋于零。
设任意信号(t)f ,并假设该信号在一个以时间τ为中心,且范围有限的窗口函数)-(t τg 内是稳定的,这样,窗口内函数)-(t)g(t τf 的傅氏变换就定义为短时傅氏变换,表示为dt e T t i STFT ωτωτ--)-f(t)g(t ),(⎰∞∞=STFT 是通过滑动时窗来计算其频谱,因而它的时间分辨率和频率分辨率受Heisenberg 测不准原理约束。
因此利用短窗口有较高的时间分辨率,但是频率分辨率差。
2 小波变换常见的小波变换有连续、二进制以及离散小波变换等。
在连续小波变换中,仅要求小波函数满足容许条件即可,这使得在选择小波函数时具有很大的自由度。
对任意地震信号函数)((t)2R L f ∈,其连续小波变换定义为 )f(t)dt a b -t (a 1(t)f(t)dt b)(a,-*-b a,⎰⎰∞∞∞∞==ϕψw T 式中,a为尺度因子,b为平移参数,函数ψ(t)称为母小波。
小波分析具有可调的时频窗口,被广泛地应用于地震信号处理中,但是也存在着一定的局限性,主要表现在难以选择小波基、固定的基函数、恒定的多分辨率,信号的能量—时间—频率分布也很难定量给出。
3 S 变换为了解决短时傅氏变换只能以一种分辨率进行时频分析及小波变换不能直接与频率对应的缺陷,1996年美国地球物理学家Stockwell 在前人的基础上提出了S 变换。
S 变换中,基本小波是由简谐波与高斯函数的乘积构成的,基本小波中的简谐波在时间域仅作伸缩变换,而高斯函数则进行伸缩和平移。
这一点与连续小波变换不同,在连续小波变换中,简谐波与高斯函数进行同样的伸缩和平移。
小波变换第五次作业专业:信息与通信工程 学号:406130714098 姓名:徐标1. 设计一 CQMFB ,低通滤波器 ()0H z 来自一半带滤波器。
该半带滤波器的长度为47,通带截止频率0.42p ωπ=,试给出()0H z ,()0G z ,()1H z ,()0z G 的幅频响应,单位抽样响应。
2.产生一信号()x n ,它由两个正弦加白噪声组成,一个在低频,一个在高频,正弦的频率及与白噪声的信噪比自己给定。
试用所设计的滤波器组对该信号进行分解和重建。
比较重建后的效果。
设计思路:参照课本181页(1) 首先设计一个半带滤波器()LF H z ,N=47,p ω=0.42π。
根据第六章半带滤波器的设计思路,先要用Chebyshew 最佳一致逼近法设计一个单带滤波器G (z ),令其通带截止频率为2p ω=0.84π,s ωπ=,长度为2J=24。
由此单带滤波器,可得半带滤波器()LF H z =()()1/2212N G z z --⎡⎤+⎣⎦,可以通过时域对g (n )作二倍的插值,并令插值后的序列的中心点位0.5。
结果如下:(2)对半带滤波器()LF H z 进行处理,得到幅频响应非负的半带滤波器()P z 。
方法:令中间过度的滤波器:()()H jwjw LF LF eH e σ++=+,假定()LF H z 为零相位,实现上式的简单办法是令:()()()n 0,0LF LFLFh n h n h n n σ+≠⎧⎪=⎨+=⎪⎩,,再令()()0.5H 0.5LF P z z σ+=+,则()P z 是一个半带滤波器,()jw P e 是非负的。
产生半带滤波器()P z 的幅频响应:零极分析如图:由上面左图图可以看出,()P z 共有46对极零点,其中11个零点在单位圆内,11个零点在单位圆外,其余24个零点在单位圆上,对()P z 做谱分解,因为对于CQFMB 而言,谱分解的最佳选择是使()0H z 成为最小相位系统,取单位圆内的11个零点以及12个单位圆上的零点赋予()0H z ,从而构造出符合要求的()0H z ,并得到其幅频响应、单位抽样响应,同时,根据()()()()0101H z H z G z G z 之间的对应关系,很容易得到其他3个滤波器的幅频响应、单位抽样响应。
结果如下:()0jw H e 和()1jw H e 的对数幅频响应如下图 :下面产生一个信号来检验刚才所设计的滤波器组的实际性能,产生一个信号()x n ,包含两个正弦信号,频率分别为119,30f Hz f Hz == ,还包含一个最大幅值 0.2 的高斯白噪。
计算得()x n 的信噪比 SNR=19.6040dB 。
抽样频率 200Hz 下,用刚才所设计滤波器组进行处理,得到信号如下程序:clear all;close all;N0=512;%First step: To design a one-band filter G(z) by Chebyshev approximation% set the cutoff frequency of the G(w);F=[0 0.84 1 1];A=[1 1 0 0];N=23;B=firpm(N,F,A)a=1;wf=0:pi/N0:pi*(N0-1)/N0;wff=0:1/N0:(N0-1)/N0;Gw=freqz(B,a,wf);Ew=exp(i*N*wf/2);Gr=real(Gw.*Ew);gn=impz(B,a,N);%plot the response curvefigure(1);subplot(2,1,1)plot(wff,real(Gr));grid on;title('single-band filt G(jw)'); subplot(2,1,2)stem((1:N),gn,'filled')title('single-band filt g(n)') hold onplot((0:N),zeros(N+1),'b');grid on;% To obtain half-band filter P(z) from G(z),% F(z)=[G(z^2)+(N-1)/2]/2N1=47;s=length(B);B2=zeros(1,2*s-1);for k=1:s,B2(k*2-1)=B(k);end,N2=length(B2);B2(N+1)=1+B2(N+1); B2=B2/2;Pw=freqz(B2,a,wf);Ew=exp(i*N*wf);Pr=real(Pw.*Ew);pn=impz(B2,a,N1);figure(2);subplot(2,1,1)plot(wff,Pr);grid on;title('half-band filt H(jw)'); subplot(2,1,2)stem(pn,'filled');grid on;title('half-band filt h(n) ') ; hold onplot((0:N1),zeros(N1+1),'b');grid on;%Modify P(z) and prepare to do spectrum decompositionminP=min(Pr);B2(N+1)=B2(N+1)+abs(minP);B3=B2*0.5/(0.5+abs(minP));Pw0=freqz(B3,a,wf);Ew=exp(i*N*wf);Pr0=real(Pw0.*Ew);figure;plot(wff,Pr0);grid;title('Impulse Response of P(z)');%Spectrum AnalysisA0=zeros(1,N1);A0(1)=1;figure(3);subplot(121);zplane(B3,A0);title('the zeros and poles before resolve, P(z)')[Z,P,K]=tf2zp(B3,A0);Z1=sort(Z);ll=length(Z1)/2;ZZ=Z1(1:ll);temp=1;for m=1:ll ;temp=(-ZZ(m))*temp;end;if imag(temp)<0.0001temp=real(temp);elsedisp('Spectrum Decomposition Failed!');endKK=sqrt(K/temp);l2=length(ZZ);PP=zeros(l2,1);[H0Num,H0Den]=zp2tf(ZZ,PP,KK); subplot(122)zplane(H0Num,H0Den);title('the zeros and poles after resolve, H_0(z)')H1Num=qmf(H0Num,1);G0Num=-wrev(H0Num);G1Num=qmf(G0Num);%H0H0w=freqz(H0Num,H0Den,wf);h0n=impz(H0Num,H0Den);figure(4);subplot(2,1,1)plot(wff,abs(H0w));grid on;title('Amplitude-Frequency Response of H_0(z)');subplot(2,1,2)stem(h0n,'filled');grid on;title('Impulse Response ofH_0(z)') ;hold on;plot((0:N),zeros(N+1),'b');grid on;%H1H1w=freqz(H1Num,H0Den,wf);%Ew=exp(i*N*wf);%H1r=real(H1w.*Ew);h1n=impz(H1Num,H0Den);figure(5);subplot(2,1,1) plot(wff,abs(H1w));grid on;title('Amplitude-Frequency Response of H_1(z)');subplot(2,1,2)stem(h1n,'filled');grid on;title('Impulse Response ofH_1(z)')hold on;plot((0:N),zeros(N+1),'b');grid on;%G0G0w=freqz(G0Num,H0Den,wf);g0n=impz(G0Num,H0Den);figure(6);subplot(2,1,1)plot(wff,abs(G0w));grid on;title('Amplitude-Frequency Response of G_0(z)');subplot(2,1,2)stem(g0n,'filled');grid on;title('Impulse Response ofG_0(z)')hold on;plot((0:N),zeros(N+1),'b');grid on;%G1G1w=freqz(G1Num,H0Den,wf);g1n=impz(G1Num,H0Den);figure(7);subplot(2,1,1)plot(wff,abs(G1w));grid on;title('Amplitude-Frequency Response of G_1(z)');subplot(2,1,2)stem(g1n,'filled');grid on;title('Impulse Response ofG_1(z)')hold on;plot((0:N),zeros(N+1),'b');grid on;%features of filter group[H0,w]= freqz(h0n,a);[H1,w]= freqz(h1n,a);absH0=abs(H0);absH1=abs(H1);ah0=20*log10(absH0);ah1=20*log10(absH1);figure(8)plot(wff,ah0,'k-',wff,ah1,'b-'); grid on;xlabel('w/pi');ylabel('|H_0(e^j^ w)|/dB,|H_1(e^j^w)|/dB');sumh=absH0.*absH0+absH1.*absH1; sum=10*log10(sumh);save H_filters h0ndisp('Press any key to process a signal using the filters...'); pause;clear all;close all;load H_filtersh0=h0n;h1=qmf(h0,1);g0=-wrev(h0);g1=qmf(g0);fs=200;f1=8;f2=30;step=-15;N=1000;n=1:N;Sig1=2*sin(2*pi*f1*n/fs);Sig2=2*sin(2*pi*f2*n/fs);P1=var(Sig1+Sig2)Nos=0.2*randn(N,1);P2=var(Nos);snr=10*log10(P1/P2) Sig=Sig1'+Sig2'+Nos;%signal v0(n) and v1(n) after decompositon and decimationx0=filter(h0,1,Sig);v0=decimate(x0,2); %low passx1=filter(h1,1,Sig);v1=decimate(x1,2); % high pass%reconstructed signal by filter [g0(n) g1(n) ]u0=interp(v0,2);u1=interp(v1,2);x_recon=filter(g0,1,u0)+filter(g 1,1,u1);figure(9);subplot(311)plot(Sig(100:200));grid;ylabel('x(n)');subplot(312)plot(x_recon(100+step:200+step));grid;ylabel('x(n).approx'); subplot(313)plot(Sig(100:200),'k');grid;hold onplot(x_recon(100+step:200+step),'b');ylabel('x(n),x(n).approx');。