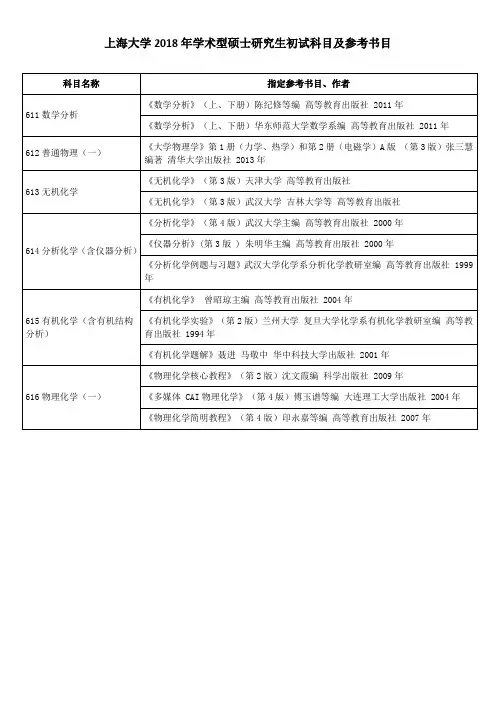
上海大学2018年硕士《量子力学》考试大纲

《量子力学》考试大纲
学院（盖章）：负责人（签字）：
专业代码：070201、070207、070205专业名称：理论物理、光学、凝聚态物理考试科目代码：803 考试科目名称：量子力学（一）考试内容
考试范围为理科院校物理系《量子力学》课程的基本内容。

以曾谨言著《量子力学导论》（第二版）（北京大学出版社）为篮板，内容涵盖该教材的第一至十章，波函数与薛定谔方程、一维定态问题、力学量用算符表达与表象变换、中心力场、定态问题的常用近似方法均在其中。

试题重点考查的内容：
一、波函数与薛定谔方程
1．波函数的统计诠释
2．态叠加原理
3．薛定谔方程
二、一维定态问题
1．方位势
2．一维散射问题
3．一维谐振子
三、力学量用算符表达与表象变换
1．算符的运算规则
2．厄米算符的本征值与本征函数
3．共同本征函数
4．量子力学的矩阵形式与表象变换
5．狄拉克符号
四、中心力场
1．中心力场中粒子运动的一般性质
2．球方势阱
3．氢原子
五、定态问题的常用近似方法
1．非简并态微扰论
2．简并态微扰论
（二）考试的基本要求
1．基本概念要清晰。

2．对知识要会综合运用。

3．具有必要的数学运算能力。

（三）考试基本题型
基本题型可能有：选择题、填空题、判断题、简答题、计算题和分析论述题等。

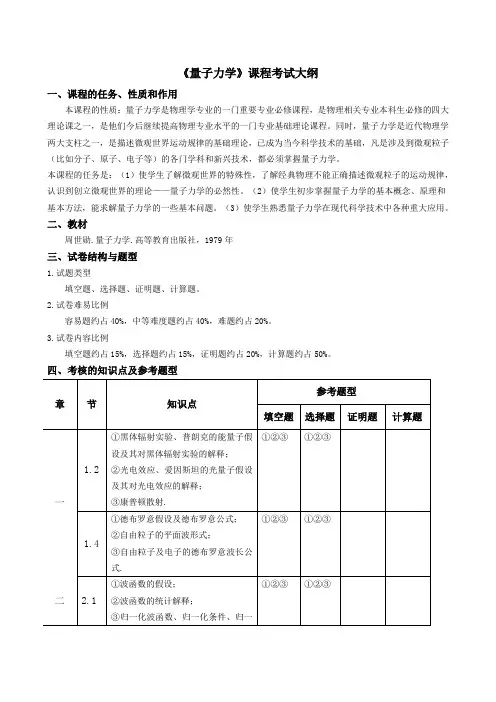
《量子力学》课程考试大纲
一、课程的任务、性质和作用
本课程的性质：量子力学是物理学专业的一门重要专业必修课程，是物理相关专业本科生必修的四大理论课之一，是他们今后继续提高物理专业水平的一门专业基础理论课程。

同时，量子力学是近代物理学两大支柱之一，是描述微观世界运动规律的基础理论，已成为当今科学技术的基础，凡是涉及到微观粒子（比如分子、原子、电子等）的各门学科和新兴技术，都必须掌握量子力学。

本课程的任务是：（1）使学生了解微观世界的特殊性，了解经典物理不能正确描述微观粒子的运动规律，认识到创立微观世界的理论——量子力学的必然性。

（2）使学生初步掌握量子力学的基本概念、原理和基本方法，能求解量子力学的一些基本问题。

（3）使学生熟悉量子力学在现代科学技术中各种重大应用。

二、教材
周世勋.量子力学.高等教育出版社，1979年
三、试卷结构与题型
1.试题类型
填空题、选择题、证明题、计算题。

2.试卷难易比例
容易题约占40%，中等难度题约占40%，难题约占20%。

3.试卷内容比例
填空题约占15%，选择题约占15%，证明题约占20%，计算题约占50%。

四、考核的知识点及参考题型。

2018年硕士研究生招生考试大纲019 基础教学中心目录初试考试大纲 1637专业基础综合 1659专业史论基础 2936 和声分析与曲式作品分析错误!未指定书签。

333教育综合错误!未指定书签。

937 教学设计错误!未指定书签。

942 教育管理学错误!未指定书签。

945 综合英语21复试考试大纲23复试专业综合23音乐文学创作24音乐文学理论24现场演奏科目：音乐文学与音乐表演（弦乐科目）25现场演奏科目：音乐文学与音乐表演（钢琴科目）错误!未指定书签。

现场演奏科目：音乐文学与音乐表演（声乐科目）错误!未指定书签。

现场演奏科目：音乐文学与音乐表演（萨克斯科目）错误!未指定书签。

教育技术学综合28管理学原理29课程与教学论错误!未指定书签。

音乐文学创作错误!未指定书签。

音乐文学理论错误!未指定书签。

现场演奏科目：弦乐科目36现场演奏科目：钢琴科目37现场演奏科目：声乐科目38现场演奏科目：萨克斯科目错误!未指定书签。

同等学力加试科目考试大纲错误!未指定书签。

教育学错误!未指定书签。

教育研究方法44初试考试大纲637专业基础综合一、考试性质体育综合包括运动生理学和运动训练学两部分内容。

是体育教育训练学专业硕士研究生入学考试的专业基础课程。

二、考察目标要求考生能系统理解运动生理学和运动训练学的基本概念和基本原理，能过运用基本理论合理地解释体育教学和运动训练中现象和问题。

三、考试形式本考试为闭卷考试，满分为300分，考试时间为180分钟。

四、考试内容（一）运动生理学（50%）考试内容：骨骼肌机能、血液、循环机能、呼吸机能、物质与能量代谢、肾脏机能、内分泌机能、感觉与神经机能、运动技能、身体素质、运动过程中人体机能状态变化的规律、运动训练原则的生理学分析、运动机能的生理学评定、儿少生长发育与体育运动。

（二）运动训练学（50%）考试内容：竞技体育与运动训练、运动成绩与竞技能力、运动训练原则、运动训练方法与手段、运动员体能及其训练、运动员技术能力及其训练、运动员的战术能力及其训练、运动员心理能力与运动智能及其训练、运动训练计划、运动队伍管理。

量子力学考试大纲适用于物理学所有学科Ⅰ考查目标理论物理、凝聚态物理、粒子物理与原子核物理、能源与材料物理、能源与材料工程、材料工程等专业研究生入学考试《量子力学》课程，重点考查考生掌握量子力学基本概念、基本原理以及运用量子力学基本理论解决具体相关物理问题的能力，为进一步学习其它专业课程或从事科研和教学工作奠定坚实的基础。

Ⅱ考试形式和试卷结构一、试卷满分及考试时间本试卷满分为150分，考试时间为180分钟。

二、答题方式答题方式为闭卷、笔试。

三、试卷内容结构波粒二象性、波函数和薛定谔方程 50分量子力学的力学量及其表象 50分微扰理论、自旋与全同粒子、粒子在电磁场中的运动 50分四、试卷题型结构简答题2小题，每小题10分，共20分证明题 2小题，每小题15分，共30分计算题4小题，每小题25分，共100分Ⅲ考查范围一、波粒二象性、波函数和薛定谔方程考查主要内容：（1）光的波粒二象性的实验事实及其解释。

（2）原子结构的玻尔理论和索末菲的量子化条件。

（3）德布罗意关于微观粒子的波粒二象性的假设。

（4）德布罗意波的实验验证。

（5）波函数的统计假设和量子态的表示形式。

（6）态叠加原理的内容及其物理意义。

（7）薛定谔方程和定态薛定谔方程的一般形式。

（8）粒子流密度的概念及粒子数守恒的物理内容。

（9）一维薛定谔方程求解的基本步骤和方法。

（10）几个典型的一维定态问题：a.一维无限深势阱；b.一维谐振子；c.一维方势垒；d.一维有限方势阱;e. 势。

二、量子力学的力学量及其表象考查主要内容：（1）动量算符的表示形式及其与坐标算符间的对易关系，动量算符本征函数的归一化。

（2）角动量算符的表示形式及其有关的对易关系，角动量算符2ˆL和z Lˆ的共同本征函数及所对应的本征值。

（3）电子在固定的正点电荷库仑场中运动的定态薛定谔方程及其求解的基本步骤；定态波函数的表示形式；束缚态的能级及其简并度；并由此讨论氢原子的能级、光谱线的规律、电子在核外的概率分布和电离能等。

)(Et r p i p Ae-⋅=ρϖηϖψ《量子力学》复习 提纲一、基本假设 1、（1）微观粒子状态的描述 （2）波函数具有什么样的特性 （3）波函数的统计解释2、态叠加原理（说明了经典和量子的区别）3、波函数随时间变化所满足的方程 薛定谔方程4、量子力学中力学量与算符之间的关系5、自旋的基本假设 二、三个实验1、康普顿散射（证明了光子具有粒子性） 第一章2、戴维逊-革末实验（证明了电子具有波动性） 第三章3、史特恩-盖拉赫实验（证明了电子自旋） 第七章 三、证明1、粒子处于定态时几率、几率流密度为什么不随时间变化；2、厄密算符的本征值为实数；3、力学量算符的本征函数在非简并情况下正交；4、力学量算符的本征函数组成完全系；5、量子力学测不准关系的证明；6、常见力学量算符之间对易的证明；7、泡利算符的形成。

四、表象算符在其自身的表象中的矩阵是对角矩阵。

五、计算1、力学量、平均值、几率；2、会解简单的薛定谔方程。

第一章 绪论1、德布洛意假设： 德布洛意关系：戴维孙-革末电子衍射实验的结果： 2、德布洛意平面波：3、光的波动性和粒子性的实验证据：4、光电效应：5、康普顿散射： 附：（1）康普顿散射证明了光具有粒子性（2）戴维逊-革末实验证明了电子具有波动性∑=nnn c ψψ1d 2=⎰τψ（全）()ψψψψμ∇-∇2=**ηϖi j ⎩⎨⎧≥≤∞<<=ax x a x x V 或0,0,0)(0=⋅∇+∂∂j tϖρ⎥⎦⎤⎢⎣⎡+∇-=),(222t r V H ϖημ)(,)(),(r er t r n tE i n n n ϖϖϖηψψψ-=n n n E H ψψ=（3）史特恩-盖拉赫实验证明了电子自旋第二章 波函数和薛定谔方程1．量子力学中用波函数描写微观体系的状态。

2．波函数统计解释：若粒子的状态用()t r ,ρψ描写，τψτψψd d 2*=表示在t 时刻，空间r ρ处体积元τd 内找到粒子的几率（设ψ是归一化的）。

《量子力学导论》考试大纲
一、考试目的
本考试是全日制光学、光子学与光子技术和凝聚态物理硕士学位研究生的入学资格考试之专业基础课，各语种考生统一用汉语答题。

根据考生参加本考试的成绩和其他三门考试的成绩总分来选择参加第二轮，即复试的考生。

二、考试的性质与范围
本考试是测试考生量子力学基础理论与方法的尺度参照性水平考试。

考试范围包括本大纲规定的量子力学基础理论与方法及其在实际问题中的运用。

三、考试基本要求
1、具备量子力学基本概念、理论和方法的相关知识。

2、具备运用量子力学基本概念、理论和方法解决实际问题的能力。

四、考试形式
本考试为闭卷考试，强调考生对于量子力学基本概念、基础理论和方法的理解和运用。

五、考试内容
本考试内容主要包括量子力学基本概念、基本理论和方法，以及运用量子力学基本概念、理论和方法解决具体问题。

考试时间为3小时，总分150分。

答题和计分
要求考生用钢笔或圆珠笔做在答题卷上。

1 / 1。

2018年硕士研究生招生考试大纲002 信息科学与工程学院目录初试考试大纲 1610高等数学 1638 量子力学 1953 声学基础 3806 普通物理 5807数据结构7808地理信息系统8810数字电子技术10341农业知识综合三11910高级程序设计12911软件工程14912数据结构和软件工程16930程序设计基础19940 计算机网络与安全 21946 信号与系统23954计算机基础综合24复试考试大纲28现代物理基础28科技英语(光学、凝聚态物理) 30现代光学基础31电子技术基础33科技英语（光学工程专业（学术型080300和专业型085202）34 电子技术A 35通信原理36计算机系统结构38面向对象的程序设计40数据库系统41程序设计实践43保密概论45安全程序设计实践47农业信息化概论50数字信号处理52C++语言编程54科技英语（地图学与地理信息系统、测绘工程）56 光学电磁学57信号与系统59数字电子技术61科技英语（海洋探测技术、摄影测量与遥感）62同等学力加试科目考试大纲63数据结构63软件工程65初试考试大纲610高等数学一、考试性质高等数学是理、工科专业硕士研究生入学考试的专业基础课程。

高等数学入学考试是为招收理、工科专业硕士研究生而实施的具有选拔功能的水平考试，它的指导思想是既要为国家选拔具有较强分析问题与解决问题能力的高层次人才，又要有利于促进高等学校高等数学课程教学质量的提高。

二、考察目标要求考生能系统理解高等数学的基本概念和基本原理，掌握高等数学的基本思想与方法，具有较好的逻辑推理能力、空间想象能力、计算能力以及运用所学知识分析问题和解决问题的能力。

三、考试形式本考试为闭卷考试，满分为150分，考试时间为180分钟。

试卷结构：高等数据75%，线性代数25%。

四、考试内容（一）高等数学（75%）考试内容：函数的极限与连续，一元函数微积分及其应用，向量代数与空间解析几何，多元函数微积分及其应用，场论，含参变量积分，无穷级数，常微分方程及其应用。

为了帮助广大考生复习备考，也应广大考生的要求，现提供我校自命题专业课的考试大纲供考生下载。

考生在复习备考时，应全面复习，我校自命题专业课的考试大纲仅供参考。

上海电力学院
2018年硕士研究生入学复试《量子力学》课程考试大纲
一、参考书目：
《量子力学教程》. 高教出版社（第二版）. 周世勋原著陈灏修订二、复习的总体要求
要求考生熟悉量子理论的物理图象，掌握基本概念和基本理论，能熟练运用相应的数学方法求解基本的量子体系。

三、主要复习内容
1.绪论
熟悉光波-粒二象性的主要是实验基础；
掌握德布罗意微观粒子的波粒二象性的假设（德布罗意关系）
2.波函数和薛定谔方程
理解波函数的统计解释；掌握态叠加原理；理解薛定谔方程的建立过程；会求解某些特定一维定态问题（一维无限深方势阱和一维线性谐振子）。

3.量子力学中的力学量
掌握算符的基本运算规则，理解量子力学中表示力学量的厄米算符的基本性质；掌握动量和角动量等相关算符的本征值、本征函数（正交归一性）及其对易关系；掌握力学量平均值的计算方法（力学量的可能值、概率和平均值），理解力学量有确定值的条件；理解测不准关系
4. 态和力学量的表象。