模态频率响应分析
- 格式:docx
- 大小:656.26 KB
- 文档页数:4

有限元分析类型一、nastran中的分析种类(1)静力分析静力分析是工程结构设计人员使用最为频繁的分析手段,主要用来求解结构在与时间无关或时间作用效果可忽略的静力载荷(如集中载荷、分布载荷、温度载荷、强制位移、惯性载荷等)作用下的响应、得出所需的节点位移、节点力、约束反力、单元内力、单元应力、应变能等。
该分析同时还提供结构的重量和重心数据。
(2)屈曲分析屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,NX Nastran中的屈曲分析包括两类:线性屈曲分析和非线性屈曲分析。
(3)动力学分析NX Nastran在结构动力学分析中有非常多的技术特点,具有其他有限元分析软件所无法比拟的强大分析功能。
结构动力分析不同于静力分析,常用来确定时变载荷对整个结构或部件的影响,同时还要考虑阻尼及惯性效应的作用。
NX Nastran的主要动力学分析功能:如特征模态分析、直接复特征值分析、直接瞬态响应分析、模态瞬态响应分析、响应谱分析、模态复特征值分析、直接频率响应分析、模态频率响应分析、非线性瞬态分析、模态综合、动力灵敏度分析等可简述如下:❑正则模态分析正则模态分析用于求解结构的固有频率和相应的振动模态,计算广义质量,正则化模态节点位移,约束力和正则化的单元力及应力,并可同时考虑刚体模态。
❑复特征值分析复特征值分析主要用于求解具有阻尼效应的结构特征值和振型,分析过程与实特征值分析类似。
此外Nastran的复特征值计算还可考虑阻尼、质量及刚度矩阵的非对称性。
❑瞬态响应分析(时间-历程分析)瞬态响应分析在时域内计算结构在随时间变化的载荷作用下的动力响应,分为直接瞬态响应分析和模态瞬态响应分析。
两种方法均可考虑刚体位移作用。
直接瞬态响应分析该分析给出一个结构随时间变化的载荷的响应。
结构可以同时具有粘性阻尼和结构阻尼。
该分析在节点自由度上直接形成耦合的微分方程并对这些方程进行数值积分,直接瞬态响应分析求出随时间变化的位移、速度、加速度和约束力以及单元应力。
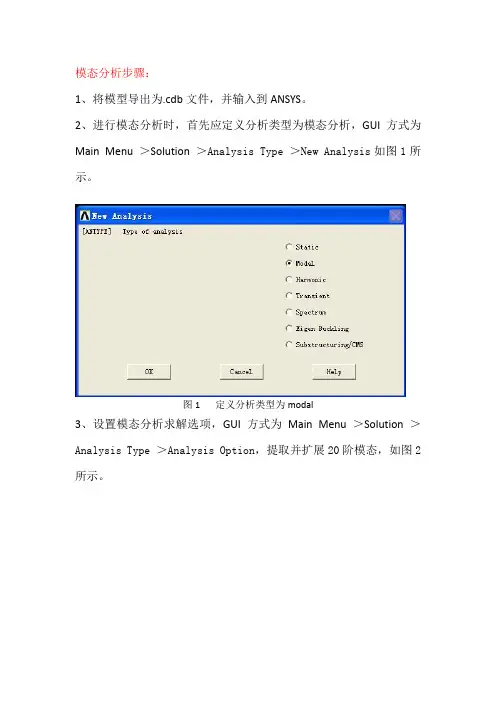
模态分析步骤:1、将模型导出为.cdb文件,并输入到ANSYS。
2、进行模态分析时,首先应定义分析类型为模态分析,GUI方式为Main Menu >Solution >Analysis Type >New Analysis如图1所示。
图1 定义分析类型为modal3、设置模态分析求解选项,GUI方式为Main Menu >Solution >Analysis Type >Analysis Option,提取并扩展20阶模态,如图2所示。
图2 Modal Analysis对话框4、设置B lock lanczos(分块蓝索斯)方法求解选项。
单击图2中的OK按钮,弹出Block Lanczos Method 对话框,将起始频率改为1,单击OK按钮,如图3所示。
图3 Block Lanczos Method对话框5、求解并查看结果。
采用GUI方式提交求解:Main Menu >Solution>Solve>Current LS。
(注意:下面的模态图下面标明是第。
阶模态振型)谐响应分析的基本步骤:1.将模型导出为.cdb文件,并输入到ANSYS中。
2.模态分析由于峰值响应发生在激励的频率和结构的固有频率相等之时,所以在进行谐响应分析之前,应首先进行模态分析,以确定结构的固有频率,计算前20阶模态频率。
3.完成模态分析后,退出后处理器,GUI方式为Main Menu>Finish。
4.定义分析类型为谐响应分析,GUI方式为Main Menu>Solution>Analysis Type>New Analysis,如图4所示。
图4 定义分析类型为Harmonic5、设置谐响应分析求解选项,GUI方式为Main Menu>Solution>Analysis Type>Analysis Options,保持默认选项,采用完全法,如图5所示。
图5 Harmonic Analysis对话框6、单击图5中的OK按钮,弹出Full Harmonic Analysis对话框,保持默认设置,单击OK按钮,如图6所示。

通常结构的频率响应是一次求解就可以计算出来。
对于模态法的频率响应问题,还可以分成两步来求解,即第一步先结算结构的固有频率,第二步在已计算的固有频率基础上再进行频率响应的计算。
对于某些场合这样的计算方法是有用处的。
比如结构受多个载荷分别激励,需要计算不同载荷下结构的频率响应。
这种情况下就可以使用上述方法来提高计算效率(省去了模态计算的时间)。
下面介绍如何使用Patran 和Nastran 来实现模态 – 频率响应的分步分析。
1. 按正常模态分析的步骤建立结构模态分析的模型,定义材料和单元属性以及边界条件等。
2. 进行求解设置,在设定solution type 时选择Normal Modes ,并选中Interactive Modal Analysis 选项,如下图。
3. 其它的设置和正常的模态分析一样。
在Subcase Select 中选择所有要分析的工况,Apply 后生成bdf 文件,并求解,或直接在Patran 中递交求解。
手动启动Nastran 进行求解时注意不能设置参数 SCR=YES ,包括在Nastran 的配置文件中。
4.模态求解完成后,接下来就可以使用模态的求解结果进行频率响应的分析。
选择Analysis 菜单,设置Object为:interactive5. 选者DBALL文件,如下图:6.接下来创建载荷,点击Create Loading,如下图。
对载荷进行逐项设置。
7.再定义结果输出。
点击Output Request,在其中定义激励频率和节点以及单元的输出。
8.定义完成后按Apply求解(Full Run形式),或者生成bdf文件,手动递交分析。
9.计算完成后,点击View Result菜单,可读入结果,进行后处理,如下图。
在此菜单下的后处理只能画出各种曲线。
10.如需观看云图,可使用读入xdb文件的方法。
菜单:Analysis -> Access results -> Attach XDB。

有限元分析类型一、nastran中的分析种类(1)静力分析静力分析是工程结构设计人员使用最为频繁的分析手段,主要用来求解结构在与时间无关或时间作用效果可忽略的静力载荷(如集中载荷、分布载荷、温度载荷、强制位移、惯性载荷等)作用下的响应、得出所需的节点位移、节点力、约束反力、单元内力、单元应力、应变能等。
该分析同时还提供结构的重量和重心数据。
(2)屈曲分析屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,NX Nastran中的屈曲分析包括两类:线性屈曲分析和非线性屈曲分析。
(3)动力学分析NX Nastran在结构动力学分析中有非常多的技术特点,具有其他有限元分析软件所无法比拟的强大分析功能。
结构动力分析不同于静力分析,常用来确定时变载荷对整个结构或部件的影响,同时还要考虑阻尼及惯性效应的作用。
NX Nastran的主要动力学分析功能:如特征模态分析、直接复特征值分析、直接瞬态响应分析、模态瞬态响应分析、响应谱分析、模态复特征值分析、直接频率响应分析、模态频率响应分析、非线性瞬态分析、模态综合、动力灵敏度分析等可简述如下:❑正则模态分析正则模态分析用于求解结构的固有频率和相应的振动模态,计算广义质量,正则化模态节点位移,约束力和正则化的单元力及应力,并可同时考虑刚体模态。
❑复特征值分析复特征值分析主要用于求解具有阻尼效应的结构特征值和振型,分析过程与实特征值分析类似。
此外Nastran的复特征值计算还可考虑阻尼、质量及刚度矩阵的非对称性。
❑瞬态响应分析(时间-历程分析)瞬态响应分析在时域内计算结构在随时间变化的载荷作用下的动力响应,分为直接瞬态响应分析和模态瞬态响应分析。
两种方法均可考虑刚体位移作用。
直接瞬态响应分析该分析给出一个结构随时间变化的载荷的响应。
结构可以同时具有粘性阻尼和结构阻尼。
该分析在节点自由度上直接形成耦合的微分方程并对这些方程进行数值积分,直接瞬态响应分析求出随时间变化的位移、速度、加速度和约束力以及单元应力。

第八章频率响应分析8.1 概述1)计算震荡激励的响应2) 激励在频域中显式定义,在每频率点作用力已知3) 计算的响应通常包括节点位移、单元力和应力4) 计算的响应为复数、由大小、相位定义5) 频率响应分析分为直接法、模态法。
8.2 直接频率响应法1)动力学方程2)在MATi卡中PARAM,G和GE 不形成阻尼矩阵、而形成复刚度矩阵其中,与瞬态响应对应有8.3 模态频率响应法1)转化为模态坐标中,求解解耦的单自由度系统得2)求解该方程比直接法更快3)如无阻尼或仅有模态阻尼(TABDMP1定义),方程才能解耦;否则,如果出现非模态阻尼(VISC,DAMP定义),使用低效率得直接频响法(对小的模态坐标矩阵)。
8.4 激励的确定1)定义为频率的函数2)MSC/NASTRAN中的几种定义• RLOAD1: 用实部和虚部定义频变载荷• RLOAD2 :用大小和相位定义频变载荷• LSEQ :用静态载荷产生动态载荷3)用 DLOAD数据集卡组合频变力4)RLOADi卡由DLOAD 情况控制卡选择8.4.1 RLOAD1卡片1) 定义如下频变载荷2) 格式3) 由DLOAD=SID.选取8.4.2 RLOAD2卡片1) 定义如下频变载荷2)格式3) 由DLOAD=SID.选取8.4.3 FREQ卡片1) 选择频率步长大小2) FREQ卡片定义离散激励频率3) FREQ1 定义f START, 频率增量、增量数目4)FREQ2定义f START, f end对数间隔数5)FREQ3 定义F1, F2和在二者间线性或对数插值数目(基于朝两端点或中心)6)FREQ4 指定一个共振频率、一个等效的间隔频率数(在激励频率内)7)FREQ5 指定一个频率范围和频率范围内的固有频率的分数8)FREQ3, FREQ4, FREQ5 仅对模态法有效9)FREQi 数据卡由FREQUENCY =SID情况控制卡选取10)所有FREQi数据卡用相同的ID11)FREQ, FREQ1, FREQ2, FREQ3, FREQ4和FREQ5 卡可以在同一分析中使用8.4.3.1 FREQ卡1) 定义频率响应分析中的频率集2) 格式3) 由情况控制卡FREQUENCY = SID.选取1) 定义频率响应问题中频率集:通过开始频率、频率增量、增量数目2) 格式3) 由情况控制卡FREQUENCY = SID选取4) f i= F1 + DF * (i - 1)5) 单位:cycles per unit time.8.4.3.3 FREQ21) 定义频率响应问题中频率集,通过开始频率、结束频率、对数增量数目2) 格式3) 由情况控制卡FREQUENCY = SID选取4) 单位:cycles per unit time5)1) 定义频率响应问题中频率集,通过指定两模态频率间的激励频率数2) 格式3) 仅用于模态频率响应4) 由情况控制卡FREQUENCY = SID选取5) 对各种CLUSTER其中,6)) 例子(F1=10,F2=20,NEF=11,TYPE=LINEAR)8.3.3.5 FREQ4卡1) 定义频率响应问题中频率集,通过指定范围内每阶固有频率附近激励频率数2) 格式3) 仅用于模态频率响应4) 由情况控制卡FREQUENCY = SID选取8.3.3.6 FREQ5卡1) 定义频率响应问题中频率集,通过指定频率范围及该范围内的位置2) 格式3) 如f N1为F1和F2间的固有频率,则4) 仅用于模态频率响应5) 由情况控制卡FREQUENCY = SID选8.5 模态频率响应与直接频率响应比较注:“X”表可用8.6 SORT1和SORT2输出1) SORT1输出每一激励频率点2) SORT2输出给定节点、单元的结果8.7 频率响应求解控制8.7.1 执行控制8.7.2 情况控制8.7.3 数据模型集8.7.4 输出控制1)结点结果输出2)单元输出结果3)其它8.8 频变弹簧和阻尼器(1) 弹簧刚度和阻尼器阻尼系数为频变函数(2) CBUSH定义一般弹簧、阻尼连接(3) PBUSH定义名义上的弹簧、阻尼连接(4) PBUSHT定义变频弹簧、阻尼器的值8.8.1 CBUSH 卡片1)定义广义弹簧-阻尼器结构单元,可为非线性或频变2)格式8.8.2 PBUSH卡片1)定义广义弹簧-阻尼器结构单元性质2)格式8.8.3 PBUSHT卡片1)定义广义弹簧-阻尼器的频变或力变性质2)格式8.8.4 例子SAMPLE USING CBUSH ELEMENT$$ cbush1.dat$TIME 10SOL 108CENDTITLE = VERIFICATION PROBLEM, FREQ. DEP. IMPEDANCE BUSHVER SUBTITLE = SINGLE DOF, CRITICAL DAMPING, 3 EXCITATION FREQUENCIES ECHO = BOTHSPC = 1002DLOAD = 1DISP = ALLFREQ = 10ELFO = ALLBEGIN BULK$ CONVENTIONAL INPUT FOR MOUNTGRDSET,, , , , , ,23456 $ PS$ TIE DOWN EVERYTHING BUT THE 1 DOFGRID, 11, , 0., 0., 0.0 $ GROUND=, 12, =, =, =, , $ ISOLATED DOFSPC1, 1002 123456 11 $ GROUNDCONM2, 12, 12, , 1.0 $ THE ISOLATED MASS$$ EID PID GA GB GO/X1 X2 X3 CID$CBUSH 1000 2000 11 12 0$PBUSH 2000 K 1.0B 0.0$PBUSHT 2000 K 2001B 2002$TABLED1, 2001 $ STIFFNESS TABLE, 0.9 0.81, 1.0, 1.0, 1.1, 1.21 ENDTTABLED1 2002 $ DAMPING TABLE, 0.9 .2864789, 1.0,.318309, 1.1,.3501409 ENDT$CONVENTIONAL INPUT FOR FREQUENCY RESPONSEPARAM, WTMASS, .0253303 $ 1/(2*PI)**2. GIVES FN=1.0DAREA, 1, 12, 1, 2. $CAUSES UNIT DEFLECTIONFREQ, 10, 0.9, 1.0, 1.1 $ BRACKET THE NATURAL FREQUENCYRLOAD1, 1, 1, , , 3TABLED1,3 $ TABLE FOR FORCE VS. FREQUENCY, 0.9, 0.81, 1., 1., 1.1, 1.21,ENDT $ P = KENDDATA例2,直接频响法激励为作用在角点的单位载荷,频率范围在20~1000间,频率步为20HZ, 结构阻尼g=0.06.INPUT FILE FOR PROBLEM #5ID SEMINAR, PROB5SOL108TIME30CENDTITLE = FREQUENCY RESPONSE DUE TO UNIT FORCE AT TIPECHO = UNSORTEDSPC = 1SET 111 = 11, 33, 55DISPLACEMENT(SORT2, PHASE) = 111SUBCASE 1DLOAD = 500FREQUENCY = 100$OUTPUT (XYPLOT)$XTGRID= YESYTGRID= YESXBGRID= YESYBGRID= YESYTLOG= YESYBLOG= NOXTITLE= FREQUENCY (HZ)YTTITLE= DISPLACEMENT RESPONSE AT LOADED CORNER, MAGNITUDE YBTITLE= DISPLACEMENT RESPONSE AT LOADED CORNER, PHASE XYPLOT DISP RESPONSE / 11 (T3RM, T3IP)YTTITLE= DISPLACEMENT RESPONSE AT TIP CENTER, MAGNITUDEYBTITLE= DISPLACEMENT RESPONSE AT TIP CENTER, PHASEXYPLOT DISP RESPONSE / 33 (T3RM, T3IP)YTTITLE= DISPLACEMENT RESPONSE AT OPPOSITE CORNER, MAGNITUDE YBTITLE= DISPLACEMENT RESPONSE AT OPPOSITE CORNER, PHASEXYPLOT DISP RESPONSE / 55 (T3RM, T3IP)$BEGIN BULKparam,post,0PARAM, COUPMASS, 1PARAM, WTMASS, 0.00259$$ PLATE MODEL DESCRIBED IN NORMAL MODES EXAMPLE$INCLUDE ’plate.bdf’$$ SPECIFY STRUCTURAL DAMPING$PARAM, G, 0.06$$ APPLY UNIT FORCE AT TIP POINT$RLOAD2, 500, 600, , ,310$DAREA, 600, 11, 3, 1.0$TABLED1, 310,, 0., 1., 1000., 1., ENDT$$ SPECIFY FREQUENCY STEPS$FREQ1, 100, 20., 20., 49$ENDDATA例3,模态频响法激励为振幅为0.1 psi的分布载荷与作用在角点的1.0 lb集中力,相位为45度。

定性地说,就是因为力的步调与振动步调相同,物体向右力向右,物体向左力向左,力始终做正功,所以振动能量不断增加。
其实不是说一般取前5阶。
根据不同的对象和边界条件,取得阶数都不同。
对于没有约束的对象,前6阶为刚体移动模态,频率为0;而对于有约束的对象,则没有刚体模态。
各阶振型的话就是各阶的振动形态,有横向振动,扭转振动,拉伸振动,这些需要你观察振型来判断。
你想理解模态必须去看一些振动学的书籍。
简单的讲物体的实际振动是各阶模态的叠加效果。
物体理论上有无穷阶模态,振动是这无穷阶模态的叠加。
但是实际上各阶模态对系统振动的贡献度不同,一般前几阶比较大,越往后越小,所以一般截取前面的模态。
如果说前5阶自振频率如果任何一阶数值处于外界激励的频率范围之内,就表明此物体在当前约束条件和激励下会发生共振吗?然后那一阶的振型就表示当时的振动形态还是什么?为什么个别振型弯扭组合都有而且形态这么夸张呢?谢谢!回答按照你说的的确有可能发生共振。
我说了实际振动是各阶模态叠加的效果,每一阶模态只是把原本耦合的各阶模态解耦出来呈现。
而不是你说的当时的振动形态。
所以你所看到的很夸张的形态也印证了我的话,因为那并不是实际振动情况。
请你结合我前一段回答体会。
按照我的理解,每个物体都有自己的共振频率,而且还有不止一个共振频率。
可能十几Hz 的时候会发生共振,几百Hz的时候又会发生共振。
如果进行模态分析,就是说把这个物体的共振频率都找出来。
如果把这些共振频率都按照频率值从小到大排,就是“阶”。
比如说最小的共振频率就是一阶。
模态分析是指采用振型分解法计算结构的各阶振型,包括各阶模态的频率、振型等。
指的是振型分解法中的一阶、二阶振型。
机械振动是由多个振动源叠加后的共同作用效果。
比如一个弹性体,在一定的约束下,会以某(些)个方式振动。
譬如一个弹簧,可能伸缩振动,也可能弯曲振动。
每一个振动方式,都有一个对应的振动频率,即固有频率。
模态分析,就是用有限元的方法,在某个范围内(譬如3000Hz以下),找出这些振动方式及其对应的频率。



nastran频率响应分析详细步骤(模态法)1.边界条件1.1约束1.2载荷1.2.1静载荷力forces 强迫位移darea压强pload力矩moment1.2.2频率—载荷函数▲TABLED1TABLED1:通过坐标点创建频率—载荷函数TABLED1_mum=坐标点数量x(i):频率坐标数值y(i):载荷倍数坐标值▲TABLED2TABLED2通过坐标点创建频率—载荷函数TABLED2mum=坐标点数量X1:x坐标延迟量x(i):频率坐标数值y(i):载荷倍数坐标值y=yt(x-X1)▲TABLED3TABLED3通过坐标点创建频率—载荷函数TABLED3mum=坐标点数量X1:x坐标延迟量X2:x坐标缩减倍数x(i):频率坐标数值y(i):载荷倍数坐标值y=yt((x-X1)/X2)▲TABLED41.2.3动力载荷RLOAD2:EXCITEID:选择已建好的静载荷TB:选择已建好的频率—载荷函数TYPE:载荷类型1.2.4动载频率选择—FREQi▲FREQ—频率列表选择离散的频率值NUMBER_OF_FREQ:频率数量F(i):频率数值▲FREQ1—频率加法增量通过开始频率、频率增量、增量数量来对频率进行抽样。
F1:开始频率DF:频率增量NDF:增量数量NUMBER_OF_FREQ1=抽样组数量▲FREQ2—频率乘法增量在抽样区间内抽取一组相邻比例相等的频率F1:抽样区间下限频率(必须大于0)F2:抽样区间上限频率NF:把抽样区间分为NF+1个点取样;每个点的关系为F(n):F(n-1)=F(n-1):F(n-2); n表示第n个抽样频率。
NUMBER_OF_FREQ2:抽样组数量▲FREQ3—固有频率区间抽样在模态固有频率点之间平均/对数抽样只适用于模态法频率响应分析。
F1:起始频率F2:结束频率NEF:相邻模态固有频率区间的抽样数量NUMBER_OF_FREQ3:抽样组数量▲FREQ4—固有频率扩展在抽样区间中的每个模态固有频率点进行一定宽度及密度的扩展抽样只适用于模态频率响应分析F1:抽样区间下限频率F2:抽样区间上限频率FSPD:抽样频率点扩展宽度系数。

结构振动的频率响应与模态分析频率响应与模态分析是结构振动研究中非常重要的方法,通过这些分析可以深入了解结构的特性、性能和振动行为。
本文将探讨频率响应与模态分析的基本原理、应用以及分析方法。
一、频率响应分析频率响应分析是研究结构在不同激励频率下的振动响应情况。
它通过测量系统对于不同频率激励下的振动响应,得到结构的频率响应函数,进而了解其固有频率、阻尼特性等。
其基本原理是利用傅里叶变换将时域信号转换为频域信号,得到频率和振幅之间的关系。
频率响应分析主要包括两个方面:幅频特性和相频特性。
幅频特性描述了结构对于不同频率激励振幅的响应情况,相频特性则反映了结构振动的相位角与激励频率之间的关系。
在实际工程中,频率响应分析可应用于结构的动态特性测试、模态参数辨识、振动响应控制等方面。
通过频率响应分析,可以预测结构的固有频率,找出结构的共振点,分析结构的阻尼、模态分布等重要参数,为结构设计和改进提供关键依据。
二、模态分析模态分析是研究结构的固有振动模态以及相应的振动特性。
通过模态分析可以获得结构的模态参数,包括自振频率、振型和阻尼比等。
在模态分析中,首先要建立结构的数学模型,通常采用有限元法等数值计算方法。
然后通过计算结构的特征值和特征向量,得到结构的固有频率和振型。
固有频率是结构振动的固有特性,而振型描述了结构在不同固有频率下的振动形态。
模态分析广泛应用于结构设计、振动控制、结构健康监测等领域。
通过模态分析,可以确定结构的主要振型和固有频率范围,评估结构的动态性能,优化结构的设计参数。
三、频率响应与模态分析的联系与应用频率响应分析与模态分析虽然从不同角度研究结构的振动特性,但它们之间存在紧密的联系和相互依赖。
首先,通过频率响应分析可以识别结构的固有频率。
在频率响应测试中,当激励频率接近结构的固有频率时,会发生共振现象,振动响应大幅增加。
通过识别这些共振点,可以初步估计结构的固有频率,并为后续的模态分析提供初步数据。

有限元分析类型一、nastran中的分析种类(1)静力分析静力分析是工程结构设计人员使用最为频繁的分析手段,主要用来求解结构在与时间无关或时间作用效果可忽略的静力载荷(如集中载荷、分布载荷、温度载荷、强制位移、惯性载荷等)作用下的响应、得出所需的节点位移、节点力、约束反力、单元内力、单元应力、应变能等。
该分析同时还提供结构的重量和重心数据。
(2)屈曲分析屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,NX Nastran中的屈曲分析包括两类:线性屈曲分析和非线性屈曲分析。
(3)动力学分析NX Nastran在结构动力学分析中有非常多的技术特点,具有其他有限元分析软件所无法比拟的强大分析功能。
结构动力分析不同于静力分析,常用来确定时变载荷对整个结构或部件的影响,同时还要考虑阻尼及惯性效应的作用。
NX Nastran的主要动力学分析功能:如特征模态分析、直接复特征值分析、直接瞬态响应分析、模态瞬态响应分析、响应谱分析、模态复特征值分析、直接频率响应分析、模态频率响应分析、非线性瞬态分析、模态综合、动力灵敏度分析等可简述如下:❑正则模态分析正则模态分析用于求解结构的固有频率和相应的振动模态,计算广义质量,正则化模态节点位移,约束力和正则化的单元力及应力,并可同时考虑刚体模态。
❑复特征值分析复特征值分析主要用于求解具有阻尼效应的结构特征值和振型,分析过程与实特征值分析类似。
此外Nastran的复特征值计算还可考虑阻尼、质量及刚度矩阵的非对称性。
❑瞬态响应分析(时间-历程分析)瞬态响应分析在时域内计算结构在随时间变化的载荷作用下的动力响应,分为直接瞬态响应分析和模态瞬态响应分析。
两种方法均可考虑刚体位移作用。
直接瞬态响应分析该分析给出一个结构随时间变化的载荷的响应。
结构可以同时具有粘性阻尼和结构阻尼。
该分析在节点自由度上直接形成耦合的微分方程并对这些方程进行数值积分,直接瞬态响应分析求出随时间变化的位移、速度、加速度和约束力以及单元应力。
模态分析的知道回答本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March定性地说,就是因为力的步调与振动步调相同,物体向右力向右,物体向左力向左,力始终做正功,所以振动能量不断增加。
其实不是说一般取前5阶。
根据不同的对象和边界条件,取得阶数都不同。
对于没有约束的对象,前6阶为刚体移动模态,频率为0;而对于有约束的对象,则没有刚体模态。
各阶振型的话就是各阶的振动形态,有横向振动,扭转振动,拉伸振动,这些需要你观察振型来判断。
你想理解模态必须去看一些振动学的书籍。
简单的讲物体的实际振动是各阶模态的叠加效果。
物体理论上有无穷阶模态,振动是这无穷阶模态的叠加。
但是实际上各阶模态对系统振动的贡献度不同,一般前几阶比较大,越往后越小,所以一般截取前面的模态。
如果说前5阶自振频率如果任何一阶数值处于外界激励的频率范围之内,就表明此物体在当前约束条件和激励下会发生共振吗然后那一阶的振型就表示当时的振动形态还是什么为什么个别振型弯扭组合都有而且形态这么夸张呢谢谢!回答按照你说的的确有可能发生共振。
我说了实际振动是各阶模态叠加的效果,每一阶模态只是把原本耦合的各阶模态解耦出来呈现。
而不是你说的当时的振动形态。
所以你所看到的很夸张的形态也印证了我的话,因为那并不是实际振动情况。
请你结合我前一段回答体会。
按照我的理解,每个物体都有自己的共振频率,而且还有不止一个共振频率。
可能十几Hz 的时候会发生共振,几百Hz的时候又会发生共振。
如果进行模态分析,就是说把这个物体的共振频率都找出来。
如果把这些共振频率都按照频率值从小到大排,就是“阶”。
比如说最小的共振频率就是一阶。
模态分析是指采用振型分解法计算结构的各阶振型,包括各阶模态的频率、振型等。
指的是振型分解法中的一阶、二阶振型。
机械振动是由多个振动源叠加后的共同作用效果。
比如一个弹性体,在一定的约束下,会以某(些)个方式振动。
结构模态及频率响应分析与优化设计结构模态及频率响应分析与优化设计是结构工程中的重要内容。
通过对结构的模态分析和频率响应分析,可以了解结构的振动特性和动态响应,并通过优化设计来改善结构的性能。
结构模态分析是指通过数值模拟和计算方法,计算结构在自由振动状态下的固有频率和振型。
固有频率是结构的固有特性,振型则是结构在特定频率下的振动形态。
通过模态分析,可以了解结构的固有频率分布情况,以及各个模态的振型特征。
模态分析的步骤主要包括:建立结构的有限元模型、求解结构的特征值问题、计算模态振型和固有频率。
有限元模型是通过离散化方法将结构划分为有限个单元,并根据单元的性质和连接关系构建刚度矩阵和质量矩阵。
求解特征值问题即求解结构的特征值和特征向量,通常采用迭代计算方法。
计算模态振型和固有频率则是根据特征值和特征向量计算得到的结果。
通过模态分析,可以得到结构的固有频率和振型信息,进而对结构的振动特性进行分析和评估。
例如,可以判断结构是否存在共振现象,即结构在某一频率下受到外力激励时,振动幅值会不断增大。
共振会引发结构的破坏和失稳,因此需要避免共振频率与外力频率相近的情况。
另外,模态分析还可以用于结构的设计优化,例如通过调整结构的几何形状、材料参数或支撑条件等,来改变结构的固有频率和振型,从而满足设计要求。
频率响应分析是指通过数值模拟和计算方法,计算结构在受到外力激励时的动态响应。
频率响应分析可以用于评估结构的动态性能和振动稳定性,以及分析结构在地震、风荷载等自然灾害下的响应情况。
频率响应分析的步骤主要包括:建立结构的有限元模型、施加外力激励、求解结构的动态响应。
有限元模型的建立和求解方法与模态分析类似,不同之处在于需要施加外力激励,即将结构在受力条件下进行分析。
外力激励可以是单点力、均布载荷、地震波等。
求解结构的动态响应则是通过数值计算方法,计算得到结构在不同频率下的振动幅值和相位。
通过频率响应分析,可以得到结构在不同频率下的振动响应情况,进而判断结构是否满足设计要求。
商用车驾驶室频率响应分析规范目录前言 (II)1 范围 (1)2 名词定义 (1)3 分析软件 (1)4 驾驶室频率响应分析作用 (1)5 数据输入 (2)6 建模要求 (3)7 约束条件 (3)8 载荷条件 (3)9 输出数据及文件格式 (3)10 分析频率设定 (3)11 分析工况 (3)12 注意事项 (3)13 商用车驾驶室频率响应分析步骤 (4)13.1 软件启动及分析模块选择 (4)13.2 打开驾驶室CAE模型 (4)13.3 建立单位载荷集 (4)13.4 建立载荷集表格 (5)13.5 建立动态载荷集 (6)13.6 建立频率载荷集 (6)13.7 建立模态载荷集 (7)13.8 建立频率响应分析工况 (7)13.9 设置控制卡片 (8)13.10 计算频率响应分析工况 (9)13.11 查看结果文件 (10)前言在汽车驾驶室的性能中,频率响应计算占有重要的地位,其作用主要表现在驾驶室疲劳寿命和整车乘坐的舒适性上。
汽车在行驶的过程中,会受到各种各样的动载荷。
当动载荷与车身的动力学特性接近,即动载荷的某分量与驾驶室的某阶模态的固有频率接近时,将可能引发结构共振产生较高的动应力,导致驾驶室的疲劳破坏。
而驾驶室的动力学特性对乘坐舒适性的影响,主要表现在NVH 性能上。
频率响应是指计算结构在周期振荡载荷作用下对每一个计算频率的动响应。
激励载荷是在频域中明确定义的,所有的外力在每一个指定的频率上已知。
力的形式可以是外力,也可以是强迫运动(位移、速度、加速度等)。
计算结果分实部和虚部两部分。
实部代表响应的幅度,虚部代表响应的相角。
通常频率响应采用响应的幅值来表示,包括节点位移、加速度、单元力和应力等。
频率响应的计算方法主要有直接频率响应、模态频率响应两种。
直接频率响应,通过求解整个模型的阻尼耦合方程,得出各频率对于外载荷的响应。
模态频率响应,利用结构的模态振型来对耦合的运动方程进行缩减和解耦,同时由单个模态响应的叠加得到某一给定频率下的解。
直接频率响应分析
分析原理
模态频率响应是在模态空间中,将模态进行线性叠加得到频率响应函数,模态频率响应的计算速度要比直接频率响应的计算速度快。
问题描述
对该件进行响应计算。
边界条件
一端孔固定,一端孔施加随时间变化的载荷。
材料参数
材料为铁材,单元厚度T=0.2mm,集中力F=sin(360*200*t)N。
分析结果
Mode
Displacement
29Hz
25Hz
Acceleration
25Hz
外部激励与系统在25Hz和
109Hz发生共振
卡片控制
GLOBAL_CASE_CONTROL 工况控制卡片设置
FREQ1扫描频率设置(起始频率1,间隔2,数目100)
TABDMP1阻尼设置
约束点
激励点
网格模型
RLOAD频率动态载荷设置
因为EXCITEID为DAREA或SPCD的编号,定义A;DELAY定义τ,当前取0;DPHASE定义θ,当前取0;TB为TABLEDi的编号,定义B(f);TP为TABLEDi的编号,定义Φ(f),当前取0;故
P(f)=A*B(f)
TABLED定义表函数
DAREA设置定义静态和动态载荷的比例(面积)
EIGRL模态求解设置
SOL求解卡片设置(模态频率响应分析)
PARAM输出文件控制
GLOBAL_OUTPUT_REQUEST输出结果数据控制。