承台斜截面受剪承载力计算公式
- 格式:doc
- 大小:33.00 KB
- 文档页数:5

60035500600120020782000355010001000混凝土强度等级:C35 1.573601950535616.7600016806kN-m26600mm 218000mm 215975kN-m25285mm 216068mm 228400kN480mm460mm 0.251.871338mm 0.690.950.90003276.74a0y = MIN((Sb- bc / 2 - bp/2),h0)= λ0y = a0y / ho =X方向上冲切系数β0y = 0.84 / (λ0y + 0.2)= 2*[β0x * (bc + a0y)+ β0y*(hc + a0x)] * βhp *ft * ho-Fl=圆桩换算桩截面边宽 bp = 0.8 * D = X方向上自柱边到最近桩边的水平距离: a0x = MIN((Sa- hc / 2 -bp / 2),h0) = λ0x = a0x / ho =X方向上冲切系数β0x = 0.84 / (λ0x + 0.2)= Y 方向上自柱边到最近桩边的水平距离:三、承台柱抗冲切验算:(1)第一冲切破坏锥体作用于冲切破坏锥体上的冲切力设计值:Fl = 8 * R =柱下矩形独立承台受柱冲切的承载力按下列公式计算Fl ≤ 2 * [β0x * (bc + a0y) + β0y * (hc + a0x)] * βhp *ft * ho桩径D(mm):柱子宽度bc(mm):单桩净反力设计值R(kN):承台边至桩中心的距离Sc(mm):基础埋深(m):桩列间距Sa(mm):桩行间距Sb(mm):最小配筋率ρmin =0.15% Asymin=Myct=2*R*(2*Sa-hc/2)+R*(Sa-hc/2)=二、承台受弯验算:(1) X 轴方向柱边的弯矩设计值:(绕X 轴)承台有效高度h 0(mm):承台宽度B(mm):(2) Y 轴方向柱边的弯矩设计值:(绕Y 轴)Mxct = 3 * R * (Sb - bc / 2)=钢筋面积(mm2): Asy=混凝土抗压强度fc(MPa):柱子高度hc(mm):钢筋面积(mm2): Asx=最小配筋率ρmin =0.15% Asxmin=混凝土抗拉强度ft(MPa):钢筋强度f y (MPa):一、基本资料:上式若>0即满足抗冲切要求;若<0即不满足抗冲切要求。


桩基承台的弯矩计算《建筑桩基技术规范》JGJ94-2008第5.9.2条指出:柱下独立桩基承台的正截面弯矩设计值可按下列规定计算:(1)两桩条形承台和多桩矩形承台弯矩计算截面取在柱边和承台变阶处,可按下列公式计算:M x=ΣN i y iM y=ΣN i x i式中:M x、M y——分别为绕x轴和绕y轴方向计算截面处的弯矩设计值(kN·m);xi、yi——垂直y轴和x轴方向自桩轴线到相应计算截面的距离(m);Ni——不计承台及其上土重,在荷载效应基本组合下的第i基桩或复合基桩竖向反力设计值(kN)。
《建筑桩基技术规范》JGJ94-2008第5.9.3条指出:箱形承台和筏形承台的弯矩可按下列规定计算:(1)箱形承台和筏形承台的弯矩宜考虑地基土层性质、基桩分布、承台和上部结构类型和刚度,按地基-桩-承台-上部结构共同作用原理分析计算;(2)对于箱形承台,当桩端持力层为基岩、密实的碎石类土、砂土且深厚均匀时;或当上部结构为剪力墙;或当上部结构为框架-核心筒结构且按变刚度调平原则布桩时,箱形承台底板可仅按局部弯矩作用进行计算;(3)对于筏形承台,当桩端持力层深厚坚硬、上部结构刚度较好,且柱荷载及柱间距的变化不超过20%时;或当上部结构为框架-核心筒结构且按变刚度调平原则布桩时,可仅按局部弯矩作用进行计算。
《建筑桩基技术规范》JGJ94-2008第5.9.4条指出:柱下条形承台梁的弯矩可按下列规定计算:(1)可按弹性地基梁(地基计算模型应根据地基土层特性选取)进行分析计算;(2)当桩端持力层深厚坚硬且桩柱轴线不重合时,可视桩为不动铰支座,按连续梁计算。
《建筑桩基技术规范》JGJ94-2008第5.9.5条指出:砌体墙下条形承台梁,可按倒置弹性地基梁计算弯矩和剪力,并应符合本规范附录G的要求。
对于承台上的砌体墙,尚应验算桩顶部位砌体的局部承压强度。
《建筑桩基技术规范》JGJ94-2008第5.9.6条指出:桩基承台厚度应满足柱(墙)对承台的冲切和基桩对承台的冲切承载力要求。

斜截面受剪承载力计算公式好的,以下是为您生成的关于“斜截面受剪承载力计算公式”的文章:在咱们建筑工程的世界里,斜截面受剪承载力计算公式那可是相当重要的“神器”。
就像我们出门得知道路线,做饭得清楚食材用量一样,搞建筑也得把这个公式弄明白。
我记得有一次,跟着一个施工队去现场考察。
那是一个阳光灿烂的日子,工地里机器轰鸣,工人们忙忙碌碌。
我们走到一处正在浇筑混凝土的地方,工程师拿着图纸,一脸严肃地和施工负责人讨论着什么。
我凑过去一听,原来他们在说斜截面受剪的问题。
工程师指着图纸上的一个部位说:“这个地方的斜截面受剪承载力可不能马虎,得严格按照公式来计算。
”施工负责人皱着眉头:“这公式太复杂了,我怕算错啊。
”工程师笑了笑:“别怕,咱们一步步来。
”这时候我才意识到,这个斜截面受剪承载力计算公式可不是摆在书本上的一堆符号,而是实实在在关系到建筑质量和安全的关键。
咱们先来聊聊这个公式到底是啥。
斜截面受剪承载力计算公式就像是一个精准的“天平”,它要平衡好多因素。
比如说混凝土的抗压强度、箍筋的抗拉强度、截面的尺寸,还有就是剪力的大小等等。
这可不是简单地把几个数字往里面一塞就行,每一个参数都有它的讲究。
就拿混凝土的抗压强度来说吧,它就像是建筑材料的“内功”,内功深厚,抵抗剪力的能力就强。
可别小看这抗压强度,它的数值可不是随便定的,得通过严格的实验和检测才能确定。
再说说箍筋。
箍筋就像是给建筑结构穿上的“铠甲”,它的抗拉强度直接影响着斜截面的受剪能力。
箍筋布置得合理、强度够高,就能在关键时刻发挥大作用,保护结构不被剪力破坏。
还有截面的尺寸,这就好比是一个容器的大小。
尺寸越大,能承受的剪力相对也就越大。
但也不是说越大就越好,还得考虑成本、空间等实际问题。
在实际应用这个公式的时候,那可得小心谨慎。
一个数字算错,可能就会带来大麻烦。
我曾经见过一个案例,就是因为计算时粗心大意,少考虑了一个因素,结果导致建筑在使用过程中出现了裂缝,这可把大家吓得不轻。

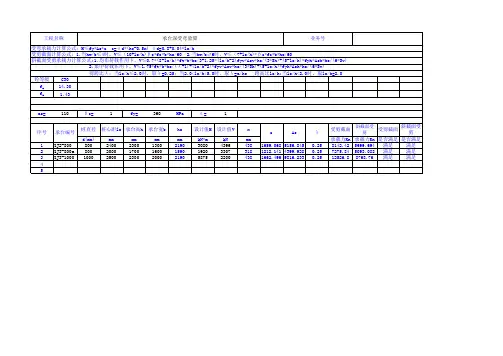

一.基本资料:承台类型:四桩承台圆桩直径d=400(mm)1200(mm)400(mm)1200(mm)1200(mm)柱子高度hc=500(mm)500(mm)65(mm)3014.3(N/mm 2) f t=1.43(N/mm 2)360(N/mm 2)11100(kN)0.15%1.3525(kN/m 3)1.3518(kN/m 3)1(m)0(kN)二.控制内力:Nk =4000(kN)M kx'=0(kN*m)Mky'=0(kN*m)V kx =0(kN)Vky=0(kN)F k =4000(kN)M kx =0(kN*m)Mky=0(kN*m)F=5400(kN)M x =(kN*m)My=(kN*m)a=2Sc+Sa=2(m)b=2Sc+Sb=2(m)4(m 2) 4.80(m 3)120.00(kN)67.50(kN)187.50(kN)四.承台验算:320(mm)1046.88≤ Ra =1100(kN)满足1046.88≤1.2*Ra=1320(kN)满足1046.88≤1.2*Ra=1320(kN)满足1046.88≤1.2*Ra=1320(kN)满足1046.88≤1.2*Ra=1320(kN)满足46.88(kN)1350.00(kN)1350.00(kN)Ni=F/n±Mxk*Yi/∑Yi 2±Myk*Xi/∑Xi 2(桩基规范 5.9.2-3)N1=F/4+Mx*Yi/∑Yi 2-My*Xi/∑Xi 2=N2=F/4+Mx*Yi/∑Yi 2+My*Xi/∑Xi 2=Qgk = Gk / 4 =扣除承台和其上土自重后的各桩桩顶相对于荷载效应基本组合的竖向力设计值:Q1k=(Fk+Gk)/4+Mxk*Yi/∑Yi 2-Myk*X i/∑Xi 2=Q2k=(Fk+Gk)/4+Mxk*Yi/∑Yi 2+Myk*X i/∑Xi 2=每根单桩所分配的承台自重和承台上土自重标准值Qgk:Q4k=(Fk+Gk)/4-Mxk*Yi/∑Yi 2+Myk*X i/∑Xi 2=承台上土的容重γs=⑴.单桩桩顶竖向力计算:最小配筋率=承台竖向附加荷载标准值Fk'=承台混凝土的容重γc= MKx=Mkx'-Vky*H、Mky=Mky'+Vkx*H《建筑桩基技术规范》(JGJ 94-2008),以下简称《桩基规范》 《钢筋混凝土承台设计规程》(CECS 88:97),以下简称《承台规程》 Fk=Nk+Fk'Fk-----------相应于荷载效应标准组合时,作用于基础顶面的竖向力值(kN)纵筋合力点至近边距离as=柱子宽度bc=设计时执行的规范:《建筑地基基础设计规范》(GB50007-2011),以下简称《地基规范》 《混凝土结构设计规范》(GB 50010-2010),以下简称《混凝土规范》构件重要性系数γ0=单桩竖向承载力设计值Ra=荷载的综合分项系数γz=永久荷载的分项系数γG=承台顶面以上土层覆土厚度ds=混凝土强度等级C钢筋强度设计值fy=fc=柱下独立承台承台根部高度H=桩行间距Sb=桩列间距Sa=承台边缘至桩心距离Sc=Nk-----------相应于荷载效应标准组合时,柱底轴向力值(kN)Vkx、Vky-----相应于荷载效应标准组合时,作用于基础顶面的剪力值(kN)Qk=(Fk+Gk)/4=Q3k=(Fk+Gk)/4-Mxk*Yi/∑Yi 2-Myk*X i/∑Xi 2=在偏心竖向力作用下:Qik=(Fk+Gk)/n±Mxk*Yi/∑Yi 2±M yk*X i/∑Xi 2在轴心竖向力作用下:承台及其上土自重标准值G k=Gk''+Gk'=圆桩换算桩截面边宽bp=0.8d=1.承台受弯计算:Mkx'、Mky'---相应于荷载效应标准组合时,作用于基础顶面的弯矩值(kN*m)Mkx、Mky-----相应于荷载效应标准组合时,作用于基础顶面的剪力值(kN*m)F、Mx、My----相应于荷载效应基本组合时,竖向力、弯矩设计值(kN、kN*m)(地基规范 8.5.4-2) F=γz*Fk、Mx=γz*Mkx、My=γz*Mky三.承台自重和承台上土自重标准值Gk:承台面积Ab=a*b=承台体积Vct=Ab*H=承台自重标准值G k''=γc*Vct=土自重标准值Gk'=γs*(Ab-bc*hc)*ds=。

承台计算公式的使用方法承台是工程中常用的一种基础结构形式,它承载着上部结构的荷载,并将荷载传递到地基土壤中。
在设计承台时,需要进行一系列的计算和分析,以确保其能够满足工程要求并保证结构的安全性。
在承台的设计计算中,公式的使用是非常重要的,下面将介绍承台设计中常用的计算公式及其使用方法。
1. 承台承载力计算公式。
承台的承载力是指其能够承受的最大荷载,通常包括承台的抗压承载力和抗剪承载力。
在计算承台的承载力时,可以使用以下公式:(1)承台的抗压承载力计算公式:Nc = φ Ac fc。
其中,Nc为承台的抗压承载力,φ为承载能力折减系数,Ac为承台的截面面积,fc为混凝土的抗压强度。
(2)承台的抗剪承载力计算公式:Vc = φ Av fv。
其中,Vc为承台的抗剪承载力,φ为承载能力折减系数,Av为承台的剪切面积,fv为混凝土的抗剪强度。
2. 承台的受力分析公式。
在进行承台的受力分析时,需要考虑承台受到的各种荷载及其作用,包括垂直荷载、水平荷载、弯矩等。
在进行受力分析时,可以使用以下公式:(1)承台受到的垂直荷载:P = ∑(Qi + Qs)。
其中,P为承台受到的总垂直荷载,Qi为上部结构的垂直荷载,Qs为承台自重。
(2)承台受到的水平荷载:H = ∑(Hi + Hs)。
其中,H为承台受到的总水平荷载,Hi为上部结构的水平荷载,Hs为其他水平荷载(如风荷载、地震荷载)。
(3)承台受到的弯矩:M = ∑(Mi + Ms)。
其中,M为承台受到的总弯矩,Mi为上部结构的弯矩,Ms为其他弯矩(如风载引起的弯矩)。
3. 承台的变形计算公式。
在设计承台时,需要考虑承台的变形情况,包括沉降、倾斜等。
在进行承台的变形计算时,可以使用以下公式:(1)承台的沉降计算公式:Δ = (P e) / (A E)。
其中,Δ为承台的沉降,P为承台受到的总垂直荷载,e为承台的弹性模量,A 为承台的截面积,E为地基土壤的弹性模量。
(2)承台的倾斜计算公式:θ = M / (A E)。

桥梁桩基承台的剪切及冲切计算摘要:本文通过对承台所受剪切力和冲切力的特征分析和比较对冲切和剪切的概念和具体验算的选择做进一步的说明,使我们更加明确剪切和冲切的概念和验算方法。
关键词:剪切;冲切;桩基承台一概述桥梁桩基承台是将桩基础和桥墩连接为整体的重要构件,通常结构是承台桩之上墩身以下的厚板,其作用为将桥梁上部荷载传递给桩基。
承台内部应力分布较为复杂,影响因素很多, 而在桩承台的计算中,各规范均明确要求同时验算剪切承载力和冲切承载力。
那么剪切和冲切有什么不同,各自验算方法又是什么呢?让我们试着分析一下。
目前国内桩基承台的计算方法,依据《公路钢筋混凝土预应力混凝土桥涵设计规范》JTG D62-2004(以下简称“新桥规”),“新桥规”承台冲切和剪切验算在原规范的基础上进行了一定的优化和修正,但是冲切和剪切的概念却并不明确,以至于许多同志对这两个概念还很模糊,那么下面我们就加以总结和区分。
二剪切和冲切的概念解析一般说来,柱下单独基础板双向受力,墙下条形基础板单向受力,冲切和剪切,其破坏机理类似,承载力均受混凝土的抗拉强度所控制。
不同的是剪切破坏面可视为平面,而冲切破坏面则可视为空间曲面,如截圆锥、截角锥或棱台及其他不规则曲面等。
故剪切又称单向剪切(one way sherar);冲切有时候也称冲剪,又称双向剪切(punching, two way shear)。
也就是说,两者相比,冲切是一个空间概念。
三剪切和冲切的区别我们还可以用小表来具体说明两者之间的异同:三具体验算方法抗剪验算“新桥规”中承台斜截面抗剪承载力是完全根据原规范混凝土的抗剪能力公式转化过来的,与普通受弯构件的混凝土抗剪公式(“新桥规”5.2.10式)相比,抗剪承载力有较大的提高,其原因是虽然两者都是根据同一公式得到的,但普通受弯构件的混凝土抗剪公式,是按剪跨比取3、纵向配筋率取2%~3%简化而来,对承台而言,由于剪跨比远小于3,虽然配筋也较上述数值小,但计算结果会比“新桥规”5.2.10式的计算结果大,而且一般情况下,随着跨高比的减少,梁的斜截面抗剪能力有一定的提高,承台的斜截面抗剪承载力的公式也符合该规律。
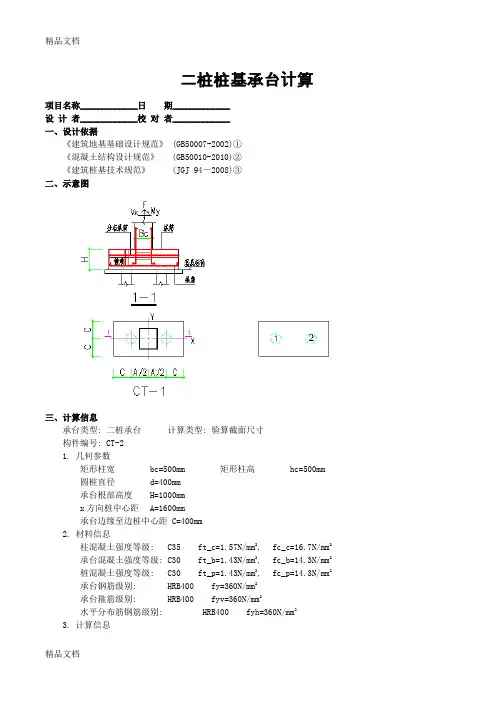
二桩桩基承台计算项目名称_____________日期_____________设计者_____________校对者_____________一、设计依据《建筑地基基础设计规范》 (GB50007-2002)①《混凝土结构设计规范》 (GB50010-2010)②《建筑桩基技术规范》 (JGJ 94-2008)③二、示意图三、计算信息承台类型: 二桩承台计算类型: 验算截面尺寸构件编号: CT-21. 几何参数矩形柱宽bc=500mm 矩形柱高hc=500mm圆桩直径d=400mm承台根部高度H=1000mmx方向桩中心距A=1600mm承台边缘至边桩中心距 C=400mm2. 材料信息柱混凝土强度等级: C35 ft_c=1.57N/mm2, fc_c=16.7N/mm2承台混凝土强度等级: C30 ft_b=1.43N/mm2, fc_b=14.3N/mm2桩混凝土强度等级: C30 ft_p=1.43N/mm2, fc_p=14.3N/mm2承台钢筋级别: HRB400 fy=360N/mm2承台箍筋级别: HRB400 fyv=360N/mm2水平分布筋钢筋级别: HRB400 fyh=360N/mm23. 计算信息结构重要性系数: γo=1.0纵筋合力点至近边距离: as=100mm4. 作用在承台顶部荷载基本组合值F=2490.600kNMx=4.800kN*mMy=3.100kN*mVx=5.500kNVy=23.800kN5. 配筋信息水平分布筋直径:12mm,间距:sv=100mm箍筋直径:12mm,间距:sh=100mm受拉筋最小配筋率:ρmin= 0.20%箍筋最小配筋率:ρsvmin= 0.20%水平分布筋最小配筋率:ρshmin= 0.20%箍筋面积:Asv=226mm2水平分布筋面积:Ash=226mm2四、计算参数1. 承台总长 Bx=C+A+C=0.400+1.600+0.400=2.400m2. 承台总宽 By=C+C=0.400+0.400=0.800m3. 承台根部截面有效高度 ho=H-as=1.000-0.100=0.900m4. 圆桩换算截面宽度 bp=0.8*d=0.8*0.400=0.320m五、内力计算1. 各桩编号及定位座标如上图所示:1号桩 (x1=-A/2=-0.800m, y1=0m)2号桩 (x2= A/2=0.800m, y2=0m)2. 各桩净反力设计值, 计算公式:N i=F/n+My*x i/∑x i2+Vx*H*x i/∑x i2【8.5.3-2】①N1=2490.600/2+3.100*(-0.800)/((-0.800)2*2)+5.500*1.000*(-0.800)/((-0.800)2*2) =1239.925kNN2=2490.600/2+3.100*0.800/(0.8002*2)+5.500*1.000*0.800/(0.8002*2)=1250.675kN六、承台斜截面受剪计算1. 得到承台底面处的最大剪力值V=γo*max(|N1|, |N2|)=1250.675kN2. 计算梁截面有效高度和腹板高度ho=H-as=1000-100=900mmhw=ho=900mm3. 确定跨高比lo =min(1.15*(A-ls),A)=1600mmlo/H=1600/1000=1.600<2.0, 取lo/H=2.000。
承台斜截面受剪承载力计算公式浅析摘要:《建筑地基基础设计规范》(GB50007-2002)第8.5.18条给出了承台的斜截面受剪承载力计算公式,该公式中承台计算截面处的计算宽度应按该规范附录S确定。
按附录S计算公式很长,不宜理解,使用不便。
笔者通过演算对承台的斜截面受剪承载力计算公式提出了自己的理解和概念明确的表达形式。
关键词:承台斜截面受剪承载力计算《建筑地基基础设计规范》(GB50007-2002)第8.5.18条规定:柱下桩基独立承台应分别对柱边和桩边、变阶处和桩边联线形成的斜截面进行受剪计算(图8.5.18)。
当柱边外有多排桩形成多个剪切斜截面时,尚应对每个斜截面进行计算。
斜截面受剪承载力可按下列公司计算:式中V 扣除承台及其上填土自重后相应于荷载效应基本组合时斜截面的最大剪力设计值;b0 承台计算截面处的计算宽度。
阶梯形承台变阶处的计算宽度、锥形承台的计算宽度应按本规范附录S确定;h0计算宽度处的承台有效高度β剪切系数βhs 受剪切承载力截面高度影响系数,按公式(8.4.5-4)计算λ计算截面的剪跨比,λx=,λy=。
ax、ay为柱边或承台变阶处至x、y方向计算一排桩的桩边的水平距离,当λ3时,取λ=3。
该规范附录S对阶梯形承台及锥形承台斜截面受剪的截面宽度规定如下:S.0.1对于阶梯形承台应分别在变阶处(A1—A1、B1—B1)及柱边处(A2—A2、B2—B2)进行斜截面受剪计算(图S.0.1)。
计算变阶处截面A1—A1、B1—B1的斜截面受剪承载力时,其截面有效高度均为h01,截面计算宽度分别为by1和bx1。
计算柱边截面A2—A2和B2—B2处的斜截面受剪承载力时,其截面有效高度均为h01+h02,截面计算宽度按下式计算:对A2—A2 by0 =(S.0.1-1)对B2—B2 bx0 =(S.0.1-2)S.0.2对于锥形承台应对A—A及B—B两个截面进行受剪承载力计算(图S.0.2),截面有效高度均为h0,截面的计算宽度按下式计算:对A—A by0 =by1 (S.0.2-1)对B—B bx0 =bx1(S.0.2-2)显然,上述(S.0.1-1)、(S.0.1-2)两个公式仅适用于阶梯形承台的阶数为二阶。
一.基本资料:承台类型:四桩承台圆桩直径d=400(mm)1200(mm)400(mm)1200(mm)1200(mm)柱子高度hc=500(mm)500(mm)65(mm)3014.3(N/mm 2) f t=1.43(N/mm 2)360(N/mm 2)11100(kN)0.15%1.3525(kN/m 3)1.3518(kN/m 3)1(m)0(kN)二.控制内力:Nk =4000(kN)M kx'=0(kN*m)Mky'=0(kN*m)V kx =0(kN)Vky=0(kN)F k =4000(kN)M kx =0(kN*m)Mky=0(kN*m)F=5400(kN)M x =(kN*m)My=(kN*m)a=2Sc+Sa=2(m)b=2Sc+Sb=2(m)4(m 2) 4.80(m 3)120.00(kN)67.50(kN)187.50(kN)四.承台验算:320(mm)1046.88≤ Ra =1100(kN)满足1046.88≤1.2*Ra=1320(kN)满足1046.88≤1.2*Ra=1320(kN)满足1046.88≤1.2*Ra=1320(kN)满足1046.88≤1.2*Ra=1320(kN)满足46.88(kN)1350.00(kN)1350.00(kN)Mkx'、Mky'---相应于荷载效应标准组合时,作用于基础顶面的弯矩值(kN*m)Mkx、Mky-----相应于荷载效应标准组合时,作用于基础顶面的剪力值(kN*m)F、Mx、My----相应于荷载效应基本组合时,竖向力、弯矩设计值(kN、kN*m)(地基规范 8.5.4-2) F=γz*Fk、Mx=γz*Mkx、My=γz*Mky三.承台自重和承台上土自重标准值Gk:承台面积Ab=a*b=承台体积Vct=Ab*H=承台自重标准值G k''=γc*Vct=土自重标准值Gk'=γs*(Ab-bc*hc)*ds=Nk-----------相应于荷载效应标准组合时,柱底轴向力值(kN)Vkx、Vky-----相应于荷载效应标准组合时,作用于基础顶面的剪力值(kN)Qk=(Fk+Gk)/4=Q3k=(Fk+Gk)/4-Mxk*Yi/∑Yi 2-Myk*X i/∑Xi 2=在偏心竖向力作用下:Qik=(Fk+Gk)/n±Mxk*Yi/∑Yi 2±M yk*X i/∑Xi 2在轴心竖向力作用下:承台及其上土自重标准值G k=Gk''+Gk'=圆桩换算桩截面边宽bp=0.8d=1.承台受弯计算:混凝土强度等级C钢筋强度设计值fy=fc=四桩承台计算书承台根部高度H=桩行间距Sb=桩列间距Sa=承台边缘至桩心距离Sc=纵筋合力点至近边距离as=柱子宽度bc=设计时执行的规范:《建筑地基基础设计规范》(GB50007-2011),以下简称《地基规范》 《混凝土结构设计规范》(GB 50010-2010),以下简称《混凝土规范》构件重要性系数γ0=单桩竖向承载力设计值Ra=荷载的综合分项系数γz=永久荷载的分项系数γG=承台顶面以上土层覆土厚度ds=承台上土的容重γs=⑴.单桩桩顶竖向力计算:最小配筋率=承台竖向附加荷载标准值Fk'=承台混凝土的容重γc= MKx=Mkx'-Vky*H、Mky=Mky'+Vkx*H《建筑桩基技术规范》(JGJ 94-2008),以下简称《桩基规范》 《钢筋混凝土承台设计规程》(CECS 88:97),以下简称《承台规程》 Fk=Nk+Fk'Fk-----------相应于荷载效应标准组合时,作用于基础顶面的竖向力值(kN)(桩基规范 5.9.2-3)N1=F/4+Mx*Yi/∑Yi 2-My*Xi/∑Xi 2=N2=F/4+Mx*Yi/∑Yi 2+My*Xi/∑Xi 2=Qgk = Gk / 4 =扣除承台和其上土自重后的各桩桩顶相对于荷载效应基本组合的竖向力设计值:Q1k=(Fk+Gk)/4+Mxk*Yi/∑Yi 2-Myk*X i/∑Xi 2=Q2k=(Fk+Gk)/4+Mxk*Yi/∑Yi 2+Myk*X i/∑Xi 2=每根单桩所分配的承台自重和承台上土自重标准值Qgk:Q4k=(Fk+Gk)/4-Mxk*Yi/∑Yi 2+Myk*X i/∑Xi 2= Ni=F/n±Mxk*Yi/∑Yi 2±Myk*Xi/∑Xi 2。
3、承台设计构造要求:承台最小宽度不应小于500mm,承台边缘至桩中心的距离不宜小于桩的直径或边长,边缘挑出部分不应小于150mm,墙下条形承台边缘挑出部分可降低至75mm。
条形和柱下独立承台的最小厚度为500mm,其最小埋深为600mm。
本工程中承台混凝土等级C30,取其中的(8)-(A)柱位置的承台为例计算:一、基本资料:承台类型:三桩承台圆桩直径d =500mm桩列间距Sa =900mm 桩行间距Sb =1560mm桩中心至承台边缘距离Sc =500mm承台根部高度H =1100mm 承台端部高度h =1100mm柱子高度hc =700mm(X 方向)柱子宽度bc =650mm(Y 方向)二、控制内力:Nk =4666;Fk =4666; F =6299.1;三、承台自重和承台上土自重标准值Gk:a =2(Sc + Sa) =2*(0.5+0.9) = 2.8mb =2Sc + Sb =2*0.5+1.56 =2.56m承台底部面积Ab =a * b - 2Sa * Sb / 2 = 2.8*2.56-2*0.9*1.56/2 = 5.76m承台体积Vct =Ab * H1 =5.76*1.1 =6.340m承台自重标准值Gk'' =γc * Vct =25*6.34 =158.5kN土自重标准值Gk' =γs * (Ab - bc * hc) * ds =18*(5.76-0.65*0.7)*0.8=76.4kN承台自重及其上土自重标准值Gk =Gk'' + Gk' =158.5+76.4 =235.0kN四、承台验算:圆桩换算桩截面边宽bp =0.866d =0.866*500 =433mm1、承台受弯计算:(1)、单桩桩顶竖向力计算:在轴心竖向力作用下Qk =(Fk + Gk) / n (基础规范8.5.3-1)Qk =(4666+235)/3 =1633.7kN ≤ Ra =2020kN每根单桩所分配的承台自重和承台上土自重标准值Qgk:Qgk =Gk / n =235/3 =78.3kN扣除承台和其上填土自重后的各桩桩顶相应于荷载效应基本组合时的竖向力设计值:Ni =γz * (Qik - Qgk)N =1.35*(1633.7-78.3) =2099.7kN(2)、承台形心到承台两腰的距离范围内板带的弯矩设计值:S =(Sa ^ 2 + Sb ^ 2) ^ 0.5 =(0.9^2+1.56^2)^0.5 =1.801mαs =2Sa =2*0.9 =1.800mα =αs / S =1.8/1.801 =0.999承台形心到承台两腰的距离B1:B1 =Sa / S * 2Sb / 3 + Sc * (Sa + Sb) / S =1.203mM1 =Nmax * [S - 0.75 * c1 / (4 - α ^ 2) ^ 0.5] / 3(基础规范8.5.16-4)=2099.7*[1.801-0.75*0.65/(4-0.999^2)^0.5]/3=1063.6kN·m②号筋Asy =3783mmζ =0.068 ρ =0.32%10Φ22@110(As =3801)(3)、承台形心到承台底边的距离范围内板带的弯矩设计值:承台形心到承台底边的距离B2 =Sb / 3 + Sc =1.020mM2 =Nmax * [αs - 0.75 * c2 / (4 - α ^ 2) ^ 0.5] / 3(基础规范8.5.16-5)=2099.7*[1.8-0.75*0.7/(4-0.999^2)^0.5]/3=1047.7kN·m①号筋Asx =3667mmζ =0.076 ρ =0.36%10Φ22@100(As =3801)2、承台受冲切承载力验算:(1)、柱对承台的冲切验算:扣除承台及其上填土自重,作用在冲切破坏锥体上的冲切力设计值:Fl =6299100N三桩三角形柱下独立承台受柱冲切的承载力按下列公式计算:Fl ≤ [βox * (2bc + aoy1 + aoy2) + (βoy1 + βoy2) * (hc + aox)] * βhp * ft *ho(参照承台规程4.2.1-2)X 方向上自柱边到最近桩边的水平距离:aox =900 - 0.5hc - 0.5bp =900-700/2-433/2 =333mmλox =aox / ho =333/(1100-110) =0.337X 方向上冲切系数βox =0.84 / (λox + 0.2)(基础规范8.5.17-3)βox =0.84/(0.337+0.2) =1.565Y 方向(下边)自柱边到最近桩边的水平距离:aoy1 =2 * 1560 / 3 - 0.5bc - 0.5bp =1040-650/2-433/2 =498mmλoy1 =aoy1 / ho =498/(1100-110) =0.504Y 方向(下边)冲切系数βoy1 =0.84 / (λoy1 + 0.2)(基础规范8.5.17-4)βoy1 =0.84/(0.504+0.2) =1.194Y 方向(上边)自柱边到最近桩边的水平距离:aoy2 =1560 / 3 - 0.5bc - 0.5bp =520-650/2-433/2 =-22mmλoy2 =aoy2 / ho =-22/(1100-110) =-0.022当λoy2 < 0.2 时,取λoy2 =0.2,aoy2 =0.2ho =0.2*990 =198mmY 方向(上边)冲切系数βoy2 =0.84 / (λoy2 + 0.2)(基础规范8.5.17-4)βoy2=0.84/(0.2+0.2) =2.1[βox * (2bc + aoy1 + aoy2) + (βoy1 + βoy2) * (hc + aox)] * βhp * ft * ho=[1.565*(2*650+498+198)+(1.194+2.1)*(700+333)]*0.975*1.43*990=9029023N ≥ Fl=6299100N,满足要求。
承台斜截面受剪承载力计算公式浅析摘要:《建筑地基基础设计规范》(gb50007-2002)第8.5.18条给出了承台的斜截面受剪承载力计算公式,该公式中承台计算截面处的计算宽度应按该规范附录s确定。
按附录s计算公式很长,不宜理解,使用不便。
笔者通过演算对承台的斜截面受剪承载力计算公式提出了自己的理解和概念明确的表达形式。
关键词:承台斜截面受剪承载力计算
《建筑地基基础设计规范》(gb50007-2002)第8.5.18条规定:柱下桩基独立承台应分别对柱边和桩边、变阶处和桩边联线形成的斜截面进行受剪计算(图8.5.18)。
当柱边外有多排桩形成多个剪切斜截面时,尚应对每个斜截面进行计算。
斜截面受剪承载力可按下列公司计算:
式中 v 扣除承台及其上填土自重后相应于荷载效应基本组合
时斜截面的最大剪力设计值;
b0 承台计算截面处的计算宽度。
阶梯形承台变阶处的计算宽度、锥形承台的计算宽度应按本规范附录s确定;
h0计算宽度处的承台有效高度
β剪切系数
βhs 受剪切承载力截面高度影响系数,按公式(8.4.5-4)计算
λ计算截面的剪跨比,λx=,λy=。
ax、ay为柱边或承台变阶处至x、y方向计算一排桩的桩边的水平距离,当λ3时,取λ=3。
该规范附录s对阶梯形承台及锥形承台斜截面受剪的截面宽度规定如下:
s.0.1对于阶梯形承台应分别在变阶处(a1—a1、b1—b1)及柱边处(a2—a2、b2—b2)进行斜截面受剪计算(图s.0.1)。
计算变阶处截面a1—a1、b1—b1的斜截面受剪承载力时,其截面有效高度均为h01,截面计算宽度分别为by1和bx1。
计算柱边截面a2—a2和b2—b2处的斜截面受剪承载力时,其截面有效高度均为h01+h02,截面计算宽度按下式计算:对a2—a2 by0 =(s.0.1-1)
对b2—b2 bx0 =(s.0.1-2)
s.0.2对于锥形承台应对a—a及b—b两个截面进行受剪承载力计算(图s.0.2),截面有效高度均为h0,截面的计算宽度按下式计算:
对a—a by0 =by1 (s.0.2-1)
对b—b bx0 =bx1(s.0.2-2)
显然,上述(s.0.1-1)、(s.0.1-2)两个公式仅适用于阶梯形承台的阶数为二阶。
对多于二阶的情况,规范没有交代。
《建筑桩基技术规范》(jgj94-2008)第5.9.10条给出的计算
方法与上述一致。
上面计算b0的公式,都很长,符号较多,咋一看,不易理解,也不易记忆,使用起来也不方便。
有没有一种便于理解记忆的表达形式呢?为此,我们将b0与h0联合起来考查。
按s.0.1条规定,阶梯形承台计算柱边截面a2—a2和b2—b2处的斜截面受剪承载力时,其截面有效高度均为h01+h02。
我们将公式(s.0.1-1)、(s.0.1-2)的等号两边同乘以(h01+h02),即对a2—a2 by0 ·(h01+h02)= (h01+h02)
= by1·h01 + by2·h02
=s y向下阶有效截面积 + s y向上阶截面积
= s y向有效横截面面积
对b2—b2 bx0 ·(h01+h02)= (h01+h02)
= by1·h01 + by2·h02
=s x向下阶有效截面积 + s x向上阶截面积
= s x向有效横截面面积
按s.0.2条规定,锥形承台计算a—a及b—b两个截面的斜截面受剪承载力时,截面有效高度均为h0。
我们将公式(s.0.2-1)、(s.0.2-2)的等号两边同乘以h0,即
对a—a by0·h0 =by1·h0
= by1·h0 — 0.5··by1·h0
= by1·h0 — 0.5h1(by1-by2)
= by1·h0 — 2··h1·
= s y向大矩形有效截面积— 2·s y向三角形截面积
= s y向有效横截面面积
对b—b bx0·h0 =bx1·h0
= bx1·h0 — 0.5··bx1·h0
= bx1·h0 — 0.5h1(bx1-bx2)
= bx1·h0 — 2··h1·
= s x向大矩形有效截面积— 2·s x向三角形截面积
= s x向有效横截面面积
可见,承台斜截面受剪承载力计算公式(8.5.18-1)中,
b0h0 = 承台计算截面处的计算宽度x计算宽度处的承台有效高度
= 承台计算截面处按有效高度计算的横截面面积(可简称为计算截面处有效横截面面积,见示意图)
令承台计算截面处按有效高度计算的横截面面积为a0,则有
b0h0= a0。
公式(8.5.18-1)则可改为v≤βhsβfta0
公式(8.5.18-1)中引入a0后,可以跳过计算宽度的计算,直接计算有效横截面面积。
因为横截面面积的计算方法多种多样,可以视个人习惯和具体工程情况由计算者选定。
另一方面,引入a0后可以囊括各种横截面形式(无论规则或不规则),承台阶数也不再
局限于二阶。
综上所述,笔者建议国家规范在修订时对承台斜截面受剪承载力计算公式进行调整,使其概念更清晰,计算更方便,适用范围更广。
调整方案如下:
1、公式(8.5.18-1)改为v≤βhsβfta0,a0指承台计算截面处按有效高度计算的横截面面积。
其他符号不变。
2.删除附录s对阶梯形承台及锥形承台斜截面受剪的截面宽度计算规定。
注:文章内的图表、公式请到pdf格式下查看。