代几综合题复习10页

2024中考二次函数代几综合题变式训练大全一、概述在中学数学教学中，二次函数是一个重要的数学知识点。

在中考中，二次函数常常作为考查的重点内容。

而对于学生来说，掌握二次函数的各种变式训练是非常重要的。

本文就收集整理了2024中考二次函数代几综合题变式训练大全，希望能够帮助学生更好地备战中考。

二、二次函数基础知识复习我们先来复习一下二次函数的基础知识。

二次函数一般的标准形式为：f(x)=ax^2+bx+c，其中a、b、c为常数且a≠0。

这是一个抛物线的标准方程，其中a决定了抛物线的开口方向，b决定了抛物线在x轴上的位置，c决定了抛物线在y轴上的位置。

除了标准形式以外，二次函数还有其他几种重要的变式形式，比如顶点形式、交点形式等。

在解题时，需要根据具体的题目情况选择合适的形式进行运算。

三、二次函数代几综合题变式训练接下来，我们将列举一些2024中考二次函数代几综合题的变式训练。

这些题目包括了二次函数的各种形式，涵盖了中考可能会考查的各种情况。

希望同学们可以认真对待这些训练题，加强对二次函数知识的理解和应用。

1.简单题目已知二次函数f(x)=2x^2+3x-5，求f(1)的值。

2.顶点形式已知二次函数f(x)=a(x-h)^2+k的顶点为V(2,3)，且经过点P(1,4)，求a的值。

3.交点形式已知二次函数f(x)=ax^2+bx的图象与x轴交于A(-2,0)、B(3,0)，且经过点P(1,6)，求a、b的值。

4.与直线交点已知二次函数f(x)=x^2-3x+2与直线y=2x-5有交点C，求C的坐标。

5.二次函数图象已知二次函数f(x)=ax^2+bx+c的图象过点A(1,4)、B(2,3)、C(3,0)，求a、b、c的值。

6.利用二次函数解实际问题某商品售价为x元，销量为f(x)=200-2x，求最高售价及对应的销量，求销售收入的最大值。

以上就是一些简单的二次函数综合题的变式训练，希望同学们通过这些题目的练习，能够更熟练地掌握二次函数的相关知识。

❖ 当函数与几何图形相结合时，关键是要做好点的 坐标与线段长的互相转化，同时还要考虑分类讨 论．
❖ 分类讨论是要依据一定的标准，对问题分类、求 解，要特别注意分类原则是不重不漏、最简.
分类常见的依据是：
❖ 一是依概念分类，如判断直角三角形时明确哪个角 可以是直角，两个三角形相似时分清谁与谁可以是 对应角；
在中考试卷中，代成.
► 热考一 坐标系中的几何问题
❖ 本类题通常先给定函数解析式和几何图形，由几何 图形的性质或解析法确定待定系数所需的条件，求 出函数解析式，然后根据所求的函数关系进行探索 研究．探索研究的一般类型有：①在什么条件下三 角形是等腰三角形、直角三角形；②四边形是菱形、 梯形等；③探索两个三角形满足什么条件相似；④ 探究线段之间的位置关系等．
❖ 二是依运动变化的图形中的分界点进行分类，如一 个图形在运动过程中，与另一个图形重合部分可以 是三角形，也可以是四边形、五边形等；
❖ 三是依据图形间的位置关系，如点在线段上(不与端 点重合)、点与端点重合、点在线段延长线上等．
► 热考二 动点问题
❖ 解决动态几何问题我们需要用运动与变化的 眼光去观察和研究图形，把握图形运动与变 化的全过程，抓住其中的等量关系和变量关 系，并特别关注一些不变量和不变关系或特 殊关系；在求有关图形的变量之间关系时， 通常建立函数模型或不等式模型来求解；求 图形之间的特殊数量关系和一些特殊值时， 通常建立方程模型求解
二、应用举例 [2012·北京]
在平面直角坐标系 xOy 中，抛物线 y＝－m－4 1x2＋54mx＋m2－3m ＋2 与 x 轴的交点分别为原点 O 和点 A，点 B(2，n)在这条抛物线上.
(1) 求 B 点的坐标；(2) 点 P 在线段 OA 上，从 O 点出发向 A 点 运动，过 P 点作 x 轴的垂线，与直线 OB 交于点 E，延长 PE 到点 D，

代几综合题（以代数为主的综合）知识梳理教学重、难点作业完成情况典题探究例1 已知抛物线c bx ax y ++=2与y 轴交于点A （0，3），与x 轴分别交于B （1，0）、C （5，0）两点．（1）求此抛物线的解析式；（2）若点D 为线段OA 的一个三等分点, 求直线DC 的解析式；（3）若一个动点P 自OA 的中点M 出发，先到达x 轴上的某点（设为点E ），再到达抛物线的对称轴上某点（设为点F ），最后运动到点A ，求使点P 运动的总路径最短的点E 、点F 的坐标，并求出这个最短总路径的长．例2 在平面直角坐标系xOy 中，抛物线2y mx n =++经过(02)P A ，两点． （1）求此抛物线的解析式；（2）设抛物线的顶点为B ，将直线AB 沿y 轴向下平移两个单位得到直线，直线与抛物线的对称轴交于C 点，求直线的解析式；（3）在（2）的条件下，求到直线OB OC BC ，，距离相等的点的坐标．例3在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A 、B 两点（点A 在点B的左侧．．），与y 轴交于点C ，点B 的坐标为（3，0），将直线y kx =沿y 轴向上平移 3个单位长度后恰好经过B 、C 两点．（1） 求直线BC 及抛物线的解析式；（2）设抛物线的顶点为D ，点P 在抛物线的对称轴上，且∠APD =∠ACB ，求点P的坐标；（3）连结CD ，求∠OCA 与∠OCD 两角和的度数．例4在平面直角坐标系xOy 中，抛物线23454122+-++--=m m x m x m y 与x 轴的交点分别为原点O 和点A ，点B(2，n)在这条抛物线上.(1) 求点B 的坐标；(2) 点P 在线段OA 上，从O 点出发向点运动，过P 点作x 轴的垂线，与直线OB 交于点E 。

延长PE 到点D 。

使得ED=PE. 以PD 为斜边在PD 右侧作等腰直角三角形PCD(当P 点运动时，C 点、D 点也随之运动)当等腰直角三角形PCD 的顶点C 落在此抛物线上时，求OP 的长；若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位(当Q 点到达O 点时停止运动，P 点也同时停止运动)。

专题10 代几综合题中的新定义目录【题型一】 二次函数中的新定义【典例分析】﹣x，其顶点（2023青浦区一模）在平面直角坐标系xOy中（如图），已知抛物线y＝x22为A．（1）写出这条抛物线的开口方向、顶点A的坐标；（2）我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”．①试求抛物线y＝x22﹣x的“不动点”的坐标；②向左或向右平移抛物线y＝x22﹣x，使所得新抛物线的顶点B是该抛物线的“不动点”，其对称轴与x轴交于点C，且四边形OABC是梯形，求新抛物线的表达式．【分析】（1）∵a＝1＞0，故该抛物线开口向上，顶点A的坐标为（1，﹣1）；﹣t，即可求解；（2）①设抛物线“不动点”坐标为（t，t），则t＝t22②新抛物线顶点B为“不动点”，则设点B（m，m），则新抛物线的对称轴为：x＝m，与x轴的交点C（m，0），四边形OABC是梯形，则直线x＝m在y轴左侧，而点A （1，﹣1），点B （m ，m ），则m ＝﹣1，即可求解．【解答】解：（1）∵a ＝1＞0，y ＝x 22﹣x ＝（x 1﹣）21﹣故该抛物线开口向上，顶点A 的坐标为（1，﹣1），（2）①设抛物线“不动点”坐标为（t ，t ），则t ＝t 22﹣t ，解得：t ＝0或3，故“不动点”坐标为（0，0）或（3，3）；②当OC ∥AB 时，∵新抛物线顶点B 为“不动点”，则设点B （m ，m ），∴新抛物线的对称轴为：x ＝m ，与x 轴的交点C （m ，0），∵四边形OABC 是梯形，∴直线x ＝m 在y 轴左侧，∵BC 与OA 不平行，∴OC ∥AB ，又∵点A （1，﹣1），点B （m m ），∴m ＝﹣1，故新抛物线是由抛物线y ＝x 22﹣x 向左平移2个单位得到的；当OB ∥AC 时，同理可得：抛物线的表达式为：y ＝（x 2﹣）2+2＝x 24﹣x +6，当四边形OABC 是梯形，字母顺序不对，故舍去，综上，新抛物线的表达式为：y ＝（x +1）21﹣．【点评】本题为二次函数综合运用题，正确利用二次函数基本知识、梯形基本性质进行分析是解题关键．【提分秘籍】所谓“新定义”型问题，主要是指在问题中定义了初中数学中没有学过的一些概念、新运算、新符号，要求同学们读懂题意并结合已有知识、能力进行理解，根据新定义进行运算、推理、迁移的一种题型。

专题五 2012年一模 代几综合题一、因动点特殊情况产生相似【例1】 （石景山）已知二次函数)34()22(22-+++-=m m x m x y 中，m 为不小于0的整数，它的图像与x 轴交于点A 和点B ，点A 在原点左边，点B 在原点右边． （1）求这个二次函数的解析式；（2）点C 是抛物线与y 轴的交点，已知AD=AC （D 在线段AB 上），有一动点P 从点A 出发，沿线段AB 以每秒1个单位长度的速度移动，同时，另一动点Q 从点C 出发，以某一速度沿线段CB 移动，经过t 秒的移动，线段PQ 被CD 垂直平分，求t 的值； （3）在（2）的情况下，求四边形ACQD 的面积．二、动点产生图形【例2】 （延庆） 在平面直角坐标系xOy 中，已知二次函数213y ax x c =++的图像经过原点及点1,2A （），与x 轴相交于另一点B 。

（1）求：二次函数1y 的解析式及B 点坐标；（2）若将抛物线1y 以x=3为对称轴向右翻折后，得到一个新的二次函数2y ,已知二次函数2y 与x 轴交于两点，其中右边的交点为C 点. 点P 在线段OC 上，从O 点出发向C 点运动，过P 点作x 轴的垂线，交直线AO 于D 点，以PD 为边在PD 的右侧作正方形PDEF （当P 点运动时，点D 、点E 、点F 也随之运动）； ①当点E ②若点P 从O 出发向O 运动）。

过Q 点作x 运动时，点G 、点M三、简单几何最值+面积问题【例3】 （昌平） 如图，已知抛物线2y ax bx c =++与x 轴交于A （-1，0）、B （3，0）两点，与y 轴交于点C （0，3）．（1）求抛物线的解析式及顶点M 坐标；（2）在抛物线的对称轴上找到点P ，使得△PAC 的周长最小，并求出点P 的坐标； （3）若点D 是线段OC 上的一个动点（不与点O 、C 重合）．过点D 作DE ∥PC 交x 轴于点E ．设CD 的长为m ，问当m 取何值时，1S S 9PDEABMC =四边形．四、坐标系内等面积问题【例4】 （顺义）如图，在平面直角坐标系xOy 中，抛物线22y mx mx n =++经过点A （−4，0）和点B （0，3）．（1）求抛物线的解析式；（2）向右平移上述抛物线，若平移后的抛物线仍经过点B ，求平移后抛物线的解析式；（3）在（2）的条件下，记平移后点A 的对应点为A’，点B 的对应点为B’，试问：在平移后的抛物线上是否存在一点P ，使'OA P △的面积与四边形AA’B’B 的面积相等，若存在，求出点P 的坐标；若不存在，说明理由．五、坐标系内特殊三角形、四边形与相似【例5】 （房山）如图⑴，在平面直角坐标系中，O 为坐标原点，抛物线28166y ax ax a =＋＋＋经过点B （0，4）.⑴求抛物线的解析式；⑵设抛物线的顶点为D ，过点D 、B 作直线交x 轴于点A ，点C 在抛物线的对称轴上，且C 点的纵坐标为-4，联结BC 、AC.求证：△ABC 是等腰直角三角形；⑶在⑵的条件下，将直线DB 沿y 轴向下平移，平移后的直线记为l ，直线l 与x 轴、y 轴分别交于点A B ''、，是否存在直线l ，使A B C ''是直角三角形，若存在求出l 的解析式，若不存在，请说明理由．图⑴ 备用图【例6】 （门头沟）在平面直角坐标系中，二次函数322-+=x x y 的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），交y 轴于点E .点C 是点A 关于点B 的对称点，点F 是线段BC 的中点，直线l 过点F 且与y 轴平行. 一次函数y=－x ＋m 的图象过点C ，交y 轴于D 点. （1）求点C 、点F 的坐标；（2）点K 为线段AB 上一动点，过点K 作x 轴的垂线与直线CD 交于点H ，与抛物线交于点G ，求线段HG 长度的最大值；（3）在直线l 上取点M ，在抛物线上取点N ，使以点A ，C ，M ，N 为顶点的四边形是平行四边形，求点N 的坐标.【例7】 （朝阳）在平面直角坐标系xOy 中，抛物线23y ax bx =++经过点N （2,－5），过点N 作x 轴的平行线交此抛物线左侧于点M ，MN =6. （1）求此抛物线的解析式；（2）点P （x,y ）为此抛物线上一动点，连接MP 交此抛物线的对称轴于点D ，当△DMN 为直角三角形时，求点P 的坐标；（3）设此抛物线与y 轴交于点C ，在此抛物线上是否存在点Q ，使∠QMN =∠CNM ？若存在，求出点Q 的坐标；若不存在，说明理由.【例8】 （怀柔）如图1，已知抛物线的顶点为A （2，1），且经过原点O ，与x 轴的另一个交点为B ． （1）求抛物线的解析式；（2）若点C 在抛物线的对称轴上，点D 在抛物线上，且以O C D B ，，，四点为顶点的四边形为平行四边形，求D 点的坐标；（3）连接OA ，AB ，如图2，在x 轴下方的抛物线上是否存在点P ，使得OBP △与OAB △相似？若存在，求出P 点的坐标；若不存在，说明理由．【例9】（燕山）已知点11,2A⎛⎫⎪⎝⎭在抛物线213y x bx c=++上，点11,22F⎛⎫-⎪⎝⎭在它的对称轴上，点P为抛物线上一动点.（1）求这条抛物线的函数解析式；（2）判断是否存在直线l，使得线段PF的长总是等于点P到直线l的距离，需说明理由.（3）设直线PF与抛物线的另一交点为Q，探究：PF和QF这两条线段的倒数和是否为定值？证明你的结论.六、轴对称问题【例10】 （密云）已知：在平面直角坐标系xoy 中，抛物线245y ax x =++过点A （－1，0），对称轴与x 轴交于点C ，顶点为B ． （1）求a 的值及对称轴方程；（2）设点P 为射线BC 上任意一点（B 、C 两点除外），过P 作BC 的垂线交直线AB 于点D ，连结PA ．设△APD 的面积为S ，点P 的纵坐标为m ，求S 与m 的函数关系式，并写出自变量m 的取值范围；（3）设直线AB 与y 轴的交点为E ，如果某一动点Q 从E 点出发，到抛物线对称轴上某点F ，再到x 轴上某点M ，从M 再回到点E ．如何运动路径最短？请在直角坐标系中画出最短路径，并写出点M 的坐标和运动的最短距离．【例11】（丰台）已知：如图，在平面直角坐标系xOy 中，以点()23P ，为圆心的圆与y 轴相切于点A ，与x 轴相交于B 、C 两点（点B 在点C 的左边）． （1）求经过A 、B 、C 三点的抛物线的解析式；（2）在（1）中的抛物线上是否存在点M ，使△MBP 的面积是菱形ABCP 面积的21．如果存在，请直接写出所有满足条件的M 点的坐标；如果若不存在，请说明理由；（3）如果一个动点D 自点P 出发，先到达y 轴上的某点，再到达x 轴上某点，最后运动到（1）中抛物线的顶点Q 处，求使点D 运动的总路径最短的路径的长．【例12】 （东城）如图，在平面直角坐标系xOy 中,二次函数232y x bx c =++的图象与x 轴交于1,03,0A B -（）、（）两点, 顶点为C . (1) 求此二次函数解析式；(2) 点D 为点C 关于x 轴的对称点，过点A 作直线l ：3333y x =+交BD 于点E ，过点B 作直线BK ∥AD 交直线l 于K 点.问：在四边形ABKD 的内部是否存在点P ，使得它到四边形ABKD四边的距离都相等，若存在，请求出点P 的坐标；若不存在，请说明理由； (3) 在（2）的条件下，若M 、N 分别为直线AD 和直线l 上的两个动点，连结DN 、NM 、MK ，求DN NM MK ++和的最小值.【例13】（西城）平面直角坐标系xOy 中，抛物线244y ax ax a c =-++与x 轴交于点A 、点B ，与y 轴的正半轴交于点C ，点A 的坐标为(1,0)，OB =OC ，抛物线的顶点为D ． (1) 求此抛物线的解析式；(2) 若此抛物线的对称轴上的点P 满足∠APB =∠ACB ，求点P 的坐标；(3) Q 为线段BD 上一点，点A 关于∠AQB 的平分线的对称点为A '，若2=-QB QA ，求点Q 的坐标和此时△QAA '的面积．【例14】 （大兴）在平面直角坐标系xOy 中，O 为坐标原点，直线)0,2121(332≠≤≤-+=k k m kx y 其中经过点()A ,且与y 轴相交于点C .点B 在y 轴上，且7OB OA =+-. △ABC 的面积为S . （1）求m 的取值范围; （2）求S 关于m 的函数关系式;（3）设点B 在y 轴的正半轴上，当S 取得最大值时，将△ABC 沿AC 折叠得到C B A '∆，求点B '的坐标.七、平面解析几何思想渗透【例15】（海淀）已知抛物线2y x bx c =++的顶点为P ，与y 轴交于点A ，与直线OP 交于点B .（1）如图1，若点P 的横坐标为1，点B 的坐标为（3，6），试确定抛物线的解析式；（2）在（1）的条件下，若点M 是直线AB 下方抛物线上的一点，且3ABM S ∆=, 求点M 的坐标； （3）如图2，若点P 在第一象限，且PA =PO ，过点P 作PD ⊥x 轴于点D . 将抛物线2y x bx c =++平移，平移后的抛物线经过点A 、D ，该抛物线与x 轴的另一个交点为C ，请探究四边形OABC 的形状，并说明理由.【例16】（平谷）已知抛物线2142y x bx =-++上有不同的两点2(3,1)E k k +-+和 2(1,1)F k k ---+（2k ≠-）．（1）求抛物线的解析式． （2）如图，抛物线2142y x bx =-++与x 轴和y 轴的正半轴分别交于点A 和B ，M 为AB 的中点，∠PMQ 在AB 的同侧以M 为中心旋转，且∠PMQ ＝45°，MP 交y 轴于点C ，MQ 交x 轴于点D ．设AD 的长为m （m ＞0），BC 的长为n ，求n 和m 之间的函数关系式．(3)当m ，n 为何值时，∠PMQ 的边过点F ．BAMCDOPQxy【例17】（通州）已知：如图，二次函数()214y a x =+－的图象与x 轴分别交于A 、B 两点，与y 轴交于点D ，点C 是二次函数()214y a x =+－的图象的顶点，2CD =（1）求a 的值.（2）点M 在二次函数()214y a x =+－图象的对称轴上，且∠AMC =∠BDO ，求点M 的坐标． （3）将二次函数()214y a x =+－的图象向下平移0k k （＞）个单位，平移后的图象与直线CD 分别交于E 、F 两点（点F 在点E 左侧），设平移后的二次函数的图象的顶点为1C ，与y 轴的交点为1D ，是否存在实数k ，使得1CF FC ⊥，若存在，求出k 的值；若不存在，请说明理由．。

代几综合与动手操作集锦（一）1、如图，M 为线段AB 的中点，AE 与BD 交于点C ，∠DME ＝∠A ＝∠B ＝α，且DM 交AC 于F ，ME 交BC 于G ． （1）写出图中三对相似三角形，并证明其中的一对；（2）连结FG ，如果α＝45°，AB＝AF ＝3，求FG 的长．2、如图，直角梯形ABCD 中，AD ∥BC ，∠ABC ＝90°，已知AD ＝AB ＝3，BC ＝4，动点P 从B 点出发，沿线段BC 向点C 作匀速运动；动点Q 从点D 出发，沿线段DA 向点A 作匀速运动．过Q 点垂直于AD 的射线交AC 于点M ，交BC 于点N ．P 、Q 两点同时出发，速度都为每秒1个单位长度．当Q 点运动到A 点，P 、Q 两点同时停止运动．设点Q 运动的时间为t 秒．(1)求NC ，MC 的长(用t 的代数式表示)；(2)当t 为何值时， 四边形PCDQ 构成平行四边形？(3)是否存在某一时刻，使射线 QN 恰好将△ABC 的面积和周长同时平分？若存在，求出此时t 的值； 若不存在，请说明理由；(4)探究：t 为何值时，△PMC 为等腰三角形？3、如图，在边长为5的正方形中，点、分别是、边上的点，且，延长交正方形外角平分线，边上是否存在一点，使得四边形是平行四边形？若存在，请给予证明；若不存在，请说明理由．ABCD E F BC DC AE EF EF CP P 于点AB MDMEP4、如图（1），抛物线22y x x k =-+与x 轴交于A 、B 两点，与y 轴交于点C （0，3-）． ［图（2）、图（3）为解答备用图］（1）k = ，点A 的坐标为 ，点B 的坐标为 ； （2）设抛物线22y x x k =-+的顶点为M ，求四边形ABMC 的面积；（3）在x 轴下方的抛物线上是否存在一点D ，使四边形ABDC 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；（4）在抛物线22y x x k =-+上求点Q ，使△BCQ 是以BC 为直角边的直角三角形．5、已知：如图所示，直线MA NB MAB ∠∥，与NBA ∠的平分线交于点C ，过点C 作一条直线l 与两条直线MA NB 、分别相交于点D E 、．（1）如图1所示，当直线l 与直线MA 垂直时，猜想线段AD BE AB 、、之间的数量关系，请直接写出结论，不用证明；（2）如图2所示，当直线l 与直线MA 不垂直且交点D E 、都在AB 的同侧时，（1）中的结论是否成立？如果成立，请证明：如果不成立，请说明理由；（3）当直线l 与直线MA 不垂直且交点D E 、在AB 的异侧时，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，那么线段AD BE AB 、、之间还存在某种数量关系吗？如果存在，请直接写出它们之间的数量关系．图（1） 图（2） 图（3）ABED CM NABED CM N l ABCM NABCM N图1图2备用图备用图6、如图所示，在△ABC 中，D 、E 分别是AB 、AC 上的点，DE ∥BC ，如图①，然后将△ADE 绕A 点顺时针旋转一定角度，得到图②，然后将BD 、CE 分别延长至M 、N ，使DM ＝21BD ，EN ＝21CE ，得到图③，请解答下列问题： (1)若AB ＝AC ，请探究下列数量关系：①在图②中，BD 与CE 的数量关系是________________；②在图③中，猜想AM 与AN 的数量关系、∠MAN 与∠BAC 的数量关系，并证明你的猜想；(2)若AB ＝k·AC(k＞1)，按上述操作方法，得到图④，请继续探究：AM 与AN 的数量关系、∠MAN 与∠BAC 的数量关系，直接写出你的猜想，不必证明．7、如图，二次函数的图象经过点D(0，)，且顶点C的横坐标为4，该图象在x 轴上截得的线段AB 的长为6. ⑴求二次函数的解析式；⑵该抛物线的对称轴上找一点P ，使PA+PD 最小，求出点P 的坐标；⑶在抛物线上是否存在点Q ，使△QAB 与△ABC 相似？如果存在，求出点Q 的坐标；如果不存在，请说明理由．3978、如图，已知点A （0，1）是y 轴上一个定点，点B 是x 轴上一个动点，以AB 为边，在OAB ∠外部作,OAB BAE ∠=∠过点B 作,AB BC ⊥交AE 于点C ，设点C 的坐标为（y x ,），当点B 在x 轴上运动时，求y 关于x 的函数关系式。

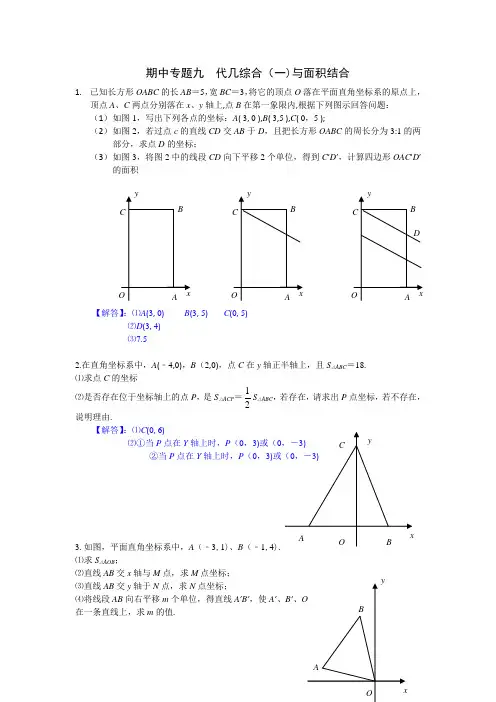
期中专题九 代几综合（一)与面积结合1. 已知长方形OABC 的长AB ＝5，宽BC ＝3，将它的顶点O 落在平面直角坐标系的原点上，顶点A 、C 两点分别落在x 、y 轴上,点B 在第一象限内,根据下列图示回答问题：（1） 如图1，写出下列各点的坐标：A ( 3, 0 ),B ( 3,5 ),C ( 0，5 );（2） 如图2，若过点c 的直线CD 交AB 于D ，且把长方形OABC 的周长分为3:1的两部分，求点D 的坐标；（3） 如图3，将图2中的线段CD 向下平移2个单位，得到C ’D ’，计算四边形OAC ’D ’的面积【解答】：⑴A (3, 0)B (3, 5)C (0, 5) ⑵D (3, 4)⑶7.52.在直角坐标系中，A (﹣4,0)，B （2,0)，点C 在y 轴正半轴上，且S △ABC ＝18. ⑴求点C 的坐标⑵是否存在位于坐标轴上的点P ，是S △ACP ＝12S △ABC ，若存在，请求出P 点坐标，若不存在，说明理由. 【解答】：⑴C (0, 6) ⑵①当P 点在Y 轴上时，P （0，3)或（0②当P 点在Y 轴上时，P （0，3)3.如图，平面直角坐标系中，A （﹣3,1)、B （﹣1,4⑴求S △AOB ；⑵直线AB 交x 轴与M 点，求M 点坐标；⑶直线AB 交y 轴于N 点，求N 点坐标；⑷将线段AB 向右平移m 个单位，得直线A ’B ’，使A ’在一条直线上，求m 的值.【解答】：⑴S△OAB＝3×4－12(3×2)－13(4×1)＝12－1.5－3－2＝5.5⑵设OM＝x S△BOM＝12x×4＝12x×1＋5.5＝>4x＝x＋11∴M(－113，0)⑶设ON＝y S△AON＝12×3＝12y×1＋5.5＝>3y＝y＋11y＝5.5∴M(5.5，0)⑷m＝113同第②问。

2015北京
点P的存在范围： 半径为2与半径为1之间的圆环 P’在⊙C内部 外实内虚
2015北京
点P既在线段AB上，又在圆环上
线段AB与圆环有交点
2015北京
怎么能又快又好地让学生理解圆环C是 如何运动，并观察相交情况呢？ 怎么求出点C的坐标呢？ 题目中说的是点C在x轴上运动，圆环的 移动如何体现呢？
2015北京
根据“曲定直动”
将圆环C固定下来， 让线段AB进行左右平移运动.
2015北京
我们可以观察出线段AB的临界位置
2015北京
既然是相对运动，无论怎么对线段AB进行平移，点A的横坐标永远为6.
线段A1B1与⊙C相切，发现点C位于点A1左侧4个单位，
此时点C横坐标为2；
线段A2B2与⊙C相交，发现点C位于点A2右侧2个单位，
方法1：以点N为研究重心
问：直线l究竟会扫过哪里呢？ 答：直线l过点N，点N在⊙O上，因此直线l和⊙O一定有交点.
因此临界情况就是直线l为⊙O切线.
方法1：以点N为研究重心
问：最后这道题怎么做？ 答：点M既在红色区域内，又符合坐标（m，3）
方法2：以点M为研究重心
M，N为“相关矩形”的对角线顶点，说明两个点地位一样； 问：点M在哪里？ 答：坐标为（m，3），点M在直线y=3上.
①理解问题阶段： 将问题转化成“充气膨胀，何时接触”问题； ②分析探究问题阶段： 2. 找规律；6. 画图（视觉表达）； 7.聪明地猜想或测试； ③解答问题阶段： 完成直线的联立； ④检验问题阶段： 怎么算又快又好？
①理解问题阶段： 一个动点→“找两个点看看规律”； ②分析探究问题阶段： 将“非常距离”与“点到直线的距离”联系，发现相关性； ③解答问题阶段： 找到最短距离；解直角三角形；完成直线的联立； ④检验问题阶段： 怎么算又快又好？（参数比例，待定系数法）（曲定直动）

代几综合问题—知识讲解（提高）【中考展望】代几综合题是初中数学中覆盖面最广、综合性最强的题型．近几年的中考压轴题多以代几综合题的形式出现．解代几综合题一般可分为“认真审题、理解题意；探求解题思路；正确解答”三个步骤,解代几综合题必须要有科学的分析问题的方法．数学思想是解代几综合题的灵魂，要善于挖掘代几综合题中所隐含的重要的转化思想、数形结合思想、分类讨论的思想、方程（不等式）的思想等，把实际问题转化为数学问题，建立数学模型，这是学习解代几综合题的关键．题型一般分为：（1）方程与几何综合的问题；（2）函数与几何综合的问题；（3）动态几何中的函数问题；（4）直角坐标系中的几何问题；（5）几何图形中的探究、归纳、猜想与证明问题.题型特点：一是以几何图形为载体，通过线段、角等图形寻找各元素之间的数量关系，建立代数方程或函数模型求解；二是把数量关系与几何图形建立联系，使之直观化、形象化，从函数关系中点与线的位置、方程根的情况得出图形中的几何关系.以形导数，由数思形，从而寻找出解题捷径. 解代几综合题要灵活运用数形结合的思想进行数与形之间的相互转化，关键是要从题目中寻找这两部分知识的结合点，从而发现解题的突破口.【方法点拨】方程与几何综合问题是中考试题中常见的中档题，主要以一元二次方程根的判别式、根与系数的关系为背景，结合代数式的恒等变形、解方程（组）、解不等式（组）、函数等知识．其基本形式有：求代数式的值、求参数的值或取值范围、与方程有关的代数式的证明．函数型综合题主要有：几何与函数结合型、坐标与几何、方程与函数结合型问题，是各地中考试题中的热点题型．主要是以函数为主线，建立函数的图象，结合函数的性质、方程等解题．解题时要注意函数的图象信息与方程的代数信息的相互转化．例如函数图象与x轴交点的横坐标即为相应方程的根；点在函数图象上即点的坐标满足函数的解析式等．函数是初中数学的重点，也是难点，更是中考命题的主要考查对象，由于这类题型能较好地考查学生的函数思想、数形结合思想、分类讨论思想、转化思想，能较全面地反映学生的综合能力，有较好的区分度，因此是各地中考的热点题型．几何综合题考查知识点多、条件隐晦，要求学生有较强的理解能力，分析能力，解决问题的能力，对数学知识、数学方法有较强的驾驭能力，并有较强的创新意识与创新能力．1．几何型综合题，常以相似形与圆的知识为考查重点，并贯穿其他几何、代数、三角等知识，以证明、计算等题型出现．2．几何计算是以几何推理为基础的几何量的计算，主要有线段和弧长的计算，角的计算，三角函数值的计算，以及各种图形面积的计算等．3．几何论证题主要考查学生综合应用所学几何知识的能力．4．解几何综合题应注意以下几点：（1）注意数形结合，多角度、全方位观察图形，挖掘隐含条件，寻找数量关系和相等关系；（2）注意推理和计算相结合，力求解题过程的规范化；（3）注意掌握常规的证题思路，常规的辅助线作法；（4）注意灵活地运用数学的思想和方法．【典型例题】类型一、方程与几何综合的问题1.（2015•大庆模拟）如图，Rt△ABC中，∠C=90°，BC=8cm，AC=6cm．点P从B出发沿BA向A运动，速度为每秒1cm，点E是点B以P为对称中心的对称点，点P运动的同时，点Q从A出发沿AC向C运动，速度为每秒2cm，当点Q到达顶点C时，P，Q同时停止运动，设P，Q两点运动时间为t秒．（1）当t为何值时，PQ∥BC？（2）设四边形PQCB的面积为y，求y关于t的函数关系式；（3）四边形PQCB面积能否是△ABC面积的？若能，求出此时t的值；若不能，请说明理由；（4）当t为何值时，△AEQ为等腰三角形？（直接写出结果）【思路点拨】（1）先在Rt△ABC中，由勾股定理求出AB=10，再由BP=t，AQ=2t，得出AP=10﹣t，然后由PQ∥BC，根据平行线分线段成比例定理，列出比例式，求解即可；（2）正确把四边形PQCB表示出来，即可得出y关于t的函数关系式；（3）根据四边形PQCB面积是△ABC面积的，列出方程，解方程即可；（4）△AEQ为等腰三角形时，分三种情况讨论：①AE=AQ；②EA=EQ；③QA=QE，每一种情况都可以列出关于t的方程，解方程即可．【答案与解析】解：（1）Rt△ABC中，∵∠C=90°，BC=8cm，AC=6cm，∴AB=10cm．∵BP=t，AQ=2t，∴AP=AB﹣BP=10﹣t．∵PQ∥BC，∴=，∴=，解得t=；（2）∵S四边形PQCB=S△ACB﹣S△APQ=AC•BC﹣AP•AQ•sinA∴y=×6×8﹣×（10﹣t）•2t•=24﹣t（10﹣t）=t2﹣8t+24，即y关于t的函数关系式为y=t2﹣8t+24；（3）四边形PQCB面积能是△ABC面积的，理由如下：由题意，得t2﹣8t+24=×24，整理，得t2﹣10t+12=0，解得t1=5﹣，t2=5+（不合题意舍去）．故四边形PQCB面积能是△ABC面积的，此时t的值为5﹣；（4）△AEQ为等腰三角形时，分三种情况讨论：①如果AE=AQ，那么10﹣2t=2t，解得t=；②如果EA=EQ，那么（10﹣2t）×=t，解得t=；③如果QA=QE，那么2t×=5﹣t，解得t=．故当t为秒秒秒时，△AEQ为等腰三角形．【总结升华】本题考查了勾股定理，等腰三角形的判定等，综合性较强，难度适中．解答此题时要注意分类讨论，不要漏解；其次运用方程思想是解题的关键．举一反三：【变式】（2016•镇江）如图1，在菱形ABCD中，AB=6，tan∠ABC=2，点E从点D出发，以每秒1个单位长度的速度沿着射线DA的方向匀速运动，设运动时间为t（秒），将线段CE绕点C顺时针旋转一个角α（α=∠BCD），得到对应线段CF．（1）求证：BE=DF；（2）当t= 秒时，DF的长度有最小值，最小值等于；（3）如图2，连接BD、EF、BD交EC、EF于点P、Q，当t为何值时，△EPQ是直角三角形？（4）如图3，将线段CD绕点C顺时针旋转一个角α（α=∠BCD），得到对应线段CG．在点E的运动过程中，当它的对应点F位于直线AD上方时，直接写出点F到直线AD的距离y 关于时间t的函数表达式．【答案】解：（1）∵∠ECF=∠BCD，即∠BCE+∠DCE=∠DCF+∠DCE，∴∠DCF=∠BCE，∵四边形ABCD是菱形，∴DC=BC，在△DCF和△BCE中，∵，∴△DCF≌△BCE（SAS），∴DF=BE；（2）如图1，当点E运动至点E′时，DF=BE′，此时DF最小，在Rt△ABE′中，AB=6，tan∠ABC=tan∠BAE′=2，∴设AE′=x，则BE′=2x，∴AB=x=6，则AE′=6∴DE′=6+6，DF=BE′=12，故答案为：6+6，12；（3）∵CE=CF，∴∠CEQ＜90°，①当∠EQP=90°时，如图2①，∵∠ECF=∠BCD，BC=DC，EC=FC，∴∠CBD=∠CEF，∵∠BPC=∠EPQ，∴∠BCP=∠EQP=90°，∵AB=CD=6，tan∠ABC=tan∠ADC=2，∴DE=6，∴t=6秒；②当∠EPQ=90°时，如图2②，∵菱形ABCD的对角线AC⊥BD，∴EC与AC重合，∴DE=6，∴t=6秒；（4）y=t﹣12﹣，如图3，连接GF分别交直线AD、BC于点M、N，过点F作FH⊥AD于点H，由（1）知∠1=∠2，又∵∠1+∠DCE=∠2+∠GCF，∴∠DCE=∠GCF，在△DCE和△GCF中，∵，∴△DCE≌△GCF（SAS），∴∠3=∠4，∵∠1=∠3，∠1=∠2，∴∠2=∠4，∴GF∥CD，又∵AH∥BN，∴四边形CDMN是平行四边形，∴MN=CD=6，∵∠BCD=∠DCG，∴∠CGN=∠DCN=∠CNG，∴CN=CG=CD=6，∵tan∠ABC=tan∠CGN=2，∴GN=12，∴GM=6+12，∵GF=DE=t，∴FM=t﹣6﹣12，∵tan∠FMH=tan∠ABC=2，∴FH=（t﹣6﹣12），即y=t﹣12﹣．类型二、函数与几何综合问题2.如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P．已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）．⑴求c、b（可以用含t的代数式表示）；⑵当t>1时，抛物线与线段AB交于点M．在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；⑶在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接．．写出t的取值范围．【思路点拨】（1）由抛物线y=x2+bx+c经过点O和点P，将点O与P的坐标代入方程即可求得c，b；（2）当x=1时，y=1-t，求得M的坐标，则可求得∠AMP的度数；（3）根据图形，可直接求得答案．【答案与解析】解：（1）把x=0，y=0代入y=x2+bx+c，得c=0，再把x=t，y=0代入y=x2+bx，得t2+bt=0，∵t＞0，∴b=-t；（2）不变．∵抛物线的解析式为：y=x2-tx，且M的横坐标为1，∴当x=1时，y=1-t，∴M（1，1-t），∴AM=|1-t|=t-1，∵OP=t ，∴AP=t-1， ∴AM=AP ，∵∠PAM=90°，∴∠AMP=45°；（3）72＜ｔ＜113．①左边4个好点在抛物线上方，右边4个好点在抛物线下方：无解； ②左边3个好点在抛物线上方，右边3个好点在抛物线下方： 则有-4＜y 2＜-3，-2＜y 3＜-1， 即-4＜4-2t ＜-3，-2＜9-3t ＜-1，∴72＜ｔ＜４且103＜ｔ＜113，解得72＜ｔ＜113；③左边2个好点在抛物线上方，右边2个好点在抛物线下方：无解； ④左边1个好点在抛物线上方，右边1个好点在抛物线下方：无解； ⑤左边0个好点在抛物线上方，右边0个好点在抛物线下方：无解； 综上所述，t 的取值范围是：72＜ｔ＜113．【总结升华】此题考查了二次函数与点的关系．此题综合性很强，难度适中，解题的关键是注意数形结合与方程思想的应用．类型三、动态几何中的函数问题3. 如图，在平面直角坐标系xOy 中，已知二次函数2+2y ax ax c =+的图象与y 轴交于(0,3)C ，与x 轴交于A 、B 两点，点B 的坐标为(-3,0)（1）求二次函数的解析式及顶点D 的坐标；（2）点M 是第二象限内抛物线上的一动点，若直线OM 把四边形ACDB 分成面积为1:2的两部分，求出此时点M 的坐标；（3）点P 是第二象限内抛物线上的一动点，问：点P 在何处时△CPB 的面积最大？最大面积是多少？并求出此时点P 的坐标.【思路点拨】（1）抛物线的解析式中只有两个待定系数，因此只需将点B 、C 的坐标代入其中求解即可．（2）先画出相关图示，连接OD 后发现：S △OBD ：S 四边形ACDB =2：3，因此直线OM 必须经过线段BD 才有可能符合题干的要求；设直线OM 与线段BD 的交点为E ，根据题干可知：△OBE 、多边形OEDCA 的面积比应该是1：2或2：1，即△OBE 的面积是四边形ACDB 面积的1233或，所以先求出四边形ABDC 的面积，进而得到△OBE 的面积后，可确定点E 的坐标，首先求出直线OE （即直线OM ）的解析式，联立抛物线的解析式后即可确定点M 的坐标（注意点M 的位置）．（3）此题必须先得到关于△CPB 面积的函数表达式，然后根据函数的性质来求出△CPB 的面积最大值以及对应的点P 坐标；通过图示可发现，△CPB 的面积可由四边形OCPB 的面积减去△OCB 的面积求得，首先设出点P 的坐标，四边形OCPB 的面积可由△OCP 、△OPB 的面积和得出． 【答案与解析】解：（1）由题意，得：3,9-60.c a a c =⎧⎨+=⎩ 解得：-1,3.a c =⎧⎨=⎩所以，二次函数的解析式为：2--23y x x =+ ，顶点D 的坐标为（-1，4）. （2）画图由Ａ、Ｂ、Ｃ、Ｄ四点的坐标，易求四边形ACDB 的面积为9.直线BD 的解析式为y=2x+6.设直线OM 与直线BD 交于点E ，则△OBE 的面积可以为3或6.①当1=9=33OBE S ∆⨯时，如图，易得E 点坐标（-2，-2），直线OE 的解析式为y=-x.E M xy O A BCD设M 点坐标（x ，-x ），21223113113,().22x x x x x -=--+---+==舍 ∴113113M ,22--+（） ② 当时，同理可得M 点坐标．∴ M 点坐标为（-1，4）．（3）如图，连接OP ，设P 点的坐标为(),m n ， ∵点P 在抛物线上，∴232n m m =-+-， ∴PB PO OPB OB S S S S =+-△C △C △△C111||222OC m OB n OC OB =⋅-+⋅-⋅ ()339332222m n n m =-+-=--()22333273.2228m m m ⎛⎫=-+=-++ ⎪⎝⎭∵3<0m -<，∴当32m =-时，154n =. △CPB 的面积有最大值27.8∴当点P 的坐标为315(,)24-时，△CPB 的面积有最大值，且最大值为27.8【总结升华】此题主要考查了二次函数解析式的确定、图形面积的解法以及二次函数的应用等知识；（2）问中，一定先要探究一下点M 的位置，以免出现漏解的情况．举一反三：【变式】如图所示，四边形OABC 是矩形，点A 、C 的坐标分别为（3，0），（0，1），点D 是线段BC 上的动点（与端点B 、C 不重合），过点D 作直线y ＝－12x ＋b 交折线OAB 于点E ．（1）记△ODE 的面积为S ，求S 与b 的函数关系式；（2）当点E 在线段OA 上时，若矩形OABC 关于直线DE 的对称图形为四边形OA 1B 1C 1，试探究OA 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由.yxDECOAB【答案】（1）由题意得B （3，1）．若直线经过点A （3，0）时，则b ＝32 若直线经过点B （3，1）时，则b ＝52若直线经过点C （0，1）时，则b ＝1.①若直线与折线OAB的交点在OA上时，即1＜b≤32，如图1，此时点E（2b，0）.∴S＝12OE·CO＝12×2b×1＝b.②若直线与折线OAB的交点在BA上时，即32＜b＜52，如图2，此时点E（3，32b-），D（2b－2，1）.∴S＝S矩－(S△OCD＋S△OAE＋S△DBE)＝ 3－[12(2b－1)×1＋12×(5－2b)•(52b-)＋12×3(32b-)]（2）如图3，设O1A1与CB相交于点M，C1B1与OA相交于点N，则矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积．由题意知，DM∥NE，DN∥ME，∴四边形DNEM 为平行四边形,根据轴对称知，∠MED＝∠NED, 又∠MDE＝∠NED，∴∠MED＝∠MDE，MD＝ME，∴平行四边形DNEM为菱形．过点D作DH⊥OA，垂足为H，设菱形DNEM的边长为a，由题可知，D（2b-2，1），E（2b，0），∴DH=1，HE=2b-（2b-2）=2，∴HN=HE-NE=2-a，则在Rt△DHM中，由勾股定理知：222(2)1a a=-+，∴a=5 . 4.∴S四边形DNEM ＝NE·DH＝54．∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化，面积始终为54．类型四、直角坐标系中的几何问题4. 如图所示，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA＝3，OC＝2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．（1）直接写出点E、F的坐标；（2）设顶点为F的抛物线交y轴正半轴．．．于点P，且以点E、F、P为顶点的三角形是等腰三角形，求该抛物线的解析式；（3）在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．【思路点拨】（1）由轴对称的性质，可知∠FBD=∠ABD，FB=AB，可得四边形ABFD是正方形，则可求点E、F的坐标；（2）已知抛物线的顶点，则可用顶点式设抛物线的解析式. 因为以点E、F 、P 为顶点的等腰三角形没有给明顶角的顶点，而顶角和底边都是唯一的，所以要抓住谁是顶角的顶点进行分类，可分别以E 、F 、P 为顶角顶点；（3）求周长的最小值需转化为利用轴对称的性质求解. 【答案与解析】解：(1)E(3,1)；F(1,2)；(2)连结EF ，在Rt △EBF 中,∠B=90°，∴EF=5212222=+=+BF EB .设点P 的坐标为(0,n),n ＞0,∵顶点F(1,2), ∴设抛物线的解析式为y=a(x-1)2+2，(a ≠0)．①如图1，当EF=PF 时，EF 2=PF 2，∴12+(n-2)2=5，解得n 1=0(舍去)，n 2=4. ∴P(0，4)，∴4=a(0-1)2+2，解得a=2， ∴抛物线的解析式为y=2(x-1)2+2．②如图2，当EP=FP 时，EP 2=FP 2，∴(2-n)2+1=(1-n)2+9，解得n=－25(舍去)③当EF=EP 时，EP=5＜3，这种情况不存在. 综上所述，符合条件的抛物线为y=2(x-1)2+2．(3)存在点M 、N ，使得四边形MNFE 的周长最小．如图3，作点E 关于x 轴的对称点E′，作点F 关于y 轴的对称点F′，连结E′F′，分别与x 轴、y 轴交于点M 、N ，则点M 、N 就是所求. 连结NF 、ME. ∴E′(3，-1)、F′(-1，2)，NF=NF′，ME=ME′. ∴BF′=4，BE′=3. ∴FN+NM+ME=F′N+NM+ME′=F′E′=2243 =5. 又∵EF=5，∴FN+MN+ME+EF=5+5， 此时四边形MNFE 的周长最小值为5+5.【总结升华】本题考查了平面直角坐标系、等腰直角三角形、抛物线解析式的求法、利用轴对称求最短距离以及数形结合、分类讨论等数学思想. 分类讨论的思想要依据一定的标准，对问题分类、求解，要特别注意分类原则是不重不漏，最简分类常见的依据是：一是依据概念分类，如判断直角三角形时明确哪个角可以是直角，两个三角形相似时分清哪两条边是对应边；二是依运动变化的图形中的分界点进行分类，如一个图形在运动过程中，与另一个图形重合部分可以是三角形，也可以是四边形、五边形等. 几何与函数的综合题是中考常见的压轴题型，解决这类问题主要分为两步：一是利用线段的长确定出几何图形中各点的坐标；二是用待定系数法求函数关系式．类型五、几何图形中的探究、归纳、猜想与证明问题5. 如图所示，以等腰三角形AOB 的斜边为直角边向外作第2个等腰直角三角形ABA 1，再以等腰直角三角形ABA 1的斜边为直角边向外作第3个等腰直角三角形A 1BB 1，……，如此作下去，若OA=OB=1，则第n 个等腰直角三角形的面积Ｓ＝ ________（n 为正整数）．B 2B 1A 1BOA【思路点拨】本题要先根据已知的条件求出S 1、S 2的值，然后通过这两个面积的求解过程得出一般性的规律，进而可得出S n 的表达式．【总结升华】本题要先从简单的例子入手得出一般化的结论，然后根据得出的规律去求特定的值． 举一反三：【变式】阅读下面的文字，回答后面的问题．求3+32+33+…+3100的值． 解：令S=3+32+33+…+3100（1），将等式两边提示乘以3得到：3S=32+33+34+…+3101（2）， （2）-（1）得到：2S=3101-3问题：（1）2+22+…+22011的值为__________________；（直接写出结果）（2）求4+12+36+…+4×350的值；（3）如图，在等腰Rt△OAB中，OA=AB=1，以斜边OB为腰作第二个等腰Rt△OBC，再以斜边OC为腰作第三个等腰Rt△OCD，如此下去…一直作图到第8个图形为止．求所有的等腰直角三角形的所有斜边之和．（直接写出结果）．【答案】解：（1）22012-2．（2）令S=4+12+36+…+4×350 ①，将等式两边提示乘以3得到：3S=12+36+108+…+4×351②，②-①得到：2S=4×341-4∴S=2×351-2∴4+12+36+…+4×350=2×351-2．（3）92-2 2-1（）．。

代数与几何综合题代数与几何综合题从内容上来说，是把代数中的数与式、方程与不等式、函数，几何中的三角形、四边形、圆等图形的性质，以及解直角三角形的方法、图形的变换、相似等内容有机地结合在一起，同时也融入了开放性、探究性等问题，如探究条件、探究结论、探究存在性等。

经常考察的题目类型主要有坐标系中的几何问题（简称坐标几何问题），以及图形运动过程中求函数解析式问题等。

解决代数与几何综合题，第一，需要认真审题，分析、挖掘题目的隐含条件，翻译并转化为显性条件；第二，要善于将复杂问题分解为基本问题，逐个击破；第三，要善于联想和转化，将以上得到的显性条件进行恰当地组合，进一步得到新的结论，尤其要注意的是，恰当地使用分析综合法及方程与函数的思想、转化思想、数行结合思想、分类与整合思想等数学思想方法，能更有效地解决问题。

第一类：与反比例函数相关1．（09北京）如图，点C 为⊙O 直径AB 上一点，过点C 的直线交⊙O 于点D 、E 两点，且∠ACD=45°，DF AB ⊥于点F ，EG AB ⊥ 于点G ． 当点C 在AB 上运动时，设AF x =，DE y =，下列 图象中，能表示y 与x 的函数关系的图象大致是（ ）2．如图，在平面直角坐标系中 ,二次函数)0(22≠+=a am ax y 的图象经过正方形ABOC 的三个顶点 A 、B 、C ，则m 的值为 ．3．（09延庆）阅读理解：对于任意正实数a b ，，20Q ≥，0a b ∴-≥，a b ∴+≥，只有当a b =时，等号成立．结论：在a b +≥a b ，均为正实数）中，若ab 为定值p，则a b +≥，A B C D只有当a b =时，a b +有最小值． 根据上述内容，回答下列问题： （1） 若0m >，只有当m = 时，1m m+有最小值 ． （2） 探索应用：已知(30)A -，，(04)B -，，点P 为双曲线12(0)y x x=>上的任意一点，过点P 作PC x ⊥轴于点C ，轴于y PD ⊥D ． 求四边形ABCD 面积的最小值，并说明此时 四边形ABCD 的形状．4．（08南通）已知双曲线k y x =与直线14y x =相交于A 、B 两点．第一象限上的点M （m ，n ）（在A 点左侧）是双曲线ky x=上的动点．过点B 作BD ∥y 轴交x 轴于点D ．过N （0，－n ）作NC ∥x 轴交双曲线k y x=于点E ，交BD 于点C ． （1）若点D 坐标是（－8，0），求A 、B 两点坐标及k 的值． （2）若B 是CD 的中点，四边形OBCE 的面积为4，求直线CM 的解析式．（3）设直线AM 、BM 分别与y 轴相交于P 、Q 两点，且MA =pMP ，MB =qMQ ，求p －q 的值．5．（西城）已知：反比例函数2y x =和8y x= 在平面直角坐标系xOy 第一象限中的图象如图所示，点A 在8y x =的图象上，AB ∥y 轴，与2y x=的图象交于点B ，AC 、BD 与x 轴平行，分别与2y x =、8y x=的图象交于点C 、D . （1）若点A 的横坐标为2，求梯形ACBD 的对角线的交点F 的坐标；（2）若点A 的横坐标为m ，比较△OBC 与△ABC 的面积的大小；（3）若△ABC 与以A 、B 、D 为顶点的三角形相似，请直接写出点A 的坐标.（第3题）（第4题）答案：（1） 点F 的坐标为17(2,)5.（2）OBC ABC S S ∆∆>. （3）点A 的坐标为(2,4)6．（07上海）如图，在直角坐标平面内，函数my x=（0x >，m 是常数）的图象经过(14)A ，，()B a b ，，其中1a >．过点A 作x 轴垂线，垂足为C ，过点B 作y 轴垂线，垂足为D ，连结AD ，DC ，CB ．（1）若ABD △的面积为4，求点B 的坐标； （2）求证：DC AB ∥；（3）当AD BC =时，求直线AB 的函数解析式． 答案：（1）点B 的坐标为 433⎛⎫ ⎪⎝⎭，； （2）DC AB ∴∥． （3）所求直线AB 的函数解析式是26y x =-+或5y x =-+二、与三角形相关7．（07北京）在平面直角坐标系xOy 中, 抛物线 y = mx 2+ 23mx + n 经过P (3, 5),A (0, 2)两点. (1) 求此抛物线的解析式;(2) 设抛物线的顶点为B , 将直线AB 沿y 轴向下平移两个单位得到直线l , 直线l 与抛物线的对称轴交于C 点, 求直线l 的解析式;(3) 在(2)的条件下, 求到直线OB , OC , BC 距离相等的点的坐标． 答案：(1)抛物线的解析式为: y =x x 332312++ 2(2)直线 l 的解析式为 y =33x (3) 到直线OB 、OC 、BC 距离相等的点的坐标分别为: M 1(332, 0)、 M 2 (0, 2)、 M 3(0, 2)、M 4 (23, 0).8． (08北京)平面直角坐标系xOy 中，抛物线y = x 2+ bx + c 与x 轴交于A , B 两点(点xCO D BA yA 在点B 的左侧), 与y 轴交于点C , 点B 的坐标为(3, 0), 将直线 y = kx 沿y 轴向上平移3个单位长度后恰好经过B , C 两点. (1) 求直线BC 及抛物线的解析式;(2) 设抛物线的顶点为D , 点P 在抛物线的对称轴上, 且APD =ACB , 求点P 的坐标; (3) 连结CD , 求OCA 与OCD 两角和的度数.答案：(1) 直线BC 的解析式为 y = x + 3. 抛物线的解析式为 y = x 24x + 3.(2)点P 的坐标为 (2, 2) 或 (2, 2). (3) OCA 与OCD 两角和的度数为45. 9．（密云） 已知：如图，抛物线222(0)y x mx m m =-++>与x轴交于A 、B 两点，点A 在点B 的左边，C 是抛物线 上一动点（点C 与点A 、B 不重合），D 是OC 中点，连结BD 并延长，交AC 于点E ． （1）求A 、B 两点的坐标（用含m 的代数式表示）； （2）求CEAE的值； （3）当C 、A 两点到y 轴的距离相等，且85CED S =V 时， 求抛物线和直线BE 的解析式．答案：（1）A （m -，0），B （2m ，0）． （2）23CE AE =． （3）抛物线的解析式为 228y x x =-++．直线BE 的解析式为 41633y x =-+ 10．（崇文09）如图，抛物线两点轴交于与B A x bx ax y ,32-+=，与y 轴交于点C ，且OA OC OB 3==．（I ）求抛物线的解析式；（II ）探究坐标轴上是否存在点P ，使得以点C A P ,,为顶点的三角形为直角三角形若存在，求出P 点理由；（III ）直线131+-=x y 交y 轴于D 点，E 为抛物线顶点．若α=∠DBC ，βαβ-=∠求,CBE 的答案： （I ）322--=∴x x y（II ）)31,0(1P )0,9(2P ，)0,0(3P（III ）︒=∠=∠-∠=∠-∠45OBC DBO αβα．11. 东城) 如图，已知在平面直角坐标系xOy 中，直角梯形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA ＝AB ＝2，OC ＝3，过点B 作BD ⊥BC ，交OA 于点D ．将∠DBC 绕点B 按顺时针方向旋转，角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F ．（1）求经过A 、B 、C 三点的抛物线的解析式；（2）当BE 经过（1）中抛物线的顶点时，求CF 的长；（3）在抛物线的对称轴上取两点P 、Q （点Q 在点P 的上方），且PQ ＝1，要使四边形BCPQ 的周长最小，求出P 、Q 两点的坐标．答案：（1）224233y x x =-++． （2）由224233y x x =-++＝228(1)33x --+． CF ＝FM ＋CM＝73． （3）点P 的坐标为（1，23）三、与面积有相关12．（通县）已知如图，ABC ∆中，AC BC =，BC 与x 轴平行，点A 在x 轴上，点C 在y 轴上，抛物线254y ax ax =-+经过ABC ∆的三个顶点，（1）求出该抛物线的解析式；（2）若直线7+=kx y 将四边形ACBD 面积平分，求此直线的解析式.（3）若直线b kx y +=将四边形ACBD 的周长和面积同时分成相等的两部分，请你确定b kx y +=中k 的取值范围.13．（顺义）已知，如图，抛物线24(0)y ax bx a =++≠与y 轴交于点C ，与x 轴交于点A B ，，点A 的坐标为(40)-，，对称轴是1x =-． （1）求该抛物线的解析式；（2）点M 是线段AB 上的动点，过点M 作MN ∥AC ，分别交y 轴、BC 于点P 、N ，连接CM ．当CMN △的面积最大时，求点M 的坐标；（3）在（2）的条件下，求CPNABCS S ∆∆的值. 四、与最值相关14．（09石景山）平面直角坐标系中有一张矩形纸片OABC ，O 为坐标原点，A 点坐标为（10，0），C 点坐标为（0，6），D 是BC 边上的动点（与点B 、C 不重合）．如图②,将△COD 沿OD 翻折，得到△FOD ；再在AB 边上选取适当的点E ，将△BDE 沿DE 翻折，得到△GDE ，并使直线DG ，DF 重合．（1）图①中，若△COD 翻折后点F 落在OA 边上，求直线DE 的解析式．（2）设（1）中所求直线DE 与x 轴交于点M ，请你猜想过点M 、C 且关于y 轴对称的抛物线与直线DE 的公共点的个数，在图①的图形中，通过计算验证你的猜想． （3）图②中，设E （10，b ），求b 的最小值．答案：（1）直线DE 的解析式：y =-x +12（2）直线DE :y =-x +12与抛物线:21624y x =-+只有一个公共点 （3）b 2111(5)66m =-+ 115,6m b ∴==最小值当15．已知抛物线22y ax bx =++的图像经过点A 和点B ．（1）求该抛物线的解析式；(2) 把(1)中的抛物线先向左平移1个单位，再向上或向下平移多少个单位能使抛物线与直线AB 只有一个交点 求出此时抛物线的解析式；（3）将（2）中的抛物线向右平移52个单位，再向下平移t 个单位（t >0），此时，抛物线与x 轴交于M 、N 两点，直线AB 与y 轴交于点P ，当t 为何值时，过M 、N 、P 三点的圆的面积最小最小面积是多少答案：（1）抛物线的解析式为232y x x =-+.(2) 析式为21()2y x =-（３）当5t =时，过M 、N 、P 三点的圆的面积最小，最小面积为9π图① 图②16．（09海淀）如图13，在平面直角坐标系xOy 中，直线233+-=x y 分别交x 轴、y 轴于C 、A 两点.将射线AM 绕着点A 顺时针旋转45°得到射线AN .点D 为AM 上的动点，点B 为AN 上的动点，点C 在∠MAN 的内部.（1） 求线段AC 的长；（2） 当AM ∥x 轴，且四边形ABCD 为梯形时，求△BCD 的面积； （3） 求△BCD 周长的最小值；（4） 当△BCD 的周长取得最小值，且BD =3时,△BCD 的面积为 . 答案：（1） AC =4.（2）当AM ∥x 轴，且四边形ABCD 为梯形时，S △BCD = 23-2. （3）∴△BCD 的周长的最小值为42. （4）43.五、与四边形及圆相关 17．年西城)已知：在如图1所示的平面直角坐标系xOy 中，A ，C 两点的坐标分别为(2,3)A ，(,3)C n -（其中n ＞0），点B 在x 轴的正半轴上．动点P 从点O 出发，在四边形OABC 的边上依次沿O —A —B —C 的顺序向点C 移动，当点P 与点C 重合时停止运动．设点P 移动的路径的长为l ，△POC 的面积为S ，S 与l 的函数关系的图象如图2所示，其中四边形ODEF 是等腰梯形．（1）结合以上信息及图2填空：图2中的m = ； （2）求B ，C 两点的坐标及图2中OF 的长；（3）在图1中，当动点P 恰为经过O ，B 两点的抛物线W 的顶点时， ① 求此抛物线W 的解析式；② 若点Q 在直线1y =-上方的抛物线W 上，坐标平面内另有一点R ，满足以B ，P ，Q ，R 四点为顶点的四边形是菱形，求点Q 的坐标．x答案：（1）中的m（2）2D OF x DE=+=（3）符合题意的点Q 的坐标是1(0,0)Q ，219)Q ．18.（12.年1石景山）如图，矩形'''O BC A 是矩形ABCO 绕点B 顺时针旋转得到的．其中点C O ,'在x 轴负半轴上，线段OA 在y 轴正半轴上，B 点的坐标为()3,1-．（1）如果二次函数()02≠++=a c bx ax y 的图象经过'O O 、两点且图象顶点M 的纵坐标为1-．求这个二次函数的解析式； （2）求边''A O 所在直线的解析式；（3）在（1）中求出的二次函数图象上是否存在点P ，使得D CO MPO S S ''3∆∆=,若存在，请求出点P 的坐标，若不存在，请说明理由．答案：（1）x x y 22+= （2）3834+=x y （3）⎪⎪⎭⎫ ⎝⎛-+-217721731，P ， ⎪⎪⎭⎫ ⎝⎛+-2177217-32，P ．19．（怀柔）如图，在平面直角坐标系中，顶点为（4，1-）的抛物线交y 轴于A 点，交x 轴于B ，C 两点（点B 在点C 的左侧）. 已知A 点坐标为（0，3）.（1）求此抛物线的解析式；（2）过点B 作线段AB 的垂线交抛物线于点D ， 如果以点C 为圆心的圆与直线BD 相切，请判断抛物线的对称轴l 与⊙C 有怎样的位置关系，并给出证明；（3）已知点P 是抛物线上的一个动点，且位于A ，C 两点之间，问：当点P 运动到什么位置时，PAC ∆的面积最大并求出此时P 点的坐标和PAC ∆的最大面积.答案：（1）抛物线为2211(4)1244y x x x =--=-+ (2) 答：l 与⊙C 相交. （3）PAC ∆的面积最大为274.此时，P 点的坐标为（3，34-）. 20．（朝阳）在△ABC 中，D 为AB 边上一点，过点D 作DE∥BC 交AC 于点E ，以DE 为折线，将△ADE 翻折，设所得的△A’DE 与梯形DBCE 重叠部分的面积为y. (1)如图(甲)，若∠C=90°，AB=10，BC=6，31=AB AD ，则y 的值为 ； (2)如图(乙)，若AB=AC=10，BC=12，D 为AB 中点，则y 的值为 ； (3)若∠B=30°，AB=10，BC=12，设AD=x. ①求y 与x 的函数解析式；②y 是否有最大值，若有，求出y 的最大值；若没有，请说明理由.图(甲) 图(乙) 备用图答案：（1）38. （2）12. （3） ''DA E MA N y S S ∆∆=-292010103x ⎛⎫=--+ ⎪⎝⎭．当203x =时，y 值最大，最大值是10．。

中考总复习：代几综合问题【中考展望】代几综合题是初中数学中覆盖面最广、综合性最强的题型．近几年的中考压轴题多以代几综合题的形式出现．解代几综合题一般可分为“认真审题、理解题意；探求解题思路；正确解答”三个步骤,解代几综合题必须要有科学的分析问题的方法．数学思想是解代几综合题的灵魂，要善于挖掘代几综合题中所隐含的重要的转化思想、数形结合思想、分类讨论的思想、方程（不等式）的思想等，把实际问题转化为数学问题，建立数学模型，这是学习解代几综合题的关键．题型一般分为：（1）方程与几何综合的问题；（2）函数与几何综合的问题；（3）动态几何中的函数问题；（4）直角坐标系中的几何问题；（5）几何图形中的探究、归纳、猜想与证明问题.题型特点：一是以几何图形为载体，通过线段、角等图形寻找各元素之间的数量关系，建立代数方程或函数模型求解；二是把数量关系与几何图形建立联系，使之直观化、形象化．以形导数，由数思形，从而寻找出解题捷径. 解代几综合题要灵活运用数形结合的思想进行数与形之间的相互转化，关键是要从题目中寻找这两部分知识的结合点，从而发现解题的突破口.【方法点拨】方程与几何综合问题是中考试题中常见的中档题，主要以一元二次方程根的判别式、根与系数的关系为背景，结合代数式的恒等变形、解方程（组）、解不等式（组）、函数等知识．其基本形式有：求代数式的值、求参数的值或取值范围、与方程有关的代数式的证明．函数型综合题主要有：几何与函数结合型、坐标与几何、方程与函数结合型问题，是各地中考试题中的热点题型．主要是以函数为主线，建立函数的图象，结合函数的性质、方程等解题．解题时要注意函数的图象信息与方程的代数信息的相互转化．例如函数图象与x轴交点的横坐标即为相应方程的根；点在函数图象上即点的坐标满足函数的解析式等．函数是初中数学的重点，也是难点，更是中考命题的主要考查对象，由于这类题型能较好地考查学生的函数思想、数形结合思想、分类讨论思想、转化思想，能较全面地反映学生的综合能力，有较好的区分度，因此是各地中考的热点题型．几何综合题考查知识点多、条件隐晦，要求学生有较强的理解能力，分析能力，解决问题的能力，对数学知识、数学方法有较强的驾驭能力，并有较强的创新意识与创新能力．1．几何型综合题，常以相似形与圆的知识为考查重点，并贯穿其他几何、代数、三角等知识，以证明、计算等题型出现．2．几何计算是以几何推理为基础的几何量的计算，主要有线段和弧长的计算，角的计算，三角函数值的计算，以及各种图形面积的计算等．3．几何论证题主要考查学生综合应用所学几何知识的能力．4．解几何综合题应注意以下几点：（1）注意数形结合，多角度、全方位观察图形，挖掘隐含条件，寻找数量关系和相等关系；（2）注意推理和计算相结合，力求解题过程的规范化；（3）注意掌握常规的证题思路，常规的辅助线作法；（4）注意灵活地运用数学的思想和方法．【典型例题】类型一、方程与几何综合的问题1．如图所示，在梯形ABCD中，AD∥BC（BC＞AD），∠D＝90°，BC＝CD＝12，∠ABE＝45°，若AE ＝10，则CE的长为_________.【思路点拨】过B作DA的垂线交DA的延长线于M，M为垂足，延长DM到G，使MG=CE，连接BG．求证△BEC≌△BGM，△ABE≌△ABG，设CE=x，在直角△ADE中，根据AE2=AD2+DE2求x的值，即CE的长度．【答案与解析】解：过B作DA的垂线交DA的延长线于M，M为垂足，延长DM到G，使MG=CE，连接BG，∴∠AMB=90°，∵AD∥CB，∠DCB=90°，∴∠D=90°，∴∠AMB=∠DCB=∠D=90°，∴四边形BCDM为矩形．∵BC=CD，∴四边形BCDM是正方形，∴BC=BM，且∠ECB=∠GMB，MG=CE，∴Rt△BEC≌Rt△BGM．∴BG=BE，∠CBE=∠GBM，∵∠CBE+∠EBA+∠ABM=90°，且∠ABE=45°∴∠CBE+∠ABM=45°∴∠ABM+∠GBM=45°∴∠ABE=∠ABG=45°，∴△ABE≌△ABG，AG=AE=10．设CE=x，则AM=10-x，AD=12-（10-x）=2+x，DE=12-x，在Rt△ADE中，AE2=AD2+DE2，∴100=（x+2）2+（12-x）2，即x2-10x+24=0；解得：x1=4，x2=6．故CE的长为4或6．【总结升华】本题考查了直角三角形中勾股定理的运用，考查了全等三角形的判定和性质，本题中求证△ABE≌△ABG，从而说明AG=AE=10是解题的关键．类型二、函数与几何问题2．如图，二次函数y =（x-2）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A（1，0）及点B．（1）求二次函数与一次函数的解析式；（2）根据图象，写出满足kx+b≥（x-2）2+m的x的取值范围．【思路点拨】（1）将点A（1，0）代入y=（x-2）2+m求出m的值，根据点的对称性，将y=3代入二次函数解析式求出B的横坐标，再根据待定系数法求出一次函数解析式；（2）根据图象和A、B的交点坐标可直接求出满足kx+b≥（x-2）2+m的x的取值范围．【答案与解析】解：（1）将点A（1，0）代入y=（x-2）2+m得，（1-2）2+m=0，1+m=0，m=－1，则二次函数解析式为y=（x-2）2-1． 当x=0时，y=4-1=3， 故C 点坐标为（0，3），由于C 和B 关于对称轴对称，在设B 点坐标为（x ，3）， 令y=3，有（x-2）2-1=3，解得 x=4或x=0．则B 点坐标为（4，3）．设一次函数解析式为y=kx+b ，将A （1，0）、B （4，3）代入y=kx+b 中，得，解得，则一次函数解析式为y=x-1； （2）∵A 、B 坐标为（1，0），（4，3），∴当kx+b≥（x-2）2+m 时，1≤x≤4．【总结升华】本题考察了待定系数法求二次函数,一次函数函数解析式以及数形结合法解不等式.求出B 点坐标是解题的关键．举一反三：【变式】如图，二次函数的图象与x 轴交于A 、B 两点，其中A 点坐标为（－1，0），点C （0，5）、D （1，8）在抛物线上，M 为抛物线的顶点． （1）求抛物线的解析式． （2）求△MCB 的面积．2(0)y ax bx c a =++≠【答案】解：(1)设抛物线的解析式为，根据题意，得， 解之，得． ∴所求抛物线的解析式为．（2）∵C 点的坐标为（0，5）．∴OC ＝5．令，则，解得．∴B 点坐标为（5，0）．∴OB ＝5．∵，∴顶点M 坐标为（2，9）．过点M 作MN ⊥AB 于点N ，则ON ＝2，MN ＝9．∴. 类型三、动态几何中的函数问题2y ax bx c =++058a b c c a b c -+=⎧⎪=⎨⎪++=⎩145a b c =-⎧⎪=⎨⎪=⎩245y x x =-++0y =2450x x -++=121,5x x =-=2245(2)9y xx x =-++=--+11(59)9(52)551522MCB BNM OBC OCMN S S S S ∆∆∆=+-=+⨯⨯--⨯⨯=梯形3．如图，在平面直角坐标系中，已知点A（-2，-4），OB=2，抛物线y=ax2+bx+c经过点A、O、B 三点．（1）求抛物线的函数表达式；（2）若点M是抛物线对称轴上一点，试求AM+OM的最小值；（3）在此抛物线上，是否存在点P，使得以点P与点O、A、B为顶点的四边形是梯形？若存在，求点P的坐标；若不存在，请说明理由．【思路点拨】（1）把A、B、O的坐标代入到y=ax2+bx+c得到方程组，求出方程组的解即可；（2）根据对称求出点O关于对称轴的对称点B，连接AB,根据勾股定理求出AB的长，就可得到AM+OM 的最小值.（3）①若OB∥AP，根据点A与点P关于直线x=1对称，由A（-2，-4），得出P的坐标；②若OA∥BP，设直线OA的表达式为y=kx，设直线BP的表达式为y=2x+m，由B（2，0）求出直线BP的表达式为y=2x-4，得到方程组，求出方程组的解即可；③若AB∥OP，设直线AB的表达式为y=kx+m，求出直线AB，得到方程组求出方程组的解即可.【答案与解析】解：（1）由OB=2，可知B（2，0），将A（-2，-4），B（2，0），O（0，0）三点坐标代入抛物线y=ax2+bx+c，得（3）①如图1，若OB∥AP，此时点A与点P关于直线x=1对称，由A（-2，-4），得P（4，-4），则得梯形OAPB．②如图2，若OA∥BP，③如图3，若AB ∥OP ，设直线AB 的表达式为y=kx+m ，则解得综上所述，存在两点P （4，-4）或P （-4，-12）,使得以点P 与点O 、A 、B 为顶点的四边形是梯形．【总结升华】本题主要考查对梯形，解二元二次方程组，解一元二次方程，二次函数的性质，用待定系数法求一次函数的解析式等知识点的理解和掌握，综合运用性质进行计算是解此题的关键．举一反三：4202k m k m -=-+⎧⎨=+⎩，．12k m =⎧⎨=-⎩，．【变式】如图，直线与x 轴、y 轴的交点分别为B 、C ，点A 的坐标是（-2，0）． （1）试说明△ABC 是等腰三角形；（2）动点M 从A 出发沿x 轴向点B 运动，同时动点N 从点B 出发沿线段BC 向点C 运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M 运动t 秒时，△MON 的面积为S ．① 求S 与t 的函数关系式；② 设点M 在线段OB 上运动时，是否存在S ＝4的情形？若存在，求出对应的t 值；若不存在，请说明理由；③在运动过程中，当△MON 为直角三角形时，求t 的值．【答案】434+-=x y分为三种情况：I、当∠NOM=90°时，N在y轴上，即此时t=5；II 、当∠NMO=90°时，M 、N 的横坐标相等，即t-2=3-0.6t ，解得：t=3.125， III 、∠MNO 不可能是90°，即在运动过程中，当△MON 为直角三角形时，t 的值是5秒或3.125秒． 类型四、直角坐标系中的几何问题4．已知，如图所示，在平面直角坐标系中，四边形ABC0为梯形，BC ∥A0，四个顶点坐标分别为A （4，0），B （1，4），C （0，4），O （0，O ）．一动点P 从O 出发以每秒1个单位长度的速度沿OA 的方向向A 运动；同时，动点Q 从A 出发，以每秒2个单位长度的速度沿A→B→C 的方向向C 运动．两个动点若其中一个到达终点，另一个也随之停止．设其运动时间为t 秒． （1）求过A ，B ，C 三点的抛物线的解析式； （2）当t 为何值时，PB 与AQ 互相平分；（3）连接PQ ，设△PAQ 的面积为S ，探索S 与t 的函数关系式．求t 为何值时，S 有最大值？最大值是多少？【思路点拨】（1）设出抛物线的解析式，运用待定系数法可以直接求出抛物线的解析式．（2）根据PB 与AQ 互相平分可以得出四边形BQPA 是平行四边形，得出QB=PA 建立等量关系可以求出t 值．（3）是一道分段函数，分为Q 点在AB 上和在BC 上讨论，根据三角形的面积公式表示出S 与t 的关系式，就可以求出答案. 【答案与解析】解：（1）设抛物线的解析式为y=ax 2+bx+c （a≠0），代入A 、B 、C 三点的坐标，得16a 4044b c a b c c ++=⎧⎪++=⎨⎪=⎩1(4).2PAQQ p Sy x =-82sin ,5Q p y t t x θ==2184(4)(4255PAQSt t t t =-=-1614(4)82t -=【总结升华】本题是一道二次函数综合题.考察了二次函数的最值，待定系数法求二次函数解析式以及三角形面积的求解等.类型五、几何图形中的探究、归纳、猜想与证明问题5．一个质点在第一象限及轴、轴上运动，在第一秒钟，它从原点运动到，然后接着按图中箭头所示方向运动,即，且每秒移动一个单位，那么第35秒时质点所在位置的坐标是_______.【思路点拨】由题目中所给的质点运动的特点找出规律，到（2，0）用4秒，到（2，2）用6秒，到（0，2）用8秒，到（0，3）用9秒，到（3，3）用12秒，即可得出第35秒时质点所在位置的坐标． 【答案与解析】解：质点运动的速度是每秒运动一个单位长度，（0，0）→（0，1）→（1，1）→（1，0）用的秒数分别是1秒，2秒，3秒，到（2，0）用4秒，到（2，2）用6秒，到（0，2）用8秒，到（0，3）用9秒，到（3，3）用12秒，到（4，0）用16秒，依此类推，到（5，0）用35秒．故第35秒时质点所在位置的坐标是（5，0）． 【总结升华】此题主要考查了数字变化规律，解决本题的关键是正确读懂题意，能够正确确定点运动的顺序，确定运动的距离，从而可以得到到达每个点所用的时间. 举一反三：x y (01)，(00)(01)(11)(10)→→→→，，，， 012 3 xy1 2 3 …【变式】如图，一粒子在区域{（x，y）|x≥0，y≥0}内运动，在第1秒内它从原点运动到点B1（0，1），接着由点B1→C1→A1，然后按图中箭头所示方向在x轴，y轴及其平行线上运动，且每秒移动1个单位长度，求该粒子从原点运动到点P（16，44）时所需要的时间．【答案】解：设粒子从原点到达A n、B n、C n时所用的时间分别为a n、b n、c n，则有：a1=3，a2=a1+1，a3=a1+12=a1+3×4，a4=a3+1，a5=a3+20=a3+5×4，a6=a5+1，a2n-1=a2n-3+（2n-1）×4，a2n=a2n-1+1，∴a2n-1=a1+4[3+5+…+（2n-1）]=4n2-1，a2n=a2n-1+1=4n2，∴b2n-1=a2n-1-2（2n-1）=4n2-4n+1，b2n=a2n+2×2n=4n2+4n，c2n-1=b2n-1+（2n-1）=4n2-2n，c2n=a2n+2n=4n2+2n=（2n）2+2n，∴c n=n2+n，∴粒子到达（16，44）所需时间是到达点c44时所用的时间，再加上44-16=28（s），所以t=442+447+28=2008（s）．中考冲刺：代几综合问题—巩固训练（基础）【巩固练习】一、选择题1.如图，点G 、D 、C 在直线a 上，点E 、F 、A 、B 在直线b 上，若从如图所示的位置出发，沿直线b 向右匀速运动，直到EG 与BC 重合．运动过程中与矩形重合部分．．．．的面积（S ）随时间（t ）变化的图象大致是（ ）2.如图，在半径为1的⊙O 中，直径AB 把⊙O 分成上、下两个半圆，点C 是上半圆上一个动点（C 与点A 、B 不重合），过点C 作弦CD ⊥AB ，垂足为E ，∠OCD 的平分线交⊙O 于点P ，设CE=x ，AP=y ，下列图象中，最能刻画y 与x 的函数关系的图象是（ ）二、填空题3. 将抛物线y 1＝2x 2向右平移2个单位，得到抛物线ｙ２的图象如图所示，P 是抛物线y 2对称轴上的一个动点，直线x ＝t 平行于y 轴，分别与直线y ＝x 、抛物线y 2交于点A 、B ．若△ABP 是以点A 或点B 为直角顶点的等腰直角三角形，求满足的条件的t 的值，则t ＝ ．a b Rt GEF ∥，△GEF △ABCD三、解答题5.一个形如六边形的点阵.它的中心是一个点（算第一层）、第二层每边有两个点，第三层每边有三个点……依次类推.（1）试写出第n层所对应的点数；（2）试写出n层六边形点阵的总点数；（3）如果一个六边形点阵共有169个点，那么它一共有几层？6.如图，Rt△ABC中，∠B=90°，AC=10cm，BC=6cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以2cm/s的速度，沿AB向终点B移动；点Q以1cm/s的速度沿BC向终点C移动，其中一点到终点，另一点也随之停止．连接PQ．设动点运动时间为x秒．（1）用含x的代数式表示BQ、PB的长度；（2）当x为何值时，△PBQ为等腰三角形；（3）是否存在x的值，使得四边形APQC的面积等于20cm2？若存在，请求出此时x的值；若不存在，请说明理由．8. 如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上.直线CB的表达式为41633y x=-+，点A、D的坐标分别为（－4，0），（0，4）. 动点P从A点出发，在AB边上匀速运动. 动点Q从点B出发，在折线BCD上匀速运动，速度均为每秒1个单位长度. 当其中一个动点到达终点时，另一动点也停止运动. 设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ 的动点除外）.（1）求出点C的坐标；（2）求S随t变化的函数关系式；（3）当t为何值时，S有最大值？并求出这个最大值．（1）求抛物线的解析式；（2）在抛物线的对称轴上找到点M，使得M到D、B的距离之和最小，求出点M的坐标；（3）如果点P由点A出发沿线段AB以2cm/s的速度向点B运动，同时点Q由点B出发沿线段BC以1cm/s的速度向点C运动，当其中一点到达终点时，另一点也随之停止运动．设S=PQ2（cm2）．①求出S与运动时间t之间的函数关系式，并写出t的取值范围；10．已知：抛物线y ＝－x 2＋2x＋m-2交y 轴于点A （0，2m-7）．与直线y ＝x 交于点B 、C （B 在右、C在左）． （1）求抛物线的解析式；（2）设抛物线的顶点为E ，在抛物线的对称轴上是否存在一点F ，使得，若存在，求出点F 的坐标，若不存在，说明理由； （3）射线OC 上有两个动点P 、Q 同时从原点出发，分别以每秒个单位长度、每秒2个单位长度的速度沿射线OC 运动，以PQ 为斜边在直线BC 的上方作直角三角形PMQ （直角边分别平行于坐标轴），设运动时间为t 秒，若△PMQ 与抛物线y ＝－x 2＋2x ＋m-2有公共点，求t 的取值范围．11. 在平面直角坐标系中，抛物线经过A （－3,0）、B （4,0）两点，且与y 轴交于点C ，点D 在x 轴的负半轴上，且BD ＝BC ，有一动点P 从点A 出发，沿线段AB 以每秒1个单位长度的速度向点B 移动，同时另一个动点Q 从点C 出发，沿线段CA 以某一速度向点A 移动. （1）求该抛物线的解析式；（2）若经过t 秒的移动，线段PQ 被CD 垂直平分，求此时t 的值；2BFE CFE ∠=∠55xOy 42++=bx ax y（3）该抛物线的对称轴上是否存在一点M ，使MQ ＋MA 的值最小？若存在，求出点M 的坐标；若不存在，请说明理由.【答案与解析】 一、选择题 1．【答案】Ｂ；， ∴是二次函数图象，2．【答案】 A ． 21tan tan 2x x EFG x EFG ∠=∠2tan EFG ∠二、填空题3.【答案】1或3或； 【解析】解：∵抛物线y 1=2x 2向右平移2个单位，∴抛物线y 2的函数解析式为y=2（x-2）2=2x 2-8x+8，∴抛物线y 2的对称轴为直线x=2，∵直线x=t 与直线y=x 、抛物线y 2交于点A 、B ，∴点A 的坐标为（t ，t ），点B 的坐标为（t ，2t 2-8t+8），∴AB=|2t 2-8t+8-t|=|2t 2-9t+8|，AP=|t-2|，∵△APB 是以点A 或B 为直角顶点的等腰三角形，∴|2t 2-9t+8|=|t-2|，∴2t 2-9t+8=t-2 ①【解析】∵S 正方形OBAC =OB 2=9，∴OB=AB=3，∴点A 的坐标为（3，3）∵点A 在一次函数y=kx+1的图象上，5522+5.【答案与解析】解：（1）第n层上的点数为6（n －1）（n ≥2）．（2）n 层六边形点阵的总点数为＝1＋6＋12＋18＋…＋6(n －1)＝1＋＝3n(n －1)＋1．（3）令3n(n －1)＋1＝169，得n ＝8.所以，它一共是有8层．6.【答案与解析】7.【答案与解析】 2)1)](1(66[--+n n解：（１）１,２；（２）探索应用：设P （ｘ，），则C （ｘ，0），D （0，）， ∴CA ＝ｘ＋３，DB=+4, ∴S 四边形ABCD =CA ×DB=(x+3) ×(+4), 化简得：S=2(x+)+12， ∵x>0, >0,∴x+≥，只有当x=时，即x=3，等号成立.∴S ≥2×6+12=24,∴S 四边形ABCD 有最小值是24.此时，P(3，4),C(3，0),D(0，4),AB=BC=CD=DA=5，∴四边形是菱形.12x 12x12x121212x9x 9x 9x 9x＜t≤5时，（如图）①在0＜t ＜41(42OP QN =⨯1(2OP QN t =1(2OP OD t =②在4＜t≤5时，对于抛物线S ＝综合以上三种情况，当t=6时，S 取得最大值，最大值是4．9.【答案与解析】解：（1）据题意可知：A （0，2），B （2，2），C （2，0）．∵抛物线y=ax 2+bx+c 经过点A 、B 和D （4，）， 28285,225525t t t --=-=⨯当时，∴，∴，∴y=﹣x2+x+2；（2）点B关于抛物线的对称轴x=1的对称点为A．连接AD，与对称轴的交点即为M．∵A（0，2）、D（4，），∴直线AD的解析式为：y=﹣x+2，当x=1时，y=，则M（1，）；（3）①由图象知：PB=2﹣2t，BQ=t，AP=2t，∵在Rt△PBQ中，∠B=90°，∴S=PQ2=PB2+BQ2，∴=（2﹣2t）2+t2，即S=5t2﹣8t+4（0≤t≤1）．②当S=54时，54=5t2﹣8t+4即20t2﹣32t+11=0，解得：t=，t=＞1（舍）∴P（1，2），Q（2，）．PB=1．若R点存在，分情况讨论：（i）假设R在BQ的右边，如图所示，这时QR=PB，RQ∥PB，则R的横坐标为3，R的纵坐标为，即R（3，），代入y=﹣x2+x+2，左右两边相等，故这时存在R（3，）满足题意；（ii）假设R在PB的左边时，这时PR=QB，PR∥QB，则R（1，）代入y=﹣x2+x+2，左右两边不相等，则R不在抛物线上综上所述，存点一点R，以点P、B、Q、R为顶点的四边形只能是口PQRB．则R（3，）．此时，点R（3，）在抛物线=-x2+x+2上．10.【答案与解析】解：（1）点A（0，2m﹣7）代入y=﹣x2+2x+m﹣2，m﹣2=2m﹣7，解得：m=5故抛物线的解析式为y=﹣x2+2x+3；（2）如图1，由，得，∴B（，2），C（﹣，﹣2）B（，2），关于抛物线对称轴x=1的对称点为B′（2﹣，2），将B′，C代入y=kx+b，得：，解得：，可得直线B'C的解析式为：，由，可得，故当F（1，6）使得∠BFE=∠CFE；（3）如图2，当t秒时，P点横坐标为﹣t，则纵坐标为﹣2t，则M（﹣2t，﹣2t）在抛物线上时，可得﹣（﹣2t） 2﹣4t+3=﹣2t，整理得出：4t2+2t﹣3=0，解得：，当P（﹣t，﹣2t）在抛物线上时，可得﹣t2﹣2t+3=﹣2t，整理得出：t2=3，解得：，舍去负值，所以若△PMQ与抛物线y=﹣x2+2x+m﹣2有公共点t的取值范围是．11．【答案与解析】解：（1）∵抛物线y=ax2+bx+4经过A（﹣3，0），B（4，0）两点，∴，解得，∴所求抛物线的解析式为：y=﹣x2+x+4；（2）如图1，依题意知AP=t，连接DQ，∵A（﹣3，0），B（4，0），C（0，4），∴AC=5，BC=4，AB=7．∵BD=BC，∴AD=AB﹣BD=7﹣4，∵CD垂直平分PQ，∴QD=DP，∠CDQ=∠CDP．∵BD=BC，∴∠DCB=∠CDB．∴∠CDQ=∠DCB．∴DQ∥BC．∴△ADQ∽△ABC．∴=，∴=，∴=，解得DP=4﹣，∴AP=AD+DP=．∴线段PQ被CD垂直平分时，t的值为；（3）如图2，设抛物线y=﹣x2+x+4的对称轴x=与x轴交于点E．点A、B关于对称轴x=对称，连接BQ交该对称轴于点M．则MQ+MA=MQ+MB，即MQ+MA=BQ，∵当BQ⊥AC时，BQ最小，此时，∠EBM=∠ACO，∴tan∠EBM=tan∠ACO=，∴=，∴=，解ME=．∴M（，），即在抛物线y=﹣x2+x+4的对称轴上存在一点M（，），使得MQ+MA的值最小．。

代几综合题一直是大家的弱项，这个寒假希望同学们有所改善，考虑到大家自己找题很困难，故为同学们安排了练习，请认真完成！请先做56到75，再从1到55，其实题目都不错，只是后面的题目是近年的。

请同学们做的时候关注一下老师对题目的点评！请尽量不要移动图像，按照我排好的格式打印.1、图9是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息，解答下列问题：（1）汽车在前9分钟内的平均速度是多少？（2）汽车在中途停了多长时间？（3）当16≤t≤30时，求S与t的函数关系式.2、（04河北）如图15—1和15—2，在20×20的等距网格（每格的宽和高均是1个单位长）中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间为x秒，△QAC的面积为y.（1）如图15—1，当Rt△ABC向下平移到Rt△A1B1C1的位置时，请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形；（2）如图15—2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？（3）在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？点评：很好的一道和一次函数有关的点运动的问题！MB1AB图15—1ON PQ MCAB图15—23、记三角形三边长为a 、b 、c ，对应边上的高为a h 、b h 、c h ，请解答： （1）已知a h ：b h ：c h 4:3:2 ，且这三角形周长为26cm ，求a 、b 、c . （2）若三角形的三条高分别为2、x 、6，求x 的取值范围. （3）若三条高分别为2、x 、6的三角形是直角三角形，求x .（4）若三条高分别为2、x 、6的三角形是等腰三角形，求这等腰三角形的三边长. 点评：这种类型的题我们平时做的少，遇到了一定要弄明白！4、（04河北）探索下列问题：（1）在图12—1给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；（2）一条竖直方向的直线m 以及任意的直线n ，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S 1和S 2.①请你在图12—2中相应图形下方的横线上分别填写S 1与S 2的数量关系式（用“<”，“=”，“>”连接）； ②请你在图12—3中分别画出反映S 1与S 2三种大小关系的直线n ，并在相应图形下方的横线上分别填写S 1与S 2的数量关系式（用“<”，“=”，“>”连接）.（3）是否存在一条直线，将一个任意的平面图形（如图12—4）分割成面积相等的两部分，请简略说出理由.图12—1图12—3 图12—4图12—2图4 P N M CBA Oy x 5、（04上海）如图４，在△ABC 中，∠BAC ＝90°，延长BA 到点D ，使AD ＝21AB ，点E 、F 分别为边BC 、AC 的中点．（1）求证：DF=BE ；（2）过点A 作AG ∥BC ，交DF 于点G ，求证：AG=DG ．（无答案，自己证明）6、（04苏州）如图，平面直角坐标系中，四边形OABC 为矩形，点A 、B 的坐标分别为（3，0），（3，4）。

（3）当点P运动到什么位置时，四边形ABPC的面积最大，并求出此时P点的坐标和四边形ABPC的最大面积．
七、抛物线+图形变换+几何最值
【例8】（丰台）如图，将矩形 置于平面直角坐标系xOy中， ．
(1)抛物线 经过点B、C，求该抛物线的解析式；
(2)将矩形OABC绕原点顺时针旋转一个角度 ，在旋转过程中，当矩形的顶点落在(1)中的抛物线的对称轴上时，求此时这个顶点的坐标；
十三、抛物线+相似
【例15】（怀柔）如图，已知抛物线过点 ，且在 轴上截得 线段 长为 ，若顶点 的横坐标为 .
(1)求二次函数的解析式；
(2)在该抛物线的对称轴上找一点 ，使 最小，求出点 的坐标；
(3)在抛物线上是否存在点 ，使 与 相似？如果存在，求出点 的坐标；如果不存在，请说明理由．
（1）结合以上信息及图2填空：图2中的 ；
（2）求B、C两点的坐标及图2中OF的长；
（3）若OM是∠AOB的角平分线,且点G与点H分别是线段AO与射线OM上的两个动点，直接写出HG+AH的最小值，请在图3中画出示意图并简述理由。
8
二、动点+面积问题
【例2】 （门头沟）如图，在直角坐标系中，梯形 的底边AB在x轴上，底边CD的端点D在y轴上.直线CB的表达式为 ，点A、D的坐标分别为（－4，0），（0，4）.动点P从A点出发，在AB边上匀速运动.动点Q从点B出发，在折线BCD上匀速运动，速度均为每秒1个单位长度.当其中一个动点到达终点时，另一动点也停止运动.设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ的动点除外）.
五、等腰+动点与图形面积
【例5】 （平谷）如图，抛物线 与 轴交于点A(－2，0)和B(4，0)、与y轴交于点C．

初一下期终压轴题训练1.（10703黄陂区）如图，直线AB∥CD(1) 在图1中，∠BME、∠E、∠END的数量关系为（不需证明）在图2中，∠BMF、∠F、∠FND的数量关系为（不需证明）(2) 如图3，NE平分∠FND，MB平分∠FME，且2∠E及∠F互补，求∠FME的大小(3) 如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，E Q∥NP，则∠FE Q的大小是否发生变化，若变化，说明理由；若不变化，求∠FE Q的度数2（10704二中广雅）.如图1，已知直角梯形ABCO 中，∠AOC=90°，AB ∥x 轴，AB=6，若以点O 为原点，OA 、OC 所在直线为y 轴和x 轴建立如图所示直角坐标系，A （0，a),C(c,0）中，a ，c 满足0710=-+-+c c a（1）求出点A 、B 、C 的坐标；（2）如图2，若点M 从点C 出发，以2单位/秒的速度沿CO 方向移动，点N 从原点出发，以1单位/秒的速度沿OA 方向移动，设M 、N 两点同时出发，且运动时间为t 秒，当点N 从点O 运动到点A 时，点M 同时也停止运动，在它们的移动过程中，当2ABN OMBN S S ∆≤四边形时，求t 的取值范围；（3）如图3，若点N 是线段OA 延长线上一动点，∠NCH=k ∠OCH ，∠CNQ=k∠BNQ ，其中k>1，NQ ∥CJ ，求ABNHCJ∠∠的值（结果用含k 的式子表示）。

3(10701洪山区)如图，长方形ABCD在平面直角坐标系中，点A(1，8)，B(1，6)，C(7，6)，点X、Y分别在x、y轴上(1) 请直接写出D点的坐标_________(2) 连接线段OB、OD，OD交BC于E，∠BOY的平分线和∠BEO的平分线交于点F，若∠BOE＝n，求∠OFE的度数3个单位的速度向下运动，设运动的时间(3) 若长方形ABCD以每秒2为t秒，问在第一象限内是否存在某一时刻t，使△OBD的面积等于长方形ABCD的面积的？若存在，请求出t的值；若不存在，请说明理由4（10609二中周练六）平面直角坐标系中，A（a，b），B（2,2），且。

初三数学——代数与几何综合题【解题策略】1．认真审题，分析、挖掘题目的隐含条件，翻译并转化为显性条件；再将以上得到的显性条件进行恰当地组合，进一步得到新的结论．2．分析结构理清关系——注意题目的逻辑结构，搞清楚它的各个小题之间的关系是“平行”的，还是“递进”的．这一点非常重要．3．从代数几何两方面入手，多角度、多线索地深入分析，架起连接代数与几何的桥梁关键点．灵活运用数学思想方法，如数形结合思想、数学建模思想、分类讨论思想、转化的思想、函数与方程思想等．【题型特点】一、用函数的观点看方程（组）和不等式（组）1．若关于x 的一元二次方程2250ax x +-=的两根中有且仅有一根在0与1之间（不含0和1），则a 的取值范围是（ ）．A ．3a <B ．3a >C ．3a <-D ．3a >-2．直线y 1=kx +b 过点A （0，2），且与直线y 2=mx 交于点P （1，m ），则不等式组mx ＞kx+b ＞mx －2的解集是______________．二、图形运动中的函数关系这通常是先给定几何图形，根据已知条件进行计算，然后有动点（或动线段）运动，对应产生线段、面积等的变化（或不变化），求对应的未知函数（即在求出解析式前不确定函数的类型）的解析式和自变量的取值范围．求未知函数解析式的关键是列出包含自变量和因变量之间的等量关系．找等量关系的途径在初中主要有利用勾股定理、平行线截得比例线段、三角形相似等．求自变量的取值范围主要是寻找图形的特殊位置（极限位置）和根据解析式求解．1．（2010桂林）如图，已知正方形ABCD 的边长为4 ，E 是BC 边上的一个动点，AE ⊥EF ，EF 交DC 于F ，设BE =x ，FC =y ，则当点E 从点B 运动到点C 时，y 关于x 的函数图象是（ ）．A ．B ．C ．D ．ADBFMNABCD2．如图，已知△ABC 中，BC =8，BC 边上的高h=4，D 为BC 边上一个动点，EF ∥BC ，交AB 于点E ，交AC 于点F ，设E 到BC 的距离为x ，△DEF 的面积为y ，则y 关于x 的函数图象大致为（）．A ．B ．C ．D ．3．如图，在直角梯形ABCD 中，DC AB ∥，90A ∠=︒，28AB =cm ，24DC =cm ，4AD =cm ，点M 从点D 出发，以1cm/s 的速度向点C 运动，点N 从点B 同时出发，以2cm/s 的速度向点A 运动．当其中一个动点到达端点停止运动时，另一个动点也随之停止运动．则四边形ANMD 的面积2(cm )y 与两动点运动的时间(s)t 的函数图象大致是（）．A ．B ．C ．D ．4．如图，动点P 从点A 出发，沿线段AB 运动至点B 后，立即按原路返回，点P 在运动过程中速度大小不变，则以点A 为圆心，线段AP 长为半径的圆的面积S 与点P 的运动时间t 之间的函数图象大致为（ ）．5．（2010成都）如图，在ABC △中，90B ∠=︒，12mm AB =，24mm BC =，动点P 从点A 开始沿边AB 向B 以2mm /s 的速度移动（不与点B 重合），动点Q 从点B 开始沿边BC 向C 以4mm /s 的速度移动（不与点C 重合）．如果P 、Q 分别从A 、B 同时出发，那么经过_____________秒，四边形APQC 的面积最小．6．已知：如图（a），梯形ABCD中，AB∥CD，∠C＝90°，AB＝BC＝4，CD＝6．（1）E为BC边上一点，EF∥AD，交CD边于点F，FG∥EA，交AD边于点G，若四边形AEFG为矩形，求BE的长；（2）如图（b），将（1）中的∠AEF绕E点逆时针旋转为∠A′EF′，EF′交CD 边于F′点，且F′点与D点不重合，射线EA′交AB边于点M，作F′N∥EA′交AD边于点N，设BM为x，△NF′D中，F′D边上的高为y，求y关于x的函数解析式及自变量x的取值范围．图（a）图（b）7．如图，在Rt ABC∆中，90A∠=︒，6AB=，8AC=，D、E分别是边AB、AC的中点，点P从点D出发沿DE方向运动，过点P作PQ BC⊥于Q，过点Q作QR BA∥交AC于R，当点Q与点C重合时，点P停止运动．设BQ x=，QR y=．（1）求点D到BC的距离DH的长；（2）求y关于x的函数关系式（不要求写出自变量的取值范围）；（3）若点P使PQR∆为等腰三角形．请直接写出所有满足要求的x的值．AB CD ERPH Q三、坐标几何问题这通常是先给定直角坐标系和几何图形，求已知函数（即在求出解析式前就已知函数的类型）的解析式，然后进行图形的研究，求点的坐标或研究图形的某些性质．然后根据所求的函数关系进行探索研究，探索研究的一般类型有：①在什么条件下三角形是等腰三角形、直角三角形；②四边形是菱形、梯形等；③探索两个三角形满足什么条件相似；④探究线段之间的位置关系等；⑤探索面积之间满足一定关系求x 的值等；⑥直线（圆）与圆的相切时求自变量的值等．求已知函数的解析式主要方法是待定系数法，关键是求点的坐标，而求点的坐标基本方法是几何法（图形法）和代数法（解析法）．1．（2009十堰）已知函数1y x =-+的图象与x 轴、y 轴分别交于点C 、B ，与双曲线xky =交于点A 、D ，若AB+CD= BC ，则k 的值为 ．2．（2010义乌）（1）将抛物线y 1＝2x 2向右平移2个单位，得到抛物线y 2的图象，则y 2= ；（2）如图，P 是抛物线y 2对称轴上的一个动点，直线x ＝t 平行于y 轴，分别与直线y ＝x 、抛物线y 2交于点A 、B ．若△ABP 是以点A 或点B 为直角顶点的等腰直角三角形，求满足条件的t 的值，则t ＝ ．3．如图，在等腰梯形ABCD 中，AD BC ∥，5AB DC ==，6AD =，12BC =．动点P 从D 点出发沿DC 以每秒1个单位的速度向终点C 运动，动点Q 从C 点出发沿CB 以每秒2个单位的速度向B 点运动．两点同时出发，当P 点到达C点时，Q 点随之停止运动．（1）梯形ABCD 的面积等于 ；（2）当PQ AB ∥时，P 点离开D 点的时间等于 秒；（3）当P Q C ，，三点构成直角三角形时，P 点离开D 点的时间是 秒．Cxx4．（2009武汉）如图，抛物线y＝ax2＋bx－4a经过A（－1，0），C（0，4）两点，与x轴交于另一点B．（1）求抛物线的解析式；（2）已知点D（m，m＋1）在第一象限的抛物线上，求点D关于直线BC对称的点E的坐标；（3）在（2）的条件下，连接BD，若点P为抛物线上一点，且∠DBP＝45°，求点P的坐标．与x轴只有一个公共点．（1）求这个函数关系式；2+x+1图象的（2）如图所示，设二次．．函数y=ax顶点为B，与y轴的交点为A，P为图象上的一点，若以线段PB为直径的圆与直线AB相切于点B，求P点的坐标；（3）在（2）中，若圆与x轴另一交点关于直线PB的对称点为M，试探索点M是否在抛物线y=ax2+x+1上，若在抛物线上，求出M点的坐标；若不在，请说明理由．6．（2008常州）如图，抛物线24y x x =+与x 轴分别相交于点B 、O ，它的顶点为A ，连接AB ，把AB 所的直线沿y 轴向上平移，使它经过原点O ，得到直线l ，设P 是直线l 上一动点．（1）求点A 的坐标；（2）以点A 、B 、O 、P 为顶点的四边形中，有菱形、等腰梯形、直角梯形，请分别直接写出这些特殊四边形的顶点P 的坐标；（3）设以点A 、B 、O 、P 为顶点的四边形的面积为S ，点P 的横坐标为x，当46S +≤≤+x 的取值范围．7．如图，已知抛物线与x 轴交于点(2 0)A -，，(4 0)B ，，与y 轴交于点(0 8)C ，．（1）求抛物线的解析式及其顶点D 的坐标；（2）设直线CD 交x 轴于点E ．在线段OB 的垂直平分线上是否存在点P ，使得点P 到直线CD 的距离等于点P 到原点O 的距离？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）过点B 作x 轴的垂线，交直线CD 于点F ，将抛物线沿其对称轴平移，使抛物线与线段EF 总有公共点．试探究：抛物线向上最多可平移多少个单位长度？8．如图，在平面直角坐标系中，直线)0(21>+-=b b x y 分别交x 轴，y 轴于A ，B两点，以OA ，OB 为边作矩形OACB ，D 为BC 的中点．以M （4，0），N （8，0）为斜边端点作等腰直角三角形PMN ，点P 在第一象限，设矩形OACB 与△PMN 重叠部分的面积为S ．（1）求点P 的坐标；（2）当b 值由小到大变化时，求S 与b 的函数关系式；（3）若在直线b x y +-=21（b ＞0）上存在点Q ，使∠OQM 等于90°，请直接写出．．．．b 的取值范围；（4）在b 值的变化过程中，若△PCD 为等腰三角形，请直接写出．．．．所有符合条件的b 值．【中考汇编】1．（2009 山西省太原市） 如图，AB 是半圆O 的直径，点P 从点O 出发，沿 OA AB BO --的路径运动一周．设OP 为s ，运动时间为t ，则下列图形能大致地刻画s 与t 之间关系的是（ ）．2．（2008 盐城） 如图，A 、B 、C 、D 为⊙O 的四等分点，动点P 从圆心O 出发，沿O — C — D — O 路线作匀速运动．设运动时间为t （s ），∠APB =y （°），则下列图象中表示y 与t 之间函数关系最恰当的是（ ）．OPDCBAA ．B ．C ．D ．3．（2010 南京）如图，夜晚，小亮从点A 经过路灯C 的正下方沿直线走到点B ，他的影长y 随他与点A 之间的距离x 的变化而变化，那么表示y 与x 之间函数关系的图象大致为（ ）．4．（2009 湖北省襄樊市） 在ABC △中，12cm 6cm AB AC BC D ===，，为BC 的中点，动点P 从B 点出发，以每秒1cm 的速度沿B A C →→的方向运动．设运动时间为t ，那么当t = 秒时，过D 、P 两点的直线将ABC △的周长分成两个部分，使其中一部分是另一部分的2倍．5．（2009天津市）已知一个直角三角形纸片OAB ，其中90AOB ∠=︒，2OA =，4OB =．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D ．（1）若折叠后使点B 与点A 重合，求点C 的坐标；B ．C．A ．D ．AB ．C ．D（2）若折叠后点B 落在边OA 上的点为B '，设O B x '=，OC y =，试写出y 关于x 的函数解析式，并确定y 的取值范围；（3）若折叠后点B 落在边OA 上的点为B '，且使B D OB '∥，求此时点C 的坐标．6．（2009 云南省昆明市） 如图，在平面直角坐标系中，四边形OABC 是梯形，OA ∥BC ，点A 的坐标为（6，0），点B 的坐标为（4，3），点C 在y 轴的正半轴上．动点M 在OA 上运动，从O 点出发到A 点；动点N 在AB 上运动，从A 点出发到B 点．两个动点同时出发，速度都是每秒1个单位长度，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t （秒）．（1）求线段AB 的长；当t 为何值时，MN ∥OC ？ （2）设△CMN 的面积为S ，求S 与t 之间的函数解析式，并指出自变量t 的取值范围；S 是否有最小值？若有最小值，最小值是多少？（3）连接AC ，那么是否存在这样的t ，使MN 与AC 互相垂直？若存在，求出这时的t 值；若不存在，请说明理由．7．（2010 内蒙古鄂尔多斯市） 如图，四边形OABC 是一张放在平面直角坐标系的矩形纸片，O 为原点，点A 在x 轴上，点C 在y 轴上，159OA OC ==，，在AB 上取一点M ，使得CBM △沿CM 翻折后，点B 落在x 轴上，记作N 点． （1）求N 点、M 点的坐标； （2）将抛物线236y x =-向右平移(010)a a <<个单位后，得到抛物线l ，l 经过N 点，求抛物线l 的解析式； （3）①抛物线l 的对称轴上存在点P ，使得P 点到M N ，两点的距离之差最大，求P 点的坐标；②若点D 是线段OC 上的一个动点（不与O 、C 重合），过点D 作DE OA ∥交CN 于E ，设CD 的长为m ，PDE △的面积为S ，求S 与m 之间的函数关系式，并说明S 是否存在最大值．若存在，请求出最大值；若不存在，请说明理由．8．（2010 江苏省徐州市）如图①，将边长为4cm 的正方形纸片ABCD 沿EF 折叠（点E 、F 分别在边AB 、CD 上），使点B 落在AD 边上的点M 处，点C 落在点N 处，MN 与CD 交于点 P ，连接EP ．（1）如图②，若M 为AD 边的中点，①△AEM 的周长= cm ；②求证：EP=AE +DP ；（2）随着落点M 在AD 边上取遍所有的位置（点M 不与A 、D 重合），△PDM 的周长是否发生变化？请说明理由．x9．（2010 青海省西宁市） 如图，直线y =kx －1与x 轴、y 轴分别交与B 、C 两点，tan ∠OCB =21．（1）求B 点的坐标和k 的值；（2）2若点A （x ，y ）是第一象限内的直线y =kx －1上的一个动点.当点A 运动过程中，试写出△AOB 的面积S 与x 的函数关系式；（3）探索：①当点A 运动到什么位置时，△AOB 的面积是41；②在①成立的情况下，x 轴上是否存在一点P ，使△POA 是等腰三角形.若存在，请写出满足条件的所有P 点的坐标；若不存在，请说明理由．10．（2010 福建省龙岩市） 如图①，将直角边长为ABC 绕其直角顶点C 顺时针旋转α角()090α<<°°，得111ABC AC △，交AB 于点D ，11A B 分别交于BC AB 、于点E F 、，连接1AB ．（1）求证：ADC ∆∽1A DF ∆； （2）若30α=°，求11AB A ∠的度数；（3）如图②，当45α=°时，将11A B C △沿C A →方向平移得22222A B C A C △，交AB于点G ，22B C 交BC 于点H ，设2CC x =（0x <<，ABC △与222A B C △的重叠部分面积为S ，试求S 与x 的函数关系式．11．（2009福建省泉州市）在直角坐标系中，点(50)A ，关于原点O 的对称点为点C ． （1）请直接写出点C 的坐标； （2）若点B 在第一象限内，∠OAB =∠OBA ，并且点B 关于原点O 的对称点为点D ． ①试判断四边形ABCD 的形状，并说明理由；②现有一动点P 从B 点出发，沿路线BA —AD 以每秒1个单位长的速度向终点D 运动，另一动点Q 从A 点同时出发，沿AC 方向以每秒0.4个单位长的速度向终点C 运动，当其中一个动点到达终点时，另一个动点也随之停止运动．已知AB =6，设点P 、Q 的运动时间为t 秒，在运动过程中，当动点Q 在以PA 为直径的圆上时，试求t 的值．12．（2009 上海市） 在直角坐标平面内，O为原点，点A 的坐标为(10)，，点C 的坐标为(04)，，直线CM x ∥轴（如图所示）．点B 与点A 关于原点对称，直线y x b =+（b 为常数）经过点B ，且与直线CM 相交于点D ，联结OD ．（1）求b 的值和点D 的坐标；（2）设点P 在x 轴的正半轴上，若POD △是等腰三角形，求点P 的坐标；（3）在（2）的条件下，如果以PD 为半径的圆P 与圆O 外切，求圆O 的半径．13．（2010 宁夏回族自治区） 如图，已知：一次函数：4y x =-+的图像与反比例函数：2y x=(0)x >的图像分别交于A 、B 两点，点M 是一次函数图像在第一象限部分上的任意一点，过M 分别向x 轴、y 轴作垂线，垂足分别为M 1、M 2，设矩形MM 1OM 2的面积为S 1；点N 为反比例函数图像上任意一点，过N 分别向x 轴、y 轴作垂线，垂足分别为N 1、N 2，设矩形NN 1ON 2的面积为S 2；（1）若设点M 的坐标为（x ，y ），请写出S 1关于x 的函数表达式，并求x 取何值时，S 1的最大值；（2）观察图形，通过确定x 的取值，试比较S 1、S 2的大小． 14．（2010四川省眉山市）如图，Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上，O 为原点，A 、B 两点的坐标分别为（－3，0）、（0，4），x抛物线223y x bx c =++经过B 点，且顶点在直线52x =上．（1）求抛物线对应的函数关系式；（2）若△DCE 是由△ABO 沿x 轴向右平移得到的，当四边形ABCD 是菱形时，试判断点C 和点D 是否在该抛物线上，并说明理由；（3）若M 点是CD 所在直线下方该抛物线上的一个动点，过点M 作MN 平行于y 轴交CD 于点N ．设点M 的横坐标为t ，MN 的长度为l ．求l 与t 之间的函数关系式，并求l 取最大值时，点M 的坐标．15．（2010四川省内江市）如图，抛物线()2230y mx mx m m =-->与x 轴交于A B 、两点，与y 轴交于C 点．（1）请求出抛物线顶点M 的坐标（用含m 的代数式表示），A B 、两点的坐标；（2）经探究可知，BCM △与ABC △的面积比不变，试求出这个比值；（3）是否存在使BCM △为直角三角形的抛物线？若存在，请求出；如果不存在，请说明理由．x16．（2010四川省南充市）已知抛物线2142y x b x =-++上有不同的两点E （3k +，21k -+）和F （1k --，21k -+）．（1）求抛物线的解析式．（2）如图，抛物线2142y x bx =-++与x 轴和y 轴的正半轴分别交于点A 和B ，M 为AB 的中点，∠PMQ 在AB 的同侧以M 为中心旋转，且∠PMQ ＝45°，MP 交y 轴于点C ，MQ 交x 轴于点D ．设AD 的长为m （m ＞0），BC 的长为n ，求n 和m 之间的函数关系式．（3）当m ，n 为何值时，∠PMQ 的边过点F ． 17．（2009浙江省湖州市）如图，在平面直角坐标系中，直线l ∶y =28x --分别与x 轴，y 轴相交于A B ，两点，点()0P k ，是y 轴的负半轴上的一个动点，以P 为圆心，3为半径作P ⊙．（1）连结PA ，若PA PB =，试判断P ⊙与x 轴的位置关系，并说明理由；（2）当k 为何值时，以P ⊙与直线l 的两个交点和圆心P 为顶点的三角形是正三角形？18．（2010湖南省湘潭市）如图，直线6=-+与x轴交于点A，与y轴交于点B，y x以线段AB为直径作⊙C，抛物线c=2过A、C、O三点．+bxy+ax（1）求点C的坐标和抛物线的解析式；（2）过点B作直线与x轴交于点D，且OB2=OA·OD，求证：DB是⊙C的切线；（3）抛物线上是否存在一点P，使以P、O、C、A为顶点的四边形为直角梯形，如果存在，求出点P的坐标；如果不存在，请说明理由．Array19．（2010湖南省株洲市）在平面直角坐标系中，抛物线过原点O，且与x轴交于另一点A，其顶点为B．孔明同学用一把宽为3cm带刻度的矩形直尺对抛物线进行如下测量：①量得3=；OA cm②把直尺的左边与抛物线的对称轴重合，使得直尺左下端点与抛物线的顶点重合（如图1），测得抛物线与直尺右边的交点C的刻度读数为4.5．请完成下列问题：（1）写出抛物线的对称轴； （2）求抛物线的解析式；（3）将图中的直尺（足够长）沿水平方向向右平移到点A 的右边（如图2），直尺的两边交x 轴于点H 、G ，交抛物线于点E 、F ．求证：21(9)6EFGH S EF =-梯形． 20．（2010湖北省十堰市）已知关于x 的方程2(31)220mx m x m --+-=． （1）求证：无论m 取任何实数时，方程恒有实数根．（2）若关于x 的二次函数2(31)22y mx m x m =--+-的图象与x 轴两交点间的距离为2时，求抛物线的解析式．（3）在直角坐标系xoy 中，画出（2）中的函数图象，结合图象回答问题：当直线图 1图2· By x b =+与（2）中的函数图象只有两个交点时，求b 的取值范围．21．（2010广西河池市） 如图，在直角梯形OABC 中，CB ∥OA ，90OAB ∠=︒，点O 为坐标原点，点A 在x 轴的正半轴上，对角线OB ，AC 相交于点M ，4OA AB ==，2OA CB =．（1）线段OB 的长为 ，点C 的坐标为 ；（2）求△OCM 的面积；（3）求过O ，A ，C 三点的抛物线的解析式； （4）若点E 在（3）的抛物线的对称轴上，点F 为该抛物线上的点，且以A ，O ，F ，E 四点为顶点的四边形为平行四边形，求点F 的坐标．22．（2010 江苏省苏州市）如图，以A 为顶点的抛物线与y 轴交于点.B 已知A B 、两点的坐标分别为（3，0）、（0，4）．（1）求抛物线的解析式；（2）设()M m n ，是抛物线上的一点（m n 、为正整数），且它位于对称轴的右侧.若以M B O A 、、、为顶点的四边形四条边的长度是四个连续的正整数，求点M 的坐标；（3）在（2）的条件下，试问：对于抛物线对称轴上的任意一点P ，22228PA PB PM ++>是否总成立？请说明理由．23．（2010浙江省丽水市）△ABC 中，∠A =∠B =30°，AB =．把△ABC 放在平面直角坐标系中，使AB 的中点位于坐标原点O （如图），△ABC 可以绕点O 作任意角度的旋转．（1）当点B 在第一象限，纵坐标是B 的横坐标；（2）如果抛物线2y ax bx c =++（a ≠0）的对称轴经过点C ，请你探究：①当a =12b =-，c =A ，B 两点是否都在这条抛物线上？并说明理由；②设b =－2am ，是否存在这样的m 的值，使A ，B 两点不可能同时在这条抛物线上？若存在，直接写出m 的值；若不存在，请说明理由．24．（2010新疆乌鲁木齐）已知二次函数2(0)y ax bx c a =++≠的图象经过(00)(1)O M ，，，1和()(0)N n n ≠，0三点．（1）若该函数图象顶点恰为点M ，写出此时n 的值及y 的最大值；（2）当2n =-时，确定这个二次函数的解析式，并判断此时y 是否有最大值； （3）由（1）、（2）可知，n 的取值变化，会影响该函数图象的开口方向.请你求出n 满足什么条件时，y 有最小值？25．（2009沈阳）如图所示，在平面直角坐标系中，点O 为坐标原点．Rt △OBA 的斜边OA 在x 轴的正半轴上，点A 的坐标为（2，0），点B 在第一象限内，且3=OB ，∠OBA ＝90°．沿边OB 所在直线折叠Rt △OAB ，记点A 的落点为C ．（1）求证：△OAC 为等边三角形；（2）点D 在x 轴的正半轴上，且点D 的坐标为（4，0），P 为线段OC 上一动点（点P 不与点O 重合），连接P A ，PD ，设PC ＝x ，△P AD 的面积为y ，求y 与x 之间的函数关系式；（3）在（2）的条件下，当21=x 时，过点A 作AM ⊥PD 于点M ，若PDAMk 27=，求证：二次函数y ＝k x k x 3)337(22+---的图象关于y 轴对称．26．如图（a），正方形ABCD的顶点A，B的坐标分别为（0，10），（8，4），顶点C，D在第一象限．点P从点A出发，沿正方形按逆时针方向匀速运动，同时点Q从点E（4，0）出发，沿x轴正方向以相同速度运动．当点P到达点C时，P，Q两点同时停止运动，设运动的时间为t秒．（1）求正方形ABCD的边长；（2）当点P在AB边上运动时，△OPQ的面积S（平方单位）与时间t（秒）之间的函数图象为抛物线的一部分（如图（b）所示），求P，Q两点的运动速度；（3）求（2）中面积S（平方单位）与时间t（秒）的函数关系式及面积S取最大值时点P的坐标；（4）求出图（b）中a，b的值．27．已知如图，四边形OABC是一张放在平面直角坐标系中的正方形纸片，点O 与坐标原点重合，点A在x轴的正半轴上，点C在y轴的正半轴上，OC＝4，E为BC 的中点，点N的坐标为（3，0），过点N且平行于y轴的直线MN与EB交于点M，现将纸片沿过E点的直线折叠，使顶点C落在MN上，落点记为G，折痕与y轴的交点记为F．（1）求点G的坐标；（2）求折痕EF所在直线的解析式；（3）设点P 为直线EF 上的点，是否存在这样的点P ，使得以P ，F ，G 为顶点的三角形为等腰三角形?若存在，直接写出点P 的坐标；若不存在，请说明理由．28．（2009黄冈）如图，在平面直角坐标系xOy 中，抛物10941812--=x x y 与x 轴正半轴的交点为A ，与y 轴的交点为B ，过点B 作x 轴的平行线BC ，交抛物线于点C ，连接AC ．现有两动点P ，Q 分别从O ，C 两点同时出发，点P 以每秒4个单位的速度沿OA 向终点A 移动，点Q 以每秒1个单位的速度沿CB 向点B 移动，点P 停止运动时，点Q 也同时停止运动，线段OC ，PQ 相交于点D ，过点D 作DE ∥OA ，交CA 于点E ，射线QE 交x 轴于点F ．设动点P ，Q 移动的时间为t （单位：秒）．（1）求A ，B ，C 三点的坐标和抛物线的顶点坐标；（2）当t 为何值时，四边形PQCA 为平行四边形？请写出计算过程；（3）当290<<t 时，△PQF 的面积是否总为定值？若是，求出此定值；若不是，请说明理由；（4）当t 为何值时，△PQF 为等腰三形？请写出解答过程．。

数学竞赛中的函数与平行四边形问题
总结词：数学竞赛
详细描述：在数学竞赛中，函 数与平行四边形问题是一个常 见的考点。这类问题通常需要 考生灵活运用代数、几何和解 析几何的知识，通过构造、推 理和证明来解答。解决这类问 题需要考生具备扎实的数学基 础和良好的思维能力。
学科交叉的函数与平行四边形问题
详细描述：函数与平行四边形问题可以与其他学科领域进行交叉融合， 如物理学、工程学、计算机科学等。通过学科交叉，可以产生许多具 有挑战性和实际意义的问题，推动数学和其他学科的发展。解决这类 问题需要跨学科的知识和思维方式，能够培养考生的综合素质和创新 能力。 总结词：学科交叉
性质
函数具有确定性、可重复性和有界性。确定性表示对于输入的每一个值，函数都有 唯一的输出值与之对应；可重复性表示相同的输入总是产生相同的输出；有界性表
平行四边形的定义与性质
平行四边形是一个四边形， 其中相对的两边平行。 定义 平行四边形具有对边平行、 对角相等、对角线互相平 分等性质。 性质
函数与平行四边形的关联
利用函数的单调性判断平行四边形的变化趋势
根据函数在某区间的单调性，判断平行四边形 面积或周长的变化趋势。
对于具有周期性关系。
函数与平行四边形的综合问题解析
结合几何与代数知识
在解决函数与平行四边形综合问题时， 需要综合运用几何和代数知识，如三 角函数、向量、解析几何等。
Annual Work Summary Report
2021
2022
2023
目录
O1 单击 C添O加N文TE本NTS
O2
单击 添加文本
O3
单击 添加文本
#O1
函数与平行四边 形的基本概念

图28－1
专题八┃ 京考解读
m－1 2 5m 解： (1)∵抛物线 y＝－ x ＋ x＋m2－3m＋2 经过原点， 4 4 ∴m2－3m＋2＝0.解得 m1＝1，m2＝2. 由题意知 m≠1，∴m＝2. 1 2 5 ∴抛物线的解析式为 y＝－ x ＋ x. 4 2 1 2 5 ∵点 B(2，n)在抛物线 y＝－ x ＋ x 上， 4 2 ∴n＝4. ∴B 点的坐标为 (2，4).
专题八┃ 京考解读
解： (1)①∵B 为 y 轴上的一个动点， ∴设点 B 的坐标为(0，y)． 1 1 ∵－ －0 ＝ ≠2， 2 2 ∴|0－y|＝2， 解得 y＝2 或 y＝－2. ∴点 B 的坐标是(0，2)或(0，－2)． 1 ②点 A 与点 B 的“非常距离”的最小值为 . 2
专题八┃ 京考解读
②依题意作等腰直角三角形 QMN. 设直线 AB 的解析式为 y＝k2x＋b. 由点 A(10，0)，点 B(2，4)，求得直线 AB 的解析式为 1 y＝－ x＋5.当 P 点运动到 t 秒时，两个等腰直角三角形分别 2 有一条边恰好落在同一条直线上，有以下三种情况： 第一种情况：CD 与 NQ 在同一条直线上，如图②.可 证△DPQ 为等腰直角三角形． 此时 OP、DP、AQ 的长 可依次表示为 t、4t、2t 个单位． ∴PQ＝DP＝4t. 10 ∴t＋4t＋2t＝10.∴t＝ . 7
专题八┃ 京考解读
(2)由(1)可得点 M 的坐标为(0，6 3)．由 DE∥AB，EM＝MD， 可得 y 轴所在直线是线段 ED 的垂直平分线． ∴点 C 关于直线 DE 的对称点 F 在 y 轴上． ∴ED 与 CF 互相垂直平分．∴CD＝DF＝FE＝EC. ∴四边形 CDFE 为菱形，且点 M 为其对称中心． 作直线 BM.设 BM 与 CD、EF 分别交于点 S、点 T. 可证△FTM≌△CSM. ∴FT＝CS.∵FE＝CD，∴TE＝SD. ∵EC＝DF，∴TE＋EC＋CS＋ST＝SD＋DF＋FT＋TS. ∴直线 BM 将四边形 CDFE 分成周长相等的两个四边形． ∵点 B(6，0)，点 M(0，6 3)在直线 y＝kx＋b 上， ∴直线 BM 的解析式为 y＝－ 3x＋6 3.