当前位置：文档之家 › 逻辑函数及其化简

逻辑函数及其化简

  • 格式：ppt
  • 大小：980.50 KB
  • 文档页数：77

下载文档原格式

  / 77

合集下载

第二章 逻辑函数及其简化

第二章 逻辑函数及其简化


L 表示。
利用反演规则，可以非常方便地求得一个函数的反函数 求函数 L AC B D 的反函数：
解： L ( A C) ( B D) 例 求函数 解：
L A B D
在应用反演规则求反函数时要注意以下两点： （1）保持运算的优先顺序不变，必要时加括号表明；
A B
如：串联开关电路
逻辑符号和表达式
A B C
P
P = A ·B · C=A×B ×C = A B C
&
真值表：列出输入的所
有状态和输出值。
逻辑1: 表示开关”闭”,灯的” 亮”. 逻辑0: 表示开关”断”,灯的”
A B
断 断 断 闭 闭 断 闭 闭
P
灭 灭 灭 亮
A B 0 0 0 1 1 0 1 1
B
逻辑符号和表达式
A B C ≥1
真值表：
A B 0 0 0 1 P 0 1 1 1
P = A + B+ C
或逻辑也称逻辑加运算，相当于 集合中的并集，根据并集的概念， 不难确定逻辑加的运算规则： A+B = P 0+ 0 = 0 0+ 1 = 1 1+ 0 = 1
A B P 00 0 0 1 1 1 0 1
第二章 逻辑函数及其简化
2.1 基本概念
2.2 逻辑代数 2.3 逻辑函数的表示方法 2.4 代数法化简逻辑函数 2.5 逻辑函数的卡诺图化简
2.1 基本概念
逻辑门电路：在数字电路中，实现逻辑运算功能的电路。 如：与门、或门、非门。 逻辑状态：在数字电路中；把一个状态分为两种，一种 状态叫逻辑1，另一种状态叫逻辑0 。
名称
第二章-逻辑函数及其简化

第二章-逻辑函数及其简化


A 0 0 1 1
B 0 1 0 1
Y 1 0 0 1
例2 有X、Y、Z三个输入变量，当其中两个或两个以上取值 为1时，输出F为1；其余输入情况输出均为0。试写出描述此 问题的逻辑函数表达式。 解：三个输入变量有23=8种不同组合，根据已知条件可得真值表 如 下：
由真值表可知，使F=1的输入变量组合有4个，所以F的与—或 表达式为：
F XYZ X Y Z XY Z XYZ
2）逻辑函数的表示方法
（1）真值表 逻辑函数的真值表具有唯一性。逻辑函数有n个变量时， 共有2n个不同的变量取值组合。在列真值表时，变量取值 的组合一般按n位二进制数递增的方式列出。用真值表表 示逻辑函数的优点是直观、明了，可直接看出逻辑函数值 和变量取值之间的关系。
对偶关系
A(A+B)=AB
4）包含律
证明：
AB+AC+BC=AB+AC
AB+AC+BC =AB+AC+(A+A)BC =AB+AC+ABC+ABC =AB(1+C)+AC(1+B) =AB+AC
对偶关系
5) 关于异或和同或运算
对偶数个变量而言， 有 A1A2... An=A1 A2 ... An
对奇数个变量而言， 有 A1A2... An=A1 A2 ... An
异或和同或的其他性质:
A 0= A 1= A A= A (B C)=(A B ) C A (B C)=AB AC
A 1=A A 0 =A A A= 1 A (B C)=(A B) C A+(B C )=(A+B) (A+C)
第1章(2课) 逻辑函数常用公式和化简

第1章(2课) 逻辑函数常用公式和化简

（２）利用公式Ａ＋Ａ＝Ａ，为某项配上其所能合并的项。
Y ABC ABC AB C A BC ( ABC ABC ) ( ABC AB C ) ( ABC A BC) AB AC BC
４、消去冗余项法
利用冗余律ＡＢ＋ＡＣ＋ＢＣ＝ＡＢ＋ＡＣ， 将冗余项ＢＣ消去。
Y ( A, B, C, D) m(1,3,4,6,7,11 ,14,15)
AB CD 00 00 01 11 10 0 1 1 0 01 1 0 1 1 11 0 0 1 1 10 0 0 1
m1 m3
m4
m11
m7
m15
0
m6
m14
（2）逻辑函数以一般的逻辑表达式给出：先将函数变换为与或 表达式（不必变换为最小项之和的形式），然后在卡诺图上与每 一个乘积项所包含的那些最小项（该乘积项就是这些最小项的公 因子）相对应的方格内填入1，其余的方格内填入0。
2、吸收法 （１）利用公式Ａ＋ＡＢ＝Ａ，消去多余的项。 是另 项 是 Y1 A B A BCD( E F ) A B 多外 的 另 运用摩根定律 余 一 因 外 如 的个 子 一 果 。乘 ， 个 乘 Y2 A B CD ADB A BCD AD B 积则乘积 项这积项 ( A AD) ( B BCD) A B （２）利用公式Ａ＋ＡＢ＝Ａ+Ｂ，消去多余的变量。 因项 的 Y AB C A C D BC D 子 的 反 Y AB A C B C 如 AB C C ( A B) D 是 因 是 果 多子 另 一 AB ( A B )C 余， 一 个 AB C ( A B) D 的则 个 乘 AB ABC AB C AB D 。这 乘 积 AB C 个积项 AB C D
2 逻辑函数及其化简

2 逻辑函数及其化简


1 1 1 1 1 1
AD
B
11
A 冗余项
AC
10
∴ F2 ( A, B, C, D) = AB + BC + AD
C
AB
例：用公式化简法得到下式，问是否最简， 若不是请化简之。
F3 ( A , B, C) = A B + AC + AB + BC
填项：
A
0 1
BC00
C
01 1 11 1 10
1
第二章 逻辑代数基础
§2.1 逻辑代数运算法则 §2.2 逻辑函数的化简 §2.3 卡诺图法
§2.1 逻辑代数运算法则
依据： 1.逻辑变量只取：0 、1两种状态。 2.与、或、非是三种最基本的逻辑运算。 与普通代数运算法则类似的：分配 律、结合律、交换律等。 与普通代数运算法则不同的： A•A=A A+A=A A = A (还原律）
= B + BD + ABD + ABCD
吸收消去
= B + BD
（长中含短，留下短）
吸收消去 （长中含反，去掉反） ∴F1 = B + D（最简与或式）
F2 = AD + AD + AB + AC + BD + ACEF+ BEF + DEFG
A
吸收消去 （长中含短，留下短）
(合并项)
= A + AC + BD + BEF + DEFG
ABD
D
01
（ + C) C
直接填入
11
10
01 11
1
1
B A
逻辑函数化简公式大全

逻辑函数化简公式大全

逻辑函数化简公式大全逻辑函数化简是在布尔代数中常用的一种方法，它通过应用逻辑运算规则和布尔代数定律，将复杂的逻辑函数简化为更简洁的形式。

这种简化可以减少逻辑电路的复杂性，提高计算机系统的效率。

以下是一些常见的逻辑函数化简公式大全：1. 与运算的化简：- 与运算的恒等律：A∧1 = A，A∧0 = 0- 与运算的零律：A∧A' = 0，A∧A = A- 与运算的吸收律：A∧(A∨B) = A，A∧(A∧B) = A∧B- 与运算的分配律：A∧(B∨C) = (A∧B)∨(A∧C)- 与运算的交换律：A∧B = B∧A2. 或运算的化简：- 或运算的恒等律：A∨1 = 1，A∨0 = A- 或运算的零律：A∨A' = 1，A∨A = A- 或运算的吸收律：A∨(A∧B) = A，A∨(A∨B) = A∨B- 或运算的分配律：A∨(B∧C) = (A∨B)∧(A∨C)- 或运算的交换律：A∨B = B∨A3. 非运算的化简：- 非运算的双重否定律：(A) = A- 非运算的德摩根定律：(A∧B) = A∨B，(A∨B) = A∧B4. 异或运算的化简：- 异或运算的恒等律：A⊕0 = A，A⊕1 = A- 异或运算的自反律：A⊕A = 0- 异或运算的结合律：A⊕(B⊕C) = (A⊕B)⊕C- 异或运算的交换律：A⊕B = B⊕A5. 条件运算的化简：- 条件运算的恒等律：A→1 = 1，A→0 = A- 条件运算的零律：A→A' = 0，A→A = 1- 条件运算的反转律：A→B = A∨B- 条件运算的分配律：A→(B∧C) = (A→B)∧(A→C)这些公式是逻辑函数化简中常用的基本规则，通过灵活应用它们，可以将复杂的逻辑表达式简化为更简单的形式。

使用这些规则，我们可以提高逻辑电路的效率和简洁性，并降低硬件成本。

逻辑函数及其简化

逻辑函数及其简化


消去法
运用吸收律 A AB A B 消去多余因子。
L A AB BE A B BE ABE
L AB AC BC
AB A B C
AB ABC
AB C
AB AB C C ABC ABC
AB AC AB AC BC
将某一乘积项展开为两项，或添加某乘积项，再与其它乘积项 进行合并化简。
AB
A
C 00 01 11 10
00 0 1 0
C1 0 1 1 1
B
从逻辑表达式到卡诺图
（1）如果表达式为最小项表达式，则可直接填入卡诺图,方法如下：
逻辑函数包含的最小项，其对应的方格填1。 逻辑函数不包含的最小项，其对应的方格填0。
用卡诺图表示3变量逻辑函数： F ABC ABC ABC ABC
所以：F F * * AC B D B F
不受变量数目的限制。
没有固定的步骤可循； 需要熟练运用各种公式和定理； 复杂的逻辑函数化简时需要技巧和经验； 有时很难判定化简结果是否最简。
1. 逻辑函数化简的意义和目标； 2. 逻辑函数的化简方法； 3. 公式法化简的方法和步骤。
逻辑函数的 卡诺图法化简
从真值表到卡诺图
已知某逻辑函数的真值表，用卡诺图表示该逻辑函数。
解 该函数有3个变量，先 画出3变量卡诺图，然 后根据真值表将8个最 小项的取值0或者1填入 卡诺图中对应的8个方 格中即可。
真值表
ABC L
000 0 001 0 010 0 011 1 100 0 101 1 110 1 111 1
A AC BD BEF （利用 A AB A ） A C BD BEF （利用 A AB A B ）
化简函数
F A A B A C B D A C E F B F D E F
逻辑函数及其化简

逻辑函数及其化简

第2章逻辑函数及其化简内容提要本章是数字逻辑电路的基础，主要内容包含：（1）基本逻辑概念，逻辑代数中的三种基本运算（与、或、非）及其复合运算（与非、或非、与或非、同或、异或等）。

（2）逻辑代数运算的基本规律（变量和常量的关系、交换律、结合律、分配律、重叠律、反演律、调换律等）。

（3）逻辑代数基本运算公式及三个规则（代入规则、反演规则和对偶规则）。

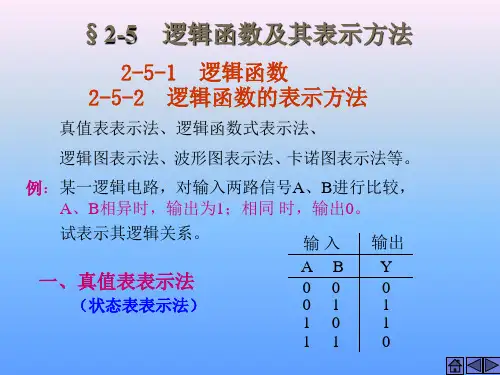
（4）逻辑函数的五种表示方法（真值表法、表达式法、卡诺图法、逻辑图法及硬件描述语言）及其之间关系。

本章主要讲述了前三种。

（5）逻辑函数的三种化简方法（公式化简法、卡诺图法和Q–M法）。

教学基本要求要求掌握：（1）逻辑代数的基本定律和定理。

（2）逻辑问题的描述方法。

（3）逻辑函数的化简方法。

重点与难点本章重点：（1）逻辑代数中的基本公式、基本定理和基本定律。

（2）常用公式。

（3）逻辑函数的真值表、表达式、卡诺图表示方法及其相互转换。

（4）最小项和最大项概念。

（5）逻辑函数公式化简法和卡诺图化简法。

主要教学内容2.1 逻辑代数中的三种基本运算和复合运算2.1.1 三种基本运算2.1.2 复合运算2.2 逻辑代数运算的基本规律2.3 逻辑代数的常用运算公式和三个规则2.3.1 逻辑代数的常用运算公式2.3.2 逻辑代数的三个规则2.4 逻辑函数及其描述方法2.4.1 逻辑函数2.4.2 逻辑函数及其描述方法2.4.3 逻辑函数的标准形式2.4.4 逻辑函数的同或、异或表达式2.5 逻辑函数化简2.5.1 公式法化简2.5.2 卡诺图化简2.1 逻辑代数中的三种基本运算和复合运算2.1.1 三种基本运算1. 与运算（逻辑乘）2. 或运算（逻辑加）3. 非运算（逻辑非）2.1.2 复合运算1. 与非运算与非运算是与运算和非运算的组合，先进行与运算，再进行非运算。

2. 或非运算或非运算是或运算和非运算的组合，先进行或运算，再进行非运算。

3. 与或非运算与或非运算是与运算、或运算和非运算的组合，先进行与运算，再进行或运算，最后进行非运算。

逻辑函数的化简及其门电路的实现

逻辑函数的化简及其门电路的实现

逻辑函数的化简 及其门电路的实
现
一、逻辑函数的化简法
（一）逻辑函数的公式化简法
（二）逻辑函数的卡诺图化简法
1.逻辑函数的最小项及最小项表达式
2.逻辑函数的卡诺图表示方法
1）卡诺图的画法规则的性质 2）用卡诺图化简逻辑函数的基本步骤
（三）含随意项的逻辑函数的化简
化简含随意项的逻辑函数时，充分利用随意项可以得到更加 简单的逻辑表达式，因而其相应的逻辑电路也更简单。在化简过 程中，随意项的取值可视具体情况取0或者取1。简单地说，如果 随意项对化简有利，则取1；如果随意项对化简不利，则取0。
二、逻辑函数门电路的实现
谢谢观看！
第三章逻辑函数及其化简

第三章逻辑函数及其化简


AB C ABC ABC
Y ( A, B, C ) m3 m6 m7 或： m (3,6,7)
最小项也可用“mi” 表示，下标“i”即最小项 的编号。编号方法：把最小项取值为1所对应的那 一组变量取值组合当成二进制数，与其相应的十进 制数，就是该最小项的编号。
三变量最小项的编号表
2、最小项表达式 任何一个逻辑函数都可以表示为最小项之和的 形式——标准与或表达式。而且这种形式是唯一的， 就是说一个逻辑函数只有一种最小项表达式。 例13 将Y=AB+BC展开成最小项表达式。 解： Y AB BC AB (C C ) ( A A) BC
或：
Y AB AB A
代入规则
2、吸收法 利用公式A+AB=A进行化简，消去多余项。 例6 化简函数 解：
Y A B A B CD( E F )
Y A B A B CD( E F ) AB
例7 化简函数
Y ABD C D ABC D( E F EF )
第四节
逻辑函数的卡诺图化简法
用代数法化简逻辑函数，需要依赖经验和技巧，有 些复杂函数还不容易求得最简形式。下面介绍的卡 诺图化简法，是一种更加系统并有统一规则可循的 逻辑函数化简法。 一、最小项及最小项表达式 1、最小项 设A、B、C是三个逻辑变量，若由这三个逻辑变 量按以下规则构成乘积项： ①每个乘积项都只含三个因子，且每个变量都是 它的一个因子； ②每个变量都以反变量(A、B、C)或以原变量(A、 B、C)的形式出现一次，且仅出现一次。
归纳简化任意逻辑函数的方法：
(1) A AB A （吸收法） AB AC BC AB AC (2) A AB A B （消去法） （3）AB AB A （并项法） （4）A A A A A 1 （配项法）
逻辑函数及其化简

逻辑函数及其化简


Y
≥1
按与-或式AB+C设计此逻辑电路，
& A BC
& & A B &
需两块芯片
二输入四或门74LS32一片
二输入四与门74LS10一片
按与非-与非式 AB· C 设计此逻辑电路，
只需要：二输入四与非门74LS00一片
C
常用的公式化简方法：
三、逻辑函数的公式化简法（自学）
利用基本公式和常用公式，再配合并项法、吸收法、配项法。
m1 m3 m2 m5 m7 m6
m2 m3 m6 m7 m4 m5
4、四变量全部最小项的卡诺图 Y= F（A、B、C、D）
Y CD AB 00 00 m0 01 11 01 11 10
YD 0 ABC 000 m0 001 011
1
10
m4 m12 m8
m1 m5 m13 m9
m3 m7 m15 m11
Y 0 1 1 0
所以： Y= AB + AB = m1 + m2 = （ m1 ， m2 ）
三、 逻辑图表示法
A 1
四、 波形图表示法
AB
≥1 Y
&
&
A
1
B
B
Y
AB
五、卡诺图表示法（在本章第七节中讲）
2-5-3
逻辑函数的两种标准形式
标准形式：最小项之和形式 、 最大项之积形式。 这里，重点介绍最小项之和形式。
0 0 1 1
0 1 0 1
m0 m1 m2 m3
3、四变量的全部最小项 编号为 m0~ m15 （略）
m0 m1 m2 m3 m4 m5 m6 m7
（二） 逻辑函数式表示法 在真值表中，将为“1”的输出 逻辑值所对应的输入变量的最小项相 加，即得对应的函数式。
逻辑函数的化简

逻辑函数的化简

1.3.4 逻辑函数的化简•对逻辑函数进行化简，可以求得最简逻辑表达式，也可以使实现逻辑函数的逻辑电路得以简化，这样既有利于节省元器件，也有利于提高可靠性。

•逻辑函数有如下三种化简方法：•公式化简法：利用逻辑代数的基本公式和规则来化简逻辑函数。

•图解化简法：又称卡诺图（Karnaugh Map）化简法。

•表格法：又称Q－M（Quine-McCluskey）化简法。

1.逻辑函数的公式化简法同一个逻辑函数，可以用不同类型的表达式表示，主要有以下五类：“与或”表达式、“或与”表达式、“与非”-“与非”表达式、“或非”-“或非”表达式、“与或非”表达式。

例如函数：=+Z AC AB“与或”表达式A B A C“或与”表达=++()()式AC AB“与非”-“与非”表达=⋅式=+++A B A C“或非”-“或非”表达式“与或非”表达式判断最简“与或”表达式的条件如下：(1)乘积项（即与项）个数最少的“与或”表达式；(2)当乘积项个数相等，则每个乘积项中因子（即变量）的个数最少的“与或”表达式。

例1-5 以下4个“与或”表达式是相等的，即它们表示同一个函数：(1)(2)(3)(4)=+++=++=++=++Z AC BC AB ACAC ABC ACAC BC ACAC AB AC 试判断哪一个是最简“与或”表达式。

(1)(2)(3)(4)=+++=++=++=++Z AC BC AB ACAC ABC ACAC BC ACAC AB AC 解：根据判断条件（1），式（1）含有4个与项，而式（2）～（4）都含有3个与项，因此，式（2）～（4）有可能最简；进一步比较与项中个数，式（3）和式（4）中，各与项都含2个变量，而式（2）中有一个与项含3个变量。

结论：式（3）和式（4）同为该函数的最简“与或”表达式。

公式法化简：借助定律和定理化简逻辑函数，常用以下几种方法。

(1)并项法利用互补率1A A +=()+=+=A BC A BC A B C C A B()()+++=⋅⊕+⋅⊕=A BC BC A BC BC A B C A B C A+=B ABD B，将两项合并为一项，合并时消去一个变量，如：(2)吸收法利用定理1（A + AB = A ），吸收掉（即除去）多余的项，如：(3)消去法利用定理2（+=+A AB A B ()++=++=+=+AB A C BC AB A B C AB ABC AB C(4)配项法根据互补律，利用()=+B A A B +A A ()()+++=+++++AB BC BC AB AB BC A A BC AB C C =+++++AB BC ABC A BC ABC ABC()()()=+++++AB ABC BC ABC A BC ABC =++AB BC A C），消去多余的因子，如：，先添上（）作配项用，以便最后消去更多的项。

逻辑函数及其简化


A + BC= A + B） A + C） （ （ ⋅
证明： 证明：右式 = A +AC +AB +BC = A（1+C+B）+BC （ ） = A+BC = 左式
A⋅ B + A⋅ B = A
证明： 证明： 左式 = A（B+B） （ ） = A = 右式
A + A⋅ B = A + B
右式=(A+B)(A+A) 右式 = A+AB+AA+AB =A+AB = 左式
A + A⋅B = A
A（1+B） 左式 = A（1+B）=A = 右式
A⋅B+A⋅C+B⋅C= A⋅B+A⋅C
左式= 左式 AB+AC+BC(A+A) = AB+AC+ABC+ABC = AB+AC = 右式
A⋅ B+ A⋅ C = A⋅ B+ A⋅ C
左式= 左式 AB AC =(A+B)(A+C) = AB+ A C + B C(A+A) = AB+ A C =右式 右式
+B
§10-1 逻辑函数的公式化简法 一、基本逻辑关系 3 非 逻辑运算 R us A F 与 或 非
条件 结果
日常事物中往往会有这种情况， 日常事物中往往会有这种情况，条件和
结果是一种相反的关系，这种条件 和 结果 的关系就是 非 逻辑关系 合上为“ 断开为“ 开关 A 合上为“1” 断开为“0” 逻辑变量 亮为“ 不亮为 不亮为“ 灯 F 亮为“1”不亮为“0” 逻辑函数 逻辑关系表达式： 逻辑关系表达式：F=

第3章逻辑函数运算规则及化简解读

【例3-10】将 F AB ABC 写成标准与或表达式。 。
解：F AB ABC AB(C C ) ABC ABC ABC ABC m 3,6,7
3.4.4 标准或与表达式
【例3-11】将 F ABC ABC ABC ABC 开为最大项之积的形式。
3.4.3 标准与或表达式
【例3-9】将
F ABC ABD
展开为最小项之和的形式。
解：F ABC ABD ABC ( D D) ABD(C C ) ABCD ABCD ABCD ABCD m15 m14 m6 m4 m 4, 6,14,15
3.2.4 逻辑代数的基本规则
1．代入规则 任何一个含有变量A的逻辑等式，如果将所有出现A的位置都 代之以同一个逻辑函数F，则等式仍然成立。 例: A（B+C）=AB+AC，等式中的C都用（C+D）代替， 该逻辑等式仍然成立，即 A（B+（C+D））=AB+A（C+D）
3.2.4 逻辑代数的基本规则
3.2.3 摩根定理
【例3-1】 应用摩根定理化简逻辑函数 解：反复应用摩根定理可得：
F ( AB C)( A BC)
F AB C A BC ABC ABC ( A B)C A( B C ) AC BC AB AC A BC
C
0 1 0 1 0 1 0 1
Y
0 0 0 1 0 1 1 1
3.3.4 卡诺图表述
(a) 2变量卡诺图
(b) 3变量卡诺图
(c) 4变量卡诺图
图3-2 2、3、4变量的卡诺图 CDE AB 00 01 11 10 000 m0 m8 m24 m16 001 m1 m9 m25 m17 011 m3 m11 m27 m19 010 m2 m10 m26 m18 110 m6 m14 m30 m22 111 m7 m15 m31 m23 101 m5 m13 m29 m21 100 m4 m12 m28 m20

逻辑函数的化简


逻辑相邻
根据逻辑相邻的定义,不难由图8-10看出, 几何相邻的两个方格的最小项满足逻辑相邻性. 而不直接相邻的方格,但以卡诺图中心轴对称 的方格对应的最小项也满足逻辑相邻,如图810c中m0与m2,m0与m8,m3与m11等,称这种相 邻叫对称相邻.所以卡诺图可看作是立体图. 这是卡诺图巧妙之所在 .
由图8-12中可以看出卡诺图覆盖过的变量以0 和1两种取值出现,则该变量被消去;只以0出 现,则该变量用反变量表示;只以1出现,则 以原变量出现.卡诺圈越大消去的变量越多, 能够合并相邻项的一个正确的卡诺圈必须符合 以下要求.
(1) 卡诺圈里的1方格数必须是2m个.m=0,1, 2,…. (2) 2m个1方格必须排列成方阵或矩阵. (3) 2m个1方格必须是方格相邻或对称相邻的.
二,公式化简
1.并项法 利用 A + A =1将两项合并成一 项并消去一个变量. 2.吸收法 3.消去法 F= = 利用A+AB=A,消去多余项. 利用A+AB=A+B,消去多余项.
AB + A B + A BD + ABD
AB + AB + D AB + A B
= AB + A B + D
4. 配项法
二,三,四个变量的函数的卡诺图
a.二变量函数的卡诺图 b.三变量函数的卡诺图. c.四变量函数的卡诺图
构造卡诺图时应遵循以下规则
① n变量函数有2n个最小项,则卡诺图有2n方 格,即方格与最小项一一对应. ② 2n个方格必须排列成方阵或矩阵. ③ 变量分成两组,行变量和列变量组,行变 量为高位组,列变量为低位组.如图8-10中C 中,为行变量,为列变量. ④ 变量取值遵守反射码的形成规则.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A
若开关接通为“ 1” 、 断开为“ 0” 灯亮为“ 1” 、 不亮为 “0”， 则图 11-1 所示关系的真值表如表 11.1 所示。 F＝A·B
R
＋UCC RC R1 F A R2 F A 1
表11.3 真值表 A F 0 1 1 0
E
S
EL
－UBB
(a)
(b)
(c)
图 11.3
（a） 非逻辑；（b） 三极管“非”门电路； （c） 非门逻辑符号
例11.1化简逻辑函数：
L AD AD AB AC BD ABEF BEF
L A AB AC BD ABEF BEF （利用 解：
A AC BD BEF
A A 1
）
（利用A+AB=A）
A C BD BEF
（利用 A AB A B）
A BC CB BD DB
（利用A+AB=A） （配项法）
A BC(D D) CB BD DB(C C)
A BCD BC D CB BD DBC DBC
A BC D CB BD DBC
（利用A+AB=A）
F AB AB AB C
解： F AB AB AB C
AB AB AB C AB ( A B)( A B)C AB ABC ABC
AB(C C) ABC ABC ABC ABC ABC ABC
逻辑代数的基本公式和定理
2.逻辑函数的公式化简法
1)逻辑函数式的常见形式
一个逻辑函数的表达式不是唯一的，可以有多种形式，并且能互相 转换。例如：
其中，与—或表达式是逻辑函数的最基本表达形式。
2)逻辑函数的最简“与—或表达式” 的标准
（1）与项最少，即表达式中“+”号最少。 （2）每个与项中的变量数最少，即表达式中“· ”号最少。
第3篇
11.1逻辑函数 1.基本逻辑关系 1）
数字电子技术
第11 章 逻辑函数及其化简
与逻辑是指当决定事件发生的所有条件A、B均具备时， 事件F才发生。如图 11-1 所示，只有当开关S1与S2同时接通 时灯泡才亮。 完整地表示输入输出之间逻辑关系的表格称为真值表。
若开关接通为“ 1” 、 断开为“ 0” 灯亮为“ 1” 、 不亮为 “0”， 则图 11-1 所示关系的真值表如表 11.1 所示。 F＝A·B
例11.2 化简逻辑函数： L AB AC BC CB BD DB ADE(F G)
解：L ABC BC CB BD DB ADE(F G) （利用反演律 ）
A BC CB BD DB ADE(F G)
（利用 A AB A B ）
L A AB BE A B BE A B E
（4）配项法
L AB AC BCD AB AC BCD( A A) AB AC ABCD ABCD AB AC
在化简逻辑函数时，要灵活运用上述方法，才能将 逻辑函数化为最简。 再举几个例子：
S1
S2
EL
Hale Waihona Puke 表11.1 真值表 A B F
0
0
0
1 0
0
0 0
E
1
1
1
1
图 11 –1 与逻辑举例
2）
或逻辑是指当决定事件发生的各种条件A、 B中只要具备 一个或一个以上时，事件 F 就发生。例如，把两个开关并联后 与一盏灯串联接到电源上，当两只开关中有一个或一个以上闭 合时灯均能亮，只有两个开关全断开时灯才不亮，如图11.2（a） 所示，真值表见表 11.2，其逻辑函数表达式为F＝A+B。
定的技巧和经验；有时很难判定化简结果是否最简。
11.2 逻辑函数的卡诺图化简法
一、 最小项的定义与性质
最小项的定义 n个变量的逻辑函数中，包含全部变量的乘积项称为最小项。n变 量逻辑函数的全部最小项共有2n个。
二、逻辑函数的最小项表达式 任何一个逻辑函数表达式都可以转换为一组最小项之和， 称为最小项表达式。
表 11.2 真值表 A 0 0 B 0 1 F 0 1
E S1 0 S2 EL 0 3V A 3V B V1 A V2 R －EC(－ 12 V) B ≥1 F
1
1
0
1
1
1
(a) (b)
(c)
图 11 .2 -(a) 或逻辑； (b) 二极管或门电路； (c) 或门逻辑符号
3）非逻辑
非逻辑是指某事件的发生取决于某个条件的否定，即某条 件成立，这事件不发生；某条件不成立， 这事件反而会发生。 如图 11. 3（a）所示，开关S接通，灯EL灭；开关断开。灯E L亮，灯亮与开关断合满足非逻辑关系。 其真值表见表 11.3， 其逻表达式为F= 。
A C D(B B) CB BD
A C D CB BD
（利用 A A 1）
例11.3 化简逻辑函数： L AB BC BC AB
解法1:
解法2：

由上例可知，逻辑函数的化简结果不是唯一的。
代数化简法的优点是不受变量数目的限制。 缺点是：没有固定的步骤可循；需要熟练运用各种公式 和定理；在化简一些较为复杂的逻辑函数时还需要一
例11.4：将以下逻辑函数转换成最小项表达式：
L( A, B, C ) AB AC
解：L( A, B, C) AB AC AB(C C) AC(B B)
ABC ABC ABC ABC =m7+m6+m3+m1
例11.5 将下列逻辑函数转换成最小项表达式：
3)用代数法化简逻辑函数
（1）并项法。
A A 1 运用公式
，将两项合并为一项，消去一个变量。如
L A(BC BC) A(BC BC) ABC ABC ABC ABC AB(C C) AB(C C)
AB AB A(B B) A
（2）吸收法。 运用吸收律 A+AB=A，消去多余的与项。如 L AB AB(C DE) AB （3）消去法。