当前位置：文档之家 › 第4章数据的统计描述

第4章数据的统计描述

  • 格式：pptx
  • 大小：840.13 KB
  • 文档页数：78

下载文档原格式

  / 78

合集下载

统计学第4章数据特征的描述

统计学第4章数据特征的描述

优缺点
极差计算简单，但容易受到极端值的影响，不能全面 反映数据的离散程度。
四分位差
定义
四分位差是第三四分位数与第 一四分位数之差，用于反映中
间50%数据的离散程度。
计算方法
四分位差 = 第三四分位数 第一四分位数
优缺点
四分位差能够避免极端值的影 响，更稳健地反映数据的离散
程度，但计算相对复杂。
方差与标准差
统计学第4章数据特征 的描述
https://
REPORTING
• 数据特征描述概述 • 集中趋势的度量 • 离散程度的度量 • 偏态与峰态的度量 • 数据特征描述在统计分析中的应用 • 数据特征描述的注意事项
目录
PART 01
数据特征描述概述
REPORTING
WENKU DESIGN
数据特征描述在推断性统计中的应用
参数估计 假设检验 方差分析 相关与回归分析
基于样本数据特征，对总体参数进行估计，如点估计和区间估 计。
通过比较样本数据与理论分布或两组样本数据之间的差异，对 总体分布或总体参数进行假设检验。
研究不同因素对总体变异的影响程度，通过比较不同组间的差 异，分析因素对总体变异的贡献。
定义
方差是每个数据与全体数据平均数之方根，用于衡量数据的波动大小。
计算方法
方差 = Σ(xi - x̄)² / n，标准差 = √方差
优缺点
方差和标准差能够全面反映数据的离散程度，且计算相对简单，但容易受到极端值的影响。同时，方差 和标准差都是基于均值的度量，对于非对称分布的数据可能不够准确。
适用范围
适用于数值型数据，且数据之间可能 存在极端异常值的情况。
特点
中位数不受极端值影响，对于存在极 端异常值的数据集，中位数能够更好 地反映数据的集中趋势。
spss第四章描述统计简介PPT课件

spss第四章描述统计简介PPT课件

定义：设，对样本数据集合中的所有数据的排序结果为X1≤X2≤…≤Xn，n为样本容 量，则上述排序的序列中，处于“正中间位置”上的数据，称为样本中位数。
当n 为奇数时：正中间位置号码=（n+1）/2 样本中位数=X(n+1)/2
当n为偶数时：正中间位置号码=（n+1）/2是小数，处于n/2与(n/2)+1之间。 样本中位数=(Xn/2+X(n/2)+1)/2 如5位同学的学习成绩：3，3，3，4，5。中间位置是第三位，中位数：3。 如果六位同学： 3，3，4，5，5，5。中间位置是3与4位中间的位置，中位数为： （4＋5）/2=4.5
第四章 描述统计量简介
2024/10/23
第三章 样本数据特征的初步分析
1
调查杭州市居民收入情况，得到
调查顾客对产品的满意第度情四况章， 获得100个样本数据，能分
样本100统个计样本量数描据，述根据这些数据，
析出哪些信息？
你最想得到哪些信息？
调查大学生群体中对手机品牌的偏 好程度，你如何描述调查结果？
• 选择Percentile Values 栏中的 选项，输出所选变量的百分值
• Dispersion（离差）栏，用于
指定输出反映变量离散程度的 统计量
• Central Tendency （集中趋势）
栏，用于指定输出反映变量集 中趋势的统计量
• Distribution （分布特征）栏，
用于指定输出描述分布形状和
如果样本容量为n，那么，某个样本值出现 的频率＝该样本值出现的频次/n
2024/10/23
第三章 样本数据特征的初步分析
9
分类数据或顺序数据描述频次与 频率的图形方法
《医学统计学》统计描述 (1)

《医学统计学》统计描述 (1)


2500 2500 2500 420
500 500 500
甲 乙丙
例4-9,etc
1.极差(Range） (全距)
符号：R 意义：反映全部变量值的
R X max X min
变动范围。
580
优点：简便,如说明传染病、
560 540
食物中毒的最长、最短潜 520
伏期等。
500
缺点：1. 只利用了两个 极端值
表2-2 115名正常成年女子血清转氨酶（mmol/L）含量分布
转氨酶含量
人数
12～
2
15～
9
18～
14
21～
23
24～
19
27～
14
30～
11
33～
9
36～
7
39～
4
42～45
3
人数
25
20 15
10 5
0
13.5 19.5 25.5 31.5 37.5 43.5. 血清转氨酶（mmol/L）
图2-2 115名正常成年女子血清转氨酶的频数分布
lg 表示以10为底的对数；
lg 1表示以10为底的反对数
X 0，为正值 （0，负数？）
几何均数的适用条件与实例
适用条件：呈倍数关系的等比资料或对数正态分 布（正偏态）资料；如抗体滴度资料
例 血清的抗体效价滴度的倒数分别为：10、
100、1000、10000、100000，求几何均数。
XG
lg1
图 2-3 101 名 正 常 人 血 清 肌 红 蛋 白 的 频 数 分 布
2. 描述计量资料的分布特征
①集中趋势(central tendency):变量值集中 位置。本例在组段“4.7~4.9”。
统计学原理第4章：数据特征的描述

统计学原理第4章：数据特征的描述


第四章 数据特征的描述
某公司400名职工平均工资计算表 单位:元
按月工资 组中值 职工
分组
x
人数
f
x f
比重(%)
f
f
①
②
③ ④=②×③ ⑤=③÷ 400
1100以下 1000
60
60000
15
1100-1300 1200 100 120000
25
1300-1500 1400 140 196000
35
分组
职工 人数
f
x f
①
1100以下 1100-1300 1300-1500 1500-1700 1700以上
②
1000 1200 1400 1600 1800
③ ④=②×③
60
60000
100 120000
140 196000
60
96000
40
72000
人数为权数
x x f f
544000 400
算术平均数、调和平均数、中位数、众数、几何平均数
3. 各种平均数的Excel操作
24/77
1. 集中趋势的含义
第四章 数据特征的描述
集中趋势是一组数据向其中心值靠
拢的倾向和程度
测度集中趋势就是寻找数据一般水
平的代表值或中心值
中心值 即：平均水平
▲
25/77
2. 集中趋势的度量方法
第四章 数据特征的描述
第四章 数据特征的描述
《统计学原理》（第3版）
第四章 数据特征的描述
学习目标
第一节 总量与相对量的测度 第二节 集中趋势的测度 第三节 离散程度的测度
2/77
第一节 总量与相对量的测度
社会统计学(第4章 数据的统计量描述)

社会统计学(第4章 数据的统计量描述)


三、离散性描述指标的比较
全距（四分位数） 全距（四分位数）
粗略、快捷，不稳定， 粗略、快捷，不稳定，不能用于有样本推论总体 用于定序、定距、 用于定序、定距、定比变量
标准差（方差） 标准差（方差）
精准、相对稳定， 精准、相对稳定，可以用于由样本推论总体 用于定距、 用于定距、定比变量
全距与标准差的关系
SS Σ(X − X ) 2 S = = N N
2
方差可以描述数值偏离平均值的程度。 方差可以描述数值偏离平均值的程度。 平方处理解决了绝对值的问题。 平方处理解决了绝对值的问题。 平方处理后对偏离均值的程度更加敏感。 平方处理后对偏离均值的程度更加敏感。
二、离散性的描述指标
4.标准差： 4.标准差：将方差开平方得到的数值 标准差
二、离散性的描述指标
5.分析下列4 5.分析下列4组数据的离散性 分析下列 6]、 a[6 6 6 6 6 6 6]、b[5 5 6 6 6 7 7 ] 9]、 c[3 3 4 6 8 9 9]、d[3 3 3 6 9 9 9 ]
全距=? 全距=? 四分位数=? 四分位数=? 平均离均差= 平均离均差=？ 方差=? 方差=? 标准差=? 标准差=?
三、集中性描述指标的比较
1.描述不同测量等级的变量 1.描述不同测量等级的变量
定类、定序、定距、 众 数：定类、定序、定距、定比变量的描述 中位数：定序、定距、 中位数：定序、定距、定比变量的描述 平均数：定距、 平均数：定距、定比变量的描述
三、集中性描述指标的比较
2.数据的分布形状 2.数据的分布形状 中心重合
第二节 集中性的描述指标
一、数据分布的集中性 二、集中性的描述指标 三、集中性描述指标的比较
一、数据分布的集中性
青岛版数学七年级上册第4章《数据的收集、整理与描述》教学设计

青岛版数学七年级上册第4章《数据的收集、整理与描述》教学设计

青岛版数学七年级上册第4章《数据的收集、整理与描述》教学设计一. 教材分析《青岛版数学七年级上册》第4章《数据的收集、整理与描述》的内容包括数据的收集、整理、描述和分析。

这部分内容是学生初步接触数据分析的基础知识，通过这部分的学习，使学生了解数据收集和整理的方法，学会用图表和统计量描述数据，并能对数据进行分析，从而培养学生对数据的敏感性和数据分析能力。

二. 学情分析七年级的学生已经具备了一定的逻辑思维能力和数学基础，但对于数据的收集、整理和描述可能还比较陌生。

因此，在教学过程中，需要引导学生从实际问题中提出数学问题，培养学生的数据意识，同时，要注重学生动手操作和小组合作的能力。

三. 教学目标1.了解数据的收集、整理和描述的方法；2.学会使用图表和统计量描述数据；3.能对数据进行分析，培养数据分析能力；4.培养学生的数据意识和团队协作能力。

四. 教学重难点1.数据的收集和整理方法；2.图表和统计量的表示方法；3.数据分析的方法和技巧。

五. 教学方法采用问题驱动法、案例教学法和小组合作法。

通过实际问题引导学生提出数学问题，培养学生的问题解决能力；通过案例教学，使学生了解数据的收集、整理和描述的方法；通过小组合作，培养学生的团队协作能力。

六. 教学准备1.教学PPT；2.教学案例和数据；3.小组合作学习资料。

七. 教学过程1.导入（5分钟）通过一个实际问题，引导学生提出数学问题，激发学生的学习兴趣。

例如：某班有50名学生，男生和女生各有多少人？2.呈现（15分钟）呈现教学案例和数据，让学生观察和分析数据，引导学生思考如何收集和整理数据。

例如：某班学生的身高数据如下：165, 170, 168, 162, 167, 172, 164, 166, 163, 169, 165, 171, 168, 160, 166, 170, 167, 164, 165, 162, 169, 166, 172, 163, 168, 164, 167, 165, 171, 166, 170, 162, 164, 167, 163, 169, 165, 172, 168, 166, 171, 167, 164, 165, 163, 168, 164, 167, 165, 171, 166, 170, 162, 164, 167, 163, 169, 165, 172, 168, 166, 171, 167, 164, 165, 163, 168, 164, 167, 165, 171, 166, 170, 162, 164, 167, 163, 169, 165, 172, 168, 166, 171, 167, 164, 165, 163, 168, 164, 167, 165, 171, 166, 170, 162, 164, 167, 163, 169, 165, 172, 168, 166, 171, 167, 164, 165, 163, 168, 164, 167, 165, 171, 166, 170, 162, 164, 167,在完成《青岛版数学七年级上册》第4章《数据的收集、整理与描述》的教学设计后，进行课堂反思是十分重要的。

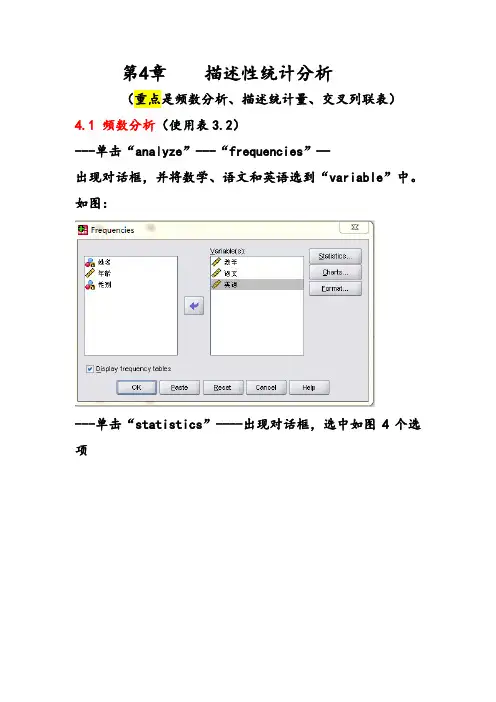
spss第四章,描述性统计分析。。

spss第四章,描述性统计分析。。

第4章描述性统计分析（重点是频数分析、描述统计量、交叉列联表）4.1 频数分析（使用表3.2）---单击“analyze”---“frequencies”—出现对话框，并将数学、语文和英语选到“variable”中。

如图：---单击“statistics”----出现对话框，选中如图4个选项-----单击“continue”回到前一对话框----单击“OK”结果如表4.1-----如图，重新选择语文---单击“charts”---得到一个对话框，如图选中2个选项----单击“continue”----回到前一对话框---单击“OK”。

结果如表4.24.2 基本描述统计量（使用表3.2）---单击“analyze”---“descriptive statistics”—“Descriptives”---得到对话框，并将数据进行如图选入：-----单击“options”—得到对话框，并选中如图6个选项：----单击“continue”----回到前一对话框---单击“OK”。

结果如表4.34.3 探索性分析（使用表3.2）---单击“analyze”---“descriptive statistics”—“Explore”---得到对话框，并将数据进行如图选入：----单击“Plots”—得到对话框，并选中如图4个选项：----单击“continue”----回到前一对话框---单击“OK”。

结果如表4.6（与书有不同）4.4交叉列联表分析（使用表化环0708）（1）T ransform（修改）----Recode into Different variable----选定身高------点击“向右箭头”------在“name”下写个名字：eg：T1-------change-------（此处T1和T2是已经做好的分组）点击-----old and new values对其分组---例：Range LOWEST through values :160 new values :1Rang :160 through :170 2Range HIGHEST through values :170 3 点击continue-----回到前一个对话框点击------OK同样的方法做好T2---------点击“analyze(分析)”-----“Descriptive Statistics(描述性统计)”------“Crosstabs（交叉列联表）”选中行列------点击“Exat….“则弹出“exct tests（精确检测）对话框”点“Statistics…”则弹出“Crosstabs：statistics（交叉表统计）对话框”-------点击“Chi—square（卡方检验）”----“continue”点“Cells…”则弹出“Crosstabs：Cells display（交叉表统计）对话框”-------选择“Counts”中的“Observed”和“Expected”为期望频数，-------选择“Percentages”中的“Row”“Column”“Total”选项，分别计算“频数”“列频数”“总频数”-------选择“Residuals”中的“Standardized”分别计算单元格的非标准化残差、标准化残差、调整后的残差----“continue”回到前一页点----“OK”4.5比率分析（课本71页）不需要掌握英语未写完作业：1-10，11-25，26-30。

《医学统计学》第四章定性资料的统计描述

《医学统计学》第四章定性资料的统计描述


1、不要把构成比与率相混淆。即分析时不能以构成 比代率；这是常见的错误。
某文章作者根据上述资料认为，沙眼在20～组的患病率最高，以后随年 龄增大而减少。该作者把构成比当作率进行分析，犯了以比代率的错误。
2、使用相对数时分母不宜过小。分母过小时相对数 不稳定。
3、注意资料的可比性；
不同时期、不同地区、不同条件下的资料比较时应注意具有 可比性。
12965.2
46.3
否
265
660291.4
40.1
说明该地市区非吸烟女性饮酒者的肺癌发病率是
非吸烟女性不饮酒者的1.15倍。
3.比数比
比数比（ Odds ratio ，OR） : 常用于流行病学
中病例-对照研究资料，表示病例组和对照组中的 暴露比例与非暴露比例的比值之比，是反映疾病 与暴露之间关联强度的指标。其计算公式为
一般的，两个地方的出生率、死亡率、发病率、不同级别 医院某病的治愈率等不能直接比较。
无可比性的实例：
由表2-7可见，无论有无腋下淋巴结转移，省医院的5年生存 率均高于市医院，但从总生存率看，省医院的5年生存率低于市 医院。这不符合常理。因此，省医院与市医院的总生存率就不能 直接比较（标准化后再比）。
感谢聆听
率
某事物或现象发生的实 际数 某事物或现象发生的所 有可能数
比例基数
公式中的“比例基数”通常依据习惯而定。
需要注意的是，率在更多情况下是一个具有时间 概念的指标，即用于说明在某一段时间内某现象 发生的强度或频率，如出生率、死亡率、发病率 、患病率等，这些指标通常是指在1年时间内发 生的频率。
例4-1 某单位在2009年有3128名职工，该单位 每年对职工进行体检，在这一年新发生高血压 病人12例，则
《统计学：思想、方法与应用》第4章 定量数据的描述方法

《统计学：思想、方法与应用》第4章 定量数据的描述方法


19:11
2
4.1 展示数据的分布
表4.1 安然公司1997-2001年股票价格变化的数据（单位：元）
一月
1998 0.78 1999 4.28
二月
0.62 4.34
三月
-0.69 2.44 -1.22 4.5
四月
-0.88 -0.28 0.47 4.56
五月
0.12 2.22
六月 七月 八月
0.75 0.81 -1.75 -0.5 2.06 -0.88 8
19:11
27
4.1.5 累积频数分布
除了对数据的分布形态有所了解，有时候我 们希望了解股价变化值低于0元的月份数量，累积 频数分布或累积频数折线图可以帮助我们获得这 样的信息。
股价变化值(元) -20~-10 频数 6 累积频数 6 由此得到
-10~0
0~10 10~20 20~30
19:11
1. 直方图：主要用于表示分组数据分布的一 种图形。 2. 用矩形的宽度和高度来表示频数分布 3. 在直角坐标中，用横轴表示数据分组，纵 轴表示频数或频率，各组与相应的频数就 形成了一个矩形，即直方图
本质上是用矩形的面积来
Excel
表示频数分布
19:11
19
4.1.2 分组数据看分布—直方图
（直方图与条形图的区别）
变量值变动区间的长度相等
异距分组 变量值变动区间的长度不完全相等
19:11
7
相关概念 组限
组距 组中值 指每组两端表示各组界限的变量值， 各组的最小值为下限，最大值为上限 每组变量值变动区间的长度，为上下 限之差
每组变量取值范围的中点数值
组中值=
19:11
统计学(第4章)

统计学(第4章)


连续变动结果的总量指标，时期指标是
一个流量。
时间维度上
时期指标的三个特点 具有可加性
时期指标可以累计
时期指标数值大小与时期长短有直接关系
时期指标的数值一般为连续登记
2019/6/15
第四章 描述统计
5
统计学
2、时点指标
时点指标又叫存量指标，是指反映社 会经济现象在某一时点上的总量指标，
四 季度
1 500
计划完成百分数=
1400+1420+1470+1500 5000
=115.8%
注：2010年第一季度前的四个季度的累计量已达5000，说明五年计 划提前三个季度完成。
2019/6/15
第四章 描述统计
33
统计学
（2）累计法
如何确定提前 完成时间？
计算公式：
计划完成相对指标 长期计划期间实际累计完成数 长期计划规定的累计数
时点指标是一个存量。
时间维度上
时点指标的三个特点
不具可加性
不同时点指标数值是不能累加
时点指标数值大小与时点间隔长短无直 接关系
时点指标一般为间断统计
2019/6/15
第四章 描述统计
6
统计学
三、总量指标的计量单位
1、实物量单位（包括度量衡单位） 2、价值量单位 3、劳动量单位（工时和工日）
5 000 1 250 1 340 1 280
102.4
52.4
4 000 1 000 1 030 1 215
121.5
56.1
2 000 500 600 400
80.0
50.0
11 000 2 750 2 970 2 895 105.33
4第四章 描述统计分析

4第四章 描述统计分析


第 四 章 描 述 统 计 分 析



第一节 第二节 第三节 第四节 第五节
频数分析 描述分析 探索分析 P-P图 SPSS表格处理：三线表的制作
第二节 描述分析


描述统计分析（Descriptives）过程是对变量进行 描述统计分析，包括计算集中趋势、离散趋势、分 布等统计指标，而且可将原始数据转换成标准Z分 值并存入数据集中。 所谓Z分值是指某原始数值比其均值高或低多少个 标准差，高时为正值，低时为负值，相等时为零。


spss230201684第四章描述统计分析第一章spss230简介与基本操作第二章数据编辑与整理第三章数据转换第四章描述统计分析第五章交叉表分析第六章比较平均值第七章方差分析第八章相关分析第九章回归分析第十章信度和效度分析第十一章非参数检验第十二章多选变量分析第十三章spss应用案例问卷调查分析第十四章spss应用案例测验质量分析第十五章探索性因子分析及案例应用第十六章基本统计图表的制作第十七章spss应用分析归纳小结从第四章开始讲解分析菜单命令下的数据分析方法点击分析菜单命令下拉子菜单



案例：【例4-4】试对某一次测验的测验分数对 该测验分数进行正态分布图形描述。 第1 步：打开分析数据。打开“测验数据文件 .sav”文件。 第2 步：启动分析过程。点击【分析】【描述统 计】【P-P图】】菜单，打开对话框。
第 3 步：设置分析变量。从左边的变量列表，通过单击向 右按钮可选择“总分”变量进入 “变量”（Variables） 列表框中。当然，可以同时选择多个变量，本例中仅选择 一个。

第 四 章 描 述 统 计 分 析
从第四章开始讲解【分析】菜单命令下的数 据分析方法，点击【分析】菜单命令下拉子 菜单。 包括：【报告】，【描述统计】，【定制表 】，【比较平均值】，【一般线性模型】， 【广义线性模型】，【混合模型】，【相关 】，【回归】，【对数线性】，【神经网络 】，【分类】，【降维】，【标度】，【非 参数检验】，【时间序列预测】，【生存分 析】，【多重响应】，【缺失值分析】，【 多重插补】，【复杂抽样】，【质量控制】 ，【ROC曲线图】，【时间和空间建模】。

医学统计人卫6版 第四章 定性数据的统计描述

第四章 定性数据的统计描述
.
一、定性数据的统计描述
➢定性数据的特点：将观察结果先按 分析要求，分类汇总观察单位数， 再用统计表列出。
➢常用相对比、构成比、率来描述计 数资料，这些指标统称为相对数。
.
二、常用相对数：
1.率（rate）： 表示某现象发生的频率和强度， 常以百分率（%）、千分率（‰）、万分率 （/万）、十万分率（/10万）等表示。
合计 16709 715 0
90 12.59
53.86 4.28
.
五、应用相对数时应注意的问题
1.根据要说明的问题，选择合适的相对数，不能 以构成比代替率；
2.计算时分母不宜过小，分母过小时相对数不稳 定。在观察例数较少时，应直接用绝对数表示， 以免引起误解。
3.对观察单位数不等的几个率，பைடு நூலகம்能直接相加求 其平均率即合计率（总率）不等于各分率（组 率）之和。
➢ 基本思想：采用统一的标准（人口构成、年龄 构成等）以消除混杂因素的影响。
例题1.2
.
标准化率的计算：直接法
已知某一影响因素标准构成的每层例数Ni或 已知标准构成的构成比时，选用该法。 标准构成可选：
另选一有代表性、较稳定、数量较大的 构成为标准；
取各层合计为标准； 在各组中任选一组作为标准构成。 P30例4-5；例4-6
4.资料的对比应注意可比性： 1）“同质”事物比较相对数才有意义； 2）其它影响因素在各组的内部构成是否相同，
若不同，应先进行标准化后再作比较。 5.率或比的比较，亦应考虑存在抽样误差，对于
样本之间的差异应作显著性检验。
.
.
小结
发病率、死亡率、病死率 率的标准化
.
计算公式为： 比 A B

医学统计学4. 定性数据的统计描述

计算题
已知健康男童体重近似服从正态分布，某年某地 150名12岁健康男童体重的均数为35kg，标准差为 6kg，试估计
1）该地12岁健康男童体重在50kg以上者占该地12岁健康男 童总数的百分比；
2）该地12岁健康男童体重30-40公斤占该地12岁健康男童的 百分比；
3）该地80%的12岁健康男童集中在哪个范围；
应用相对数的注意事项
例如，某医师对口腔门诊不同年龄龋齿患病情况 （表5-3）进行了分析，得出40~49岁组患病率高， 0~9岁组和70岁及以上组患病率低的错误结论。
年龄组（岁）
0~ 10~ 20~ 30~ 40~ 50~ 60~ 70~ 合计
表 5-3 口腔门诊龋齿患者年龄构成
患者人数
患者构成比（%）
一、统计学指标
绝对数：反应实际水平 相对数----两个数值的比，包括： 率 构成比 相对比
（一）率
率：
说明某现象或某事物在它可能发生的范围内实际发 生的频率或强度，又称频率指标或强度指标。
常以百分率（%）、千分率（‰）、万分率（1/ 万）、十万分率（1/10万）等表示，计算公式为：
率
某时期内实际发生某现象的观察单位数 同时期可能发生某现象的观察单位总数
比例基数
需要注意的是，分母中所规定的平均人口是指可 能会发生该病的人群。
2.患病率: 也称现患率，表示某一时点某人群人口 中患某病的频率，通常用来表示病程较长的慢性
病的发生或流行情况，其计算公式为
某病患病率
某地某时点某病患病例数 该地同期内平均人口数
比例基数
以上比例基数可为100%、1000‰、10000／万、 100000／10万，实际中患病率的分母通常为调查 的总人数，分子为患病的人数。

统计学第四章统计分析指标


计划完成相对指标
产值计划完成程度若大于100％，说明超额完 成计划；若小于100％，说明没有完成计划， 为正指标。 单位成本计划完成程度若大于100％，说明成 本比计划高，没有完成计划；若小于100％， 说明超额完成计划，为逆指标。 计划完成相对数的分子分母不能互换，在指 标含义、计算范围、核算方法等方面要一致。
计划完成相对指标
长期（通常是五年）计划完成情况—水平法和累计法
总体的一部分单位 总体另一部分单位 比例相对数
人口性别比例 积累与消费比例 农轻重比例
…
…
比例相对指标
人口出生性别比正常值一般在103到107之间。但 我国人口的出生性别比自20世纪80年代中期以来 迅速攀升。 1995年，0岁~4岁人口性别比：118.38 2000年，0岁~4岁人口性别比：120.17 2003年，0岁~4岁人口性6
（1）计划数为绝对数
计划完成相对数＝(实际完成数÷同期计划数)×100％
适用于研究分析社会经济现象的规模或水平的计划完成 程度。
计划完成相对指标
〔例〕 某公司2010年计划销售某种产品30万件， 实际销售32万件，则该公司2010年销售计划完成相对 指标是多少？超额完成计划多少？
销售计划完成相对指标 = （32/30）*100% = 106.7% 超额完成计划 = 106.7% - 100% = 6.7%
t1时段
t2时段
t3时段
时期指标的特点： 1. 不同时期的时期指标数值具有可加性； 2. 时期指标的数值大小与时期长短有直接关系； 3. 时期指标数值是连续登记、累计的结果。
时点指标的特点： 1. 不同时期的时点指标数值不具有可加性。 2. 时点指标的数值大小与时间间隔长短无关。 3. 时点指标的数值是间断计数的。

第四章 定量资料的统计描述(终板).

—
二、频数表的用途
1、揭示资料的分布特征和分布类型； 2、便于进一步计算指标和统计分析； 3、便于发现特大或特小的可疑值； 4、据此绘制频数分布图。
频数分布的特征
1、集中趋势：观察值向某一数值集中的 倾向（用平均数指标说明）；
2、离散趋势：观察值大小不等的倾向 （用变异指标说明）。
频数分布的类型
19695258999509901962582580505252595099019619625825805052525二选定适当的百分界值三决定正常参考值范围的单侧或双四选择正常参考值范围的估计方法一选择样本含量足够大的正常人25975059959599频数累计频数累计频率1260317208400766863613116014661341548194815119182128908231622895802723498323123598743523699163923810000合计238上表为某市238名健康人发汞含量求该市健康人发汞含量95正常值范围
第一节 频数表与频数图
• 一、定义： • 相同观察结果出现的次数称为频数（frequ
ency）。 • 将所有观察结果的频数按一定顺序排列在
一起，表达变量取值及其不同取值频数分 布情况的统计表称为频数分布表，简称频 数表（frequency table）。
二、频数分布表的编制
原始资料分组
按数量分组
n
n
• 故5个人抗体的平均滴度是1/70。
加权法：若相同观察值较多或资料已编制成频数
表则可利用加权法计算，其公式为：
G lg 1( f1 lg x1 f2 lg x2 ... fn lg xn ) lg 1( f lg X )
f1 f2 ... fn

统计学习题第四章数据分布特征的描述习题答案

第四章 静态指标分析法（一）一、填空题1、数据分布集中趋势的测度值（指标）主要有、和。

其中和用于测度品质数据集中趋势的分布特征，用于测度数值型数据集中趋势的分布特征。

2、标准差是反映的最主要指标（测度值）。

3、几何平均数是计算和的比较适用的一种方法。

4、当两组数据的平均数不等时，要比较其数据的差异程度大小，需要计算。

5、在测定数据分布特征时,如果M M e X 0==，则认为数据呈分布。

6、当一组工人的月平均工资悬殊较大时，用他们工资的比其算术平均数更能代表全部工人工资的总体水平。

二.选择题单选题：1.反映的时间状况不同，总量指标可分为（ ）A 总量指标和时点总量指标B 时点总量指标和时期总量指标C 时期总量指标和时间指标D 实物量指标和价值量指标2、某厂1999年完成产值200万元，2000年计划增长10%，实际完成了231万元，超额完成( )A 5.5%B 5%C 115.5%D 15.5%3、在同一变量数列中，当标志值（变量值）比较大的次数较多时，计算出来的平均数（ ）A 接近标志值小的一方B 接近标志值大的一方C 接近次数少的一方D 接近哪一方无法判断4、在计算平均数时，权数的意义和作用是不变的，而权数的具体表现（ ）A 可变的B 总是各组单位数C 总是各组标志总量D 总是各组标志值 5、1998年某厂甲车间工人的月平均工资为520元，乙车间工人的月平均工资为540元，1999年各车间的工资水平不变，但甲车间的工人占全部工人的比重由原来的40%提高到了60%，则1999年两车间工人的总平均工资比1998年（ ）A 提高B 不变C 降低D 不能做结论 6、在变异指标（离散程度测度值）中，其数值越小，则（ ）A 说明变量值越分散，平均数代表性越低B 说明变量值越集中，平均数代表性越高C 说明变量值越分散，平均数代表性越高D 说明变量值越集中，平均数代表性越低7、有甲、乙两数列,已知甲数列:07.7,70==甲甲σX ;乙数列:41.3,7==乙乙σX 根据以上资料可直接判断( )A 甲数列的平均数代表性大B 乙数列的平均数代表性大C 两数列的平均数代表性相同D 不能直接判别8、杭州地区每百人手机拥有量为90部，这个指标是 （ ）A 、比例相对指标B 、比较相对指标C 、结构相对指标D 、强度相对指标 9、某组数据呈正态分布，计算出算术平均数为5，中位数为7，则该数据分布为 （ ） A 、左偏分布 B 、右偏分布 C 、对称分布 D 、无法判断10、加权算术平均数的大小 （ ）A 主要受各组标志值大小的影响，与各组次数多少无关；B 主要受各组次数多少的影响，与各组标志值大小无关；C 既与各组标志值大小无关，也与各组次数多少无关；D 既与各组标志值大小有关，也受各组次数多少的影响11、已知一分配数列，最小组限为30元，最大组限为200元，不可能是平均数的为 （ ） A 、50元 B 、80元 C 、120元 D 、210元12、比较两个单位的资料，甲的标准差小于乙的标准差，则 （ ） A 两个单位的平均数代表性相同 B 甲单位平均数代表性大于乙单位C 乙单位平均数代表性大于甲单位D 不能确定哪个单位的平均数代表性大 13、若单项数列的所有标志值都增加常数9，而次数都减少三分之一，则其算术平均数 （ ） A 、增加9 B 、增加6C 、减少三分之一 D 、增加三分之二 14、如果数据分布很不均匀,则应编制( )A 开口组B 闭口组C 等距数列D 异距数列 15、计算总量指标的基本原则是：( ) A 总体性B 全面性C 同质性D 可比性16、某企业的职工工资分为四组:800元以下;800-1000元;1000—1500元;1500以上,则1500元以上这组组中值应近似为()A1500元 B 1600元 C 1750元D 2000元 17、统计分组的首要问题是( )A 选择分组变量和确定组限B 按品质标志分组C 运用多个标志进行分组,形成一个分组体系D 善于运用复合分组18、某连续变量数列,其末组为开口组,下限为200,又知其邻组的组中值为170,则末组组中值为( )A 230B 260C 185D 215 19、分配数列中,靠近中间的变量值分布的次数少,靠近两端的变量值分布的次数多,这种分布的类型是( )A 钟型分布B U 型分布C J 型分布D 倒J 型分布 20、要了解上海市居民家庭的开支情况，最合适的调查方式是：（） A 普查B 抽样调查C 典型调查D 重点调查21、已知两个同类企业的职工平均工资的标准差分别为5元和6元,而平均工资分别为3000元，3500元则两企业的工资离散程度为 ( )A 甲大于乙B 乙大于甲C 一样的D 无法判断 22、加权算术平均数的大小取决于( )A 变量值B 频数C 变量值和频数D 频率23、如果所有标志值的频数都减少为原来的1/5,而标志值仍然不变.那么算术平均数( ) A 不变 B 扩大到5倍 C 减少为原来的1/5 D 不能预测其变化 24、 计算平均比率最好用 ( )A 算术平均数B 调和平均数C 几何平均数D 中位数25、若两数列的标准差相等而平均数不同,在比较两数列的离散程度大小时,应采用() A 全距 B 平均差 C 标准差 D 标准差系数26、若n=20,∑∑==2080,2002x x ,标准差为( )A 2B 4C 1.5D 327、已知某总体3215,3256==eMM,则数据的分布形态为( )A左偏分布B正态分布 C 右偏分布DU型分布28、一次小型出口商品洽谈会,所有厂商的平均成交额的方差为156.25万元，标准差系数为14.2%,则平均成交额为( )万元A11 B 177.5 C 22.19 D 8826、欲粗略了解我国钢铁生产的基本情况，调查了上钢、鞍钢等十几个大型的钢铁企业，这是（）A普查B重点调查C典型调查D抽样调查多选题：1.某企业计划2000年成本降低率为8%，实际降低了10%。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


正态分布：在自然现象和社会现象中，大量的随机变量都 服从戒近似服从正态分布，也叫高斯分布。

正态分布的特征：

正态分布曲线是一条对称曲线，关于均数对称； 曲线是单峰，在均值处达到最高点； 正态分布曲线的矮阔与尖峭与标准差有关。标准差越大， 个体差异越大，正态曲线也越矮阔；反之，标准差越小， 个体差异越小，正态曲线也越尖峭。 曲线无论向左或向右延伸，都越来越接近横轴，但不会与 横轴相交，以横轴为渐近线。

标准正态分布即将原始数据进行标准化变换，也被称为Z 分布。 X X
Z



通过标准化可得到一系列的变量值，通常称为标准化值， 或Z分数。 标准化值反映的是变量值与变量均值的差是几个标准差单 位。如果标准化值等于0，则表明该变量值等于变量均值； 如果标准化值大于0，则表明该变量值大于变量均值；如 果标准化值小于0，则表明该变量值小于变量均值； 将数据标准化后分为三组：Z≤-3，-3＜Z ＜3，Z≥3 如果数据在第一组或第三组的比例大于理论值0.3%，则可 认为存在异常值。

中位数（Median）是将总体各单位的标志值按大小顺序 排列，处亍中间位置的那个标志值。剩下的值一半比它大， 一半比它小。 设标志值X 1 X 2 X 3 X n
则中位数M ＝X ( n 1) / 2 当n为奇数时 M ＝( X n / 2 X n / 21 ) / 2 当n为偶数时
正偏或右偏分布
中均数 众数位数
三值合一
对称分布
X
中位数 均数众数
负偏或左偏分布

由亍均数较易受极端值的影响，因此可以考虑将数据排序
后，按一定比例去掉两端的数据，只使用中部的数据来求均数， 即截尾均数。

如果截尾均数和原均数相差不大，则说明数据不存在极端
值，或者两侧极端值的影响正好抵消；反之，则说明数据中有
各种统计描述指标：均数、标准差、四分位数间距、百分 比等；
统计表：将统计指标组成表格，可同时呈现多种统计指标， 并进行复杂的样本分组、合并计算； 统计图：按照统计指标的大小将其绘制成一张图形，对于 连续变量数据，常用直方图、箱图加以展示，对于分类变 量，常用条图、饼图加以展示。


变量的类型
Nominal变量 （名义型）

X
n
i
均数的最重要意义在于它高度浓缩了数据，使大量的观测
数据变为一个代表性数值。但它掩盖了各个观测数据之间 的差异性，且对极端值比较灵敏，在某些情况下也有一定
欺骗性。
均数适用范围： 单峰和基本对称的分布情况下适用于描述集中趋势。 严格讲均数只适用于定距变量，但有时对于定序变量，求 平均等级也可使用均数。
布范围。
R X max X min

斱差：即平均了每个数据的离均差的平斱值。可用亍丌同 含量样本数据分布离散程度的比较。

方差越大，数据分布的离散程度越大。

标准差：将斱差开斱得到标准差。标准差度量了偏离平均 数的大小，相当亍平均偏差，可直接地、概括地、平均地
描述数据变异的大小。

标准差越小，表明数据越整齐，变异程度越小。标准差越 大，表明数据分布越分散，变异程度越大。
确定是否在结果中 输出频数表。连续 变量通常不输出频 数表。
可同时选入多 个需要描述的 变量，系统依 次进行分析

II. 使用Frequencies过程计算统计量（Statistics）幵绘制直斱图 （Charts选项卡）。
百分点数值选 项组 按某一数值等 分 集中趋势选 项组
输入给定位置 的百分点

Descriptives过程通常用亍输出连续变量的基本描述统计 量。

主要功能：

只可用于连续变量。 计算各种基本统计量，但与Frequencies相比，不可计算分 位数、中位数、众数等。 重要功能在于将数据标准化。


Explorer过程可用亍输出将变量分类后的连续变量的基本 描述统计量。

中位数是位置平均数，因此不受极端值的影响。
中位数适用范围： 非基本对称的分布情况下可使用于中位数描述集中趋势。 中位数对于定序变量、连续变量都可以使用。 中位数只考虑居中位置，因此用于描述连续变量会损失很 多信息。所以对于对称分布的资料，往往优先考虑均数。

众数（Mode）是样本数据中出现频次最大的那个数字。

异常值的判断


Frequencies过程即频数分析，是最基本的数据分析过程。 主要功能：

既可用于连续变量，也可用于分类变量 生成频数表 计算各种基本统计量，可计算百分位数 对于连续变量可绘制带正态曲线的直方图 对于分类变量可绘制饼图、条图等

针对数据“住房状况调查”
百分位数（Percentile）是一种位置指标，用Px表示。一个 百分位数将一组观察值分为两部分，理论位置有x%的观察值

比它小，(100－x)%的观察值比它大。
四分位数即三个数据的总称，分别是P25、P50和P75分位数。 这三个分位数将全部总体单位按标志值的大小等分为四部分。

分别记为Q1、Q2和Q3。
极端值，此时截尾均数能更好地反映数据的集中趋势。

常用的截尾均数有5%截尾均数，即两端各去掉5%的数。

离散趋势是指一组数据远离其中心值的程度，是关亍数据 波动范围的描述。

在统计学中，关亍数据离散趋势的统计量被称为尺度统计 量（Scale Statistic）。
常用的尺度统计量有：


全距——适用于所有分布类型的资料 标准差、方差——适用于正态分布资料

IV. （1）取消数据拆分，使用Descriptives过程将数据标准化。
将标准化后的变量 值作为一个新变量 保存在数据集中。

（2）将标准化后的Z值进行排序（Sort Cases），看是否存在 绝对值大亍3的Z值，即为异常值。 （3）用Recode命令将Z值分组，计算异常值组的百分比，不 理论值0.3%相比较判断是否存在丌均衡现象。
Ordinal变量 （定序型）
Scale变量 （定 距定比型）
分类变量
可视作分类变量， 也可处理后视作 连续变量
连续变量
5

集中趋势是指一组数据向某一中心值靠拢的倾向，是关亍 中心位置的描述。

在统计学中，关亍数据分布的中心位置的统计量被称为位 置统计量（Location Statistic）。
四分位数间距——适用于所有分布类型的资料

全距又称为极差，是一组数据中最大值（Maximum）不
最小值（Minimum）之差.

极差衡量的是变量分布的变异范围或离散幅度。 它仅仅取决于两个极端值的水平，不能反映其间的变量分
布。

它容易受个别极端值的影响，并不稳定。

全距一般只用亍预备性检查，目的是大体上了解数据的分

四分位数间距即（Q3 —Q1）
四分位数间距（ Q3 － Q1 ）的适用范围： 四分位数间距包括了中间50%的观察值，因此既排除了两 端极端值的影响，又能够反映较多数据的离散程度，是当方 差、标准差不适用时较好的离散程度描述指标。
四分位数间距越大表明中间的数据越分散，越小表明中间 的数据越集中，在描述数据的离散程度上比极差的稳定性要 高。
选入按某种 因素分组的 分类变量
输出描述性 统计量，指 定置信区间
箱图
茎叶图
极端值，输 出5个最大 值，5个最 小值。
输出5%、 10%、25%、 50%、75%、 95%分位数
I. II. 分析户主的“从业情况”和“房屋产权情况 ”，绘制频数
表和条图
针对“家庭收入”和“现住面积”计算均数、标准差、中 位数以及P5、P95，并绘制带正态曲线的直方图 ；
III. 比较本地户口和外地户口的人均住房面积 情况。
IV. 分析人均住房面积是否存在不均衡现象。

I. 使用Frequencies过程绘制频数表和条图（Charts选项卡）。

数据的分布形态主要指数据分布是否对称，偏斜程度如何， 分布陡缓程度等。

在统计学中，关亍数据分布形态的统计量被称为分布统计 量（Distribution Statistic）。
常用的分布统计量有：


偏度系数 峰度系数

偏度系数是描述变量取值分布形态对称性的统计量。

当分布为对称分布时，正负总偏差相等，偏度值等于0；当
常用的位置统计量有：


均数——适用于正态分布和对称分布资料； 中位数——适用于所有分布类型的资料。
众数——适用于所有分布类型的资料。

算术均数（Arithmetic Mean）是最常用的描述数据分布的 集中趋势的统计量。总体均数用μ表示，样本均数用X表示。
X X 2 … X n X 1 n
第4章
4.１ 连续变量的统计描述
4.２ 分类变量的统计描述 4.３ 多选题的统计描述 4.4 统计图的呈现

描述性统计分析：用少量数字（即描述指标）概括大量原 始数字，对数据进行描述；


推断性统计分析：从样本信息回推总体特征。
统计描述中可用的工具

各种初步汇总描述方法：分组汇总、百分位数刻画


众数不受极端值影响，但对资料的使用不完全，使用众数 反映连续变量会损失很多信息。
当数据为对称分布戒接近对称分布时： 应选择均值作为集中趋势的代表值，因为此时均值不众 数和中位数的差异很小，而又是全部数据的综合，因此具有 很好的代表性。 当数据为偏斜度较大的非对称分布时： 均值此时受极端值的影响，而偏离数据的集中点；此时应 选择众数和中位数来代表。