加减法的数字谜
- 格式:ppt
- 大小:201.00 KB
- 文档页数:16
《数学》教案教材版本:实验版 . 学校: .第一课时复备内容及讨论记录教学过程一、导入师:我们生活的地球非常的神奇,除了我们生活的陆地之外,还有更广袤的大海,,经过了几千年沧海桑田的变化,有很多古城都沉没在了大海之中,海底的奥秘也等着我们去探索去发现。
我们今天就随着卡卡它们一起来看看海底都存在哪些奥秘吧!(播放动画导入)二、呈现问题(一)呈现问题1师:据说当时这里的人们主要以海盗为业,因此警惕性和防备性都很高。
卡卡它们刚接近海盗之都,就发现这里到处都设有密码和机关。
看来想探秘这座海底之城,并不是件容易的事。
例1:在下面洞内,填上适当的数字,使算式成立。
1、学生读题,收集信息,先独立思考。
2、师生合作探究。
师:看完这几个数字谜,你发现了什么?突破口在哪呢?生:突破口在最低位,也就是个位。
师:计算加法竖式时,一定要注意连续进位;计算减法竖式时,一定要注意连续退位。
(注意有些题目有多个答案,书写完整)3、学生独立完成。
(找学生板书,教师点评,指出不足以及书写不规范的地方)答案:4、总结交流。
师:寻找突破口,对式子进行简单的推理,这就是咱们今天要学的内容。
揭示课题板书——加减法数字谜(二)大胆闯关11、(1)在下面算式的□里填上适当的数字,使算式成立。
(2)下面加法算式中,相同的汉字代表相同的数字,当每个汉字代表什么数时,竖式成立?(1)学生读题,收集信息,先独立思考。
(2)本题较简单,教师适当的提示。
师:本题的突破口在个位,出现这个图形或字母或文字能代表几个数字时,要逐个检验哪个数字或哪几个数字是符合题意的。
(3)学生独立完成答案:(4)总结交流。
师:寻找突破口,验证每个答案,不要多写,也不要漏写。
(三)呈现问题2师:卡卡、罗拉和豆丁经过简单的分析,很快就从门前捡起数字石块塞进洞内,三个城门打开的顷刻间,卷起了海底的污泥。
混沌中,它们来到一个离它们最近的建筑物旁,据说这就是当时海盗们的交易市场,而且只有答对门上题目的人才有资格进去!你能答对吗?例2:在方框内填上适当的数字,使算式成立。

数字谜从形式上可以分为横式数字谜与竖式数字谜,从运算法则上可以分为加减乘除四种形式的数字谜。
横式与竖式亦可以互相转换,本讲中将主要介绍数字谜的一般解题技巧。
主要涉及小数、分数、循环小数的数字谜问题,因此,会需要利用数论的知识解决数字谜问题一、数字迷加减法1.个位数字分析法2.加减法中的进位与退位3.奇偶性分析法二、数字谜问题解题技巧1.解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;2.要根据不同的情况逐步缩小范围,并进行适当的估算;3.题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性;4.注意结合进位及退位来考虑;模块一、加法数字谜【例 1】 “华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?0191杯华24+【考点】加法数字谜 【难度】1星 【题型】填空 【关键词】华杯赛,初赛,第1题 【解析】 由0+“杯”=4,知“杯”代表4(不进位加法);再由191+“华”=200,知“华”代表9.因此,“华杯”代表的两位数是94.【答案】94【例 2】 下面的算式里,四个小纸片各盖住了一个数字。
被盖住的四个数字的总和是多少?例题精讲知识点拨教学目标5-1-2-1.加减法数字谜1+49【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】华杯赛,初赛,第5题 【解析】 149的个位数是9,说明两个个位数相加没有进位,因此,9是两个个位数的和,14是两个十位数的和。
于是,四个数字的总和是14+9=23。
【答案】23【例 3】 在下边的算式中,被加数的数字和是和数的数字和的三倍。
问:被加数至少是多少?【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】第四届,华杯赛,初赛,第2题 【解析】 从“被加数的数字和是和的数字和的三倍”这句话,可以推断出两点:①被加数可以被3整除。

数字谜从形式上可以分为横式数字谜与竖式数字谜,从运算法则上可以分为加减乘除四种形式的数字谜。
横式与竖式亦可以互相转换,本讲中将主要介绍数字谜的一般解题技巧。
主要涉及小数、分数、循环小数的数字谜问题,因此,会需要利用数论的知识解决数字谜问题一、数字迷加减法1.个位数字分析法2.加减法中的进位与退位3.奇偶性分析法二、数字谜问题解题技巧1.解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;2.要根据不同的情况逐步缩小范围,并进行适当的估算;3.题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性;4.注意结合进位及退位来考虑;模块一、加法数字谜【例 1】 “华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?例题精讲知识点拨教学目标5-1-2-1.加减法数字谜0191杯华24+【考点】加法数字谜 【难度】1星 【题型】填空 【关键词】华杯赛,初赛,第1题【解析】 由0+“杯”=4,知“杯”代表4(不进位加法);再由191+“华”=200,知“华”代表9.因此,“华杯”代表的两位数是94.【答案】94【例 2】 下面的算式里,四个小纸片各盖住了一个数字。
被盖住的四个数字的总和是多少?1+49【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】华杯赛,初赛,第5题【解析】 149的个位数是9,说明两个个位数相加没有进位,因此,9是两个个位数的和,14是两个十位数的和。
于是,四个数字的总和是14+9=23。
【答案】23【例 3】 在下边的算式中,被加数的数字和是和数的数字和的三倍。
问:被加数至少是多少?【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】第四届,华杯赛,初赛,第2题【解析】 从“被加数的数字和是和的数字和的三倍”这句话,可以推断出两点:①被加数可以被3整除。


三年级思维拓展之加减法数字谜1.在下列各竖式的□中填上适当的数字,使竖式成立2.在下列各竖式的□中填上适当的数字,使竖式成立3.下面算式中的数字都被遮盖住了,求竖式中被遮盖住的几个数字的和。
4..如图,算式中相同的汉字代表相同的数字,不同的汉字代表不同的数字,那么“玩中学”代表的三位数是.5.如图,在竖式的每个方框中填入一个数字,要求所填的数字都是质数,使得竖式成立。
6.下面算式中的每个汉字都代表一个数字,不同的汉字代表不同的数字。
当它们各代表什么数字时算式成立?7.算下面竖式中的汉字各代表多少?8.求当它们各代表什么数字时,能够使算式成立?9.请你猜一猜,每个算式中的汉字各表示几?10.相同的英文字母代表相同的数字,你知道下面A、B、C代表几?参考答案【解答】加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是92.【解答】这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
3.【解答】这是一道三个三位数的加法。
从和的前两位是29,可断定三个加数的百位必须是9,因为三个9的和才是27,多出的部分便是进位造成的。
同理,可断定加数的三个十位数字的和,也必须是9,多出的2(29-27),是个位进位造成的。
而和的个位数是1,断定三个加数的个位数字和是21。
因此,被遮盖的数,数字和是:27+27+21=754.【答案】465【解答】从加法的十位运算可以看出“啊”=0。
因为显然“玩”和“学”都不能是0,所以其中一定有一个是5。

第9章加减法数字谜数字谜,指的是在某些算式中,含有一些用符号、汉字、字母表示的待定数字,要求出待定数字使算式成立。
数字谜的特点是,一个符号、汉字或字母表示一个数字,不同的符号、汉字或字母表示不同的数字。
在算式成立的前提下,求出每个符号、汉字、字母各自代表的数字。
破字谜的分析思考方法与竖式填空格的分析思考方法基本相同,也就是审题、选择解题突破口、确定各符号、汉字或字母所代表的数字这三个步骤。
在第三个步骤中,同样需要根据已知数字的关系与特征,确定要填数字的大致范围,然后进行分类讨论,以确定各符号、汉字或字母所代表的数字。
例1. 在下面的加法算式中,“东”、“湖”、“水”、“磨”、“山”“梅”、“美”、“在”、“江”、“城”这十个汉字分别表示0~9这十个数字,其中“水”表示9,“磨”表示2,“山”表示8,问“美在江城”所表示的四位数是多少?东湖水+磨山梅美在江城分析与解观察算式可以发现,这道算式是两个三位数相加,相加的和是四位数。
根据加法的计算法则容易确定和的千位上的数字,所以选择“美”字作为突破口。
由于“东”和“磨”相加,最多向前一位进1,所以“美”表示1。
由于“磨”表示2,即“东”加上2的和是两位数1在,又由于算式中没有相同的数字,所以“东”表示7,“在”表示0,且“湖”加上“山”的和要向百位进1。
由于“水”有示9,“山”表示8,这时“湖”、“梅”、“江”、“城”这四个汉字只能分别表示3,4,5,6这四个数字中的一个。
显然“梅”不能表示3,若“梅”表示4,则“城”表示3,“湖”表示6,“江”表示5;若“梅“表示5,则“城”表示4,那么“湖”和“江”就不能满足题目的要求,所以“梅”不能表示5;若“梅”表示6,则“城”表示5,“湖”表示4,“江”表示3。
因此,美在江城可以表示的四位数有两个1053或1035。
评注在数字谜的分析解答过程中常常要进行尝试,为了减少尝试的次数,可以通过对某些数位上的数作些合理的估算,以缩小所求数字的取值范围。

一、加减法数字谜分析方法(1)个位数字分析法(2)加减法中的进位与错位(3)奇偶性分析法 二、乘除法数字迷分析方法数字乘法个位数字的规律→最大值最小值的考量→加减法进位规律→合数分解质因数性质→奇偶数性质规律→余数性质。
三、数字谜问题解题技巧(1)解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;(2)要根据不同的情况逐步缩小范围,并进行适当的估算;(3)题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性; (4)注意结合进位及退位来考虑;(5)有时可运用到数论中的分解质因数等方法。
【例题1】下图是一个正确的加法算式,其中相同的字母代表相同的数字,不同的字母代表不同的数字.已知BAD 不是3的倍数,GOOD 不是8的倍数,那么ABGD 代表的四位数是多少?BA D BA D GO O D + 【考点】加法数字谜【难度】【解析】首先可以确定D 的值一定是0,G 的值一定是1,所以GOO BA BA =+,可见GOO 为偶数,只能是122、144、166、188,由于BAD 不是3的倍数,GOOD 不是8的倍数,所以GOO 不是3的倍数,也知识点拨例题精讲不是4的倍数,可以排除144和188,再检验122和166可知只有166符合,此时BAD为830,所以ABGD 的值为3810。
【例题2】“迎杯×春杯=好好好”在上面的乘法算式中,不同的汉字表示不同的数字,相同的汉字表示相同的数字。
那么“迎+春+杯+好”之和等于多少?【考点】乘法数字谜【难度】【解析】好好好=好×111=好×3×37,100以内37的倍数只有37和74,所以“迎杯”或“春杯”中必有1个是37或74,判断出“杯”是7或4。
若杯=7,则好=9,999/37=27,所以,迎+春+杯+好=3+2+7+9=21。
若杯=4,则好=6,666/74=9,不是两位数,不符合题意。


5-1-2-1.加減法數字謎教學目標數字謎從形式上可以分為橫式數字謎與豎式數字謎,從運算法則上可以分為加減乘除四種形式的數字謎。
橫式與豎式亦可以互相轉換,本講中將主要介紹數字謎的一般解題技巧。
主要涉及小數、分數、循環小數的數字謎問題,因此,會需要利用數論的知識解決數字謎問題知識點撥一、數字迷加減法1.個位數字分析法2.加減法中的進位與退位3.奇偶性分析法二、數字謎問題解題技巧1.解題的突破口多在於豎式或橫式中的特殊之處,例如首位、個位以及位數的差異;2.要根據不同的情況逐步縮小範圍,並進行適當的估算;3.題目中涉及多個字母或漢字時,要注意用不同符號表示不同數字這一條件來排除若干可能性;4.注意結合進位及退位來考慮;模組一、加法數字謎【例 1】 “華杯賽”是為了紀念和學習我國傑出的數學家華羅庚教授而舉辦的全國性大型少年數學競賽.華羅庚教授生於1910年,現在用“華杯”代表一個兩位數.已知1910與“華杯”之和等於2004,那麼“華杯”代表的兩位數是多少?0191杯华2040+【考點】加法數字謎 【難度】1星 【題型】填空【關鍵字】華杯賽,初賽,第1題【解析】 由0+“杯”=4,知“杯”代表4(不進位加法);再由191+“華”=200,知“華”代表9.因此,“華杯”代表的兩位數是94.【答案】94【例 2】 下麵的算式裏,四個小紙片各蓋住了一個數字。
被蓋住的四個數字的總和是多少?1+49【考點】加法數字謎 【難度】2星 【題型】填空【關鍵字】華杯賽,初賽,第5題【解析】 149的個位數是9,說明兩個個位數相加沒有進位,因此,9是兩個個位數的和,14是兩個十位數的和。
於是,四個數字的總和是14+9=23。
【答案】23【例 3】 在下邊的算式中,被加數的數字和是和數的數字和的三倍。
問:被加數至少是多少?例題精講【考點】加法數字謎 【難度】3星 【題型】填空【關鍵字】第四屆,華杯賽,初賽,第2題【解析】 從“被加數的數字和是和的數字和的三倍”這句話,可以推斷出兩點:①被加數可以被3整除。

数字谜从形式上可以分为横式数字谜与竖式数字谜,从运算法则上可以分为加减乘除四种形式的数字谜。
横式与竖式亦可以互相转换,本讲中将主要介绍数字谜的一般解题技巧。
主要涉及小数、分数、循环小数的数字谜问题,因此,会需要利用数论的知识解决数字谜问题一、数字迷加减法1.个位数字分析法2.加减法中的进位与退位3.奇偶性分析法二、数字谜问题解题技巧1.解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;2.要根据不同的情况逐步缩小范围,并进行适当的估算;3.题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性;4.注意结合进位及退位来考虑;模块一、加法数字谜【例 1】 “华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?0191杯华24+【例 2】 下面的算式里,四个小纸片各盖住了一个数字。
被盖住的四个数字的总和是多少?例题精讲知识点拨教学目标5-1-2-1.加减法数字谜1+49【例 3】在下边的算式中,被加数的数字和是和数的数字和的三倍。
问:被加数至少是多少?【例 4】两个自然数,它们的和加上它们的积恰为34,这两个数中较大数为().【例 5】下面的算式里,每个方框代表一个数字.问:这6个方框中的数字的总和是多少?1991+【例 6】在下边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数tavs ______v t s tt t v t t+【巩固】下面的字母各代表什么数字,算式才能成立?【巩固】右面算式中每一个汉字代表一个数字,不同的汉字表示不同的数字.当它们各代表什么数字时算式成立?【巩固】下面算式中,相同汉字代表相同数字,不同汉字代表不同数字,求“数学真好玩”代表的数是几?+爱好真知数学更好数学真好玩【例 7】下图是一个正确的加法算式,其中相同的字母代表相同的数字,不同的字母代表不同的数字.已知BAD不是3的倍数,GOOD不是8的倍数,那么ABGD代表的四位数是多少?B A D GO O D+【例 8】 在下面的算式中,汉字“第、十、一、届、华、杯、赛’,代表1,2,3,4,5,6,7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立.则“第、十、一、届、华、杯、赛’’所代表的7个数字的和等于 .+届赛6一杯0十华02第【例 9】 在下边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:+++d W V ☆=_______.+d d W W W W W W V V☆☆【例 10】 下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么A +B +C +D +E +F +G = 。
目录1、加减数字谜 (1)2、除法 (6)3、时间与日期 (11)4、和差问题 (16)5、乘法数字谜 (20)6、乘法巧算 (25)7、找规律计算 (30)8、对称图形 (36)9、最佳安排 (41)10、长方形和正方形的面积(一) (45)11、长方形和正方形的面积(二) (49)12、开放实践题 (53)13、移多补少与求平均数 (57)加减数字谜问题一、在□内填入合适的数字,使竖式成立。
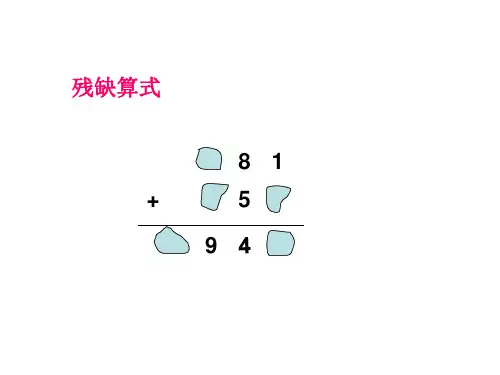
□ 9 1 + □ 1 □□ 9 1 □想:从最高位分析,必为1,因为两个数字相加中最大为9+9=18,而和要得19,所以十位必须想百位进一,而个位1只能加9,才能向十位进一满足十位进一后仍然得1的条件。
解:9 9 1+ 9 1 91 9 1 0点拨:(1)观察最高位,再看最低位,注意有进位。
(2)加法中两个数字相加,只能向前一位进一。
试一试在下面算式的空格内各填入一个合适的数字,使算式成立.□ 8 2 + □ 1 □□ 9 0 □□ 7 □+ □ 1 4□ 8 □□□ 9 □+ □ 1 1□ 7 1 □问题二、在下面算式的空格内各填入一个合适的数字,使算式成立.1 □+ □□ 5 □□□ 4 想:①从个位思考,5只有加9个位才得4,所以个位上应填9。
②再从百位思考,只有一个数字,相加的和要向千位进一,所以百位和千位只能是9、1。
③十位的数选择性比较多,只要和1相加有进位就可以,所以可以填8或9。
解: 1 9+ 9 8 51 0 0 4或 1 9+ 9 9 51 0 1 4点拨:从最低位算起,依次往前顺推,但要注意有进位。
试一试在下面算式的空格内各填入一个合适的数字,使算式成立.□ 8 7 + 9 □ 5 □ 8 5 46 4 □□+ □□ 7 8□ 0 2 6□□ 3+ 2 □□□□ 2问题三、在下面的算式内,各填上一个合适的数字,使等式成立。
□□□- □ 8 5 6 3 7 想:①个位:5+7=12,所以个位填2。
数字谜从形式上可以分为横式数字谜与竖式数字谜,从运算法则上可以分为加减乘除四种形式的数字谜。
横式与竖式亦可以互相转换,本讲中将主要介绍数字谜的一般解题技巧。
主要涉及小数、分数、循环小数的数字谜问题,因此,会需要利用数论的知识解决数字谜问题一、数字迷加减法1.个位数字分析法2.加减法中的进位与退位3.奇偶性分析法二、数字谜问题解题技巧1.解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;2.要根据不同的情况逐步缩小范围,并进行适当的估算;3.题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性;4.注意结合进位及退位来考虑;模块一、加法数字谜【例 1】 “华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?0191杯华24+【考点】加法数字谜 【难度】1星 【题型】填空 【关键词】华杯赛,初赛,第1题【例 2】 下面的算式里,四个小纸片各盖住了一个数字。
被盖住的四个数字的总和是多少?1+49例题精讲知识点拨教学目标5-1-2-1.加减法数字谜【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】华杯赛,初赛,第5题【例 3】 在下边的算式中,被加数的数字和是和数的数字和的三倍。
问:被加数至少是多少?【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】第四届,华杯赛,初赛,第2题【例 4】 两个自然数,它们的和加上它们的积恰为34,这两个数中较大数为( ). 【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】走美杯,3年级,初赛【例 5】 下面的算式里,每个方框代表一个数字.问:这6个方框中的数字的总和是多少?1991+【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】华杯赛,初赛,第11题【例 6】 在下边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数tavs =______s t v av t s t t t v t t +【考点】加法数字谜 【难度】2星 【题型】填空 【关键词】迎春杯,五年级,初赛,第5题【巩固】 下面的字母各代表什么数字,算式才能成立?DD D +ACDEE B EC B A【考点】加法数字谜 【难度】2星 【题型】填空【巩固】 右面算式中每一个汉字代表一个数字,不同的汉字表示不同的数字.当它们各代表什么数字时算式成立?+啊好是真好是真好啊好【考点】加法数字谜 【难度】2星 【题型】填空【巩固】 下面算式中,相同汉字代表相同数字,不同汉字代表不同数字,求“数学真好玩”代表的数是几?+爱好真知数学更好数学真好玩 【考点】加法数字谜 【难度】2星 【题型】填空【关键词】走美杯,初赛,六年级,第3题【例 7】 下图是一个正确的加法算式,其中相同的字母代表相同的数字,不同的字母代表不同的数字.已知BAD 不是3的倍数,GOOD 不是8的倍数,那么ABGD 代表的四位数是多少?B A DB A D G O O D+【考点】加法数字谜 【难度】3星 【题型】填空【例 8】 在下面的算式中,汉字“第、十、一、届、华、杯、赛’,代表1,2,3,4,5,6,7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立.则“第、十、一、届、华、杯、赛’’所代表的7个数字的和等于 .+届赛6一杯0十华02第【考点】加法数字谜 【难度】3星 【题型】填空 【关键词】华杯赛,初赛【例 9】在下边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:+++☆=_______.+☆☆【考点】加法数字谜 【难度】3星 【题型】填空【例 10】 下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么A +B +C +D +E +F +G = 。
三年级上学期第七讲,数字谜第01讲加减法填空格【内容概述】利用竖式运算法则和推理,通过观察、判断、推理、尝试把较简单的加减法竖式算式中缺少的数填出.【典型问题】1.【10701】(导引奇数题,三上第07讲加减法填空格,数字谜第01讲★)在图6-1算式的每个空格中,各填入一个合适的数字,使竖式成立.图6-1981+959=1940.提示:由于十位进位,第二个加数末尾必为9,和千位为1。
2.【10702】(导引偶数题,三上第07讲加减法填空格,数字谜第01讲★★)如图6-2,用0,1,2,3,4,5,6,7,8,9这10个数字各一次,可组成一个正确的加法竖式.现已写出3个数字,那么这个算式的结果是多少?图6-2764+289=1053.提示:和千位为1,百位不能是1,2,所以只能是0。
3.【10703】(导引奇数题,三上第07讲加减法填空格,数字谜第01讲★)在如图6-3所示的算式中,3个加数的各位数字均是某两个相邻数字中的一个,那么这个算式的计算结果可能是多少?1965,1975,1985,1995.三个加数的百位可能为6,6,6或6,6,7;个位数字和可能为5,15,25,对应有1,2,2或5,5,5或8,8,9;所以只能是百位数字为6,6,6,则个位数字为5,5,5,所以十位数字可能为5,5,5或5,5,6或5,6,6或6,6,6.4. 【10704】(导引偶数题,三上第07讲加减法填空格,数字谜第01讲★)在图6-4所示的算式中,被加数的数字和是和数的数字和的3倍.问:被加数至少是多少?18。
提示:个位有进位,不然被加数的数字和小于加数的数字和.5. 【10705】(导引奇数题,三上第07讲加减法填空格,数字谜第01讲★★)在图6-5所示的算式里,4张小纸片各盖住了一个数字.那么被盖住的4个数字总和是多少?14+9=23。
提示:个位无进位。
6. 【10706】(导引偶数题,三上第07讲加减法填空格,数字谜第01讲★★)在图6-6所示的算式里,每个方框代表一个数字.问:这6个方框中的数字的总和是多少?14 9 图6-5 +3 图6-4图6-31 9 9 1图6-647.可依次看出百位、十位、个位均有进位。
数字谜从形式上可以分为横式数字谜与竖式数字谜,从运算法则上可以分为加减乘除四种形式的数字谜。
横式与竖式亦可以互相转换,本讲中将主要介绍数字谜的一般解题技巧。
主要涉及小数、分数、循环小数的数字谜问题,因此,会需要利用数论的知识解决数字谜问题一、数字迷加减法1.个位数字分析法2.加减法中的进位与退位3.奇偶性分析法二、数字谜问题解题技巧1.解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异;2.要根据不同的情况逐步缩小范围,并进行适当的估算;3.题目中涉及多个字母或汉字时,要注意用不同符号表示不同数字这一条件来排除若干可能性;4.注意结合进位及退位来考虑;模块一、加法数字谜【例 1】 “华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?0191杯华24+【例 2】 下面的算式里,四个小纸片各盖住了一个数字。
被盖住的四个数字的总和是多少?1+49例题精讲知识点拨教学目标5-1-2-1.加减法数字谜【例 3】 在下边的算式中,被加数的数字和是和数的数字和的三倍。
问:被加数至少是多少?【例 4】 两个自然数,它们的和加上它们的积恰为34,这两个数中较大数为( ).【例 5】 下面的算式里,每个方框代表一个数字.问:这6个方框中的数字的总和是多少?1991+【例 6】 在下边的竖式中,相同字母代表相同数字,不同字母代表不同数字,则四位数tavs =______s t v av t s t t t v t t +【巩固】 下面的字母各代表什么数字,算式才能成立?DD D +AC DEE B ECBA【巩固】 右面算式中每一个汉字代表一个数字,不同的汉字表示不同的数字.当它们各代表什么数字时算式成立?+啊好是真好是真好啊好【巩固】 下面算式中,相同汉字代表相同数字,不同汉字代表不同数字,求“数学真好玩”代表的数是几?+爱好真知数学更好数学真好玩【例 7】 下图是一个正确的加法算式,其中相同的字母代表相同的数字,不同的字母代表不同的数字.已知BAD 不是3的倍数,GOOD 不是8的倍数,那么ABGD 代表的四位数是多少?B A DB A D G O O D +【例 8】 在下面的算式中,汉字“第、十、一、届、华、杯、赛’,代表1,2,3,4,5,6,7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立.则“第、十、一、届、华、杯、赛’’所代表的7个数字的和等于 .+届赛6一杯0十华02第【例 9】 在下边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出:+++ ☆=_______.+☆☆【例 10】 下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么A +B +C +D +E +F +G = 。
巧算加减法及加减法的竖式数字谜巧算加减法一、加法加法交换律:两个数相加,交换加数的位置,他们的和不变。
即:a+b=b+a其中a,b各表示任意一数.例如,7+8=8+7=15.总结:多个数相加,任意交换相加的次序,其和不变.加法结合律:三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再与第一个数相加,他们的和不变。
即:a+b+c=(a+b)+c=a+(b+c)其中a,b,c各表示任意一数.例如,5+6+8=(5+6)+8=5+(6+8).总结:多个数相加,也可以把其中的任意两个数或者多个数相加,其和不变。
二、减法在连减或者加减混合运算中,如果算式中没有括号,那么计算时要带数字前面的运算符号“搬家”.例如:a-b-c=a-c-b,a-b+c=a+c-b,其中a,b,c各表示一个数.在加减法混合运算中,去括号时:如果括号前面是“+”号,那么去掉括号后,括号内的数的运算符号不变;如果括号前面是“-”号,那么去掉括号后,括号内的数的运算符号“+”变为“-”,“-”变为“+”.如:a+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+c在加、减法混合运算中,添括号时:如果添加的括号前面是“+”,那么括号内的数的原运算符号不变;如果添加的括号前面是“-”,那么括号内的数的原运算符号“+”变为“-”,“-”变为“+”。
如:a+b-c=a+(b-c)a-b+c=a-(b-c)a-b-c=a-(b+c)三、加减法中的速算与巧算速算巧算的核心思想和本质:凑整1、分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.2、加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.3、数值原理法.先把加在一起为整十、整百、整千……的数相加,然后再与其它的数相加.4、“基准数”法,基准当几个数比较接近于某一整数的数相加时,选这个整数为“基准数”(要注意把多加的数减去,把少加的数加上)例题精讲一、加减速算【例1】计算:57911131517192123.【例 2】计算:(1)117+229+333+471+528+622(2)(1350+249+468)+(251+332+1650)(3)756-248-352(4)894-89-111-95-105-94【巩固】同学们,你们有什么好办法又快又准的算出下面各题的答案?把你的好方法讲一讲!也当一次小老师!⑴1847192862813664⑵1234567887661594322⑶200077415923⑷617271438315771二、加补凑整【例 3】计算:(1)298+396+495+691+799+21(2)195+196+197+198+199+15(3)98-96-97-105+102+101(4)399+403+297-501【例 4】199+298+397+496+595+20=___________。