最新大一-高等数学函数

大一数学函数知识点总结函数，在数学中占据着非常重要的地位。

在大一的数学学习中，我们对函数的认识和理解得到了进一步的拓展和加深。

下面我将对大一数学中的函数知识点进行总结，希望对你的学习有所帮助。

一、函数的概念与性质1. 函数的定义：函数是一种特殊的关系，将一个集合的元素与另一个集合的元素进行对应，使得每个元素在对应下有唯一结果。

2. 自变量与因变量：函数中自变量是指可以自由取值的变量，而因变量是根据自变量的取值决定的变量。

3. 定义域与值域：函数的定义域是指自变量的取值范围，值域是指因变量的所有可能取值。

4. 函数的性质：奇偶性、单调性、周期性等。

二、常见的函数类型1. 常数函数：f(x) = c (c为常数)，图像为一条水平直线。

2. 一次函数：f(x) = kx + b (k、b为常数)，图像为一条直线。

3. 幂函数：f(x) = x^a (a为常数)，图像的形状与a的正负、大小有关。

4. 指数函数：f(x) = a^x (a>0 且a≠1)，图像呈现指数增长或指数衰减趋势。

5. 对数函数：f(x) = log_a(x) (a>0 且a≠1)，图像与指数函数对称。

三、函数的运算1. 函数的加减运算：给定两个函数f(x)和g(x)，则它们的和函数为h(x) = f(x) + g(x)，差函数为h(x) = f(x) - g(x)。

2. 函数的乘积运算：给定两个函数f(x)和g(x)，则它们的乘积函数为h(x) = f(x) * g(x)。

3. 函数的复合运算：给定两个函数f(x)和g(x)，则它们的复合函数为h(x) = f(g(x))。

四、函数的图像与性质1. 函数的图像：通过画出函数的图像，可以更直观地了解函数的性质和变化趋势。

2. 函数的对称性：奇函数关于原点对称，偶函数关于y轴对称。

3. 函数的单调性：递增函数指的是函数随着自变量的增大，因变量也随之增大；递减函数指的是函数随着自变量的增大，因变量反而减小。

大一高数函数极限知识点函数极限是高等数学中的重要概念之一，它是分析函数性质和求解各种数学问题的基础。

在大一高数课程中，函数极限是必修内容，下面将介绍几个常见的函数极限知识点。

一、基本极限公式在求解函数极限的过程中，常用的基本极限公式有以下几个：1. 当n趋向于无穷大时，$\lim_{n \to \infty}\frac{1}{n^p} = 0$，其中p是大于0的实数。

2. 当x趋向于无穷大时，$\lim_{x \to \infty}\frac{1}{x^p} = 0$，其中p是大于0的实数。

3. $\lim_{x \to 0}\frac{sinx}{x} = 1$。

4. $\lim_{x \to \infty}(1+\frac{1}{x})^x = e$，其中e是自然对数的底数。

这些基本极限公式在求解各种函数极限时非常常用，熟练掌握它们可以简化计算过程。

二、函数极限的性质函数极限具有一些重要的性质，下面介绍两个常用的性质。

1. 函数极限的唯一性：如果$\lim_{x \to x_0}f(x) = A$，且$\lim_{x \to x_0}f(x) = B$，那么A=B。

即函数在某一点的极限存在时，它的极限值是唯一确定的。

2. 函数极限的四则运算法则：设$\lim_{x \to x_0}f(x) = A$，$\lim_{x \to x_0}g(x) = B$，其中A、B都存在，则有以下四则运算法则：（1）$\lim_{x \to x_0}[f(x) \pm g(x)] = A \pm B$（2）$\lim_{x \to x_0}[f(x) \cdot g(x)] = A \cdot B$（3）$\lim_{x \to x_0}\frac{f(x)}{g(x)} = \frac{A}{B}$，其中B不等于0。

这些性质在计算复杂函数极限时非常有用，可以简化计算步骤。

三、函数极限的求解方法对于一些特殊函数，我们需要使用一些特殊的求解方法来计算其极限。

大一高数函数详细知识点函数是数学中的重要概念，是现实世界中各种关系的抽象表达。

在大一的高数课程中，函数是一个核心内容，掌握了函数的基本概念和性质，对于后续学习以及应用数学都具有重要的意义。

本文将详细介绍大一高数中函数的知识点，以帮助读者更好地理解和掌握这一内容。

一、函数的定义和性质1. 定义：函数是一个将自变量和因变量之间的对应关系表示出来的规则。

通常用符号y=f(x)表示，其中x是自变量，y是因变量，f表示函数的关系。

2. 定义域和值域：函数的定义域是自变量所有可能取值组成的集合，值域是因变量的所有可能取值组成的集合。

3. 一一对应：如果函数中的每一个x值对应唯一的y值，且每一个y值也对应唯一的x值，则称这个函数是一一对应的。

4. 奇偶性：如果函数满足f(-x)=-f(x)（对于定义域内的所有x），则称这个函数是奇函数；如果函数满足f(-x)=f(x)（对于定义域内的所有x），则称这个函数是偶函数。

5. 函数的增减性：如果对于定义域内的任意两个实数x1和x2，当x1<x2时有f(x1)<f(x2)，则称函数是增函数；如果对于定义域内的任意两个实数x1和x2，当x1<x2时有f(x1)>f(x2)，则称函数是减函数。

二、常见的基本函数类型1. 线性函数：线性函数的表达式为y=kx+b，其中k和b为常数。

线性函数的图像为一条直线，斜率k决定了直线的倾斜程度，常数b决定了直线与y轴的交点。

2. 幂函数：幂函数的表达式为y=x^a，其中a为常数。

幂函数的图像关于y轴对称，当a为正数时，函数是递增的；当a为负数时，函数是递减的。

3. 指数函数：指数函数的表达式为y=a^x，其中a为常数且大于0且不等于1。

指数函数的图像为一条曲线，当a大于1时，函数是递增的；当0<a<1时，函数是递减的。

4. 对数函数：对数函数的表达式为y=logₐx，其中a为常数且大于0且不等于1。

高数1函数知识点总结大一高数1函数知识点总结高数1是大一学生必修的一门数学课程，其中的函数是重要的内容之一。

在学习函数的过程中，我们需要了解和掌握一些关键的知识点。

本文将对高数1中的函数知识点进行总结，以帮助同学们更好地理解和应用这些知识。

一、函数的概念及表示法函数是自变量和因变量之间的一种对应关系。

一般用字母f或g等表示函数名，自变量用x表示，函数表达式写作f(x)，表示因变量与自变量的对应关系。

二、函数的定义域和值域函数的定义域是指自变量的取值范围，值域是指函数在定义域内所有可能的因变量值。

在求解函数的定义域时，需要注意不可除以零的情况，以及根式中不能出现负数的情况。

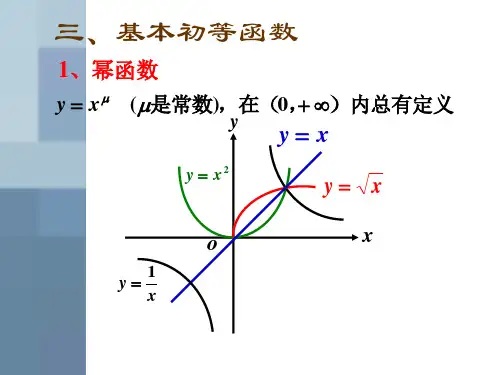
三、基本初等函数高数1中常见的基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数等。

这些函数具有特定的函数表达式和性质，需要熟记其定义和基本性质。

四、函数的图像与性质函数的图像是函数表达式在坐标系中的几何表示。

通过观察函数图像，我们可以推测函数的增减性、奇偶性、周期性等性质。

在绘制函数图像时，需要注意选择合适的坐标轴范围和绘制方法，以便准确反映函数的特点。

五、函数的运算函数可以进行加减乘除等基本运算，也可以进行复合和反函数运算。

在进行函数的复合运算时，需要注意确保复合函数的定义域和值域的合法性，同时注意求解反函数时的一一对应关系。

六、函数的极限函数的极限是数列极限的推广，用来研究函数在某一点的趋势。

函数的左极限和右极限可以让我们了解函数在某一点处的接近情况。

在求解极限时，可以运用极限的性质和极限运算法则来简化计算过程。

七、导数与微分导数是函数在某一点处的变化率，表示函数图像在该点的切线斜率。

导数的计算需要用到极限的概念，可以运用一些常见函数的求导法则简化计算。

微分则是导数的微小变化量，可以应用于函数的近似计算和优化问题。

八、函数的应用函数是数学在实际问题中的重要工具，具有广泛的应用价值。

在物理学、经济学、工程学等领域，函数被用于建立数学模型，描述和解决各种实际问题。

大一数学函数知识点总结与归纳数学函数是大一数学课程中的重要内容之一，它是数学建模和解决实际问题的基础。

在学习函数的过程中，我们需要了解和掌握一些重要的知识点。

本文将总结和归纳大一数学函数的相关知识点，帮助读者更好地理解和应用函数。

一、函数的定义函数是一个表达式，它把一个或多个自变量映射到一个或多个因变量上。

函数的定义包括定义域、值域和对应关系。

例如，函数f(x) = x^2定义域为所有实数，值域为非负实数集合。

二、常见的数学函数1.线性函数线性函数表达式为f(x) = kx + b，其中k和b为常数。

它的图像是一条直线，具有恒定的斜率。

2.二次函数二次函数表达式为f(x) = ax^2 + bx + c，其中a、b和c为常数，且a ≠ 0。

它的图像是一个开口向上或向下的抛物线，又称为U型曲线。

3.指数函数指数函数表达式为f(x) = a^x，其中a为常数且a > 0，且a ≠ 1。

它的图像是一个逐渐增长或递减的曲线，具有特定的底数。

4.对数函数对数函数表达式为f(x) = loga(x)，其中a为常数且a > 0，且a ≠ 1。

它的图像是一个逐渐平缓或陡峭的曲线，是指数函数的反函数。

5.三角函数三角函数包括正弦函数、余弦函数和正切函数等。

它们的周期性和波动性使得它们在物理、工程和自然科学中具有广泛的应用。

三、函数的性质和图像1.奇偶性如果函数满足f(-x) = -f(x)，则称该函数为奇函数；如果函数满足f(-x) = f(x)，则称该函数为偶函数。

2.单调性一个函数在定义域上是递增的，如果对于任意的x1 < x2，有f(x1) < f(x2)。

一个函数在定义域上是递减的，如果对于任意的x1 < x2，有f(x1) > f(x2)。

3.极值点和拐点函数的极大值点是在该点上函数取得最大值的点，极小值点是在该点上函数取得最小值的点。

而拐点则是函数图像由凹转凸或由凸转凹的点。

大一高数函数知识点总结一、函数的定义与性质在数学中，函数是指两个集合之间的对应关系。

通常用符号f(x) 表示，其中 x 是自变量，f(x) 是对应的函数值或因变量。

函数的性质包括以下几个方面：1. 定义域与值域：函数的定义域是自变量可能取值的集合，而函数值域是所有可能的函数值所组成的集合。

2. 单调性：函数可以是递增的（单调增函数）或者递减的（单调减函数）。

3. 奇偶性：函数可以是奇函数（满足 f(-x) = -f(x)）或偶函数（满足 f(-x) = f(x)）。

4. 周期性：函数可以具有周期性，即存在一个正数 T，满足f(x+T) = f(x)。

5. 最大值与最小值：函数的最大值是函数值域中的最大元素，最小值是函数值域中的最小元素。

二、常见的函数类型1. 基本初等函数：包括常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数等。

- 常数函数：f(x) = c，其中 c 是常数。

- 幂函数：f(x) = x^n，其中 n 是整数。

- 指数函数：f(x) = a^x，其中 a 是正实数且不等于 1。

- 对数函数：f(x) = log_a(x)，其中 a 是正实数且不等于 1。

- 三角函数：包括正弦函数、余弦函数、正切函数等。

- 反三角函数：包括反正弦函数、反余弦函数、反正切函数等。

2. 反函数：如果两个函数 f(x) 和 g(x) 满足 f(g(x)) = x 和 g(f(x))= x，那么它们互为反函数。

3. 复合函数：复合函数是指将一个函数的输出作为另一个函数的输入得到的函数。

4. 无穷大与无穷小：在函数的极限中，可以存在无穷大或无穷小的情况。

5. 参数方程与极坐标方程：函数可以通过参数方程或极坐标方程来表示。

三、函数的运算函数之间可以进行多种运算，包括加法、减法、乘法和除法等。

1. 加法和减法：对于函数 f(x) 和 g(x)，它们的和为 (f+g)(x) =f(x) + g(x)，差为 (f-g)(x) = f(x) - g(x)。

大一数学函数知识点大汇总函数是数学中一个非常基础且重要的概念，它在数学和实际应用中都有广泛的应用。

在大一的数学学习中，函数是一个重点和难点。

今天我们来对大一数学中常见的函数知识点进行一个大汇总。

一、函数的定义和符号表示函数是一种特殊的关系，它将一个自变量的值映射到一个或多个因变量的值。

函数的定义通常表示为：```f: X → Y```其中，X 和 Y 分别表示自变量和因变量的取值集合，箭头表示函数的映射关系。

二、函数的分类根据函数的性质和表达式，可以将函数分为以下几类：1. 常数函数：函数的值在定义域上是唯一的常数。

例如：`f(x) = 2`2. 一次函数：函数的表达式是一次多项式。

例如：`f(x) = ax + b`3. 幂函数：函数的表达式是 x 的幂次。

例如：`f(x) = x^n`4. 指数函数：函数的表达式是以常数 e 为底的指数幂。

例如：`f(x) = e^x`5. 对数函数：函数的表达式是常数为底的对数。

例如：`f(x) = logₐ(x)`6. 三角函数：函数的表达式是三角函数。

例如：`f(x) = sin(x)`7. 反三角函数：函数的表达式是反三角函数。

例如：`f(x) = arcsin(x)`8. 绝对值函数：函数的表达式是自变量的绝对值。

例如：`f(x) = |x|`9. 双曲函数：函数的表达式是双曲函数。

例如：`f(x) = sinh(x)`三、函数的性质函数在数学中有一些重要的性质，下面我们来了解几个常见的性质：1. 定义域和值域：函数的定义域是自变量的取值范围，值域是因变量的取值范围。

2. 奇偶性：函数的奇偶性描述了函数在坐标系中的对称性。

3. 单调性：函数的单调性描述了函数值随自变量增大或减小的趋势。

4. 极值和最值：函数的极值是函数在某一区间内的最高点或最低点，最值是函数在整个定义域内的最高点或最低点。

5. 对称轴和零点：函数的对称轴是函数图像的对称轴线，零点是函数的因变量为零的自变量值。

大一高数函数与极限知识点函数与极限是高等数学中的重要基础知识，它们在数学和其它科学领域中有着广泛的应用。

本文将介绍大一高数中与函数与极限相关的几个重要知识点。

一、函数的概念与性质函数是一种特殊的关系，对于一个定义域内的每一个自变量，它都有唯一对应的因变量。

函数的定义域、值域、图像以及函数的性质都是我们需要了解的内容。

1.1 函数的定义域和值域函数的定义域是指所有使函数有意义的自变量的取值范围，而值域是函数在定义域内可能取到的所有因变量的值。

在确定定义域时，需要避开函数中会导致分母为零或根号内出现负数的取值。

1.2 函数的图像函数的图像是在直角坐标系中表示函数的一种方式，横坐标表示自变量，纵坐标表示因变量。

通过观察函数的图像，我们可以了解函数的增减性、奇偶性等性质。

二、极限的概念与运算规则极限是函数与自变量无限接近某个值时的性质，它在数学中应用广泛，尤其是在微积分中发挥着重要作用。

2.1 极限的定义对于一个函数，当自变量无限接近某个值时，如果因变量的取值可以无限接近于一个确定的常数L，那么我们就说该函数的极限为L。

用数学符号表示为lim(f(x))=L。

2.2 极限的运算规则极限具有一些运算规则，如常数与函数的极限相乘、函数相加的极限等，可以方便地求解复杂的极限问题。

三、常见的函数与极限在大一高数中，我们常常遇到一些基本的函数与极限，包括多项式函数、指数函数、对数函数以及三角函数的极限等。

3.1 多项式函数的极限多项式函数是由常数项、幂次项以及它们的和、差、积构成的函数。

求解多项式函数的极限可以通过代入法、化简或者利用极限的运算规则等方法进行。

3.2 指数函数和对数函数的极限指数函数与对数函数也是我们常见的函数类型，求解它们的极限需要运用一些特定的方法，如利用指数函数与对数函数的反函数关系、换元法等。

3.3 三角函数的极限三角函数在数学和物理中有着重要的地位，求解三角函数的极限需要掌握一些基本的极限公式，如sinx/x的极限等。

大一数学函数知识点归纳数学函数是大一学生学习数学必不可少的知识点。

函数是描述两个数集之间对应关系的一种工具，具有广泛的应用价值。

下面将对大一数学函数的知识点进行归纳总结。

一、函数的定义与表示方式函数是一种映射关系，通常表示为f(x)，其中x是自变量，f(x)是因变量。

函数可以用多种方式表示，包括函数图像、函数表格和函数公式等。

二、函数的基本性质1. 定义域和值域：函数的定义域是自变量的取值范围，值域是因变量的取值范围。

2. 奇偶性：函数的奇偶性指函数关于坐标轴的对称性，可用函数的公式来判断。

3. 单调性：函数的单调性指函数在定义域上的增减性质，可通过导数或函数的图像来判断。

4. 周期性：具有周期性的函数在一定范围内的取值规律是相同的，可用函数的公式或函数的图像来判断。

5. 特殊函数：特殊函数包括常数函数、线性函数、幂函数、指数函数、对数函数、三角函数等，它们具有特殊的性质和图像。

三、函数的运算与复合函数1. 四则运算：函数可以进行加减乘除等运算，保持函数性质。

2. 反函数：若函数f(x)的定义域、值域与f(x)相互对应，则称f(x)的反函数为f^(-1)(x)。

3. 复合函数：当一个函数的自变量是另一个函数时，可以得到复合函数，如f(g(x))。

四、函数的极限与连续性1. 函数的极限：函数的极限是函数在某一点或无穷远处的取值情况，常用于描述函数的趋势。

2. 函数的连续性：函数在某一点连续表示函数在该点的函数值与它的极限值相等。

五、函数的导数与微分1. 函数的导数：函数的导数表示函数在某一点的变化率，可用于刻画函数图像的斜率。

2. 函数的微分：函数的微分表示函数在某一点附近的局部线性逼近。

六、常见函数的应用1. 刚体运动：位移、速度、加速度等物理量可用函数来描述。

2. 统计学：概率密度函数、累积分布函数等统计函数在数据分析中具有重要应用。

3. 经济学：成本函数、收益函数等在经济学中用于分析成本与收益的关系。

大学高等数学第一章函数函数是数学中的基础概念之一，广泛应用于各个学科领域。

本文将从函数的定义、分类和性质等方面进行论述，并探讨函数在现实生活和学术研究中的应用。

一、函数的定义函数是一种映射关系，将一个集合的每个元素都对应到另一个集合的唯一元素。

简单来说，函数就是一种输入和输出之间的关系。

数学上常用 f(x) 表示函数，其中 x 是自变量，f(x) 是函数的值。

二、函数的分类函数可以按照不同的变量类型进行分类，常见的分类包括：1. 数字函数：自变量和函数值都是实数的函数，如 f(x) = 2x + 1。

2. 向量函数：自变量是实数，函数值是向量的函数，如 f(t) = (cos t, sin t)。

3. 多元函数：自变量是多个实数，函数值是实数的函数，如 f(x, y) = x^2 + y^2。

4. 参数方程：自变量是参数，函数值是一组参数对应的点的坐标，如 x = 2t, y = 3t。

三、函数的性质函数具有以下一些重要性质：1. 定义域和值域：函数的定义域是自变量的取值范围，值域是函数值的取值范围。

2. 奇偶性：如果对于定义域内的任意 x，满足 f(-x) = -f(x)，则函数是奇函数；如果满足 f(-x) = f(x)，则函数是偶函数。

3. 单调性：如果对于任意的 x1 和 x2，当 x1 < x2 时有 f(x1) < f(x2)，则函数是递增函数；如果满足 f(x1) > f(x2)，则函数是递减函数。

4. 对称轴和顶点：对于二次函数 y = ax^2 + bx + c，它的对称轴是 x = -b/2a，顶点坐标为 (-b/2a, f(-b/2a))。

四、函数的应用函数在现实生活和学术研究中有着广泛的应用。

以下是一些例子：1. 物理学：函数用于描述运动过程中的位移、速度和加速度等物理量的关系。

2. 经济学：函数被用于模拟经济行为和预测市场走势，如供求函数、收益函数等。

大一上高数重点知识点一、函数与极限1.函数：-函数的定义：函数是一个变量间的关系，通常表示为y=f(x)，其中x是自变量，y是因变量，f(x)是给定x的函数值。

-四则运算和复合运算：加法、减法、乘法、除法、复合等运算规则。

-基本初等函数：常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数等。

2.极限：-极限的定义：当自变量x无限接近一些确定值时，函数f(x)的值逐渐趋向于一个确定的常数L，称L为函数f(x)当x趋近于一些确定值时的极限。

-极限的性质：极限的唯一性、局部有界性、保序性等。

-极限计算法则：四则运算法则、复合运算法则、等价无穷小替代法则等。

二、导数与微分学1.导数：- 导数的定义：函数f(x)在点x处的导数表示为f'(x)，定义为f'(x)=lim(x→0)(f(x+h)-f(x))/h。

-导数的几何意义：导数表示函数的变化率，即函数曲线在一点的斜率。

-基本求导法则：常数法则、乘法法则、幂函数法则、指数函数法则、对数函数法则、三角函数法则等。

2.微分学：- 微分的定义：函数f(x)在点x处的微分表示为df(x)=f'(x)dx。

-微分的几何意义：微分代表函数曲线在特定点附近的线性近似，即切线与x轴的交点的y坐标。

-高阶导数：导数的导数称为高阶导数，如f''(x)表示f'(x)的导数。

三、不定积分与定积分1.不定积分：- 不定积分的定义：函数F(x)是f(x)的一个原函数，表示为∫f(x)dx=F(x)+C，其中C为常数。

-基本积分法则：幂函数积分、指数函数积分、对数函数积分、三角函数积分等。

-分部积分法：将积分的乘积分解为两个函数的乘积的积分形式进行求解。

-特殊积分：标准形式的积分表达式的求解，如三角函数的积分、有理函数的积分等。

2.定积分：- 定积分的定义：函数f(x)在区间[a,b]上的定积分表示为∫[a,b]f(x)dx，表示函数在该区间上的面积。

大一高数函数知识点函数是高等数学中的重要概念，它是描述数学关系的一种工具。

在大一的高等数学课程中，学生们会接触到许多与函数相关的知识点。

本文将介绍大一高数中的一些常见函数知识点，帮助读者更好地理解和掌握这些概念。

一、函数的定义与性质函数是一种映射关系，将一个集合中的每个元素都唯一地对应到另一个集合中的元素。

函数通常用符号表示，如f(x)或y=f(x)。

其中，x称为自变量，y称为因变量。

函数的定义包括定义域、值域和对应关系三个要素。

例如，对于函数y=x^2，其定义域为所有实数集R，值域为非负实数集R+，对应关系为x和x^2之间的关系。

函数的性质包括奇偶性、周期性等。

奇函数满足f(-x)=-f(x)，即图像关于y轴对称；偶函数满足f(-x)=f(x)，即图像关于原点对称。

周期函数具有在一定范围内重复出现的特点。

二、常见函数类型1. 线性函数线性函数是最简单的一类函数，其表达式为y=kx+b，其中k和b为常数。

线性函数的图像为斜率为k的直线，b为截距。

2. 幂函数幂函数是指以x为底的幂指数函数，其表达式为y=a*x^b，其中a和b为常数。

a决定了函数图像的纵向方向，b决定了函数图像的形状。

3. 指数函数指数函数是以常数e为底的指数函数，其表达式为y=a*e^x，其中a为常数。

指数函数的图像在x轴右侧呈现逐渐增大的趋势。

4. 对数函数对数函数是指数函数的反函数，其表达式为y=logₐ(x)，其中a为常数。

对数函数的图像在x轴上仍然是逐渐增大的趋势，但增长速度逐渐减慢。

5. 三角函数三角函数包括正弦函数、余弦函数和正切函数等。

它们都是周期函数，具有一定的振荡特性。

三、函数的运算与复合函数函数之间可以进行加减乘除等运算，生成新的函数。

例如，两个函数f(x)和g(x)的和为h(x)=f(x)+g(x)，差为j(x)=f(x)-g(x)。

函数的乘积与商的定义也类似。

复合函数是指将一个函数的输出作为另一个函数的输入，生成新的函数。

高等数学知识点总结大一大一高等数学知识点总结。

一、函数与极限。

1. 函数。

- 定义：设数集D⊆ R，则称映射f:D→ R为定义在D上的函数，通常记为y = f(x),x∈ D。

- 函数的特性。

- 有界性：若存在M>0，使得对任意x∈ X⊆ D，都有| f(x)|≤ M，则称f(x)在X上有界。

- 单调性：设函数y = f(x)的定义域为D，区间I⊆ D。

如果对于区间I上任意两点x_1及x_2，当x_1 < x_2时，恒有f(x_1)（或f(x_1)>f(x_2)），则称函数y =f(x)在区间I上是单调增加（或单调减少）的。

- 奇偶性：设函数y = f(x)的定义域D关于原点对称，如果对于任意x∈D，有f(-x)=f(x)，则称f(x)为偶函数；如果对于任意x∈ D，有f(-x)= - f(x)，则称f(x)为奇函数。

- 周期性：设函数y = f(x)的定义域为D，如果存在一个正数T≠0，使得对于任意x∈ D有(x± T)∈ D，且f(x + T)=f(x)，则称y = f(x)为周期函数，T称为y = f(x)的周期。

- 复合函数：设函数y = f(u)的定义域为D_1，函数u = g(x)在D上有定义且g(D)⊆ D_1，则由下式确定的函数y = f[g(x)],x∈ D称为由函数u = g(x)与函数y = f(u)构成的复合函数，它的定义域为D，变量u称为中间变量。

- 反函数：设函数y = f(x)的定义域为D，值域为W。

如果对于值域W中的任一y值，从关系式y = f(x)中可确定唯一的一个x值，则称变量x为变量y的函数，记为x = f^-1(y)，y∈ W，称x = f^-1(y)为函数y = f(x)的反函数。

习惯上y = f(x)的反函数记为y = f^-1(x)。

2. 极限。

- 极限的定义。

- 数列极限：设{x_n}为一数列，如果存在常数a，对于任意给定的正数varepsilon（不论它多么小），总存在正整数N，使得当n > N时，不等式| x_n - a|都成立，那么就称常数a是数列{x_n}的极限，或者称数列{x_n}收敛于a，记为lim_n→∞x_n=a。