下载文档原格式
小学三年级奥数精品讲义目录第一讲加减法的巧算（一）第二讲加减法的巧算（二）第三讲乘法的巧算第四讲配对求和第五讲找简单的数列规律第六讲图形的排列规律第七讲数图形第八讲分类枚举第九讲填符号组算式第十讲填数游戏第十一讲算式谜（一）第十二讲算式谜（二）第十三讲火柴棒游戏（一）第十四讲火柴棒游戏（二）第十五讲从数量的变化中找规律第十六讲数阵中的规律第十七讲时间与日期第十八讲推理第十九讲循环第二十讲最大和最小第二十一讲最短路线第二十二讲图形的分与合第二十三讲格点与面积第二十四讲一笔画第二十五讲移多补少与求平均数第二十六讲上楼梯与植树第二十七讲简单的倍数问题第二十八讲年龄问题第二十九讲鸡兔同笼问题第三十讲盈亏问题第三十一讲还原问题第三十二讲周长的计算第三十三讲等量代换第三十四讲一题多解第三十五讲总复习第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军，都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报，台下的观众频频为选手取得的好成绩而热烈鼓掌，同时，观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中，就像变魔术般地得出了答案。
等小熊满头大汗地算出来时，小白兔已欣赏了一阵比赛，结果每次小熊算得结果和小白兔是一样的。
小熊不禁问：“白兔弟弟，你这么快就算出了答案，有什么决窍吗”小白兔说：“比如2号选手是93、95、98、96、88、89、87、91、93、91，去掉最高分98，去掉最低分87，剩下的都接近90为基准数，超过90的表示成90+‘零头数’，不足90的表示成90－‘零头数’。
于是（93+95+96+88+89+91+93+91）÷8=90+（3+5+6―2―1+1+3+1）÷8=90+2=92。
你可以试一试。
”小熊照着小白兔说的去做，果然既快又对。
这下小熊明白了，掌握了速算的技巧，在工作和生活中的作用很大。
【我生命中最最最重要的朋友们，请你们认真听老师讲并且跟着老师的思维走。
学业的成功重在于考点的不断过滤，相信我赠予你们的是你们学业成功的过滤器。
谢谢使用！！！】找规律（一）一、考点、热点回顾1、什么是“数列”，如何发现和寻找“数列”的规律。
2、按一定次序排列的一列数就叫数列。
例如，(1) 1，2，3，4，5，6，…(2) 1，2，4，8，16，32；(3) 1，0，0，1，0，0，1，…(4) 1，1，2，3，5，8，13。
3、一个数列中从左至右的第n个数，称为这个数列的第n项。
如，数列(1)的第3项是3，数列(2)的第3项是4。
一般地，我们将数列的第n项记作a n。
4、数列中的数可以是有限多个，如数列(2)(4)，也可以是无限多个，如数列(1)(3)。
5、自然数数列：按照自然数从小到大的次序排列。
其规律后项=前项+1，或第n项a n＝n。
例如，数列(1)。
数列(2)的规律是：后项=前项×2，或第n项数列(3)的规律是：“1，0，0”周而复始地出现。
数列(4)的规律是：从第三项起，每项等于它前面两项的和，即a3=1+1=2，a4=1+2=3，a5=2+3＝5，a6=3+5=8，a7=5+8=13。
6、有穷数列：根据数列中项的个数分类，项数有限的数列（即有有穷多个项的数列）。
7、无穷数列：把项数无限的数列（即有无穷多个项的数列）。
例如：（1）自然数：1，2，3，4，5，6，7，…（2）年份：1990，1991，1992，1993，1994，1995，1996（3）某年级各班的学生人数（按班级顺序一、二、三、四、五班排列）45，45，44，46，458、常见的较简单的数列规律有这样几类：第一类是数列各项只与它的项数有关，或只与它的前一项有关。
例如数列(1)(2)。
第二类是前后几项为一组，以组为单元找关系才可找到规律。
例如数列(3)(4)。
第三类是数列本身要与其他数列对比才能发现其规律。
这类情形稍为复杂些，我们用后面的例3、例4来作一些说明。
第7讲平均数一组数的和除以这组数的个数,称为这组数的平均数。
例1、5个连续自然数的中间一个数是45,这5个数的和是多少?分析5个连续自然数的第3个数是45,第2个(44)与第4个(46)相加是两个45,第1个(43)与第5个(47)相加是两个45。
解和是45×5=225随堂练习1计算56+57+58+59+60+61+62+63+64一般地,奇数个连续自然数的和等于中间一项乘以项数。
换句话说,奇数个连续自然数的平均数就是中间的那个数。
高斯求和方法的实质就是和=平均数×项数偶数个连续自然数的平均数不是整数,我们现在尚未学到。
所以先将第一项加最后一项,第二项加倒数第二项……直至中间两项相加,这些和都相等。
而个数是项数的一半,所以偶数个连续自然数的和等于中间两项的和(也即首末两项的和)乘以项数除以2.例2、8个连续自然数的和是108,写出这8个数。
分析因为中间两个数相加再乘以4(=8÷2)等于108,所以中间两项的和可以求出来。
解中间两项的和是108÷(8÷2)=27又27=13+14所以中间两项是13、14.这8个数是10、11、12、13、14、15、16、17.(由13往前数4个数到10,由14往后数4个数到17)答:这8个连续的自然数是10、11、12、13、14、15、16、17.随堂练习26个连续自然数的和是273,这6个数中的第一个数是多少?例3、求出以下28个数的平均数:12、13、13、14、15、16、16、16、17、18、19、20、21、22、23、24、25、26、27、28、29、30、31、32、33、34、35、35.分析与解这28个数的和是(12+13+14+……+35)+13+16+16+35求出和再除以28就得到平均数,但比较麻烦。
如果注意到25个连续自然数11、12、13,……,35的平均数是23(中间一项),那么就比较容易。
三秋第5讲周期问题（二）——寻找隐藏周期一、教学目标在日常生活中，有一些按照一定规律不断重复出现的现象。
例如：一周中的星期几，人的属相等，像这种的一些元素按照一定的规律依次不断重复出现的，我们把其中一组重复出现的元素称为周期。
周期特征：每一组相同的周期所包含的元素数量是一样的，每一组周期中元素排列的顺序都是一样的。
周期方法：先利用周期的特性，将元素按照统一的周期进行分组，然后再按照要求得出需要的结论。
研究周期性问题时，不仅要判断不断重复出现的规律，而且要找出这个固定的“周期”，这样就可以使周期问题转化成较简单的问题了。
有的时候周期不能直接看出，需要通过枚举的方法找到周期。
二、例题精选【例1】如图,电子跳蚤每跳一步,可以从一个圆圈跳到相邻的圆圈.现在,一只红跳蚤从标有“1”的圆圈按顺时针方向跳了50下,落在一个圆圈里.一只黑跳蚤也从标有数“1”的圆圈起跳,但它是沿着逆时针方向跳了60下,落在另一个圆圈里.问：这两个圆圈里整数的乘积是多少?【巩固1】在下图中，一个人从A点出发，按顺时针方向绕五边形走，到E点拐第一个弯，到D点拐第二个弯，……，问：在什么地方拐第47个弯？【例2】伸出你的左手，从大拇指开始如图所示的那样数数字，1，2，3，…，问：数到70时，正好数在______指上。
【巩固2】钟表上现在时针正对着2点，那么再过45小时后，时针会对着哪个数字？【例3】40位同学从左到右排成一行，然后按如下规律从左向右报数：先让第一位同学报1，然后从第二位同学开始，每位同学都把前一位同学所报的数乘以7，再报出乘积的个位来．请问：第40个同学报的是几？【巩固3】37位同学从左到右排成一行，然后按如下规律从左向右报数：先让第一位同学报6，然后从第二位同学开始，每位同学都把前一位同学所报的数乘以2，再报出乘积的个位来．请问：第37个同学报的是几？【例4】五位同学围成一圈依次循环报数，规定，第一位同学首次报出的数为2，第二位同学首次报出的数为3，之后每位同学所报出的数都是前两位同学所报出数的乘积的个位数字，则第50个被报出的数是几？【巩固4】40位同学排成一行，从左向右报数：先让第一位同学报2，第二位同学报7，然后从第三位同学开始，每位同学都把前两位同学所报的数相乘，再报出乘积的个位来．那么最后一位同学报的是几？【例5】甲、乙、丙、丁四兄弟四人各收藏一些宝石．每天早上他们都要聚在一起，重新分配宝石，分配的规则是：拥有宝石最多的人分给其他三人每人1颗．如果第1天早上分配完之后，甲、乙、丙、丁四人分别有10、7、5、4颗宝石，那么第39天早上分完宝石后，四个人手中分别有几颗宝石？【巩固5】甲、乙、丙三个兄弟分宝石，规定每天宝石最多的人给其他人每人一颗。
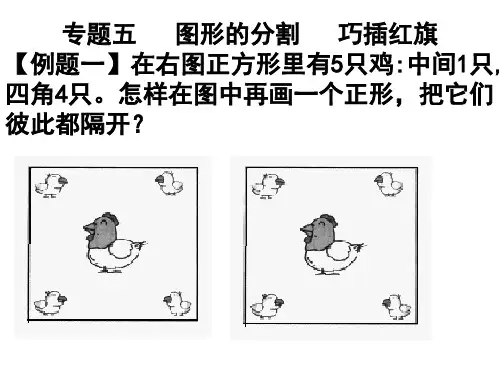
二年级1.找出图形变化的规律，并画出第四幅图。
2.计算：28+208+2008+20008三年级1.一条马路长200米，在马路两侧每隔4米种一棵树，则一共要种多少棵树？2.移动一根火柴棍，使得算式成立。
四年级1.王刚、李强和小莉、小芳是两对夫妻，四人的年龄和是132岁。
丈夫都比自己的妻子大5岁，李强比小芳大6岁。
小莉多少岁？2.第一个图形由4根火柴棍组成，第二个图形由12根火柴棍组成，第三个图形由24根火柴棍组成，依此类推，第100个图形由多少根火柴棍组成？五年级1.将15拆成若干个互不相同的自然数之和，要求这些自然数的乘积尽量大，那么积是多少？2.将各位数字都不大于5的非0自然数，从小到大排列，第2010个数是多少？六年级1.中午12时，校准A、B、C三钟。
当天下午A钟6点时，B钟5点50分；B钟7点时，C钟7点20分。
那么当晚C钟11点时，A钟是几点几分？2.在16点16分0秒时，钟表盘上时针和分针的夹角是多少度？数论综合1. 把一个两位数质数写在另一个两位数质数右边，得到一个四位数，它能被这两个质数之和的一半整除，那么这样的两个质数乘积最大是______;2.两数乘积为2800，而且已知其中一数的约数个数比另一数的约数个数多1。
那么这两个数分别是____、____;3. 两个不同的数，它们的最小公倍数是90，那么这样的两个数共有______组;4. 有三条圆形跑道，甲、乙、丙三人分别在里圈、中圈、外圈沿相同方向跑步。
里圈跑道长0.35千米，中圈长0.5千米，外圈长0.75千米。
甲每小时跑6千米，乙每小时跑7. 5千米，丙每小时跑10千米。
他们同时从A点出发，那么______分钟后三人第一次同时位于图中水线上;5. c的最小值为_______;+b+三角形的三边长a、b、c均为整数，且a、b、c的最小公倍数为60，a、b的最大公约数为4，b、c的最大公约数为3，那么a6. 用2、3、4、5、6、7这六个数码组成两个三位数A和B，那么A、B、540这三个数的最大公约数最大可能是______;7. 已知三个两位奇数，它们的最大公约数是1，但是两两均不互质，且三个数的最小公倍数共有18个约数，那么这三个数可以为____、____、____;8. 一个自然数除以7、8、9后分别余3、5、7，而所得的三个商的和是758，这个数是_______;9. 甲、乙、丙三数分别为526、539、705。
