全等三角形做辅助线-倍长中线,截长补短课程教案

-组织小组合作学习，让学生在讨论和互助中共同探究截长补短法的应用。
-通过小组间的交流，分享解题思路和经验，提高学生之间的相互学习和借鉴。
4.实践操作，加深理解：
-安排尺规作图实践，让学生动手操作，加深对截长补短法的理解和记忆。
-教师巡回指导，及时纠正学生在作图和证明过程中的错误，确保学习效果。
5.反思评价，促进成长：
-在复杂问题中识别应用截长补短法的时机，并能够结合全等三角形的判定定理进行有效证明。
-对于一些非标准图形，能够创造性地运用截长补短法，培养学生的创新思维和解决问题的能力。
（二）教学设想
1.创设情境，引入新课：
-通过展示一些生活中的实际例子，如建筑设计中的几何图形，引出全等三角形的应用。
-设计问题，让学生在实际情境中发现全等三角形，并感受到截长补短法在解决问题时的便捷性。
2.教学实施：
-分组讨论：将学生分成小组，每组分配一个或多个问题，要求运用截长补短法解决。
-教师巡回指导：观察学生的讨论过程，适时给予提示和指导，引导学生深入思考。
-小组分享：鼓励各小组展示解题过程和结果，其他小组给予评价和反馈。
（四）课堂练习
1.教学设计：设计具有梯度性的练习题，让学生独立完成，巩固所学知识。
-鼓励学生在课后进行反思，总结截长补短法在解决问题时的优势和局限。
-通过自我评价和同伴评价，帮助学生认识自身的进步和需要提升的地方，促进他们的个性化发展。
四、教学内容与过程
（一）导入新课
1.教学设计：通过生活实例和问题情境，自然导入新课——截长补短法在全等三角形中的应用。
-展示图片：呈现一些包含全等三角形的生活场景，如建筑物的立面图、拼图游戏等。
人教版数学八年级上册第12章全等三角形专题课截长补短法教学设计

在本节课的教学过程中，我注重引导学生主动参与，激发他们的学习兴趣。通过截长补短法这一专题的教学，学生不仅掌握了全等三角形的性质和判定方法，还培养了他们的数学思维能力和解决问题的能力。同时，我在教学中注重培养学生的团队协作能力和交流能力，使他们能够在合作中共同成长。总之，本节课的教学案例旨在为学生提供一个实践性强、富有挑战性的学习平台，使他们能够更好地理解和应用全等三角形的知识。
3.引导学生运用数学符号和语言，表达和阐述解题过程和思路。例如，要求学生用数学语言描述全等三角形的判定方法，并解释其原理。
4.鼓励学生积极思考和解决问题，培养他们的自主学习能力和问题解决能力。例如，在解决问题的过程中，引导学生独立思考，寻找解决方案，并进行验证。
（三）小组合作
1.组织学生进行小组讨论和实践活动，培养他们的团队协作能力和交流能力。例如，将学生分成小组，让他们共同解决一个实际问题，要求学生在讨论中交流思路、分享解题方法。
在全等三角形专题课中，学生已经学习了全等三角形的定义、性质和判定方法。通过对全等三角形的性质和判定方法的学习，学生已经能够熟练地运用SSS、SAS、ASA、AAS四种判定方法判断两个三角形是否全等。然而，在解决实际问题时，学生往往需要灵活运用多种方法，而截长补短法作为一种特殊的方法，可以帮助学生更加简洁地解决问题。
3.小组合作培养团队协作能力：组织学生进行小组讨论和实践活动，培养他们的团队协作能力和交流能力。通过小组合作，学生能够在合作中发现问题、解决问题，并培养批判性思维和自我反思能力。
4.反思与评价提高自我认知：教师引导学生对自己的学习过程进行反思，总结经验和教训。通过互评和自我评价，学生能够培养批判性思维和自我反思能力，提高自我认知。
2.引导学生通过观察、分析和归纳，发现全等三角形的性质和判定方法。例如，通过展示两个全等三角形的图形，让学生观察并分析它们的性质，引导学生归纳出全等三角形的判定方法。

几何证明中常用辅助线(一)中线倍长法:例1、求证：三角形一边上的中线小于其他两边和的一半。

已知：如图，△ABC 中，AD 是BC 边上的中线，求证：AD ﹤课堂练习：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线， 求证：∠C=∠BAE 作业：1、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 结论2、已知：如图，?ABC 中，?C=90?，CM ?AB 于M ，AT 平分?BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF （二）截长补短法于点D ，AB +BC =2BD . 求证：∠BAP +∠BCP =180°.分析：与例1相类似，证两个角的和是180°，可把它们移到一起，让它们是邻补角，即证明∠BCP =∠EAP ，因而此题适用“补短”进行全等三角形的构造.DABCMTEC图2-2APN证明：过点P 作PE 垂直BA 的延长线于点E ，如图3-2∵∠1=∠2，且PD ⊥BC ，∴PE =PD ， 在Rt △BPE 与Rt △BPD 中，⎩⎨⎧==BPBP PDPE上述两种方法在实际应用中，时常是互为补充，但应结合具体题目恰当选择合适思路进行分析。

让掌握学生掌握好“截长补短法”对于更好的理解数学中的化归思想有较大的帮助。

作业：1、已知：如图，ABCD 是正方形，∠FAD =∠FAE .求证：BE +DF =AE .2、五边形ABCDE 中，AB =AE ，BC +DE =CD ，∠ABC +∠AED =180°，求证：AD 平分∠CDE F EDCBAC（三）其它几种常见的形式：1、有角平分线时，通常在角的两边截取相等的线段，构造全等三角形。

全等三角形常见辅助线的作法一倍长中线法倍长中线法:就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长××到某点，使什么等于什么（延长的那一条），用SAS证全等（对顶角）方法总结：遇中线，要倍长，倍长之后__构造全等三角形_，转移边、转移角，然后和已知条件重新组合解决问题【例题精讲】例1、如图1，在△ABC中，AD为BC边上的中线．求证：AB+AC＞2AD．分析：①因为AD为中线，延长AD至点E，使DE=AD，连接CE；②进而利用全等三角形的判定（SAS）△ABD≌△ECD；③由全等可得_AB=EC__；证明：延长AD至E，使DE=AD，连接EC∵AD是中线∴DC=DBDC=DB∴△CDE≌△BDA（SAS）∴CE=AB在△AEC中CE+AC>AE，CE=AB∴AB+AC>AE ∵DE=AD∴AE=2AD ∵AB+AC>AE ∴AB+AC>2AD例2如图CB，CD分别是钝角△AEC和锐角△ABC的中线，且AC=AB．求证：CE=2CD．例3、 如图，在ABC ∆中，AD 交BC 于点D ，点E 是BC 中点，EF AD ∥交CA 的延长线于点F ，交EF 于点G ，若BG CF =，求证：AD 为ABC ∆的角平分线．例4、如图，在ABC ∆中，AD 是BC 边的中线，E 是AD 上一点，且BE ＝AC ，延长BE 交AC 于点F ．求证：AF ＝EFBCB C二、截长补短法截长:1.过某一点作长边的垂线 2.在长边上截取一条与某一短边相同的线段，再证剩下的线段与另一短边相等。

补短:1.延长短边 2.通过旋转等方式使两短边拼合到一起。

【例题精讲】例1.如图，△ABC中，∠ACB＝2∠B，∠1＝∠2 求证：AB＝AC＋CD证法一：（补短法）延长AC至点F，使得AF＝AB在△ABD和△AFD中∴△ABD≌△AFD（SAS）∴∠B＝∠F∵∠ACB＝2∠B∴∠ACB＝2∠F而∠ACB＝∠F＋∠FDC∴∠F＝∠FDC∴CD＝CF而AF＝AC＋CF∴AF＝AC＋CD∴AB＝AC＋CD证法二：（截长法）在AB上截取AE＝AC，连结DE在△AED和△ACD中∴△AED≌△ACD（SAS）例2、如图，在△ABC中，AD为BC边上的高，∠B=2∠C.求证：CD=AB+BD.例3、如图，AD//BC ，BE 、AE 分别是∠ABC 、∠BAD 的平分线，点E 在CD 上，求证：AB=AD+BC例4、如图，△ABC 中，AB ＞AC ，AD 是∠BAC 的角平分线，P 是线段AD 上任一点除A 、D 外的任意一点。

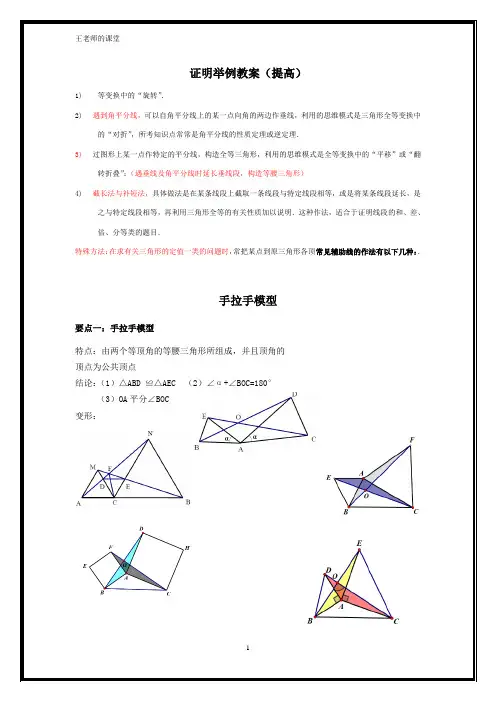
证明举例教案（提高）1)等变换中的“旋转”．2)遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．3)过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”；（遇垂线及角平分线时延长垂线段，构造等腰三角形）4)截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分等类的题目．特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶常见辅助线的作法有以下几种：．手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°（3）OA平分∠BOC变形：例 1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ （2）DC AE =（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2）DC AE =(3）AE 与DC 之间的夹角为︒60(4）AE 与DC 的交点设为H ,BH 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？ （2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？ （4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？ （2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？ （4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ， 问：（1）DBC ABE ∆≅∆是否成立？ （2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？ （4）HB 是否平分AHC ∠？倍长与中点有关的线段倍长中线类☞考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。

《倍长中线法与截长补短法》教学设计教学目标：知识与技能：掌握运用倍长中线法与截长补短法构造全等三角形、解决几何图形问题的方法。

过程与方法：通过学生的自主合作探究，灵活运用倍长中线法与截长补短法解决问题。

情感态度与价值观：通过学生间的合作交流，增强学生的学习信心。

教学重点：倍长中线法与截长补短法的应用。

教学难点：如何运用倍长中线法与截长补短法构造全等三角形解决问题。

教学准备：多媒体课件教学过程：一、问题导入课前互动：同学们，想想我们这段时间学习全等三角形的过程中，遇到的难点是什么呢？（辅助线）课件出示初中几何常见辅助线做法口诀（让学生读，体会其中的含义）问：在三角形中常见的辅助线有哪些？课件展示。

教师引入本节学习内容：倍长中线法与截长补短法（板书课题）二、探究活动，解决问题活动一：倍长中线法在三角形中有中线时，常延长加倍中线，构造全等三角形。

出示例题：已知：如图1，在△ABC中，AD为BC边上的中线．求证：2AD<AB+AC教师引导学生分析解题思路，出示辅助线做法，学生合作解决问题。

课件展示完整解题过程：证明：延长AD至E，使DE=AD,连接CE.∵AD为BC边的中线∴BD=CD在△ADB和△EDC中AD=DE∠ADB=∠EDCBD=CD∴△ADB≌△EDC (SAS)∴AB=CE∵AD+DE<CE+AC∴2AD<AB+AC练习巩固：在△ABC中，分别以AB、AC为直角边向外做等腰直角三角形△ABD和△ACE，F为BC边的中点，FA的延长线与DＥ交于点Ｇ．求证：（１）ＤＥ＝２AF （２）ＦＧ⊥ＤＥ教师引导学生画出辅助线，学生讨论解决问题。

活动二：截长补短法课件出示截长补短法的辅助线做法与应用：要证明两条线段之和等于第三条线段，可以采取“截长补短”法。

截长法即在较长线段上截取一段等于两较短线段中的一条，再证剩下的一段等于另一段线段。

所谓补短，即把两短线段补成一条线段，再证它与长线段相等。

还有一个值得注意的问题是，在总结回顾环节，虽然大部分学生能够跟随我的思路进行复习，但仍有一部分学生显得有些迷茫。这可能是因为他们在课堂上的注意力不够集中，或者是对某些知识点理解不够深入。为了改善这一点，我计划在课后提供一些额外的学习资源，如视频讲解和在线练习，帮助这部分学生巩固知识。
最后，我意识到教学过程中需要不断调整方法和节奏，以适应不同学生的学习需求。在接下来的课程中，我将更加注重个体差异，提供个性化的指导和支持，确保每位学生都能在全等三角形的学习中取得进步。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“全等三角形在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解全等三角形的判定方法及其基本概念。全等三角形是指在大小和形状上完全相同的两个三角形，其判定方法有SSS、SAS、ASA、AAS等。这些判定方法在几何证明和解题中有着重要作用。
2.案例分析：接下来，我们来看一个具体的案例。这个案例展示了如何通过作辅助线，利用全等三角形的判定方法解决实际问题。
3.重点难点解析：在讲授过程中，我会特别强调全等三角形的判定方法和辅助线的常见作法这两个重点。对于难点部分，我会通过具体例题和图形分析来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与全等三角形相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，如利用模型或工具作辅助线，观察全等三角形的形成。

第六讲 全等三角形辅助线之倍长中线与截长补短一、全等三角形知识点复习 1．判定和性质② 全等三角形面积相等． 2．证题的思路：⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧）找任意一边（）找两角的夹边（已知两角）找夹已知边的另一角（）找已知边的对角（）找已知角的另一边（边为角的邻边）任意角（若边为角的对边，则找已知一边一角）找第三边（）找直角（）找夹角（已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS 性质 1、全等三角形的对应角相等、对应边相等。

2、全等三角形的对应边上的高对应相等。

3、全等三角形的对应角平分线相等。

4、全等三角形的对应中线相等。

5、全等三角形面积相等。

6、全等三角形周长相等。

(以上可以简称:全等三角形的对应元素相等) 7、三边对应相等的两个三角形全等。

（SSS)8、两边和它们的夹角对应相等的两个三角形全等。

(SAS) 9、两角和它们的夹边对应相等的两个三角形全等。

(ASA)10、两个角和其中一个角的对边对应相等的两个三角形全等。

(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。

(HL)运用1、性质中三角形全等是条件，结论是对应角、对应边相等。

而全等的判定却刚好相反。

2、利用性质和判定，学会准确地找出两个全等三角形中的对应边与对应角是关键。

在写两个三角形全等时，一定把对应的顶点，角、边的顺序写一致，为找对应边，角提供方便。

3、当图中出现两个以上等边三角形时，应首先考虑用SAS 找全等三角形。

4、用在实际中，一般我们用全等三角形测等距离。

以及等角，用于工业和军事。

有一定帮助。

5、角平分线的性质及判定性质：角平分线上的点到这个角的两边的距离相等 判定：到一个角的两边距离相等的点在这个角平分线上 做题技巧一般来说考试中线段和角相等需要证明全等。

因此我们可以来采取逆思维的方式。

来想要证全等，则需要什么条件另一种则要根据题目中给出的已知条件，求出有关信息。

又∵在△PCM中有：CM>PM-PC(三角形两边之差小于第三边) ∴AB-AC>PB-PC。
A 1 2
P
N
D
B
第13页/共22页
图6 1
C M
在△ABC中，∠ACB=90°，AC=BC,直线MN经过点C， 且AD⊥MN于D，BE⊥MN于E。
求证：DE=AD+BE
证明：∵∠ACB=90°， ∴∠1+∠2=90°. ∵BE⊥MN， ∴∠1+∠3=90°. ∴ ∠2=∠3. ∵AD⊥MN, ∴ ∠ADC= ∠CEB=90°.
截长法即在较长线段上截取一段等于两 较短线段中的一条，再证剩下的一段等于 另一段较短线段。
所谓补短，即把两短线段补成一条，再 证它与长线段相等。
第9页/共22页
让我们来大显身手吧！
例如：已知如图6-1：
在△ABC中，
AB>AC，∠1=∠2，
P为AD上任一点
求证：AB-AC>PB-PC。
N
B
A 1 2
交AE于点F，DF=AC. A
求证：AE平分∠BAC B
提示：
F
D
E
C
第 1 题图
方法1：倍长AE至G，连结DG
方法2：倍长FE至H，连结CH
第5页/共22页
在三角形中线时，常廷长加倍中线，构造全等三角形 。 例如：如图5-1：AD为 △ABC的中线，求证A： AB+AC>2AD
分析：要证AB+AC>2AD，
讲
∵ AD平分∠BAC
2 1
E 3
解
∴ ∠1＝∠2
,
4
B
D
C
在△ABD和 △AED中

12.2 三角形全等的判定（五）基础版【教学目标】1．理解并掌握中线倍长法作辅助线构造全等三角形推导线段数量关系的原理和步骤，熟练解题．2．理解并掌握中线作垂法作辅助线构造全等三角形推导线段数量关系的原理和步骤，熟练解题．3．理解并掌握截长补短法作辅助线构造全等三角形推导线段数量关系的原理和步骤，熟练解题．【重点难点】1．中线倍长法；2．中线作垂法；3．截长补短法．【基本图形】中线倍长法：中线作垂法：重难点1中线倍长法♀例一♀．（△三边关系）如图，已知△ABC中，AB＝4 cm，BC＝6 cm，BD是AC边上的中线，求BD的取值范围．♂巩固练习♂1．求证：三角形一边上的中线小于其他两边和的一半．♀例二♀．（平行线＋角平分线＝等腰△）如图，在四边形ABCD中，AB∥DC，E为BC的中点，△BAE ＝△EAF，AF与DC的延长线交于点F，求证：AF＋CF＝AB．1．如图，CD为△ABC的角平分线，E、F分别在CD、BD上，且DA＝DF，EF＝AC，求证：EF∥BC．2．如图，D为CE的中点，F为AD上一点，且EF＝AC，求证：△DFE＝∠DAC．♀例三♀．如图，AD是△ABC的中线，AE⊥AC，AF⊥AB，且AE＝AC，AF＝AB．求证：AD＝12 EF．1．如图，已知CE、CB分别是△ABC、△ADC的中线，且AB＝AC，△ACB＝△ABC，求证：CD＝2CE．♀例四♀．（1）阅读理解：如图△，在△ABC中，若AB＝10，AC＝6，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E，使DE＝AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中．利用三角形三边关系即可判断中线AD的取值范围是；（2）问题解决：如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE＋CF＞EF；（3）问题拓展：如图③，在四边形ABCD中，∠B＋∠D＝180°，CB＝CD，∠BCD＝140°，以C为顶点作一个70°角，角的两边分别交AB、AD于E、F两点，连接EF，探索线段BE、DF、EF之间的数量关系，并加以证明．①△ △♂巩固练习♂1．如图，在△ABC中，点D是BC中点，点E为AB上一点，DF⊥DE交AC于F，求证：BE＋CF＞EF．♀例五♀．如图，在△ABC中，AD是△A的外角平分线，P是AD上异于A的任意一点．（1）求证：PB＋PC＞AB＋AC；（2）若P是△A的角平分线上一点，且AC＞AB，画出图形，分析PB、PC、AB、AC间又有怎样的不等关系．♂巩固练习♂1．如图，已知△ABC．（1）请你在BC边上分别取两点D、E（BC的中点除外），连接AD、AE，写出使此图中只存在两对面积相等的三角形的相应条件，并表示出面积相等的三角形；（2）请你根据使（1）成立的相应条件，证明：AB＋AC＞AD＋AE．重难点2中线作垂法♀例六♀．如图，△ABC中，D为BC的中点．（1）在图中作出CM⊥AD，BN⊥AD，垂足分别为M、N；（2）求证：DM＝DN；（3）若AD＝3，求AM＋AN的值．♂巩固练习♂1．如图所示，AD是△ABC的中线，E、F分别是AD和AD延长线上的点，且DE＝DF，连接BF、CE．下列说法：△CE＝BF；△△ABD和△ACD面积相等；△BF∥CE；④△BDF≌△CDE．其中正确的有个．2．如图，CD为△ABC的中线，M、N分别为直线CD上的点，且BM∥AN．（1）求证：AN＝BM；（2）求证：CM＋CN＝2CD．♀例七♀．如图，△ABC中，△ABC＝90°，AC＝CE，BC＝CD，△ACE＝△BCD＝90°，BC的延长线交DE于点F．（1）求证：EF＝DF；（2）求证：S△ABC＝S△DCE．♂巩固练习♂1．如图，DA＝DE，△ADE＝90°，C为DE延长线上一点，AB⊥AC，且AB＝AC，延长AD交BE于F．（1）求证：EF＝BF；（2）求DFCE的值．2．如图，△C＝90°，BE⊥AB且BE＝AB，BD⊥BC且BD＝BC，CB的延长线交DE于F．（1）求证：点F是ED的中点；（2）求证：S△ABC＝2S△BEF．重难点3截长补短法♀例八♀．如图，△ABC中，△CAB＝△CBA＝45°，CA＝CB，点E为BC的中点，CN⊥AE交AB于N．（1）求证：△1＝△2；（2）求证：AE＝CN＋EN（请用多种方法证明）（一）直接截长法（2）间接截长法（3）直接补短法（4）间接补短法♂巩固练习♂1．如图，已知在△ABC内，∠BAC＝60°，△C＝40°，P、Q分别在BC、CA上，并且AP、BQ分别是∠BAC，∠ABC的角平分线．求证：BQ＋AQ＝AB＋BP．2．如图，正方形ABCD中，∠GBH的两边分别与直线AD、CD相交于G、H两点，且GH＝AG＋CH，求证：△BEH为等腰直角三角形．。

第11讲 构造全等三角形的方法（2）【学习目标】1． 熟悉并掌握三角形全等的“SSS ”,“ASA ”,“AAS ”,“SAS ”，“HL”条件； 2． 能掌握“倍长中线法”和“截长补短法”。

【学习重点】“倍长中线法”和“截长补短法”的学习。

【学习难点】“倍长中线法”和“截长补短法”的学习，并能对相关题目进行分析方法与技巧的总结与运用。

【知识梳理】1．全等三角形判定方法：(1) “边角边”或“SAS” ；(2) “角边角”或“ASA”；(3) “边边边”或“SSS”；(4) “角角边”或“AAS” ；(5) “斜边、直角边”或“HL” 2．构造全等三角形的方法：（1）通过倍长中线法构造全等三角形；（2）通过截长补短法构造全等三角形。

3．线段的垂直平分线定理：线段垂直平分线上的点，到线段的两端距离相等；4．线段的垂直平分线定理逆定理：到线段两端距离相等的点，在线段垂直平分线上。

5.角平分线定理：角平分线上的点，到角的两边距离相等；6.角平分线定理逆定理：到线段的两端距离相等点，在线段垂直平分线上。

7.等腰三角形三线合一定理：等腰三角形的顶角平分线、底边上的中线和高，三线合一。

【典例剖析】考点一：通过“倍长中线法”构造三角形全等例1：（“希望杯”试题）已知，如图△ABC 中，AB=5，AC=3，则中线AD 的取值范围是 。

例2：（太原中考）△ABC 中, D 为BC 的中点. 过D 点的直线GF 交AC 于F, 交AC 的平行线BG 于点G . DE ⊥GF, 并交AB 于点E. 连结EG ，EF. (1) 求证:BG=CF.(2)请猜想BE+CF 与EF 的大小关系, 并加以证明.例3：（2016黄老培优）以△ABC 的两边AB 、AC 为腰分别向外作等腰Rt △ABD 和等腰Rt △ACE ，∠BAD=∠CAE=90°，连接DE ，M 、N 分别是BC 、DE 的中点．探究：AM 与DE 的位置关系及数量关系． （1）如图① 当△ABC 为直角三角形时，AM 与DE 的位置关系是 ， 线段AM 与DE 的数量关系是 ；（2）将图①中的等腰Rt △ABD 绕点A 沿逆时针方向旋转(090)θθ︒<<后，如图②所示，（1）问中得到的两个结论是否发生改变？并说明理由．例4：如图所示，在△ABC中，AD是∠BAC的角平分线，且AE=AF。

倍长中线与截长补短互动精讲知识点一.倍长中线【知识梳理】∆ABC中AD是BC边中线方式延长AD到E,使DE二AD,连接BE•E方式2：间接倍长，延长MD到N,使DfMD,连接CN作CF丄AD于F,作BE丄AD的延长线于E连接BE【例题精讲】例1、∆ABC 中，AB 二5, AC=3,求中线AD 的取值范围。

.∙. BD= CD I∙.∙ BD = CD t ZADC=ZBDE t AD=DE t ：.AADC 9 ΔEDB t：.EB=AC I 根据三角形的三边关系定理：5-3<∕lE<5 + 3 r .•・ 1 < AD < 4.例2、已知：如图，在ΔABC 中，ABHAC, D 、E 在BC 上，且DE 二EC,过D 作DF//BA 交AE 于点F, DF=AC.求证：AE 平分ZBAC≡ΔPEF 和 ZSCEG 中. ED= EC ZDEF = ZCEG , FE=EG・・^DEF 竺ΔCEG. ∖ DF=GC t ZDFE=ZG. ・• DF // AB l ・.ZDFE=乙BAE. :DF = AC l •・ GC=AC.・.厶G =ECAE..ZBAE=ZCA E .即AE 平分上BAC.{证明：如图，延长FE 到G,使EG=EF ,连接CG.E'：AD 是厶ABC 的中线，【课堂练习】1、在AABC中，AD是BC边上的中线，E是AD上一点，且BE=AC,延长BE交AC于F,求证：AF = EFOCG-AD是BC边上的中线（已知），•・.DC=DB .在厶ADC和AGDB中，'AD=DG< Z4DC-ZGDB(对顶角相等)DC=DBj.^ADC ^GDB(SAS) I:•厶CAD =厶G ■ BG=ACXv BE=AC e・・.BE=BG ,・・・ZBED ZG ,・.・ ZBED= ZAEF t .∖ΛΛEF^= Z.CAD t 即：/.AEF≈ΔFAE t.・・ AF = EF.2、如图，∆ABC中，E、F分别在AB、AC ±, DE丄DF, D是中点，试比较BE+CF 与EF的大小・BE + CF > FP = EF・延长ED 至P , ^DP = DE t连接FP l CP t•・・D是BC的中点，/. BD= CD I在HBDE和ΔCZ)Pφf(DP=DE< 乙EDB=乙CDP[BD=CD・•・ 5BDE ^^CDP(SAS) f.∙. BE=CP l∖∙ DELDF I DE=DP J.∙. EF = FP,(垂直平分线上的点到线段两端点距离相等) 在厶CFP中.CP + CF = BE+ CF > FP = EF・知识点二.截长补短 【知识梳理】截长补短的方法适用于求证线段的和差倍分关系。

“截长补短”全等法教学目标：1、通过观察、操作、归纳等教学活动，积累数学活动经验。

感受数学思维过程的条理性，进一步提高学生的数学思维能力。

2、掌握运用截长补短的方法构造全等三角形，来解决线段的和差问题，体会辅助线在数学中的作用。

3、培养学生积极主动参与学习数学活动的意识，增强学好数学的信心，培养学生与他人合作交流的意识和能力。

教学重点：掌握运用截长补短的方法解决线段的和差问题。

教学难点：正确添加辅助线。

教学流程：一．导入: 开门见山，直接导入新课。

（板书课题）学习完全等三角形的判定之后，往往遇到求证线段相等或角度相等的问题，我们都转化成三角形全等的问题。

但是有的时候并不是让我们证明两条线段相等，而是证明线段之间的和差关系。

遇到这样的问题我们会发现直接证明全等无法完成或比较麻烦，那这样的问题有没有更好的解决办法呢？当然有，这节课我们就一起来探究全等三角形中非常重要的添加辅助线的方法------截长补短全等法。

截长补短是如何在实际问题中应用的呢？下面我们就结合例题研究一下。

二．活动流程：（一）截长补短法1.如图，在△ABC中，∠B＝2∠C，AD平分∠BAC 。

求证：AC=AB+BD.师：直接使用全等，能证出来吗？这时候我们的法宝“截长补短”就发挥作用了。

截长：在长的线段中截取出一条短线段一样长的线段构造出全等三角形，再证明出剩下的线段等于另一条较短的线段。

通过全等完成相等线段的转移。

补短：就是把其中一条较短的线段补成和长的线段同样长的线段，进而得出线段和差关系。

学生动手操作尝试：（1）截长AC上截取AE=AB（2）补短：延长AB至F，使BF=BD,连接FB（3）补短：延长BD至F,使BF=AB,连接AF.（本次活动设置两种解决问题的方法，主要是让学生很容易的想到要一题多解，让学生轻松的进入本节课的课题探究。

）（二）截长法2. 已知：如图，在△ABC 中，∠ABC =60°，△ABC 的角平分线AD ，CE 交于点O ．求证：AC =AE +CD ．（三）补短法3. 已知：如图，在正方形ABCD 中，AD =AB ，∠B =∠D =∠BAD =90°，E ，F 分别为CD ，BC 边上的点，且∠EAF =45°，连接EF ．求证：EF =BF +DE ．4.综合应用： 已知：如图，AE //BC ，AD 、BD 分别是∠EAB 、∠CBA 的平分线，相交于点D ，过点D 的直线EC 交AE 于点E ，交BC 于点C . 求证：AE +BC =AB.三．总结师：无论截长还是补短，都是为了构造全等三角形，进而完成线段和角的转移，得出我们想要的结论，解决问题中到底是选择截长还是补短，这就需要同学们自己去尝试。

研究辅助线作法：在证明几何题目的过程中，常常需要通过全等三角形，研究两条线段（角）的相等关系，或者转移线段或角。

而有些时候，这样的全等三角形在问题中，并不是十分明显，因此，我们有时候，需要通过添加辅助线，构造全等三角形，进而证明所需的结论。

所以做辅助线是有规律可循的三角形中常见辅助线的添加1. 与角平分线有关的（1）可向两边作垂线。

（2）可作平行线，构造等腰三角形（3）在角的两边截取相等的线段，构造全等三角形2. 与线段长度相关的（1）截长：证明某两条线段的和或差等于第三条线段时，经常在较长的线段上截取一段，使得它和其中的一条相等，再利用全等证明余下的等于另一条线段即可（2）补短：证明某两条线段的和或差等于第三条线段时，也可以在较短的线段上延长一段，使得延长的部分等于另外一条较短的线段，再利用全等证明延长后的线段等于那一条长线段即可（3）倍长中线：题目中如果出现了三角形的中线，方法是将中线延长一倍，再将端点连结，便可得到全等三角形。

（4）遇到中点，考虑中位线或等腰等边中的三线合一。

3. 与等腰等边三角形相关的（1）考虑三线合一（2）遇到等腰三角形等边三角形直角三角形，还有一些特殊的做法,比如RT 中，30°角所对的直角边是斜边的一半等（如平谷期末考试24（2））...△ABC 中 AD 是BC边中线方式1：直接倍长中线：方式2：间接倍长（倍长过中点的线段） 延长AD 到E使DE=AD ，作CF ⊥AD 于F ， 作BE ⊥AD 交的AD 的延长线于E连接BE例1△ABC 中，AB=5，AC=3，求中线AD 的取值范围例2已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC于F ，求证：AF=EF提示：延长AD 至G ，连接BG ，证明ΔBDG ≌ΔCDA三角形BEG 是等腰三角形例3已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC.求证：AE 平分BAC ∠提示：方法1：倍长AE 至G ，连结DG方法2：倍长FE 至H ，连结CH例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE 提示：倍长AE 至F ，连结DF证明ΔAB E ≌ΔFDE （SAS ）进而证明ΔADF ≌ΔADC （SAS ） 注：倍长只是方法，做辅助线要说延长---连接---第 1 题图 A B F D E C1、如图，在ABC 中，AC AB >，E 为BC 边的中点，AD 为BAC ∠的平分线，过E 作AD 的平行线，交AB 于F ，交CA 的延长线于G ，求证：BF CG =2、已知如图，ABC 中D 为BC 中点，E 为AC 上一点，AC 与BE 交于点F ，且EA EF =,求证：BF AC =3、如图，CB ，CD 分别是钝角AEC 和锐角ABC 的中线，且AC=AB,求证：CE=2CD总结：“倍长中线”的辅助线包含的基本图形“八字型”和“倍长中线”两种基本操作方法：1、倍长中线，2、倍长过中点的一条线段，对于解决含有过中点线段有很好的效果。

故可在AB上截取AN等于AC
，得AB-AC=BN
再连接PN，则PC=PN，又
N
在△PNB中，PB-PN<BN
即：AB-AC>PB-PC。
B
A 1 2
P C
D
图6 1
M
精选2021版课件
12
证明：（截长法）在AB上截取AN=AC连接PN 在△APN和△APC中
AN=AC（辅助线作法） ∠1=∠2 （已知） AP=AP （公共边） ∴△APN≌△APC （SAS） ∴PC=PN （全等三角形对应边相等） ∵在△BPN中，有 PB-PN<BN （三角形两边之差小于第 三边）
又∵在△PCM中有：CM>PM-PC(三角形两边之差小于第三边) ∴AB-AC>PB-PC。
A 1 2
P
N
D
C
B 精选2021版课件
图6 1
M
14
精选2021版课件
15
左边比要证结论多BD+CD， 故不能直接证出此题， 而由2AD想到要构造2AD，
E 图5 1
即加倍中线，
把所要证的线段转移到同一个三角形中去
精选2021版课件
7
证明：延长AD至E，使DE=AD，连接BE，CE
∵AD为△ABC的中线 （已知）
A
∴BD=CD （中线定义）
在△ACD和△EBD中
BD=CD （已证） ∠1=∠2 （对顶角相等）
E
F
∴∠3+∠2=90° 即：∠EDF=90°
∴∠FDM=∠EDF =90° 在△EDF和△MDF中
12 34
C
B
D
ED= MD （辅助线作 法）