基于多变量时间序列(CAR)模型的 地下水埋深预测

基于时间序列模型的济南趵突泉地下水位预测1 研究背景济南市素有“泉城”的美誉，辖区内分布多处名泉，其中尤以趵突泉最为著名。

而今由于社会经济和城市化进程的不断推进，使得泉水补给区面积骤减，大量新增的硬化面积，削弱了泉域岩溶水的补给量，破坏了区域地下水系统的自然平衡状态，近年来，泉水分布区地下水位的持续下降，使得泉水喷涌受到严重威胁［1-2］。

为了保障泉水的持续喷涌，缓解日益突出的水资源供需矛盾，济南市在启动引黄供水工程的同时充分利用南水北调东线的水源，将外调水与当地地表水相结合，在泉域岩溶水的直接补给区开展回灌补源工程。

随着济南市保泉供水工作陆续开展，王庆兵等［3］设计了4类地下水资源开采方案，运用地下水流数值模型模拟了4种方案对泉群地下水水位及泉水流量动态变化的影响，最终确定泉域地下水可持续开采方案。

高宗军等［4］采用微量元素水文地球化学方法，对济南泉域范围内的丰枯水期岩溶水化学特征及其变化进行调查研究。

邢立亭等［5］采用示踪试验、泉水位动态观测等方法揭示济南岩溶含水介质特征。

张展羽等［6］针对地下水位在时间序列上表现出高度的随机性和滞后性，建立了基于主成分分析与多变量时间序列CAR模型，对泉域内岩溶水水位进行预测。

齐欢等［7］利用地下水数值模拟GMS软件对玉符河补源进行评价，提出西郊水位的抬升可以缓解地下水开采对趵突泉水位的影响，减小保泉的压力。

本文借鉴已有的研究成果，从保泉供水、区域地下水资源保护的角度出发［8］，结合济南泉域岩溶水补给区的水文地质特征和现有的回灌补源工程，利用灰色动态GM（1，1）和时间序列ARIMA、Holt-Winters三种模型分别对趵突泉历年的水位数据进行评价分析，并选择拟合效果最优的模型对泉水位的波动趋势进行预测，为济南市水生态文明建设及泉水资源保护提供依据。

每逢讲到这些故事时，多半别人都是站在女的一面，说那男子都是念书念坏了，一看了那不识字的又不是女学生之类就生气。

Data Base Technique •数据库技术Electronic Technology & Software Engineering 电子技术与软件工程• 121【关键词】时间序列模型 二次平滑法 反证法我们根据我国2012-2016年水资源公报分析我国水资源开发利用现状及存在的主要问题，通过比较和国家提出的2020年2030年目标的偏差进行对比分析，以便对水资源问题进一步分析，也为后期的预测奠定了基础。

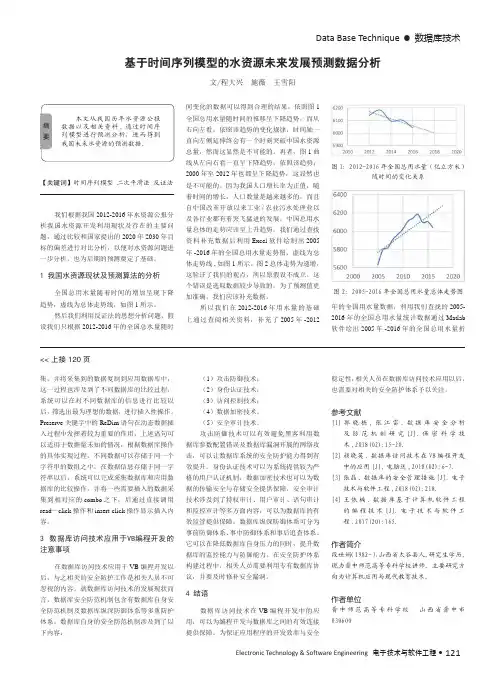
1 我国水资源现状及预测算法的分析全国总用水量随着时间的增加呈现下降趋势，虚线为总体走势线，如图1 所示。

然后我们利用反证法的思想分析问题，假设我们只根据2012-2016年的全国总水量随时基于时间序列模型的水资源未来发展预测数据分析文/程大兴 施薇 王雪阳间变化的数据可以得到合理的结果，依照图1全国总用水量随时间的推移呈下降趋势，而从右向左看，依照该趋势的变化规律，时间轴一直向左侧延伸终会有一个时刻突破中国水资源总量，然而这显然是不可能的。

再者，图1曲线从左向右看一直呈下降趋势，依照该趋势，2000年至2012年也都呈下降趋势，这显然也是不可能的。

因为我国人口增长率为正值，随着时间的增长，人口数量是越来越多的，而且自中国改革开放以来工业/农业污水处理业以及各行业都有着突飞猛进的发展，中国总用水量总体的走势应该呈上升趋势。

我们通过查找资料补充数据后利用Excel 软件绘制出2005年-2016年的全国总用水量走势图，虚线为总体走势线,如图1所示。

图2总体走势为递增，这验证了我们的观点，所以原假设不成立。

这个错误是选取数据较少导致的。

为了预测值更加准确，我们应该补充数据。

所以我们在2012-2016年用水量的基础上通过查阅相关资料，补充了2005年-2012年的全国用水量数据，利用我们查找的2005-2016年的全国总用水量统计数据通过Matlab 软件绘出2005年-2016年的全国总用水量折集，并将采集到的数据复制到应用数据库中，这一过程也涉及到了不同数据库的比较过程，系统可以在对不同数据库的信息进行比较以后，筛选出最为理想的数据，进行插入性操作。

地下水位预测的数学建模与优化随着城市化的发展，水资源的供需问题日益严重。

在这个背景下，地下水资源的管理变得越发重要。

而地下水位预测作为一个基本工具，被广泛地应用于地下水的管理。

然而，为了提高地下水位预测的精度和有效性，数学建模与优化显得尤为必要。

1. 地下水位预测的数学建模地下水位预测是通过建立地下水位与时间和空间的关系来实现的。

在这个过程中，数学建模扮演着不可或缺的角色。

具体来说，数学建模需要考虑以下几个方面：1.1 地下水位变化的原因地下水位的变化由多种因素共同作用而成。

比如气象条件、地质条件、人类活动等。

因此，建立一个合理的模型需要考虑到这些因素。

1.2 模型的变量和参数Modeling a groundwater system requires selecting relevant variables such as hydraulic head, groundwater recharge, and aquifer properties (transmissivity and storage coefficient) as well as relevant parameters such as evapotranspiration rates and recharge from surface streams.1.3 模型的数学表达式通过考虑以上因素和变量来建立数学模型。

其中，变量需要通过实测数据获取，而参数则需要通过拟合实际数据来获取。

然后，模型可以作为数学方程来表示。

例如，流量平衡方程、传递方程等。

2. 地下水位预测的数学优化建立合适的数学模型是地下水位预测的前提，但是模型本身并不能保证预测的精度。

因此，数学优化是提高预测精度的关键。

2.1 优化模型参数模型参数的选择有重要的影响了地下水位预测的质量。

因此，通过对实测数据的拟合来优化模型参数可以使预测结果更准确。

拟合数据的方法包括回归分析、最小二乘法等。

基于时间序列的水污染预测与解决方案第一章：引言水是人类生存和发展的基础，然而水污染问题却日益严重。

为了解决水污染问题以及预防水污染的发生，许多研究人员开始采用基于时间序列的方法来预测水污染，并提出相应的解决方案。

本文将探讨基于时间序列的水污染预测方法及其解决方案，旨在提供对该领域的深入了解和启发。

第二章：时间序列分析时间序列分析是一种统计学方法，用于确定和预测时间序列数据中的趋势和周期性变化。

在水污染预测中，时间序列分析可以帮助我们理解水污染的变化趋势和周期性，从而识别潜在的污染源和制定针对性的措施。

第三章：水污染预测模型3.1 自回归移动平均模型（ARMA）ARMA模型是一种广泛应用于时间序列分析的模型。

它结合了自回归（AR）模型和移动平均（MA）模型，用于描述时间序列中的线性依赖关系。

在水污染预测中，ARMA模型可以根据历史数据预测未来的水污染情况，从而帮助我们采取相应的防治措施。

3.2 自回归积分滑动平均模型（ARIMA）ARIMA模型是ARMA模型的扩展，它引入了差分操作，能够处理非平稳的时间序列数据。

在水污染预测中，ARIMA模型可以帮助我们分析水污染数据的趋势和季节性变化，并预测未来的水污染状况。

3.3 基于神经网络的时间序列模型神经网络是一种模拟人脑神经元之间相互连接的数学模型，被广泛应用于时间序列分析和预测。

在水污染预测中，基于神经网络的时间序列模型可以通过学习历史数据的模式和规律，准确地预测未来的水污染情况。

第四章：水污染解决方案4.1 持续监测与评估为了有效解决水污染问题，我们需要建立持续监测和评估机制。

通过使用传感器和监测设备，我们可以实时收集水质数据，并对其进行分析和评估。

这有助于我们及时发现水污染问题，并采取相应的措施进行治理。

4.2 污水处理与资源化利用污水处理是解决水污染问题的重要环节。

采用适当的污水处理技术，可以有效去除水中的污染物，提高水质。

同时，资源化利用污水中的有价值物质也是一种可持续的解决方案，可以减少对自然资源的依赖。

地下水位预测与管理技术研究地下水是地球上不可或缺的水资源之一，为城市建设、农业灌溉、生态环境等领域提供了重要的保障。

然而，随着经济社会的快速发展，地下水资源面临着日益严重的过度开采和污染问题，导致地下水位下降、水质变差等一系列环境问题。

为了更好地管理和利用地下水资源，预测地下水位变化成为了研究的一个重要方向。

地下水位预测技术主要有以下几种：一、统计模型预测法统计模型预测法是利用历史地下水位资料对未来地下水位进行预测的方法，一般采取时序分析的方法建立预测模型。

时序分析包括自回归模型、移动平均模型、ARIMA模型等。

这类模型主要适用于数据量充足、变化规律稳定的地区，预测精度相对较高。

二、水文地质模型预测法水文地质模型预测法是利用地下水水文地质特征，运用数学模型对地下水位进行预测的方法。

这类模型包括水文地质模型、计算机模拟模型等。

通过模拟地下水的流动和输运过程，对地下水位进行精确预测，适用于地下水水文地质条件较为复杂的地区。

三、遥感与GIS技术预测法遥感与GIS技术预测法主要是利用遥感图像和地理信息系统对地下水位进行预测，这种方法基于遥感数据分析、统计分析和时间序列方法，是一种较为先进的地下水位预测方法。

此外，还可借助人工神经网络、支持向量机等算法以提高预测精度。

对于地下水位管理，主要包括以下几个方面：一、加强地下水位监测地下水位监测是管理地下水的基础，只有了解地下水位变化的情况，才能采取有效的管理措施。

因此，必须加强地下水位监测站的建设，完善地下水位监测网络，实时掌握地下水位的变化情况。

同时，还应建立地下水位数据中心，对监测数据进行统计、分析和预测，提高地下水位管理的科学性和精确性。

二、坚持节约用水节约用水是防止地下水位下降的重要措施之一。

我国已经实施了“三定”政策（即定人、定额、定价），对城镇居民用水进行配额管理，并加强水资源的回用和再利用。

此外，还应推广水资源高效利用技术，如雨水收集、灌溉技术改造等，以减少用水量。

三种地下水位动态预测模型在吉林西部的应用与对比地下水位预测是水资源管理和灾害防治领域中的重要问题。

在吉林西部地区的地下水位预测中，常常使用的三种模型有ARIMA模型、BP神经网络模型和支持向量回归模型。

本文将分别介绍这三种模型的原理和应用，并进行比较。

ARIMA模型是一种常用的时间序列分析方法，可以对时间序列数据进行拟合和预测。

在地下水位预测中，可以将历史地下水位数据看作时间序列数据，使用ARIMA模型对其进行建模和预测。

ARIMA模型通过分析时间序列的自相关性、差分和移动平均等特征，预测未来地下水位的变化趋势。

ARIMA模型在吉林西部地下水位预测中具有较好的稳定性和准确性。

BP神经网络模型是一种基于人工神经网络的预测模型，可以通过训练神经网络来学习地下水位的变化规律，并用于未来地下水位的预测。

BP神经网络模型具有自适应性和非线性拟合能力，可以处理各种复杂的地下水位预测问题。

在吉林西部地下水位预测中，BP神经网络模型可以根据历史地下水位数据和其他影响因素进行训练和预测，能够较好地模拟地下水位的动态变化。

支持向量回归模型是一种基于统计学习理论的预测模型，可以通过构建高维特征空间和最优超平面来预测地下水位的变化。

支持向量回归模型在吉林西部地下水位预测中的应用较少，但具有较好的泛化性能和鲁棒性。

支持向量回归模型可以根据历史地下水位数据和其他相关变量进行训练和预测，能够提供较为准确的地下水位预测结果。

对比来看，ARIMA模型适用于相对简单的地下水位预测问题，具有较好的稳定性和准确性；BP神经网络模型适用于复杂的地下水位预测问题，具有强大的非线性拟合能力；支持向量回归模型适用于需要考虑多个变量和复杂关系的地下水位预测问题。

综上所述，根据地下水位预测的具体情况和要求，可以选择适合的模型进行应用。

在吉林西部地下水位预测中，ARIMA模型、BP神经网络模型和支持向量回归模型都具有一定的应用潜力，可以根据具体情况选择合适的模型进行预测。