第9章-假设检验答案

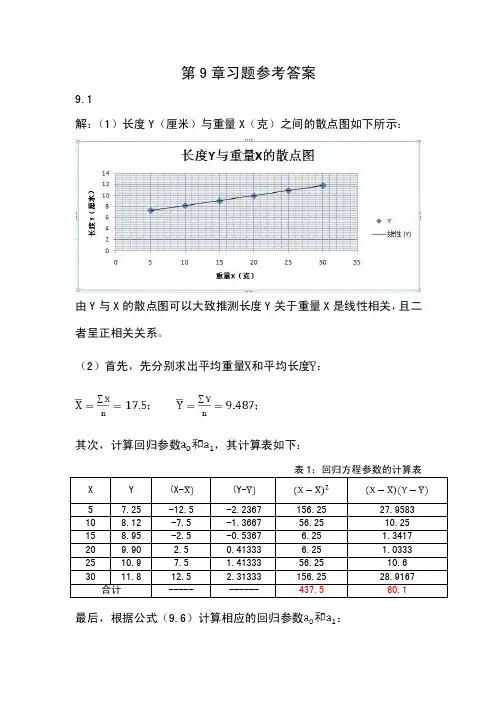
第9章习题参考答案
9.1
解：（1）长度Y（厘米）与重量X（克）之间的散点图如下所示：
由Y与X的散点图可以大致推测长度Y关于重量X是线性相关，且二者呈正相关关系。

（2）首先，先分别求出平均重量和平均长度：
；；
其次，计算回归参数，其计算表如下：
表1：回归方程参数的计算表
(X-(Y-
最后，根据公式（9.6）计算相应的回归参数：
；
所以，Y关于X的一元线性回归方程为：
9.5
解：总变差，回归平方和，残差平方和的计算如下：
表2：总变差，回归平方和，残差平方和的计算表
∴残差平方和：；
回归平方和：
9.6
解：由表2得：
判定系数
又∵习题9.1的散点图显示Y与X是呈正相关关系
∴相关系数
显著性检验：
（1）回归方程的显著性检验：
原假设H0：该回归方程不显著；备择假设H1：该回归方程显著
计算F统计量：
∵在α=0.05的显著性水平下，有4454.79＞F0.05(1,4)=7.71
∴拒绝原假设，认为该回归方程式显著的。

（2）回归参数的假设检验：
原假设H0：备择假设H1：
计算t统计量：;
[其中] ∵在α=0.05的显著性水平下，有15.98＞t0.05（4）=2.776
∴拒绝原假设，即认为自变量X对因变量Y有显著性影响。

(3)相关关系的显著性检验：
原假设H0：ρ=0；备择假设H1：ρ
计算t统计量：；
∵在α=0.05的显著性水平下，有66.64> t0.05（4）=2.776
∴拒绝原假设，认为总体相关系数不为0。

生物统计学习题答案第九章第九章生物统计学习题答案第一节：描述统计学习题答案1. 样本的均值是样本观测值的算术平均数。

计算样本均值的方法是将所有观测值相加，然后除以样本的大小。

2. 样本的中位数是将样本观测值按照大小排序，然后找出中间位置的观测值。

如果样本的大小为奇数，中位数就是排序后的中间值；如果样本的大小为偶数，中位数就是排序后中间两个值的平均数。

3. 样本的众数是样本中出现次数最多的观测值。

一个样本可以有一个或多个众数，也可以没有众数。

4. 样本的范围是最大观测值与最小观测值之间的差异。

计算样本范围的方法是将最大观测值减去最小观测值。

5. 样本的方差是观测值与样本均值之间的差异的平方的平均数。

计算样本方差的方法是将每个观测值与样本均值之间的差异平方，然后将所有差异平方相加，最后除以样本的大小减一。

6. 样本的标准差是样本方差的平方根。

计算样本标准差的方法是将样本方差的结果开根号。

第二节：推断统计学习题答案1. 置信区间是用来估计总体参数的范围。

置信区间的计算方法是使用样本统计量和置信水平来计算。

2. 假设检验是用来判断总体参数是否等于某个特定值的方法。

假设检验的步骤包括建立原假设和备择假设、选择适当的检验统计量、计算观测值的p值、根据p值来判断是否拒绝原假设。

3. 单样本t检验是用来比较一个样本的均值与总体均值之间是否存在显著差异的方法。

单样本t检验的步骤包括建立原假设和备择假设、计算t值、计算p 值、根据p值来判断是否拒绝原假设。

4. 独立样本t检验是用来比较两个独立样本的均值是否存在显著差异的方法。

独立样本t检验的步骤包括建立原假设和备择假设、计算t值、计算p值、根据p值来判断是否拒绝原假设。

5. 配对样本t检验是用来比较同一组样本在两个不同时间点或条件下的均值是否存在显著差异的方法。

配对样本t检验的步骤包括建立原假设和备择假设、计算差异值、计算差异值的均值和标准差、计算t值、计算p值、根据p值来判断是否拒绝原假设。

第七章 假设检验与方差分析 习题答案一、名词解释用规范性的语言解释统计学中的名词。

1. 假设检验：对总体分布或参数做出某种假设，然后再依据抽取的样本信息，对假设是否正确做出统计判断，即是否拒绝这种假设。

2. 原假设：又叫零假设或无效假设，是待检验的假设，表示为 H 0，总是含有等号。

3. 备择假设：是零假设的对立，表示为 H 1，总是含有不等号。

4. 单侧检验：备择假设符号为大于或小于时的假设检验。

5. 显著性水平：原假设为真时，拒绝原假设的概率。

6. 方差分析：是检验多个总体均值是否相等的一种统计分析方法。

二、判断改错对下列命题进行判断，在正确命题的括号内打“√”；在错误命题的括号内打“×”，并在错误的地方下划一横线，将改正后的内容写入题下空白处。

1. 在任何情况下，假设检验中的两类错误都不可能同时降低。

( × ) 样本量一定时2. 对于两样本的均值检验问题，若方差均未知，则方差分析和t 检验均可使用，且两者检验结果一致。

( √ )3. 方差分析中，组间离差平方和总是大于组内离差平方和。

( × )不一定4. 在假设检验中，如果在显著性水平0.05下拒绝了00:μμ≤H ，则在同一水平一定可以拒绝假设00:μμ=H 。

( × )不一定5. 为检验k 个总体均值是否显著不同，也可以用t 检验，且与方差分析相比，犯第一类错误的概率不变。

（ × ）会增加6. 方差分析中，若拒绝了零假设，则认为各个总体均值均有显著性差异。

( × ) 不完全相等六、简答题根据题意，用简明扼要的语言回答问题。

1. 假设检验与统计估计有何区别与联系？【答题要点】假设检验是在给定显著性水平下，计算出拒绝域，并根据样本统计量信息来做出是否拒绝零假设的决策；区间估计是利用样本信息来推断总体参数的一个可能范围。

区间估计结果可以用于假设检验，但假设检验不能用作区间估计。

2. 双侧检验与单侧检验有什么区别？【答题要点】双侧检验的零假设为等号，备择假设为不等号，得到的拒绝域为双侧的；单侧检验的备择假设或者是大于，或者是小于，其拒绝域为单侧区间。

假设检验考试试题及答案解析一、单选题（本大题9小题．每题1.0分，共9.0分。

请从以下每一道考题下面备选答案中选择一个最佳答案，并在答题卡上将相应题号的相应字母所属的方框涂黑。

）第1题假设检验中的显著性水平α是( )。

A 推断时犯第Ⅱ类错误的概率B 推断时犯第Ⅰ和第Ⅱ类错误的概率C 推断时犯第Ⅰ类错误的概率D 推断时犯第Ⅲ类错误的概率【正确答案】：C【本题分数】：1.0分【答案解析】[解析] 显著性水平α是犯第Ⅰ类错误的概率，也就是原假设H0为真，却拒绝H的概率。

第2题当总体服从正态分布，但总体方差未知的情况下，H0:μ=μ，H1:μ＜μ则H的拒绝域为( )。

A t≤tα(n-1)B t≤-tα(n-1)C t＞-tα(n-1)D t≤(n-1)【正确答案】：B【本题分数】：1.0分第3题从一批零件中抽出100个测量其直径，测得平均直径为5.2cm，标准差为1.6cm，想知道这批零件的直径是否服从标准直径5cm，因此采用t检验法，那么在显著性水平α下，接受域为( )。

模考吧网提供最优质的模拟试题，最全的历年真题，最精准的预测押题！A |t|≥tα/2(99)B |t|＜tα/2(100)C |t|＜tα/2(99)D |t|≤tα/2(99)【正确答案】：C【本题分数】：1.0分【答案解析】[解析] 采用t检验法进行双边检验时，因为，所以在显著性水平α下，接受域为|t|≤tα/2(99)。

第4题在假设检验中，若抽样单位数不变，显著性水平从0.01提高到0.1，则犯第二类错误的概率( )。

A 也将提高B 不变C 将会下降D 可能提高，也可能不变【正确答案】：C【本题分数】：1.0分【答案解析】[解析] 原假设H0非真时作出接受H的选择，这种错误称为第二类错误。

在一定样本容量下，减少α会引起β增大，减少β会引起α的增大。

第5题机床厂某日从两台机器所加工的同一种零件中，分别抽取两个样本，检验两台机床的加工精度是否相同，则提出假设( )。

一、单选题1、在假设检验中，我们认为（）。

A.原假设是不容置疑的B.拒绝域总是位于检验统计量分布的两边C.小概率事件在一次抽样中实际上不会发生D.检验统计量落入拒绝域是不可能的正确答案：C2、在假设检验中，显著性水平确定后（）。

A.双边检验的拒绝域小于单边检验的拒绝域B.双边检验的拒绝域大于单边检验的拒绝域C.双边检验的拒绝域与单边检验的拒绝域不可简单直接对比D.双边检验的拒绝域等于单边检验的拒绝域正确答案：C3、单个正态总体均值的检验时若总体方差已知，（）。

A.设计的检验统计量服从卡方分布B.设计的检验统计量服从F分布C.设计的检验统计量服从标准正态分布D.设计的检验统计量服从t分布正确答案：C4、总体成数的假设检验（）。

A.设计的检验统计量服从标准正态分布B.设计的检验统计量服从卡方分布C.设计的检验统计量近似服从卡方分布D.设计的检验统计量近似服从标准正态分布正确答案：D5、两个正态总体均值之差的检验中，如果两个总体方差未知但相等，检验统计量t的自由度是（）。

A.两样本容量之和B.两样本容量之和减2C.两样本容量之积D.两样本容量之和减1正确答案：B6、假设检验是检验（）的假设值是否成立。

A.总体均值B.总体指标C.样本方差D.样本指标正确答案：B7、在大样本条件下，样本成数的抽样分布近似为（）。

A.均匀分布B.卡方分布C.二项分布D.正态分布正确答案：D8、下列关于假设检验的说法，不正确的是（）。

A.作出“拒绝原假设”决策时可能会犯第一类错误B.作出“不能拒绝原假设”决策时意味着原假设正确C.作出“不能拒绝原假设”决策时可能会犯第二类错误D.作出“接受原假设”决策时意味着没有充分的理由认为原假设是错误的正确答案：B9、将由显著性水平所规定的拒绝域平分为两部分，置于概率分布的两，每边占显著性水平的二分之一，这是（）。

A.右侧检验B.单侧检验C.左侧检验D.双侧检验正确答案：D10、如果使用者偏重于担心出现纳伪错误而造成的损失，则应把显著性水平定得（）。

贾俊平的《统计学》是一本经典的统计学优秀教材。作为该教材的学习辅导书，本书具 有以下几个方面的特点：
1．针对性强，解决难点。精选人大、中央财大等名校统计学院的初试和复试的考研真 题，既注重基础知识的掌握，又对一些难题、易错题目给出了详细的解析。本书特别适用于 参加研究生入学考试和复试指定考研参考书目为贾俊平主编的《统计学》的考生。
要深深牢记：考研不同一般考试，概念题（名词解释）要当作简答题来回答，简答题要 当作论述题来解答，而论述题的答案要像是论文，多答不扣分。有的论述题的答案简直就是 一份优秀的论文（其实很多考研真题就是选自一篇专题论文），完全需要当作论文来回答！
统计类国内外经典教材习题详解系列是一套全面解析统计类国内外经典教材的辅导资 料。贾俊平的《统计学》、袁卫的《统计学》是国内最受欢迎的统计学经典教材。本书是各 个高校基础专业课统计学考研真题（含复试）与典型题详解，是参考统计学权威教材、全国 各大院校统计学考卷的结构和内容、统计硕士考试大纲、同等学力人员申请硕士学位试题来
2．题量充足，来源广泛。主要选自 40 余所高校的历年考研真题、名校题库以及参考 众多教材和相关资料改编而成。可以说本书的试题都经过了精心挑选，博选众书，取长补短。
3．解答详尽，条理清晰。本书所选部分考研真题有相当的难度，对每道题都尽可能给 出详细的参考答案，条理分明，便于理解。
需要特别说明的是：有些考题的时间较早或内容有点过时，但很值得参考，不失为优秀 考题，因此仍然选用。我们深深感谢贾俊平教授和中国人民大学出版社为我们提供了这样一 本优秀的统计学教材。
贾俊平《统计学》课后习题答案在线阅读：https:///cUb7v8DC
A．品质标志 B．数量标志 C．标志值 D．数量指标 【答案】A 【解析】“等级”属于分类型数据，只能用文字来描述，因此是品质标志，其标志值为“优 秀”“良好”“及格”。 4 下面不属于描述统计问题的是（ ）。[山东大学 2015 研] A．根据样本信息对总体进行的推断 B．了解数据分布的特征顺序数据 C．分析感兴趣的总体特征 D．利用图、表或其他数据汇总工具分析数据 【答案】A 【解析】描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。 BCD 三项都是描述统计问题。A 项中根据样本信息对总体进行推断则是推断统计内容。 5 一项民意调查的目的是想确定年轻人愿意与其父母讨论的话题。调查结果表明：45%的年 轻人愿意与其父母讨论家庭财务状况，38%的年轻人愿意与其父母讨论有关教育的话题， 15%的年轻人愿意与其父母讨论爱情问题。该调查所收集的数据是（ ）。[山东大学 2015 研] A．分类数据 B．顺序数据 C．数值型数据

医学统计学第六版(马斌荣)课后习题答案第一章绪论部分一、单项选择题答案 1. D 2. E 3. D 4. B 5. A 6. D 7. A 8. C 9. E 10. D二、简答题1答由样本数据获得的结果，需要对其进行统计描述和统计推断，统计描述可以使数据更容易理解，统计推断则可以使用概率的方式给出结论，两者的重要作用在于能够透过偶然现象来探测具有变异性的医学规律，使研究结论具有科学性。

2答医学统计学的基本内容包括统计设计、数据整理、统计描述和统计推断。

统计设计能够提高研究效率，并使结果更加准确和可靠，数据整理主要是对数据进行归类，检查数据质量，以及是否符合特定的统计分析方法要求等。

统计描述用来描述及总结数据的重要特征，统计推断指由样本数据的特征推断总体特征的方法，包括参数估计和假设检验。

3答统计描述结果的表达方式主要是通过统计指标、统计表和统计图，统计推断主要是计算参数估计的可信区间、假设检验的P 值得出相互比较是否有差别的结论。

4答统计量是描述样本特征的指标，由样本数据计算得到，参数是描述总体分布特征的指标可由“全体”数据算出。

5答系统误差、随机测量误差、抽样误差。

系统误差由一些固定因素产生，随机测量误差是生物体的自然变异和各种不可预知因素产生的误差，抽样误差是由于抽样而引起的样本统计量与总体参数间的差异。

6答三个总体一是“心肌梗死患者”所属的总体二是接受尿激酶原治疗患者所属的总体三是接受瑞替普酶治疗患者所在的总体。

第二章定量数据的统计描述一、单项选择题答案 1. A 2. B 3. E 4. B 5. A 6. E 7. E 8. D 9. B 10. E二、计算与分析2第三章正态分布与医学参考值范围一、单项选择题答案 1. A 2. B 3. B 4. C 5. D 6. D 7. C 8. E 9. B 10. A二、计算与分析12[参考答案] 题中所给资料属于正偏态分布资料，所以宜用百分位数法计算其参考值范围。

假设检验练习题1. 简单回答下列问题：1假设检验的基本步骤答：第一步建立假设通常建立两个假设;原假设H0 不需证明的命题;一般是相等、无差别的结论;备择假设H1;与H0对立的命题;一般是不相等;有差别的结论有三类假设第二步选择检验统计量给出拒绝域的形式..根据原假设的参数检验统计量：对于给定的显著水平样本空间可分为两部分：拒绝域W 非拒绝域A拒绝域的形式由备择假设的形式决定H1：W为双边H1：W为单边H1：W为单边第三步：给出假设检验的显著水平第四步给出零界值C;确定拒绝域W有了显著水平按照统计量的分布可查表得到临界值;确定拒绝域..例如：对于=0.05有的双边W为的右单边W为的右单边W为第五步根据样本观测值;计算和判断计算统计量Z 、t 、当检验统计量的值落在W内时能拒绝; 否则接受计算P值227页p值由统计软件直接得出时拒绝;否则接受计算1-a的置信区间置信区间由统计软件直接得出统计量落入置信区间接受;否则接受2假设检验的两类错误及其发生的概率答：第一类错误：当为真时拒绝;发生的概率为第二类错误：当为假时;接受发生的概率为3假设检验结果判定的3种方式答：1.计算统计量Z 、t 、当检验统计量的值落在W内时能拒绝; 否则接受2.计算P值227页p值由统计软件直接得出时拒绝;否则接受3.计算1-a的置信区间置信区间由统计软件直接得出;落入置信区间接受;否则接受4在六西格玛A阶段常用的假设检验有那几种应用的对象是什么答：连续型测量的数据：单样本t检验-----比较目标均值双样本t检验-----比较两个均值方差分析-----比较两个以上均值等方差检验-----比较多个方差离散型区分或数的数据：卡方检验-----比较离散数2．设某种产品的指标服从正态分布;它的标准差σ=150;今抽取一个容量为26 的样本;计算得平均值为1 637..问在5%的显著水平下;能否认为这批产品的指标的期望值μ = 1600..答：典型的Z检验1. 提出原假设和备择假设：平均值等于1600 ：平均值不等于16002. 检验统计量为Z;拒绝域为双边~~N0;13.4. 查表得5. 计算统计量Z;有1.26=1.26<1.96 Z未落入拒绝域不能拒绝;目前能认为这批产品的指标的期望值μ = 1600..3．从正态总体Nμ ;1中抽取100 个样品;计算得 = 5.32..试检验:XH0 : μ = 5是否成立α = 0.05 ..答：典型的Z检验1. 提出原假设和备择假设：μ = 5：μ不等于52. 检验统计量为Z;拒绝域为双边~~N0;13.4. 查表得5. 计算统计量Z;有3.2=3.2 1.96 Z落入拒绝域拒绝;目前能认为这批产品的指标的期望值μ不等于5..4．根据资料用某种旧安眠药时;平均睡眠时间为20.8 h;标准差为1.6 h..有一种新安眠药;据说在一定剂量下;能比旧安眠药平均增加睡眠时间3 h..为了检验这个说法是否正确;收集到一组使用新安眠药的睡眠时间单位：h为：26.7;22.0;24.1;21.0;27.2;25.0;23.4..试问：从这组数据能否说明新安眠药已达到新的疗效假定睡眠时间服从正态分布;α = 0.05 ..答：分析：未知;假设检验中的t检验第一步提出原假设和备择假设=23.8 23.8第二步检验统计量为t;拒绝域为双边~~t5第三、四步：时查表得第五步：计算统计量t;有=0.46t=0.46<2.571 t未落入拒绝域接受;此新安眠药已达到新的疗效.5．测定某种溶液中的水份;由其10 个测定值求得= 0.452%; s = 0.037%;设X测定值总体服从正态分布Nμ ;σ2 ;试在显著水平α = 0.05 下;分别检验假设：1 H0: μ = 0.5% ；2 H0: σ = 0.04% ..6．有甲、乙两台机床加工同样产品;从这两台机床加工的产品中随机抽取若干件;测得产品直径单位：mm为机车甲 20.5 19.8 19.7 20.4 20.1 20.0 19.0 19.9机车乙 19.7 20.8 20.5 19.8 19.4 20.6 19.2假定两台机床加工的产品的直径都服从正态分布;且总体方差相等;试比较甲、乙两台机床加工的产品的直径有无显著差异α = 0.05 ..7．测得两批电子器件的样品的电阻单位：Ω为A 批： 0.140 0.138 0.143 0.142 0.144 0.137B 批： 0.135 0.140 0.142 0.138 0.136 0.140设这两批器材的电阻值总体分别服从分布N μ12 ;σ12 ;Nμ22 ;σ22 ;且两样本独立..1 检验假设H0: σ12 =σ22取α = 0.05 ；2 在1的基础上检验H 0 :μ1 = μ2取α = 0.05 ..8.对吸烟者生肺病的情况作过调查;数据如下:试问：生肺病与吸烟是否有关9. 根据某地环境保护的规定;倾入河流的废水中一种有毒化学物质的平均含量不得超过3ppm..已知废水中该有毒化学物质的含量X服从正态分布..该地区环保组织对沿涸一工厂进行检查;测定其每天倾入河流废水中该有毒物质的含量;15天的数据如下单位为ppm：3.1;3.2;3.3;2.9;3.5;3.4;2.5;4.3;2.9;3.6;3.2;3.0;2.7;3.5;2.9..试在α = 0.05的水平上判断该工厂的排放是否符合环保规定答：分析：未知;假设检验中的t检验第一步提出原假设和备择假设第二步检验统计量为t;拒绝域为单边~~t7第三、四步：时查表得第五步：计算统计量t;有=9.77未落入拒绝域接受10. 用三台机器生产规格相同的铝合金薄板;取样测量铝合金薄板的厚度结果如下：机器1 机器2 机器30.236 0.257 0.2580.238 0.253 0.2640.248 0.255 0.259我们假定影响铝合金薄板厚度的因素除机器之外其它的因素都相同;试判断机器对铝合金薄板的厚度是否有显著影响..练习题答案1．略2．接受H03.拒绝H04．新安眠药已达到新的疗效..5．1拒绝H0；2接受H0 ..6直径无显著差异..7．1 接受H0；2接受H0 ..8. 有关系;p＝0.022..9. 不符合环保规定..10.有影响。

1．假设某产品的重量服从正态分布，现在从一批产品中随机抽取16件，测得平均重量为820克，标准差为60克，试以显著性水平α=0.01与α=0.05，分别检验这批产品的平均重量是否是800克。

解：假设检验为800:,800:0100≠=μμH H (产品重量应该使用双侧 检验)。

采用t 分布的检验统计量nx t /0σμ-=。

查出α＝0.05和0.01两个水平下的临界值(df=n-1=15)为2.131和2.947。

667.116/60800820=-=t 。

因为t <2.131<2.947，所以在两个水平下都接受原假设。

2．某牌号彩电规定无故障时间为10 000小时，厂家采取改进措施，现在从新批量彩电中抽取100台，测得平均无故障时间为10 150小时，标准差为500小时，能否据此判断该彩电无故障时间有显著增加(α=0.01)？解：假设检验为10000:,10000:0100>=μμH H （使用寿命有无显著增加，应该使用右侧检验）。

n=100可近似采用正态分布的检验统计量nx z /0σμ-=。

查出α＝0.01水平下的反查正态概率表得到临界值2.32到2.34之间（因为表中给出的是双侧检验的接受域临界值，因此本题的单侧检验显著性水平应先乘以2，再查到对应的临界值）。

计算统计量值3100/5001000010150=-=z 。

因为z=3>2.34(>2.32)，所以拒绝原假设，无故障时间有显著增加。

3.设某产品的指标服从正态分布，它的标准差σ已知为150，今抽了一个容量为26的样本，计算得平均值为1637。

问在5％的显著水平下，能否认为这批产品的指标的期望值μ为1600?解: 01:1600, :1600,H H μμ=≠标准差σ已知,拒绝域为2Z z α>,取0.05,α=26,n =0.0250.9752 1.96z z z α===,由检验统计量1.25 1.96Z ===<,接受0:1600H μ=, 即,以95%的把握认为这批产品的指标的期望值μ为1600.4.某电器零件的平均电阻一直保持在2.64Ω，改变加工工艺后，测得100个零件的平均电阻为2.62Ω，如改变工艺前后电阻的标准差保持在O.06Ω，问新工艺对此零件的电阻有无显著影响(α=0.05)?解: 01: 2.64, : 2.64,H H μμ=≠已知标准差σ=0.16,拒绝域为2Z z α>,取0.02520.05, 1.96z z αα===,100,n =由检验统计量3.33 1.96Z ===>,接受1: 2.64H μ≠, 即, 以95%的把握认为新工艺对此零件的电阻有显著影响.5．某食品厂用自动装罐机装罐头食品，每罐标准重量为500克，每隔一定时间需要检查机器工作情况。

第九章 假设检验(练习及习题标准答案) 一、单项选择题1.当总体服从正态分布，但总体方差未知小样本的情况下，0100:;:μμμμ〈≥H H ，则0H 的拒绝域为( ) A.)1(-≤n t t α B. )1(--≤n t t α C. )1(--〉n t t α D. )1(/2--≤n t t α 2.在假设检验中，原假设0H ，备选假设1H ，则称( )为犯第二类错误。

A.0H 为真，不拒绝1H B. 0H 为真，拒绝1H C. 0H 不真，不拒绝0H D. 0H 不真，拒绝0H 3.假设检验是对未知总体某个特征提出某种假设，而验证假设是否成立的资料是( )。

A.样本资料B.总体全部资料C.重点资料D.典型资料4.下列对总体特征值θ的假设，哪一种写法是正确的?( )。

A. 0100:;:θθθθ〈≥H HB. 0100:;:θθθθ≤≥H HC.0100:;:θθθθ〈≤H HD.0100:;:θθθθ≥=H H 5. 一家食品生产企业声称，它们生产的某种食品的合格率在95%以上。

为检验这一说法是否属实，某食品安全检测部门打算抽取部分食品进行检验，该检验的原假设和备择假设为（ ）A. %95:%;95:10〉≤ππH HB. %95:%;95:10≠=ππH HC. %95:%;95:10〈≥ππH HD. %95:%;95:10≥〉ππH H6.对于非正态总体，使用统计量/x z s n =估计总体均值的条件是（ ）A ．小样本B ．总体方差已知C ．总体方差未知D ．大样本7.在假设检验中，原假设和备选假设（ ）A ．都有可能成立B ．都有可能不成立C ．只有一个成立而且必有一个成立D ．原假设一定成立，备选假设不一定成立8．一种零件的标准长度5cm ，要检验某天生产的零件是否符合标准要求，建立的原假设和备选假设就为（ ）A ．0:5H μ=，1:5H μ≠ B ．0:5H μ≠，1:5H μ>C ．0:5H μ≤，1:5H μ>D ．0:5H μ≥，1:5H μ< 9.若检验的假设为00:H μμ≥，10:H μμ<，则拒绝域为（ ） A ．z z α> B ．z z α<- C ．/2z z α<-或/2z z α<- D ．z z α>或z z α<-10.一家汽车生产企业在广告中宣称“该公司的汽车可以保证在2年或24000公里内无事故”，但该汽车的一个经销商认为保证“2年”这一项是不必要的，因为汽车车主在2年内行驶的平均里程不超过24000公里。

假设检验习题答案 Prepared on 22 November 20201．假设某产品的重量服从正态分布，现在从一批产品中随机抽取16件，测得平均重量为820克，标准差为60克，试以显着性水平=与=，分别检验这批产品的平均重量是否是800克。

解：假设检验为800:,800:0100≠=μμH H (产品重量应该使用双侧 检验)。

采用t 分布的检验统计量n x t /0σμ-=。

查出α＝和两个水平下的临界值(df=n-1=15)为和。

334.116/60800820=-=t 。

因为t <<，所以在两个水平下都接受原假设。

2．某牌号彩电规定无故障时间为10 000小时，厂家采取改进措施，现在从新批量彩电中抽取100台，测得平均无故障时间为10 150小时，标准差为500小时，能否据此判断该彩电无故障时间有显着增加(=解：假设检验为10000:,10000:0100>=μμH H （使用寿命有无显着增加，应该使用右侧检验）。

n=100可近似采用正态分布的检验统计量nx z /0σμ-=。

查出α＝水平下的反查正态概率表得到临界值到之间（因为表中给出的是双侧检验的接受域临界值，因此本题的单侧检验显着性水平应先乘以2，再查到对应的临界值）。

计算统计量值3100/5001000010150=-=z 。

因为z=3>(>，所以拒绝原假设，无故障时间有显着增加。

3.设某产品的指标服从正态分布，它的标准差σ已知为150，今抽了一个容量为26的样本，计算得平均值为1637。

问在5％的显着水平下，能否认为这批产品的指标的期望值μ为1600解: 01:1600, :1600,H H μμ=≠标准差σ已知,当0.05,α=26,n =96.1579.02/1==-z z α,由检验统计量1.25 1.96Z ===<,接受0:1600H μ=, 即,以95%的把握认为这批产品的指标的期望值μ为1600.4.某电器零件的平均电阻一直保持在Ω，改变加工工艺后，测得100个零件的平均电阻为Ω，如改变工艺前后电阻的标准差保持在Ω，问新工艺对此零件的电阻有无显着影响(α=解: 01: 2.64, : 2.64,H H μμ=≠已知标准差σ=, 当0.05,α=96.1579.02/1==-z z α100,n =由检验统计量 3.33 1.96Z ===>,接受1: 2.64H μ≠, 即, 以95%的把握认为新工艺对此零件的电阻有显着影响.5．某食品厂用自动装罐机装罐头食品，每罐标准重量为500克，每隔一定时间需要检查机器工作情况。

假设检验作业1. 一种罐装饮料采用自动生产线生产，每罐的容量是255ml （总体的均值 ），标准差为5ml （总体的标准差）。

为检验每罐容量是否符合要求，质检人员在某天生产的饮料中随机抽取了40罐进行检验，测得每罐平均容量为255.8ml （样本的均值）。

取显著性水平=0.05 ，检验该天生产的饮料容量是否符合标准要求？ 解：正态，总体方差已经，大样本，Z 检验统计量，双侧检验 96.105.040/52558.255)1,0(~n /2552552010==-=-=≠=αασμμμZ N X Z H H ：： 若计算的Z 值在（-1.96，1.96）之间，不能拒绝原假设，认为符合标准；反之，拒绝原假设，即产品不符合标准。

2. 某一小麦品种的平均产量为5200kg/hm2 。

一家研究机构对小麦品种进行了改良以期提高产量。

为检验改良后的新品种产量是否有显著提高，随机抽取了36个地块进行试种，得到的样本平均产量为5275kg/hm2，标准差为120/hm2 。

试检验改良后的新品种产量是否有显著提高？ (a=0.05)解：不知是否正态总体，总体标准差未知，但因是大样本，可用Z 分布检验统计量，右侧检验（注意临界值或拒绝域的确定，用图形表示更清楚）645.105.036/12052005275)1,0(~n /52005200010==-=-=≤ααμμμZ N s X Z H H ：：计算出的Z 值，若Z 值大于1.645则拒绝原假设；反之，不能拒绝原假设。

3. 一种以休闲和娱乐为主题的杂志，声称其读者群中有80%为女性。

为验证这一说法是否属实，某研究部门抽取了由200人组成的一个随机样本，发现有146个女性经常阅读该杂志。

分别取显著性水平 a=0.05和a=0.01 ，检验该杂志读者群中女性的比率是否为80%？注意：（1)有些书，用大写的π表示总体比例。

（2) 不同的显著性水平，可能得出不同的结论。

第8章 假设检验一、填空题1、 对正态总体的数学期望μ进行假设检验，如果在显著性水平0.05下，接受假设00:μμ=H ，那么在显著性水平0.01下，必然接受0H 。

2、在对总体参数的假设检验中，若给定显著性水平为α，则犯第一类错误的概率是α。

3、设总体),(N ~X 2σμ，样本n 21X ,X ,X Λ，2σ未知，则00:H μ=μ，01:H μ<μ的拒绝域为 )}1(/{0--<-n t nS X αμ，其中显著性水平为α。

4、设n 21X ,X ,X Λ是来自正态总体),(N 2σμ的简单随机样本，其中2,σμ未知，记∑==n 1i i X n 1X ，则假设0:H 0=μ的t 检验使用统计量=T Q n n X )1(- .二、计算题1、某食品厂用自动装罐机装罐头食品，规定标准重量为250克，标准差不超过3克时机器工作 为正常，每天定时检验机器情况，现抽取16罐，测得平均重量252=X 克，样本标准差4=S 克，假定罐头重量服从正态分布，试问该机器工作是否正常？解：设重量),(~2σμN X 05.016==αn 4252==S X(1)检验假设250:0=μH 250:1≠μH ，因为2σ未知，在0H 成立下，)15(~/250t n S X T -=拒绝域为)}15(|{|025.0t T >，查表得1315.2)5(025.0=≠t由样本值算得1315.22<=T ，故接受0H(2)检验假设9:20=σH 9:201>σH 因为μ未知，选统计量2022)1(σS n x -= 在0H 成立条件下，2x 服从)15(2x 分布，拒绝域为)}15({205.02x x >，查表得996.24)15(205.0=x ， 现算得966.24667.26916152>=⨯=x ？拒绝0H ， 综合(1)和(2)得，以为机器工作不正常2、一种电子元件，要求其使用寿命不得低于1000小时，现在从一批这种元件中随机抽取25 件，测得其寿命平均值为950小时，已知该种元件寿命服从标准差100=σ小时正态分布， 试在显著性水平0.05下确定这批产品是否合格.解：设元件寿命),(~2σμN X ，2σ已知10002=σ，05.0,950,25===αX n检验假设1000:0=μH 1000:1<μH在2σ已知条件下，设统计量)1,0(~/1000N n X σμ-=拒绝域为}{05.0μμ<，查表得645.195.005.0-=-=μμ 而645.15.2205025/1001000950-<-=-=-=μ 拒绝假设0H 选择备择假设1H ，所以以为这批产品不合格.3. 对 显 著 水 平 a ， 检 验假 设 H 0 ; m = m 0， H 1 ; m ≠ m 0， 问当 m 0， m ， a一 定 时 ，增大样本量 n 必 能 使 犯 第 二 类 错 误 概 率 b 减 少 对 吗 ？并 说 明 理由 。

第9章 关联性分析 思考与练习参考答案一、最佳选择题1. 对简单相关系数作假设检验，)(v t t ，统计结论为（ B ）。

A. 两变量不相关B. 两变量有线性关系C. 两变量无线性关系D. 两变量不会是曲线关系，一定是线性关系E. 上述说法都不准确2. 计算积矩相关系数要求（ C ）。

A. Y 是正态变量，X 可以不满足正态的要求B. X 是正态变量，Y 可以不满足正态的要求C. 两变量都要求满足正态分布规律D. 两变量只要是测量指标就行E. Y 是定量指标，X 可以是任何类型的数据3. 对两个分类变量的频数表资料作关联性分析，可用（ C ）。

A. 积矩相关B.秩相关C. 关联系数D. 线性相关E.以上均可4. 由样本算得相关系数r ，t 检验结果为P <0.01，说明（ D ）。

A. 两变量之间有高度相关性B. r 来自高度相关的总体C. r 来自总体相关系数为0的总体D. r 来自总体相关系数不为0的总体E. r 来自总体相关系数大于0的总体二、思考题1. 1988年某地抽查0~7岁儿童营养不良患病情况如教材表9-10，某医师要想了解年龄与营养不良患病率是否有关，你认为应选用什么统计方法？为什么？教材表9-10 1988年某地抽查0～7岁儿童营养不良患病情况 年龄/岁 0~ 1~ 2~ 3~ 4~ 5~ 6~7 患病人数 98 278 86 29 59 82 34 患病率/%15.711.712.97.48.97.35.1解：提示,用秩相关分析年龄与患病率的关系，因患病率资料一般不服从正态分布。

2. 请查找最近三年主题为相关分析或关联分析的已发表国内医学文献，至少认真阅读其中3篇（建议分别选取Pearson 、Spearman 相关分析和关联分析各1篇），找出其中不妥之处。

3. 在讲散点图时，我们曾提到分层应慎重，有可能出现分层分析与总体情况大相径庭的结果。

请举一两个实例说明这种现象。

假设检验习题答案
单击此处添加副标题
汇报人姓名 汇报日期
目 录CATALOGUE
1 假设检验的基本概念 2 参数假设检验 3 非参数假设检验 4 习题答案与解析
ONE
1
假设检验的基本概念
定义与目的
判断该假设是否成 立，从而做出接受 或拒绝该假设的决 策。
假设检验是一种统计方法，用于根据样本数据对 某一假设进行评估。
假设检验的类型
单侧检验 只关注某一方向的假设是否成立。
参数检验 对总体参数进行假设检验。
双侧检验 同时关注两个方向的假设是否成立。
非参数检验 不涉及总体参数的假设检验。
ONE
2
参数假ቤተ መጻሕፍቲ ባይዱ检验
单参数假设检验
在单参数假设检验 中，我们通常会对 一个总体参数提出 假设，然后使用样 本数据来检验这个 假设。例如，我们 可能会假设一组数 据的平均值等于某 个值，然后使用样 本数据来检验这个 假设是否成立。
据是否符合正态分布、泊松分布等。
ONE
4
习题答案与解析
习题一答案与解析
答案：D
logo
解析：根据题目给出的数据，我们首先计 算出平均值和标准差。然后，利用假设检 验的方法，我们计算出Z统计量并确定其所 属的临界区间。根据临界区间的结果，我 们判断原假设是否被拒绝，并选择相应的 答案。
习题一答案与解析
秩次检验
详细描述
秩次检验将数据按照大小排序，并赋予每个数据 一个秩次值。然后比较两组数据的秩次分布是否 相同，以判断它们的相对大小关系。如果两组数 据的秩次分布相似，则可以认为它们的相对大小 关系相同；如果秩次分布不同，则可以认为它们 的相对大小关系不同。
秩次检验是一种非参数统计方法，用于比较两组 数据的相对大小关系。

8.1简述决策树分类的主要步骤答：决策树( Decision Tree )又称为判定树，是运用于分类的一种树结构。

其中的每个内部结点( internal node )代表对某个属性的一次测试，每条边代表一个测试结果，叶结点( leaf )代表某个类( class )或者类的分布( class distribution )，最上面的结点是根结点。

决策树分为分类树和回归树两种，分类树对离散变量做决策树，回归树对连续变量做决策树。

构造决策树是采用自上而下的递归构造方法。

决策树构造的结果是一棵二叉或多叉树，它的输入是一组带有类别标记的训练数据。

二叉树的内部结点(非叶结点)一般表示为一个逻辑判断，如形式为(a = b) 的逻辑判断，其中a 是属性，b 是该属性的某个属性值;树的边是逻辑判断的分支结果。

多叉树( ID3 )的内部结点是属性，边是该属性的所有取值，有几个属性值，就有几条边。

树的叶结点都是类别标记。

使用决策树进行分类分为两步：第1 步：利用训练集建立并精化一棵决策树，建立决策树模型。

这个过程实际上是一个从数据中获取知识，进行机器学习的过程。

第 2 步：利用生成完毕的决策树对输入数据进行分类。

对输入的记录，从根结点依次测试记录的属性值，直到到达某个叶结点，从而找到该记录所在的类8.6为什么朴素叶贝斯分类称为“朴素”的？简述朴素叶贝斯分类的主要思想。

答：朴素贝叶斯分类器是一种应用基于独立假设的贝叶斯定理的简单概率分类器。

之所以成为朴素，应该是Naive的直译，意思为简单，朴素，天真。

朴素贝叶斯分类是最常用的两大分类算法（决策树分类和朴素贝叶斯分类）。

分类是将一个未知样本分到几个预先已知类的过程。

朴素贝叶斯分类是基于贝叶斯概率的思想，假设属性之间相互独立，例如A和B，则P （B|A）代表A发生的情况下，B发生的概率。

8.7（b）答：决策树为：(salary = 26K...30K:junior= 31K...35K:junior= 36K...40K:senior= 41K...45K:junior= 46K...50K (department = secretary:junior= sales:senior= systems:Junior= marketing:senior)= 66K...70K:senior)（b）答：（c）答：设元组的各属性之间不独立，其联合概率不能写成份量相乘的形式。

假设检验习题及答案填空题1.原假设与备择假设是一个__________，也就是说在假设检验中原假设与备择假设只有一个成立，且必有一个成立。

（完备事件组）2.我们在检验某项研究成功与否时，一般以研究目标作为__________，如在研究新管理方法是否对销售业绩（周销售量）产生影响时，设原周销售量为A 元，欲对新管理方法效果进行检验，备择假设为__________。

（备择假设H1：μ>A）单选题从统计量出发，对总体某些特性的“假设”作出拒绝或接受的判断的过程称为( )A.参数估计B.统计推断C.区间估计D.假设检验答案：d2.假设检验的概率依据是( )。

A.小概率原理B.最大似然原理C.大数定理D.中心极限定理答案：a多选题1.统计推断包括以下几个方面的内容( )。

A.通过构造统计量，运用样本信息，实施对总体参数的估计B.从统计量出发，对总体某些特性的“假设”作出拒绝或接受的判断C.相关分析D.时间序列分析E.回归分析答案：a, b2.假设检验的基本思想是( )。

A.先对总体的参数或分布函数的表达式做出某种假设，然后找出一个在假设成立条件下出现可能性甚小的(条件)小概率事件。

B.如果试验或抽样的结果使该小概率事件出现了，这与小概率原理相违背，表明原来的假设有问题，应予以否定，即拒绝这个假设。

C.若该小概率事件在一次试验或抽样中并未出现，就没有理由否定这个假设，表明试验或抽样结果支持这个假设，这时称假设也实验结果是相容的，或者说可以接受原来的假设。

D.如果试验或抽样的结果使该小概率事件出现了，则不能否认这个假设。

E.若该小概率事件在一次试验或抽样中并未出现，则否定这个假设。

答案：a, b, c3.假设检验的具体步骤包括( )。

A.根据实际问题的要求，提出原假设及备择假设;B.确定检验统计量，并找出在假设成立条件下，该统计量所服从的概率分布;C.根据所要求的显着性水平和所选取的统计量，查概率分布临界值表，确定临界值与否定域;D.将样本观察值代入所构造的检验统计量中，计算出该统计量的值。