《统计学》-第12章-习题答案

12 - 8
统计学 四、国民经济核算的基本原则
STATISTICS
(一)计量社会产品的生产性原则和社会性原则 “生产性原则”是指国民经济核算应对生产活动的 全部有效成果进行计量。 “社会性原则”是指作为核算对象的生产成果还必 须具有社会性，即不仅是生产者个人所需要的，而 且还是社会所需要的，是能得到社会承认的成果。 (二)国民经济核算的平衡原则 社会产品的生产、分配和使用三者在总量上应该是 恒等或平衡的。这就是所谓的“平衡原则”，国外 有的学者将这种关系称作“三方等价原理”。
最常用的国民经济总量指标。
12 - 18
图12-2 常用国民经济统计指标
统计学
STATISTICS
二、国民经济生产指标
(一)国内总产出 “国内总产出”是指一定时期内国民经济各部门生产的社会 总产品的价值总量。 从实物形态看，社会总产品可分为货物和服务两大类。从价 值形态看，国内总产出是社会总产品完全价值的总和，其价 值构成为：(1)生产资料转移价值c，包括劳动手段转移价值 (固定资产折旧)c1和劳动对象转移价值(即中间消耗)c2 ；(2) 活劳动新创价值，包括必要劳动价值v和剩余劳动价值m 。 国内总产出包括了生产资料转移价值的大量重复计算，并且， 这种重复计算的程度还与生产组织的内部结构的变化有关。 国内总产出只是一个有关国民经济生产的“总周转量”指标， 它能够表明全社会生产活动的总规模，并能用于对国民经济 各部门间的技术经济联系进行投入产出分析，但不能说明国 民经济生产活动的最终成果。
12 - 12
统计学 三、国民经济核算的行业与部门分类
STATISTICS
（一）机构部门分类和活动部门分类 1. 机构部门分类。按其在取得收入和支配收入、筹集资金和 运用资金的财务决策权同一性标准进行分类的一种方法。分 类的基本单位是能够拥有资产、承担负债，从事经济活动并 与其它单位进行经济交易的实体。 我国新国民经济核算体系中，常住单位分为四个机构部门： （1）非金融企业部门。 （2）金融机构部门。 （3）政府部门。 （4）住户部门。 2.活动部门分类。按各基层单位活动性质的同类性对掌握生 产经营决策权的基层单位进行分类。这种分类存在层次差别， 根据分析的需要，可粗可细。

dfR 1
MSR
SSR dfR
=118.95
dfE N 2 =8
MSE
SSE dfE
8.08
F MSR =14.72 MSE
查 F 表， F0.01(1,8) 5.32 ， F F0.05(1,8)
5．某研究所 10 名学生研习某教授的高级统计课程，期中与期末考试成绩见下表。请 问该教授是否可以利用期中考试成绩来预测期末考试成绩?
4/6
圣才电子书 十万种考研考证电子书、题库视频学习平台

解：（1）建立回归方程
经计算 X 79.2， Y 84.2， sX 8.75， sY =4.52
dfE N 2 =8
MSE
SSE dfE
230.5
F MSR =9.15 MSE
查 F 表， F0.05(1,8) 5.32 ， F F0.05(1,8)
3/6
圣才电子书

方差分析表如下
十万种考研考证电子书、题库视频学习平台
变异来源
自由度
平方和
均方
F
F0.05(1,8)
bYX
Y Y
2
=0.57
X X
a Y bX 23.13
则回归方程为 Yˆ 23.13 0.57X 。
（2）对回归方程进行检验
SST
Y2
Y 2
N
=3952.5
SSR
b2
X
2
X
N
2
=2108.6
SSE SST SSR =1843.9
dfR 1
MSR
SSR dfR
=2108.6
SST SSR N 2
MSE =15.18
2

贾俊平《统计学》课后习题答案在线阅读：https:///cUb7v8DC
【解析】数据的测量尺度有四种：①分类尺度，即名义尺度。按照事物的某种属性对其进行 平行的分类，数据表现为类别，如“性别”。②顺序尺度。对事物类别顺序的测度，数据表 现为有序的类别，如“产品登记”“受教育程度”。③差距尺度。对事物类别或次序之间间 距的测度，没有绝对零点，数据表现为数字。④比例尺度。对事物类别或次序之间间距的测 度，有绝对零点，数据表现为数字。 8 以下关于参数和统计量的说法正确的是（ ）。[中央财经大学 2011 研] A．总体参数是随机变量 B．样本统计量都是总体参数的无偏估计量 C．对一个总体参数进行估计时，统计量的表达式是唯一的 D．样本统计量是随机变量 【答案】D 【解析】参数是用来描述总体特征的概括性数字度量，研究者所关心的参数通常有总体平均 数、总体标准差、总体比例等，由于总体数据通常是不知道的，所以参数是一个未知的常数。 无偏性是指估计量抽样分布的数学期望等于被估计的总体参数，并非所有的估计量都具有无 偏性。对总体参数进行估计时，用不同估计方法得到的估计量可能不同。统计量是根据样本 数据计算出来的一个量，由于抽样是随机的，因此统计量是样本的函数，是随机变量。 9 以下哪一种情形涉及定性数据的收集？（ ）[中山大学 2012 研] A．质量控制工程师测量电灯泡的寿命 B．社会学家通过抽样调查来估计广州市市民的平均年收入 C．运动器材厂家在区分各大俱乐部棒球选手是左撇子还是右撇子时做的调查 D．婚礼策划公司通过抽样调查来估计上海市市民举办婚礼的平均开销 【答案】C
试读（部分内容）
第 1 章 导 论 一、单项选择题 1 在抽样推断中，总体参数是一个（ ）。[中央财经大学 2018 研]
贾俊平《统计学》课后习．已知的量 C．统计量 D．确定的量 【答案】D 【解析】参数是用来描述总体特征的概括性数字度量，它是研究者想要了解的总体的某种特 征值。由于总体数据通常是不知道的，所以参数是一个未知的确定的常数。 2 统计年鉴中 2016 年全国各大城市的人均家庭收入数据属于（ ）。[中央财经大学 2018 研] A．定类数据 B．定序数据 C．截面数据 D．时间序列数据 【答案】C 【解析】按照被描述的现象与时间的关系，可以将统计数据分为截面数据和时间序列数据。 截面数据是在相同或近似相同的时间点上收集的数据，这类数据通常是在不同的空间获得 的，用于描述现象在某一时刻的变化情况。比如，2010 年我国各地区的国内生产总值就是 截面数据。时间序列数据是在不同时间收集到的数据，这类数据是按时间顺序收集到的，用 于描述现象随时间变化的情况。比如 2010～2012 年我国的国内生产总值就是时间序列数 据。 3 在教学评估中，某省三所高校的等级分别是优秀、良好、及格，则“等级”是（ ）。 [浙江工商大学 2017 研]

径
x=read.table(“li12.1.txt”,header=T) #从li11.1.txt中读 入数据，记为x。
(或者：x<c(500,505,482,480,481,501,498,482, 490,481) #输入样本数据x)
t.test(x,mu=500) #检验总体均值是否等于500
Z pˆ p0
p0 1 p0
质量 500 505 482 480 481 501 490 498
频数 20 16 9 1 8 20 8 18
以0.05为显著水平检验：包装机包装出来的茶叶 的平均质量是否为标准质量500克？
2012-6-26
【统计理论】
当样本来自于非正态总体时，要检验总体 均值是否等于某个常数，在原假设成立且n 充分大时，近似地有：
*
《统计学实验》第12章假设检验
(2) 这是一个左侧检验问题，即 H0 : 500 H1 : 500
处理方法与（1）类似，具体程序如下：
x<-c(500,505,482,480,481,501,498,482, 490,481) #输入样本数据x
t.test(x,mu=500,alternative="less") #备择
t = -3.4912, df = 16, p-value = 0.9985
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
-343.1434 Inf
sample estimates:
平均使用寿命短？
2012-6-26

统计学课后习题及答案统计学课后习题及答案统计学是一门研究数据收集、分析和解释的学科，它在各个领域都有广泛的应用。

作为学习统计学的学生，课后习题是巩固知识、提高技能的重要途径。

本文将提供一些统计学课后习题及其答案，希望对学习者有所帮助。

1. 描述性统计习题：给定以下一组数据：10, 15, 12, 18, 20, 22, 16, 10, 14, 19。

请计算该组数据的均值、中位数和众数，并解释它们的含义。

答案：均值：计算方法是将所有数据相加，然后除以数据的个数。

对于给定的数据，均值为（10+15+12+18+20+22+16+10+14+19）/10 = 16.6。

中位数：将数据按照从小到大的顺序排列，找出中间的数。

对于给定的数据，中位数为16。

众数：出现频率最高的数。

对于给定的数据，众数为10。

这些统计量可以帮助我们了解数据的集中趋势。

均值是所有数据的平均值，中位数是数据的中间值，众数是出现频率最高的值。

在这个例子中，均值告诉我们这组数据的平均水平是16.6，中位数告诉我们大约一半的数据小于16，一半的数据大于16，众数告诉我们10是这组数据中出现次数最多的数。

2. 概率习题：一个骰子有6个面，每个面上的数字分别是1、2、3、4、5、6。

如果投掷一次骰子，求得到奇数的概率。

答案：奇数的个数为3个，即1、3、5。

骰子的总个数为6个。

所以得到奇数的概率为3/6 = 1/2。

概率是事件发生的可能性。

在这个例子中，奇数的个数是3个，总个数是6个，所以得到奇数的概率是3/6，即1/2。

3. 抽样与估计习题：某市有1000名居民，你希望了解他们对某项政策的态度。

你打算进行一次调查，抽取100名居民进行问卷调查。

这个调查结果能否代表整个市民的态度？为什么？答案：这个调查结果不能代表整个市民的态度。

原因是抽样的方式可能引入抽样误差。

如果抽取的100名居民在某些特征上不具有代表性，比如年龄、性别、职业等，那么调查结果可能会偏离整个市民的态度。

d t /2(N P 1) SE / (N P 1) = t0.05(7)×0.8618 = 1.63
∴该商品在该市下一年的年需求量的置信度为90% 的预测区间为
( yˆ0 d, yˆ0 d ) = (11.20万台，14.46万台)
15
2. 控制
在多元回归情况下，由于解释变量有多个，若控制
当模型中解释变量很多时，通常会存在较多的不显 著变量，以上步骤就非常繁琐。更为有效的方法是采 用“逐步回归”来求解多元线性回归方程。
9
逐步回归方法简介
逐步回归的基本思想是： 采用一定的评价标准，将解释变量一个一个地逐步 引入回归方程。每引进一个新变量后，都对方程 中的所有变量进行显著性检验，并剔除不显著的 变量，被剔除的变量以后就不再进入回归方程。 采用逐步回归方法最终所得到的回归方程与前述方 法的结果是一样的，但计算量要少得多。 在 SPSS 软件的线性回归功能中就提供了逐步回归 的可选项。
16
案例3的控制要求分析
假定下一年度居民家庭的年平均收入估计在 30000-31000元之间，若要以90％概率使该商品在 的年需求量不低于12万台，问应将价格控制在什 么范围内？。 解：此问题仍是单测控制问题，即要控制 X1 的取值
范围，使 P{yˆ d 12} 0.90
其中 d t (N P 1) SE /(N P 1) = t0.1(7)×0.8618 = 1.2194
d t /2(N P 1) SE / (N P 1)
14
案例3的预测分析
预计下一年度该商品的价格水平为1800元，家庭 年平均收入为30000元，求该商品年需求量的置信 度为90%的预测区间。 解：由所得回归方程，可求得
yˆ0 11.167 1.903 1.8 0.1695 30 12.83

第1章统计和统计数据第2章 1.1 指出下面的变量类型。

第3章（1）年龄。

第4章（2）性别。

第5章（3）汽车产量。

第6章（4）员工对企业某项改革措施的态度（赞成、中立、反对）。

第7章（5）购买商品时的支付方式（现金、信用卡、支票）。

第8章详细答案：第9章（1）数值变量。

第10章（2）分类变量。

第11章（3）数值变量。

第12章（4）顺序变量。

第13章（5）分类变量。

第14章1.2 一家研究机构从IT从业者中随机抽取1000人作为样本进行调查，其中60%回答他们的月收入在5000元以上，50%的人回答他第15章们的消费支付方式是用信用卡。

第16章（1）这一研究的总体是什么？样本是什么？样本量是多少？第17章（2）“月收入”是分类变量、顺序变量还是数值变量？第18章（3）“消费支付方式”是分类变量、顺序变量还是数值变量？第19章详细答案：第20章（1）总体是“所有IT从业者”，样本是“所抽取的1000名IT从业者”，样本量是1000。

第21章（2）数值变量。

第22章（3）分类变量。

第23章1.3 一项调查表明，消费者每月在网上购物的平均花费是200元，他们选择在网上购物的主要原因是“价格便宜”。

第24章（1）这一研究的总体是什么？第25章（2）“消费者在网上购物的原因”是分类变量、顺序变量还是数值变量？第26章详细答案：第27章（1）总体是“所有的网上购物者”。

第28章（2）分类变量。

第29章1.4 某大学的商学院为了解毕业生的就业倾向，分别在会计专业抽取50人、市场营销专业抽取30、企业管理20人进行调查。

第30章（1）这种抽样方式是分层抽样、系统抽样还是整群抽样？第31章（2）样本量是多少？第32章详细答案：第33章（1）分层抽样。

第34章（2）100。

第2章用图表展示数据（3）帕累托图如下：（4）饼图如下：2.2 为确定灯泡的使用寿命（单位：小时），在一批灯泡中随机抽取100只进行测试，所得数据如下：710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100（2）直方图如下：从直方图可以看出，灯泡使用寿命的分布基本上是对称的。

4.用Excel汇总第二季度中三个月份的资料，用（）功能。（知识点3.3答案：B）
A．透视表B.合并计算C.单变量求解D.分类汇总
5.小张收集了1957-2007年中国GDP的数据，如果要反映这50年我国生产发展的趋势，用什么图形最为合适？（）（知识点3.5答案：D）
A.直方图B.散点图C.饼图D.折线图
37
பைடு நூலகம்33.6
130-140
12
10.9
103
93.6
19
17.3
140-150
5
4.5
108
98.2
7
6.4
150-160
2
1.8
110
100.0
2
1.8
合计
110
100
—
—
—
—
A.树苗高度低于110厘米的占总数的39.1%B.树苗高度低于110厘米的占总数的84.5%
C.树苗高度高于130厘米的有19棵D.树苗高度高于130厘米的有103棵
第二章数据的收集与整理
2.1数据的来源
2.2统计调查方案设计
2.3调查方法
2.4调查的组织方式：普查、抽样调查、重点调查、典型调查
2.5抽样的组织方式：简单随机抽样、系统抽样、分层抽样、整群抽样
2.6数据的审定：误差
2.7数据的分组
2.8.编制次数分布表：频数（次数）、频率
习题
一、单项选择题
1．小吴为写毕业论文去收集数据资料，（）是次级数据。(知识点：2.1答案：C)
A.指标B.标志C.变量D.标志值
8.以一、二、三等品来衡量产品质地的优劣，那么该产品等级是（）。(知识点：1.7答案：A)
A.品质标志B.数量标志C.质量指标D.数量指标

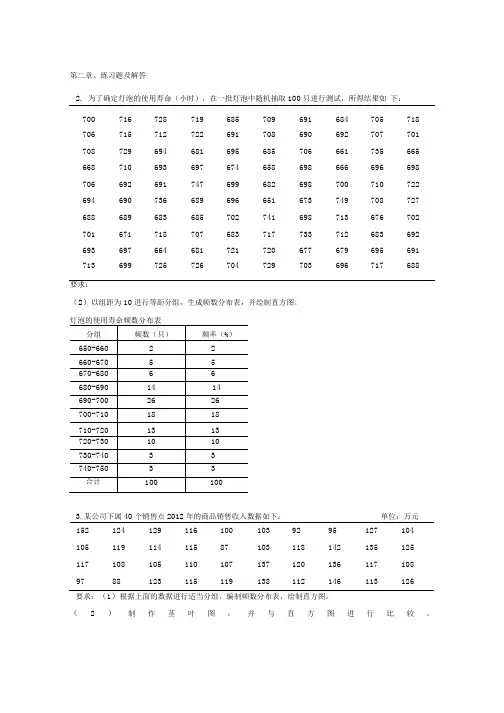
第二章、练习题及解答2.为了确定灯泡的使用寿命（小时），在一批灯泡中随机抽取100只进行测试，所得结果如下：700 716 728 719 685 709 691 684 705 718 706 715 712 722 691 708 690 692 707 701 708 729 694 681 695 685 706 661 735 665 668 710 693 697 674 658 698 666 696 698 706 692 691 747 699 682 698 700 710 722 694 690 736 689 696 651 673 749 708 727 688 689 683 685 702 741 698 713 676 702 701 671 718 707 683 717 733 712 683 692 693 697 664 681 721 720 677 679 695 691 713 699 725 726 704 729 703 696 717 688要求：（2）以组距为10进行等距分组，生成频数分布表，并绘制直方图。

3.某公司下属40个销售点2012年的商品销售收入数据如下：单位：万元152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 10897 88 123 115 119 138 112 146 113 126要求：（1）根据上面的数据进行适当分组，编制频数分布表，绘制直方图。

（2）制作茎叶图，并与直方图进行比较。

1.已知下表资料:25 20 10 500 2.5 30 50 25 1500 7.5 35 80 40 2800 14 40 36 18 1440 7.2 4514 7 630 3. 15 合 计200100687034. 35_y xf 6870根据频数计算工人平均日产量：〒=金^ =北* = 34.35 （件）£f 200结论：对同一资料，采用频数和频率资料计算的变量值的平均数是一致的。

第11章一元线性回归一、思考题1．解释相关关系的含义，说明相关关系的特点。

答：变量之间存在的不确定的数量关系，称为相关关系。

相关关系的特点：一个变量的取值不能由另一个变量唯一确定，当变量x取某个值时，变量y的取值可能有几个。

对这种关系不确定的变量是不能用函数关系进行描述的。

2．相关分析主要解决哪些问题？答：相关分析就是对两个变量之间线性关系的描述与度量，它要解决的问题包括：（1）变量之间是否存在关系；（2）如果存在关系，它们之间是什么样的关系；（3）变量之间的关系强度如何；（4）样本所反映的变量之间的关系能否代表总体变量之间的关系。

3．相关分析中有哪些基本假定？答：在进行相关分析时，对总体主要有以下两个假定：（1）两个变量之间是线性关系；（2）两个变量都是随机变量。

4．简述相关系数的性质。

答：相关系数是根据样本数据计算的度量两个变量之间线性关系强度的统计量。

若相关系数是根据总体全部数据计算的，称为总体相关系数，记为ρ；若是根据样本数据计算的，则称为样本相关系数，记为r 。

相关系数的性质：（1）r 的取值范围在－1～＋1之间，即－1≤r ≤1。

若0<r ≤1，表明x 与y 之间存在正线性相关关系；若－1≤r <0，表明x 与y 之间存在负线性相关关系；若r =＋1，表明x 与y 之间为完全正线性相关关系；若r =－1，表明x 与y 之间为完全负线性相关关系。

可见当|r |=1时，y 的取值完全依赖于x ，二者之间即为函数关系；当r ＝0时，说明y 的取值与x 无关，即二者之间不存在线性相关关系。

（2）r 具有对称性。

x 与y 之间的相关系数xy r 和y 与x 之间的相关系数yx r 相等，即xy r =yx r 。

（3）r 数值大小与x 和y 的原点及尺度无关。

改变x 和y 的数据原点及计量尺度，并不改变r 数值大小。

（4）r 仅仅是x 与y 之间线性关系的一个度量，它不能用于描述非线性关系。

第1章统计与统计数据一、学习指导统计学是处理和分析数据的方法和技术，它几乎被应用到所有的学科检验领域。

本章首先介绍统计学的含义和应用领域，然后介绍统计数据的类型及其来源，最后介绍统计中常用的一些基本概念。

本章各节的主要内容和学习要点如下表所示。

二、主要术语1. 统计学：收集、处理、分析、解释数据并从数据中得出结论的科学。

2. 描述统计：研究数据收集、处理和描述的统计学分支。

3. 推断统计：研究如何利用样本数据来推断总体特征的统计学分支。

4. 分类数据：只能归于某一类别的非数字型数据。

5. 顺序数据：只能归于某一有序类别的非数字型数据。

6. 数值型数据：按数字尺度测量的观察值。

7. 观测数据：通过调查或观测而收集到的数据。

8. 实验数据：在实验中控制实验对象而收集到的数据。

9. 截面数据：在相同或近似相同的时间点上收集的数据。

10. 时间序列数据：在不同时间上收集到的数据。

11. 抽样调查：从总体中随机抽取一部分单位作为样本进行调查，并根据样本调查结果来推断总体特征的数据收集方法。

12. 普查：为特定目的而专门组织的全面调查。

13. 总体：包含所研究的全部个体（数据）的集合。

14. 样本：从总体中抽取的一部分元素的集合。

15. 样本容量：也称样本量，是构成样本的元素数目。

16. 参数：用来描述总体特征的概括性数字度量。

17. 统计量：用来描述样本特征的概括性数字度量。

18. 变量：说明现象某种特征的概念。

19. 分类变量：说明事物类别的一个名称。

20. 顺序变量：说明事物有序类别的一个名称。

21. 数值型变量：说明事物数字特征的一个名称。

22. 离散型变量：只能取可数值的变量。

23. 连续型变量：可以在一个或多个区间中取任何值的变量。

第2章数据的图表展示一、学习指导数据的图表展示是应用统计的基本技能。

本章首先介绍数据的预处理方法，然后介绍不同类型数据的整理与图示方法，最后介绍图表的合理使用问题。

本章各节的主要内容和学习二、主要术语24. 频数：落在某一特定类别（或组）中的数据个数。

1．设立假设。原假设为 备择假设为
2．给定显著性水平。取显著性水平 ，由于是双侧检验，因此需要确定上下两个临界值 和 。查表得到 ，所以。拒绝区间为小于-1.96或者大于1.96。
3．检验统计量
4．检验判断。
由于z的实际值在-1.96和1.96之间，没有落入拒绝区间，所以接受原假设，认为净重是符合规定
（五）计算题
1．因为2000年计划完成相对数是110%，所以
实际产值=
2000年计划产值比1999年增长8%，
所以1999年的计划产值=
那么2000年实际产值比1999年计划产值增长=
2．（1）
从第四年第四季度到第五年第三季度这一年的时间，实际上这一年的产量达到
则
这一题规定年末产量应达到170，所以提前时间按照水平法来算。
3．．根据题意，样本的平均数和标准差为
根据样本信息，计算统计量
4．检验判断。因为 ，所以在显著性水平0.01下，拒绝原假设，也就是说，含量是超过规定界限
第九章相关与回归
（一）判断题
1．×2．√3．√4．√5．×6．×7．×8．×
（二）单项选择题
1．① 2．① 3．③ 4．④ 5．④6．②7．②8．④
2．由题意
=8.89
3．由题意
令这个数为a。则
4．由题意
5．
销售额
售货员人数
组中值
20000-30000
30000-40000
40000-50000
50000-60000
60000-70000
70000-80000
80000以上
8
20
40
100
82
10
5
25000
35000

思考题与练习题参考答案【友情提示】请各位同学完成思考题和练习题后再对照参考答案。

回答正确，值得肯定；回答错误，请找出原因更正，这样使用参考答案，能力会越来越高，智慧会越来越多。

学而不思则罔，如果直接抄答案，对学习无益，危害甚大。

想抄答案者，请三思而后行！第一章绪论思考题参考答案1.不能，英军所有战机=英军被击毁的战机+英军返航的战机+英军没有弹孔的战机，因为英军被击毁的战机有的掉入海里、敌军占领区，或因堕毁而无形等，不能找回；没有弹孔的战机也不可能自己拿来射击后进行弹孔位置的调查。

即便被击毁的战机找回或没有弹孔的战机自己拿来射击进行实验，也不能从多个弹孔中确认那个弹孔是危险的。

2.问题：飞机上什么区域应该加强钢板？瓦尔德解决问题的思想：在他的飞机模型上逐个不重不漏地标示返航军机受敌军创伤的弹孔位置，找出几乎布满弹孔的区域；发现：没有弹孔区域是军机的危险区域。

3.能，拯救和发展自己的参考路径为：①找出自己的优点，②明确自己大学阶段的最佳目标，③拟出一个发扬自己优点，实现自己大学阶段最佳目标的可行计划。

练习题参考答案一、填空题1.调查。

2.探索、调查、发现。

3.目的。

二、简答题1.瓦尔德；把剩下少数几个没有弹孔的区域加强钢板。

2.统计学解决实际问题的基本思路，即基本步骤是：①提出与统计有关的实际问题；② 建立有效的指标体系；③收集数据；④选用或创造有效的统计方法整理、显示所收集数据的特征；⑤根据所收集数据的特征、结合定性、定量的知识作出合理推断；⑥根据合理推断给出更好决策的建议。

不解决问题时，重复第②-⑥步。

3.在结合实质性学科的过程中，统计学是能发现客观世界规律，更好决策，改变世界和培养相应领域领袖的一门学科。

三、案例分析题1．总体：我班所有学生；单位：我班每个学生；样本：我班部分学生；品质标志：姓名；数量标志：每个学生课程的成绩；指标：全班学生课程的平均成绩；指标体系：上学期全班同学学习的科目；统计量：我班部分同学课程的平均成绩；定性数据：姓名；定量数据：课程成绩；离散型变量：学习课程数；连续性变量：学生的学习时间；确定性变量：全班学生课程的平均成绩；随机变量：我班部分同学课程的平均成绩，每个同学进入教室的时间；横截面数据：我班学生月门课程的出勤率；时间序列数据：我班学生课程分别在第一个月、第二个月、第三个月、第四个月的出勤率；面板数据：我班学生课程分别在第一个月、第二个月、第三个月、第四个月的出勤率；选用描述统计。

12 - 32
Excel 输出结果的分析
SPSS共线性诊断
• • 自变量间的相关系数矩阵，观察是否存在自变量的相关系数非 常高。一般，相关系数>0.9将会存在共线性问题；相关系数在 0.8以上可能有问题 容忍度（Tolerance）：容忍度即以每个自变量作为应变量对其 他自变量进行回归分析时得到的残差比例，大小用1减决定系 数来表示。该指标越小，说明该自变量被其余自变量预测的越 精确，共线性可能就越严重。陈希孺根据经验得出：如果某个 自变量的容忍度小于0.1，则可能存在共线性问题严重 方差膨胀因子（Variance inflation factor,VIF）：实际上是容忍 度的倒数，VIF越大，说明共线性问题可能越严重 特征根（Eigenvalue）：实际上是对自变量进行主成分分析， 如果相当多维度的特征根约等于0，则可能有较严重的共线性 条件指数（Condition Index）：当某些维度的该指标数值大于 30时，可能存在共线性 12 - 33
12 - 35
多重共线性
(例题分析 例题分析) 例题分析
1. tα/2(25-2)=2.0687，所有统计量 α/2(25-2)=2.0687 ，所有统计量t>t 所以均拒绝原假设， 说明这4个自变量两两之间 ， 所以均拒绝原假设 ， 说明这 个自变量两两之间 都有显著的相关关系 由表Excel输出的结果可知 ， 回归模型的线性关系 输出的结果可知， 由表 输出的结果可知 显著(Significance-F＝ 1.03539E-06<α=0.05)。 而 显著 ＝ α 。 回 归 系 数 检 验 时 却 有 3 个 没 有 通 过 t 检 验 (PValue=0.074935 、 0.862853 、 0.067030>α=0.05) α 。这也暗示了模型中存在多重共线性 固定资产投资额的回归系数为负号(-0.029193) ， 固定资产投资额的回归系数为负号 与预期的不一致

统计学课本课后作业题（全）题目：第1章：P11 6，7第2章：P52 练习题3、9、10、11第3章： P116思考题12、14 练习题16、25第4章：P114 思考题6，练习题2、4、6、13第5章：P179 思考题4、练习题3、4、6、11第6章： P209 思考题4、练习题1、3、6第7章： P246思考题1、练习题1、7第8章： P287 思考题4、10 练习题2、3第一章6．．一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。

因此，他们开始检查供货商的集装箱，有问题的将其退回。

最近的一个集装箱装的是2 440加仑的油漆罐。

这家零售商抽查了50罐油漆，每一罐的质量精确到4位小数。

装满的油漆罐应为4.536 kg。

要求：(1)描述总体；最近的一个集装箱内的全部油漆；(2)描述研究变量；装满的油漆罐的质量；(3)描述样本；最近的一个集装箱内的50罐油漆；(4)描述推断。

50罐油漆的质量应为×50＝226.8 kg。

7．“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。

这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨而颇具特色。

假定作为百事可乐营销战役的一部分，选择了1000名消费者进行匿名性质的品尝试验(即在品尝试验中，两个品牌不做外观标记)，请每一名被测试者说出A品牌或B品牌中哪个口味更好。

要求：答：(1)总体：市场上的“可口可乐”与“百事可乐”(2)研究变量：更好口味的品牌名称；(3)样本：1000名消费者品尝的两个品牌(4)推断：两个品牌中哪个口味更好。

第二章3.某百货公司连续40天的商品销售额如下（单位：万元）：41 25 29 47 38 34 30 38 43 4046 36 45 37 37 36 45 43 33 4435 28 46 34 30 37 44 26 38 4442 36 37 37 49 39 42 32 36 35根据上面的数据进行适当的分组，编制频数分布表，并绘制直方图。

3 / 97
圣才电子书 十万种考研考证电子书、题库视频学习平台
4 / 97
圣才电子书 十万种考研考证电子书、题库视频学习平台

图 11-1 不同形态的散点图
（4）相关系数
通过散点图可以判断两个变量之间有无相关关系，并对变量间的关系形态作出大致的描
有所差异。样本相关系数是总体相关系数的一致估计量。样本相关系数记为 r，其计算公式
为：
r
n xy x y
n x2 ( x)2 n y2 ( y)2
按照上述计算公式计算的相关系数也称为线性相关系数，或 Pearson 相关系数。 ②相关系数的性质 a．r 的取值范围在－1～＋1 之间，即－1≤r≤1。若 0＜r≤1，表明 x 与 y 之间存在正 线性相关关系；若－1≤r＜0，表明 x 与 y 之间存在负线性相关关系；若 r＝＋1，表明 x 与
5 / 97
圣才电子书 十万种考研考证电子书、题库视频学习平台

y 之间为完全正线性相关关系；若 r＝－1，表明 x 与 y 之间为完全负线性相关关系。可见当 |r|＝1 时，y 的取值完全依赖于 x，二者之间即为函数关系；当 r＝0 时，说明 y 的取值与 x 无关，即二者之间不存在线性相关关系。|r|→1 说明两个变量之间的线性关系越强；|r|→0 说明两个变量之间的线性关系越弱。
b．r 具有对称性。x 与 r 之间的相关系数 rxy 和 y 与 x 之间的相关系数 ryx 相等，即 rxy ＝ryx。
c．r 数值大小与 x 和 y 的原点及尺度无关。改变 x 和 y 的数据原点及计量尺度，并不 改变 r 的数值大小。
述，但不能准确反映变量之间的关系强度。需要计算相关系数来准确度量两个变量之间的关
系强度。

第十二章实验设计12.1一项关于在干旱地区生长的一种杨树（Populus euphratica），在土壤中的水分逐渐丧失后，其基因表达、蛋白谱、生态生理学及生长性能等方面产生可逆性改变的研究。

作者在本实验的5个时间点上（H5为对照），用qPCR方法度量了该杨树叶子中的三个基因的转录丰度比[83]，表中给出的为阵列数据：GenBank ID 基因H1H2H3H4H5AJ 780 423 半胱氨酸蛋白酶0.7 1.0 2.3 13.1 1.9AJ 780 698 环核苷酸和钙调节的离子通道 1.5 1.2 3.0 4.3 1.5AJ 777 362 核糖体蛋白 1.1 1.1 1.0 0.9 1.2借用上述数据，以三个基因作为三个区组，计算在5个时间点上转录丰度比差异是否显著？答：随机化完全区组实验设计方差分析的程序，类似于两因素交叉分组实验设计。

以下是本题的程序和结果：options linesize=76 nodate;data poplar;do block=1 to 3;do time=1 to 5;input trans @@;output;end;end;cards;0.7 1.0 2.3 13.1 1.91.5 1.2 3.0 4.3 1.51.1 1.1 1.0 0.9 1.2;proc anova;class block time;model trans=block time;run;The SAS SystemThe ANOVA ProcedureClass Level InformationClass Levels Valuesblock 3 1 2 3time 5 1 2 3 4 5Number of observations 15The SAS SystemThe ANOVA ProcedureDependent Variable: transSum ofSource DF Squares Mean Square F Value Pr > F Model 6 72.5560000 12.0926667 1.53 0.2809Error 8 63.1013333 7.8876667Corrected Total 14 135.6573333R-Square Coeff Var Root MSE trans Mean0.534848 117.6745 2.808499 2.386667Source DF Anova SS Mean Square F Value Pr > F block 2 18.82533333 9.41266667 1.19 0.3519 time 4 53.73066667 13.43266667 1.70 0.2416从上表中的结果可以看出，如果按随机化完全区组设计进行分析，不同时间点之间的差异不显著。