椭圆(高三复习课)

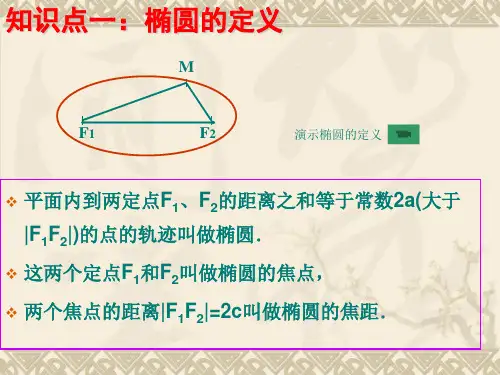
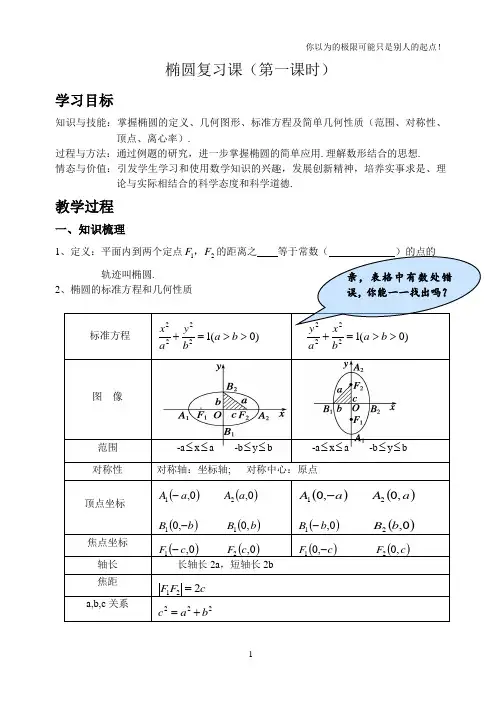
椭圆复习课（第一课时）学习目标知识与技能：掌握椭圆的定义、几何图形、标准方程及简单几何性质（范围、对称性、顶点、离心率）.过程与方法：通过例题的研究，进一步掌握椭圆的简单应用.理解数形结合的思想. 情态与价值：引发学生学习和使用数学知识的兴趣，发展创新精神，培养实事求是、理论与实际相结合的科学态度和科学道德.教学过程一、知识梳理1、定义：平面内到两个定点21F F ，的距离之 等于常数（ ）的点的 轨迹叫椭圆.2、椭圆的标准方程和几何性质标准方程22221(0)x y a b a b +=>> )0(12222>>=+b a b x a y 图 像范围 -a ≤x ≤a -b ≤y ≤b -a ≤x ≤a -b ≤y ≤b对称性 对称轴：坐标轴; 对称中心：原点顶点坐标()0,1a A - ()0,2a A ()b B -,01 ()b B ,01()a A -,01 ()a A ,02 ()0,1b B - ()0,2b B焦点坐标 ()0,1c F - ()0,2c F()c F -,01 ()c F ,02轴长 长轴长2a ，短轴长2b焦距 c F F 221=a,b,c 关系222b a c +=亲，表格中有数处错误，你能一一找出吗？离心率1>=ac e（1）动点P 到两定点A （–2，0）,B(2，0)的距离之和为4，则点P 的轨迹是椭圆.（ ）（2）若椭圆1ky 4x 22=+的焦距是22，则k=2. ( )三、能力提升考点一 椭圆的定义及其标准方程例1：已知椭圆以坐标轴为对称轴，求分别满足下列条件的椭圆的标准方程.（1）一个焦点为（2，0），离心率为 ；（2）过 ()23,N 1,6M ，），（-两点.直击高考已知椭圆C: 1b y a x 2222=+(a>b>0)的左右焦点为21F F ，，离心率为33，过2F 的直线L 交C 于A ，B 两点，若B AF 1∆的周长为43，则C 的方程为（ ）A.12y 3x 22=+B. 1y 3x 22=+ C. 18y 12x 22=+ D. 14y 12x 22=+变式提升：设21F F ，分别是椭圆116y 25x 22=+的左、右焦点，P 为椭圆上一点，M 是P F 1的中点，|OM| =3，则P 点到椭圆左焦点的距离为 （ ）A.4B.3C.2D.521=e X YPO xyBOA1F1F2F2FM考点二、椭圆的几何性质例2、已知椭圆C: 1b y a x 2222=+(a>b>0)的左右焦点为21F F ，，P 是椭圆短轴的一个端点，且21PF PF ⊥,则椭圆的离心率为 .变式提升椭圆C ：1by a x 2222=+（a ＞b ＞0）的左、右焦点分别为21F F ，，焦距为2c ，若直线y=3（x+c ）与椭圆C 的一个交点M 满足12212F MF F MF ∠=∠，则该椭圆的离心率等于 .互动探究已知椭圆C: 1by a x 2222=+(a>b>0)的左右焦点为21F F ，，M 为椭圆上一点，021=•M F M F ,则椭圆离心率的范围是 .XYMO1F2FYOXP1F2F探究思考1)本题中若P 点在椭圆内部，其他条件不变，试求之。