电磁场理论(柯亨玉)答案第三章静态电磁场.pdf
- 格式:pdf
- 大小:298.68 KB
- 文档页数:12



《电磁场与电磁波》知识点及参考答案第1章 矢量分析1、如果矢量场F 的散度处处为0,即0F∇⋅≡,则矢量场是无散场,由旋涡源所产生,通过任何闭合曲面S 的通量等于0。
2、如果矢量场F 的旋度处处为0,即0F ∇⨯≡,则矢量场是无旋场,由散度源所产生,沿任何闭合路径C 的环流等于0。
3、矢量分析中的两个重要定理分别是散度定理(高斯定理)和斯托克斯定理, 它们的表达式分别是:散度(高斯)定理:SVFdV F dS ∇⋅=⋅⎰⎰和斯托克斯定理:sCF dS F dl∇⨯⋅=⋅⎰⎰。
4、在有限空间V 中,矢量场的性质由其散度、旋度和V 边界上所满足的条件唯一的确定。
( √ )5、描绘物理状态空间分布的标量函数和矢量函数,在时间为一定值的情况下,它们是唯一的。
( √ )6、标量场的梯度运算和矢量场的旋度运算都是矢量。
( √ )7、梯度的方向是等值面的切线方向。
(× )8、标量场梯度的旋度恒等于0。
( √ ) 9、习题1.12, 1.16。
第2章 电磁场的基本规律(电场部分)1、静止电荷所产生的电场,称之为静电场;电场强度的方向与正电荷在电场中受力的方向相同。
2、在国际单位制中,电场强度的单位是V/m(伏特/米)。
3、静电系统在真空中的基本方程的积分形式是:V V sD d S d V Q ρ⋅==⎰⎰和0lE dl ⋅=⎰。
4、静电系统在真空中的基本方程的微分形式是:V D ρ∇⋅=和0E∇⨯=。
5、电荷之间的相互作用力是通过电场发生的,电流与电流之间的相互作用力是通过磁场发生的。
6、在两种媒质分界面的两侧,电场→E 的切向分量E 1t -E 2t =0;而磁场→B 的法向分量B 1n -B 2n =0。
7、在介电常数为e 的均匀各向同性介质中,电位函数为 2211522x y z ϕ=+-,则电场强度E=5x y zxe ye e --+。
8、静电平衡状态下,导体内部电场强度、磁场强度等于零,导体表面为等位面;在导体表面只有电场的法向分量。

电磁学答案第3章第三章 静电场的电介质3.2.1 偶极矩为p →=q l →的电偶极子,处于场强为E 的外电场中,p →与E →的夹角为θ。
(1) 若是均匀的,θ为什么值时,电偶极子达到平衡?(2)如果E 是不均匀的,电偶极子能否达到平衡? 解: (1)偶极子受的力:F + =F _=qE因而F →+=-F →_∴偶极子受合力为零。
偶极子受的力矩T =p ⨯E即 T=qEsin θ当 T=0时,偶极子达到平衡,∴ pEsin θ=0p →≠0 E →≠0 ∴θ=0 , πθ=0这种平衡是稳定平衡。
θ=π是不稳定平衡。
(2) 当E →不是均匀电场时,偶极子除受力矩外还将受一个 力(作用在两个点电荷的电场力的合力)。
所以不能达到平衡。
3.2.2 两电偶极子1p→和2p →在同一直线上,所以它们之间距r比它们自己的线度大的很多。
证明:它们的相互作用力的大小为F=402123rp p πε,力的方向是:1p→与2p→同方向时互相吸引,反方向时互相排斥。
证: 已知当r >>l 时,偶极子在其延长线上一点的场强:E →=302rpπε→当 1p →与2p →同方向时,如图2p →所受的力的大小:+→F =E →q=r lr q p ∧+3201)2(2πε-→F = -E→q=r lr q p ∧--3201)2(2πε∴F→= +→F +-→F =r l r l r q p ∧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+323201)2(1)2(12πε =r l r l l r q p ∧⎥⎦⎤⎢⎣⎡---⋅3222322201)2()2(2262πε略去 422l 及 832l 等高级小量。
F→=-r r qlp ∧402146πε= -r r pp ∧402123πε当 1p →与2p →反方向时(如图),同理: F→= r l r l r q p ∧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+323201)2(1)2(12πε =012πεq p ⨯r lr l l r ∧-+32223222)4()2(23略去高级小量得:F→=r rP P ∧402123πε3.2.3 一电偶极子处在外电场中,其电偶极矩为 ,其所在处的电场强度为 。


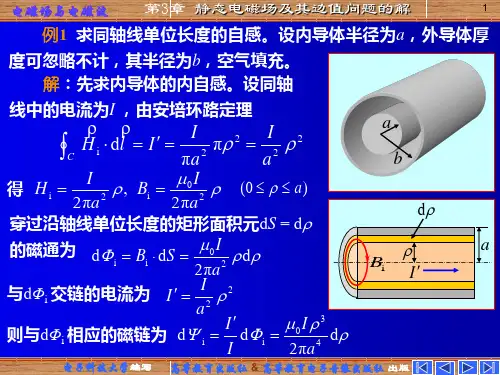

第3章 静态电磁场及其边值问题的解静态电磁场是电磁场的一种特珠形式。
当场源(电荷、电流)不随时间变化时,所激发的电场、磁场也不随时间变化,称为静态电磁场。
静止电荷产生的静电场、在导电媒质中恒定运动电荷形成的恒定电场以及恒定电流产生的恒定磁场都属于静态电磁场。
由麦克斯韦方程组可以看出,当场量不随时间变化时,电场矢量满足的方程和磁场矢量满足的方程是相互独立的,也就是说在静态情况下,电场和磁场是各自存在的,我们可以分别讨论。
本章将分别介绍静电场、恒定电场和恒定磁场的分析方法,最后介绍静电场边值问题的解法。
3.1 静电场分析静电场是静止电荷激发的,是电磁场的一种重要的和特珠的形式。
3.1.1 静电场的基本方程和边界条件1. 基本方程考虑到电磁场的源量(静止电荷q )和场量(E 、D )不随时间变化这一特征,由麦克斯韦方程组得出静电场的基本方程为积分形式d d (3.1.1)d 0(3.1.2)SV cVρ⎧=⎪⎨⎪=⎩⎰⎰⎰D S E l微分形式(3.1.3)0(3.1.4)ρ⎧∇⎪⎨∇⨯=⎪⎩D =E以及ε=D E (3.1.5)基本方程表明静电场是有源(通量源)无旋场,静止电荷是产生静电场通量源;电力线(E 线)从正的静止电荷发出,终于负的静止电荷。
2. 边界条件在两种电介质的分界面上,电场强度满足以下关系式()120n ⨯-=e E E 或 12t t E E = (3.1.6)表明电场强度的切向分量是连续的。
电位移矢量满足的关系式是()12n s ρ-=e D D 或 12n n s D D ρ-= (3.1.7)表明在两种媒质的分界面上存在自由面电荷分布时,电位移矢量的法向分量是不连续的。
若分界面上不存在面电荷,即0S ρ=,则()120n -=e D D 或 12n n D D = (3.1.8)此时,在分界面上,D 的法向分量是连续的。
式(3.1.8)可改写为1122n n E E εε=可见,当12εε≠时E 的法向分量是不连续的,这是因为分界面上存在束缚电荷密度。


电磁场理论基础第三版答案柯亨玉1.磁感应强度的单位是( ) [单选题] *A)T(正确答案)B)WbC)N/AD)Wb/m2.水的温度从17℃升高到100℃,用热力学温标表示,水温升高了( ) [单选题] *A)83K(正确答案)B)300KC)356KD)373K3.物体沿斜面匀速下滑,在此过程中物体的( ) [单选题] *A)机械能守恒B)机械能增加C)重力势能增加D)重力势能减少(正确答案)4.下列过程中,主要通过做功方式改变物体内能的是( ) [单选题] *A)湿衣服中的水蒸发B)水中的冰融化C)池水在阳光的照射下温度升高D)锤子敲击钉子后钉子变热(正确答案)5.直流电动机通电后,使线圈发生转动的力是( ) [单选题] *A)电场力B)磁场力(正确答案)C)万有引力D)重力6.在国际单位制中,属于基本单位的是 [单选题] *A)牛顿B)米(正确答案)C)特斯拉D) 焦耳7.电场强度的单位是 [单选题] *A) N/C(正确答案)(B) V/C(C) J/CD) T/C8.电子是原子的组成部分,一个电子带有 [单选题] *A) l.6×l0的-19次方C的正电荷(B) l.6×l0的-19次方C的负电荷(正确答案)(C) 9.l×l0的-31次方C的正电荷D) 9.l×l0的-31次方C的负电荷9.气体由无规则运动的分子组成,分子间有相互作用,因此气体的内能 [单选题] *A)仅包含分子动能B)仅包含分子势能C)与分子动能及分子势能无关D)包含分子动能及分子势能(正确答案)10.两个分子从相距很远(分子间作用力可忽略)变到很难靠近的过程中,表现为[单选题] *A)相互吸引B)相互排斥C)先排斥后吸引D)先吸引后排斥(正确答案)11.一杯水含有大量的水分子,若杯中水的温度升高,则( ) [单选题] *A)水分子的平均动能增大(正确答案)B)只有个别水分子动能增大C)抽有水分子的动能都增大D)每个水分子的动能改变量均相同12.下列物理量中,属于标量的是( ) [单选题] *A)功(正确答案)B)位移C)加速度D)电场强度13.静电场的电场线( ) [单选题] *A)可以相交B)是闭合的曲线C)起始于正电荷,终止于负电荷(正确答案)D)是点电荷在电场中运动的轨迹14.a、b和c三个带电小球,c带负电,a和b相互排斥,b和c相互吸引。
《电磁场理论》练习题与参考答案(最新版)第1~2章矢量分析宏观电磁现象的基本规律1. 设:直角坐标系中,标量场zx yz xy u ++=的梯度为A,则M (1,1,1)处A= ,=??A 0 。
2. 已知矢量场xz e xy e z y e A z y x ?4?)(?2+++= ,则在M (1,1,1)处=??A 9 。
3. 亥姆霍兹定理指出,若唯一地确定一个矢量场(场量为A),则必须同时给定该场矢量的旋度及散度。
4. 任一矢量场在无限大空间不可能既是无源场又是无旋场,但在局部空间可以有以及。
5. 写出线性和各项同性介质中场量D 、E 、B 、H、J 所满足的方程(结构方程):。
6. 电流连续性方程的微分和积分形式分别为和。
7. 设理想导体的表面A 的电场强度为E 、磁场强度为B,则(a )E 、B皆与A 垂直。
(b )E 与A 垂直,B与A 平行。
(c )E 与A 平行,B与A 垂直。
(d )E 、B 皆与A 平行。
答案:B8. 两种不同的理想介质的交界面上,(A )1212 , E E H H == (B )1212 , n n n n E E H H == (C)1212 , t t t t E E H H == (D) 1212 , t t n n E E H H == 答案:C9. 设自由真空区域电场强度(V/m) )sin(?0βz ωt E eE y -=,其中0E 、ω、β为常数。
则空间位移电流密度d J(A/m 2)为:222x y z e e e ++AA ??E J HB E Dσ=μ=ε= , ,t q S d J S ??-=?? t J ?ρ?-=?? 0A ??=0A ??=(a ))cos(?0βz ωt E ey - (b ))cos(?0βz ωt ωE e y -(c ))cos(?00βz ωt E ωey -ε (d ))cos(?0βz ωt βE e y -- 答案:C 10. 已知无限大空间的相对介电常数为4=εr ,电场强度(V/m) 2cos ?0dxeE x πρ=,其中0ρ、d 为常数。