下载文档原格式
2011年山东建筑大学工程力学课程考试复习题及参考答案一、填空题：1.受力后几何形状和尺寸均保持不变的物体称为__________________ 。
2.构件抵抗 _______________ 的能力称为强度。
3.圆轴扭转时，横截面上各点的切应力与其到圆心的距离成_____________ 比。
4.梁上作用着均布载荷，该段梁上的弯矩图为________________ 。
5.偏心压缩为 _________________________ 的组合变形。
6.柔索的约束反力沿 ___________________________ 离开物体。
7.构件保持 _______________ 的能力称为稳定性。
8.力对轴之矢 _____________________________________________ 情况下为零。
9.梁的中性层与横截面的交线称为________________ 。
10.图所示点的应力状态，其最大切应—_______________________________ 。
llOOMPa——100 MPa11.物体在外力作用下产生两种效应分别是_______________________________ 。
12.外力解除后可消失的变形，称为__________________ 。
13.力偶对任意点之矩都__________________ 。
14.阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和代弹性模量为E,则杆中最大正应力为___________________ 。
15.梁上作用集中力处，其剪力图在该位置有_____________ 。
16.光滑接触面约束的约束力沿__________________ 指向物体。
17.外力解除后不能消失的变形，称为___________________ 。
18.平面任意力系平衡方程的三矩式，只有满足三个矩心___________________ 的条件时，才能成为力系平衡的充要条件。
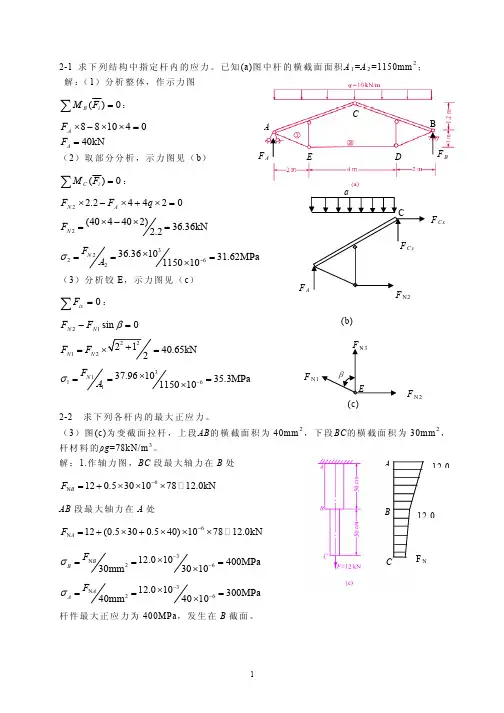
2-1 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2； 解：（1）分析整体，作示力图∑=0)(i BF M：CB 041088=××−×A F AF N1F N2(c)40kN A F =（2）取部分分析，示力图见（b ）∑=0)(i CF M：02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×（3）分析铰E ，示力图见（c ）∑=0ix F ：0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。
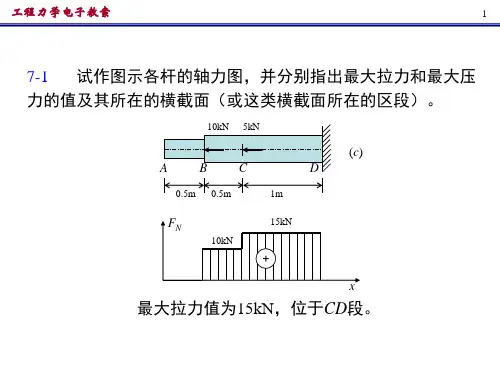
（3）图(c)为变截面拉杆，上段AB 的横截面积为40mm 2，下段BC 的横截面积为30mm 2，杆材料的ρg =78kN/m 3。
解：1.作轴力图，BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ，发生在B 截面。
EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm ，直径缩小了0.022mm ，确定材料的弹性模量E 、泊松比µ。
《工程力学2习题解答》建筑1001班陈飞力学教研室编著1-2. 试求图示结构mm 和nn 两截面上的内力，并指出AB 和BC 两杆属何种基本变形。
解：（1）求约束反力：取杆AB 为研究对象∑∑∑=⨯-⨯==-+===0233 003 000BCABCAAN M N Y Y X X 解得：kN Y kN N A BC 1 2==（2）求m-m 截面内力：将杆AB 沿截面m-m 截开, 取左半部分kNm Y M kN Y Q A m-m A m m 11 1=⨯===-AB 杆发生弯曲变形。
（3）求n-n 截面内力：取杆BC 为研究对象，截开n-n 截面kN N N BC n n 2==-BC 杆发生拉伸变形1-3. 拉伸试件A 、B 两点的距离l 称为标距，在拉力作用下，用引伸仪量出两点距离的增量为Δl =5×10-2mm 。
若l 的原长为l =10cm ，试求A 、B 两点间的平均应变。
解：平均应变为42105100105Δ--⨯=⨯==l l m ε1-4. 图示三角形薄板因受外力而变形。
角点B 垂直向上的位移为0.03mm ，但AB和BC 仍保持为直线。
试求沿OB 的平均应变，并求AB 、BC 两边在B 点夹角的变化。
解：（1） 求OB 方向的平均线应变n4105.212003.0Δ120-⨯=====l l mmOA OB m ε （2）求AB 与BC 两边的角应变4105.2'22-⨯=-=OB AO arctg πγ2-1. 试求图示各杆1-1、2-2、3-3截面的轴力， 并作轴力图。
解: (a)（1）求约束反力kNR R X 500203040 0==-++-=∑（2）求截面1-1的轴力kNN NR X 500011==+-=∑（3）求截面2-2的轴力kNN NR X 10040 022==++-=∑（4）求截面3-3的轴力(a) (b)kNN NR X 2003040 033-==+++-=∑（5）画轴力图(b)（1）求截面1-1的轴力01=N（2）求截面2-2的轴力 PN4022==（3）求截面3-3的轴力PN P P NX 304 033==-+=∑（4）画轴力图2-2. 作用图示零件上的拉力P=38kN ，试问零件内最大拉应力发生于哪个横截面上？并求其值。
第一章绪论一、选择题1．根据均匀性假设，可认为构件的（C）在各处相同。
A．应力B．应变C．材料的弹性系数D．位移2．构件的强度是指（C），刚度是指（A），稳定性是指（B）。
A．在外力作用下构件抵抗变形的能力B．在外力作用下构件保持原有平衡状态的能力C．在外力作用下构件抵抗强度破坏的能力3．单元体变形后的形状如下图虚线所示，则A点剪应变依次为图(a) （A），图(b) （C），图(c) （B）。
A．0B．r2C．r D．1.5r4.下列结论中( C )是正确的。
A．内力是应力的代数和；B．应力是内力的平均值；C．应力是内力的集度；D．内力必大于应力；5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力，它们的应力是否相等（B）。
A．不相等；B．相等；C．不能确定；6．为把变形固体抽象为力学模型，材料力学课程对变形固体作出一些假设，其中均匀性假设是指（C）。
A. 认为组成固体的物质不留空隙地充满了固体的体积；B. 认为沿任何方向固体的力学性能都是相同的；C. 认为在固体内到处都有相同的力学性能；D. 认为固体内到处的应力都是相同的。
二、填空题1.材料力学对变形固体的基本假设是连续性假设，均匀性假设，各向同性假设。
2．材料力学的任务是满足强度，刚度，稳定性的要求下，为设计经济安全的构件提供必要的理论基础和计算方法。
3．外力按其作用的方式可以分为 表面力 和 体积力 ，按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。
4．度量一点处变形程度的两个基本量是 （正）应变ε 和 切应变γ。
三、判断题1．因为构件是变形固体，在研究构件平衡时，应按变形后的尺寸进行计算。
（ × ） 2．外力就是构件所承受的载荷。
（ × ） 3．用截面法求内力时，可以保留截开后构件的任一部分进行平衡计算。
（ √ ） 4．应力是横截面上的平均内力。
（ × ） 5．杆件的基本变形只是拉(压)、剪、扭和弯四种，如果还有另一种变形，必定是这四种变形的某种组合。
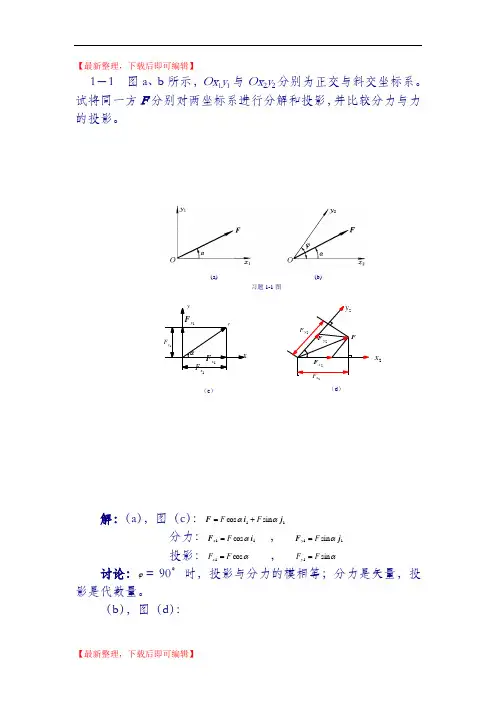
(a) (b)习题1-1图 【最新整理，下载后即可编辑】1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
解：（a ），图（c ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（d ）：1y F x xF 1y Fα1xF y F（c ）2F2y F2y2x 2x F2y FF（d ）(a) (b)习题1－2图F DR AC BD AxF AyF(a-1)Ay F FB C A AxF 'F C(a-2) C DF DR(a-3)AxFF A C BD AyF (b-1) 分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j FϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。
比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。
1－3 试画出图示各物体的受力图。
习题1－3图F AxFAyF D C BABF或(a-2)FB AF DCA(a-1)BF AxF AAyF C(b-1)WF BD CF FCBBF AACBF(f-1)(e-3)'A(f-2)1O(f-3)c FF AF DF BF AF A习题1－4图1－4 图a所示为三角架结构。
力F1作用在B铰上。
杆AB 不计自重，杆BD杆自重为W。
试画出图b、c、d所示的隔离体的受力图，并加以讨论。
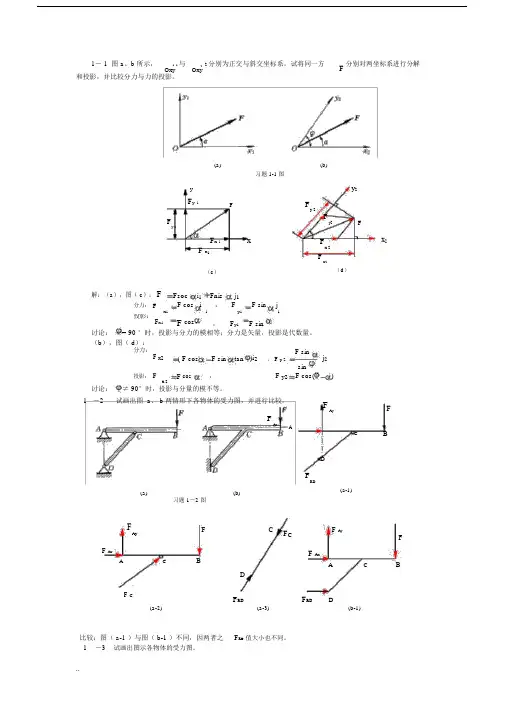
1－ 1 图 a 、b 所示，1 1与22分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解OxyOxy和投影，并比较分力与力的投影。
(a) (b)习题 1-1 图yy 2F y 1FFy 2FFy 1Fy 2F x 1xFx 2x 2F x 1Fx 2（c ）（d ）解：（a ），图（ c ）： FFsoc i 1 Fnis j 1分力： Fx1 F cos i 1 ， F y1 F sinj1投影：F x1F cos， F y1 F sin讨论：= 90 °时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（ d ）：分力： F x2 ( F cosF sin tan )i 2 F sinj 2， F y 2sin投影： FF cos ，F y2 F cos()x 2讨论： ≠ 90°时，投影与分量的模不等。
1 －2试画出图 a 、 b 两情形下各物体的受力图，并进行比较。
FAyFAxACDFRDFB(a)(b)(a-1)习题 1－2 图FAyFCF CF AyFF AxF AxACBA CBD'F CF RDF RDD(a-2)(a-3)(b-1)比较：图（ a-1 ）与图（ b-1 ）不同，因两者之 F R D 值大小也不同。
1 －3 试画出图示各物体的受力图。
..习题 1－3 图FDCFDC CBFF BAFAxABFAxBAF AF BFAyF BFAy(a-1)或(a-2)(b-1)CB FBDF DCF BF BABWFAxCAF AF AFAyD或(b-2) (c-1)(d-1)F CDFFCCFAxABCF cAFAyDF ABF AF D(e-1)F B或(d-2) F D(e-2)D FF O 1'CF AF O 1AF OxAFOxOOO 1FOyFOyABF AF AA ..WF B W(f-2)(e-3)(f-1)(f-3)F AF AF B1 －4 图 a 所示为三角架结构。
