五年级奥数-容斥原理

點算的奧秘：容斥原理基本公式「容斥原理」(Principle of Inclusion and Exclusion)(亦作「排容原理」)是「點算組合學」中的一條重要原理。

但凡略為複雜、包含多種限制條件的點算問題，都要用到這條原理。

現在首先從一個點算問題說起。

例題1：設某班每名學生都要選修至少一種外語，其中選修英語的學生人數為25，選修法語的學生人數為18，選修德語的學生人數為20，同時選修英語和法語的學生人數為8，同時選修英語和德語的學生人數為13 ，同時選修法語和德語的學生人數為6，而同時選修上述三種外語的學生人數則為3，問該班共有多少名學生？答1：我們可以把上述問題表達為下圖：其中紅色、綠色和藍色圓圈分別代表選修英語、法語和德語的學生。

根據三個圓圈之間的交叉關係，可把上圖分為七個區域，分別標以A至G七個字母。

如果我們用這七個字母分別代表各字母所在區域的學生人數，那麼根據題意，我們有以下七條等式：(1) A+D+E+G = 25；(2) B+D+F+G = 18；(3) C+E+F+G = 20；(4) D+G = 8； (5) E+G = 13；(6) F+G = 6；(7) G = 3。

現在我們要求的是A+B+C+D+E+F+G。

如何利用以上資料求得答案？把頭三條等式加起來，我們得到A+B+C+2D+2E+2F+3G = 63。

可是這結果包含了多餘的D、E、F和G，必須設法把多餘的部分減去。

由於等式(4)－(6)各有一個D、E和F，若從上述結果減去這三條等式，便可以把多餘的D、E和 F減去，得A+B+C+D+E+F = 36。

可是這麼一來，本來重覆重現的G卻變被完全減去了，所以最後還得把等式(7)加上去，得最終結果為A+B+C+D+E+F+G = 39，即該班共有39名學生。

□在以上例題中，給定的資料是三個集合的元素個數以及這些集合之間的交集的元素個數。

在該題的解答中，我們交替加上及減去這些給定的資料。

容斥原理学生姓名授课日期教师姓名授课时长知识定位容斥原理中的知识点比较简单,是计数问题中比较浅的一支。

这个知识点经常和数论知识结合出综合型题目。

这个原理本身并不是很难理解,不过经常和数论知识结合出题,所以对学生的理解层次要求较高,学生必须充分理解、吃透。

1.充分理解和掌握容斥原理的基本概念2.利用图形分析解决容斥原理问题知识梳理授课批注：本讲的知识点必须让学生充分理解、吃透,这个原理本身并不是很难理解,不过经常和数论知识结合出题所以对学生的理解层次要求较高。

一. 容斥原理的概念定义在一些计数问题中,经常遇到有关集合元素个数的计算。

我们用|A|表示有限集A 的元素个数。

求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成：|A∪B| = |A| + |B| - |A∩B|,我们称这一公式为包含与排除原理,简称容斥原理。

图示如右:A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为：A∩B,即阴影面积。

用法：包含与排除原理告诉我们,要计算两个集合A、B的并集A∪B的元素的个数,可分以下两步进行：第一步：分别计算集合A、B的元素个数,然后加起来,即先求|A|+|B|（意思是把A、B的一切元素都“包含”进来,加在一起）；第二步：从上面的和中减去交集的元素个数,即减去C=|A∩B|（意思是“排除”了重复计算的元素个数）二.竞赛考点1. 容斥原理的基本概念2. 与数论相结合的综合型题目例题精讲【试题来源】【题目】在一个炎热的夏日,10个小学生去冷饮店每人都买了冷饮。

其中6人买了汽水,6人买了可乐,4人买了果汁,有 3人既买了汽水又买了可乐,1人既买了汽水又买了果汁,2人既买了可乐又买了果汁。

问：(1)三样都买的有几人？(2)只买一样的有几人？【试题来源】【题目】某班有学生46人,在调查他们家中是否有电子琴和小提琴时发现,有电子琴的22人,两种琴都没有的14人,只有小提琴的与两种琴都有的人数之比是5∶3。

五年级奥数培训资料—容斥原理班级：姓名：策略思想：在生活中我们经常会碰到有些数量会出现重复、包含的情况，那么在解题时就要考虑排除由于重复、相互包含而引起的多加的情况，这就是包含与排除问题，也称容斥原理。

解题要点：解答重叠问题时首先要确定采用哪种分类标准，然后根据题意画出图示，找出哪些是重复的，重复了几次，仔细审题，明确求的哪部分，再根据包含与排除原理进行解题。

例题1：五（3）班每个人都订阅了学习报（数学报、语文报），订阅《小学生数学报》的有30人，订阅《小学生语文报》的有26人。

两种都订阅的有14人，这个班有学生多少人？练习1：五（3）班每人都参加了课外兴趣小组（舞蹈、合唱），参加舞蹈队的有21人，参加合唱团的有32人，既参加舞蹈队的又参加合唱团的有9人，全班共有多少人？练习2：一个班有45个小学生,统计借课外书的情况是:全班学生都借有语文或数学课外书.借语文课外书的有39人,借数学课外书的有32人.语文、数学两种课外书都借的有多少人？例题2：47名学生参加数学和语文考试，其中语文得100分的有12人，数学得100分的有17人，两门都没得100分的26人，两门都得100分的有多少人？练习1：六（1）班有学生46人,其中会骑自行车的17人,会游泳的14人,既会骑车又会游泳的4人,问两样都不会的有多少人？练习2：音乐班有40名学生，25名学生会作曲，20人会指挥，有10人作曲和指挥都不会，既会作曲、又会指挥的学生有多少人？例题3：在一个炎热的夏日，有一群小朋友去冷饮店每人都买了冷饮。

其中6人买了汽水，6人买了可乐，4人买了果汁，有3人既买了汽水又买了可乐，1人既买了汽水又买了果汁，2人既买了可乐又买了果汁，三种冷饮都买了的有1人，一共有几个小朋友？练习1：一批教师，每人至少都会一门外语，会英语的有65人，会俄语的有58人，会日语的有51人，既会英语又会俄语的有21人，既会英语又会日语的有19人，既会俄语又会日语的有17人，三种都会的有5人。

容斥原理（一）
森林里住着100只小白兔，凡是不爱吃萝卜的小白兔都爱吃白菜。

其中爱吃萝卜的小白兔数量是爱吃白菜的小白兔数量的2倍，而不爱吃白菜的小白兔数量是不爱吃萝卜的小白兔数量的3倍。

它们当中有多少只小白兔既爱吃萝卜又爱吃白菜？
有100位旅客，其中有10人既不懂英语，又不懂俄语，有75人懂英语，又83人懂俄语。

那么这100位旅客中既懂英语又懂俄语的有多少人。

在1至2011的自然数中，
⑴能被3或5或7整除的数有个；
⑵能同时被3，5，7整除的有个；
⑶能被3整除，但不能被5和7整除的有个；
⑷能被5和7整除，但不能被3整除的有个。

体育课上，60名学生面向老师站成一行，按老师口令，从左到右报数：1，2，3， (60)
然后，老师让所报的数是4的倍数的同学向后转，接着又让所报的数是5的倍数的同学向后转，最后让所报的数是6的倍数的同学向后转，现在面向老师的学生有________人。

中国田径队的40名运动员在训练基地进行封闭训练，其中男运动员有20名，训练长跑的运动员有15名，训练竞走的女运动员有8名，那么训练长跑的男运动员有多少名？。

小学数学五年级下册奥数思维—容斥原理知识点解析：容斥问题涉及到一个重要原理——包含与排除原理，也叫容斥原理。

即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。

容斥原理：对n个事物，如果采用不同的分类标准，按性质a分类与性质b分类（如图），那么具有性质a或性质b 的事物的个数=Na＋Nb－Nab。

例1：一个班有48人，班主任在班会上问：“谁做完语文作业？请举手！”有37人举手。

又问：“谁做完数学作业？请举手！”有42人举手。

最后问：“谁语文、数学作业都没有做完？”没有人举手。

求这个班语文、数学作业都完成的人数。

例2：某班有36个同学在一项测试中，答对第一题的有25人，答对第二题的有23人，两题都答对的有15人。

问多少个同学两题都答得不对？例3：某班有56人，参加语文竞赛的有28人，参加数学竞赛的有27人，如果两科都没有参加的有25人，那么同时参加语文、数学两科竞赛的有多少人？例4：在1到100的自然数中，既不是5的倍数也不是6的倍数的数有多少个？例5：光明小学举办学生书法展览。

学校的橱窗里展出了每个年级学生的书法作品，其中有24幅不是五年级的，有22幅不是六年级的，五、六年级参展的书法作品共有10幅，其他年级参展的书法作品共有多少幅？1.分析与解答完成语文作业的有37人，完成数学作业的有42人，一共有37＋42=79人，多于全班人数。

这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次，在统计做完数学作业的人数时又算了一次，这样就多算了一次。

所以，这个班语文、数作业都完成的有：79－48=31人。

2.分析与解答：已知答对第一题的有25人，两题都答对的有15人，可以求出只答对第一题的有25－15=10人。

又已知答对第二题的有23人，用只答对第一题的人数，加上答对第二题的人数就得到至少有一题答对的人数：10＋23=33人。

所以，两题都答得不对的有36－33=3人。

第33讲包含与排除（容斥原理）一、知识要点集合是指具有某种属性的事物的全体，它是数学中的最基本的概念之一。

如某班全体学生可以看作是一个集合，0、1、2、3、4、5、6、7、8、9便组成一个数字集合。

组成集合的每个事物称为这个集合的元素。

如某班全体学生组成一个集合，每一个学生都是这个集合的元素，数字集合中有10个元素。

两个集合中可以做加法运算，把两个集合A、B合并在一起，就组成了一个新的集合C。

计算集合C的元素的个数的思考方法主要是包含与排除：先把A、B的一切元素都“包含”进来加在一起，再“排除”A、B两集合的公共元素的个数，减去加了两次的元素，即：C=A ＋B－AB。

在解包含与排除问题时，要善于使用形象的图示帮助理解题意，搞清数量关系的逻辑关系。

有些语言不易表达清楚的关系，用了适当的图形就显得很直观、很清楚，因而容易进行计算。

二、精讲精练例1 五年级96名学生都订了报纸，有64人订了少年报，有48人订了小学生报。

两种报纸都订的有多少人？分析用左边的圆表示订少年报的64人，右边的圆表示订小学报的48人，中间重叠部分表示两种报刊都订的人数。

显然，两种报刊都订的人数被统计了两次：64＋48=112人，比总人数多112－96=16人，这16人就是两种报刊都订的人数。

练习一1，一个班的52人都在做语文和数学作业。

有32人做完了语文作业，有35人做完了数学作业。

语文、数学作业都做完的有多少人？2，五年级有122人参加语文、数学考试，每人至少有一门功课得优。

其中语文得优的有65人，数学得优的有87人。

语文、数学都得优的有多少人？3，某班有50名学生，在一次测验中有26人满分，在第二次测验中有21人满分。

如果两次测验都没得过满分的学生有17人，那么，两次测验都得满分的有多少人？例2：某校教师至少懂得英语和日语中的一种语言。

已知有35人懂英语，34人懂日语，两种语言都懂的有21人。

这个学校共有多少名教师？分析把懂英语和懂日语的人数加起来得35＋34=69人，但是，两种语言都懂的21人被统计过两次，应该从69里去掉一个21才能得出这个地区外语教师的总人数：69－21=48人。

第十二讲容斥原埋在很多计数问题中常用到数学上的一个包含与排除原理，也称为容斥原理.为了说明这个原理，我们先介绍一些集合的初步知识。

在讨论问题时，常常需要把具有某种性质的同类事物放在一起考虑.如：A=｛五（1）班全体同学｝.我们称一些事物的全体为一个集合.A＝{五（1）班全体同学}就是一个集合。

例1 B＝｛全体自然数｝=｛1，2，3，4，…｝是一个具体有无限多个元素的集合。

例2 C=｛在1，2，3，…，100中能被3整除的数｝＝（3，6，9，12，…，99｝是一个具有有限多个元素的集合。

集合通常用大写的英文字母A、B、C、…表示.构成这个集合的事物称为这个集合的元素.如上面例子中五（1）班的每一位同学均是集合A的一个元素.又如在例1中任何一个自然数都是集合B的元素.像集合B这种含有无限多个元素的集合称为无限集.像集合C这样含有有限多个元素的集合称为有限集.有限集合所含元素的个数常用符号|A|、|B|、|C|、…表示。

记号A∪B表示所有属于集合A或属于集合B的元素所组成的集合.就是右边示意图中两个圆所覆盖的部分.集合A∪B叫做集合A与集合B 的并集.“∪”读作“并”，“A∪B”读作“A并B”。

例3 设集合A=｛1，2，3，4｝，集合B=｛2，4，6，8｝，则A∪B=｛1，2，3，4，6，8｝.元素2、4在集合A、B中都有，在并集中只写一个。

记号A∩B表示所有既属于集合A也属于集合B中的元素的全体.就是上页图中阴影部分所表示的集合.即是由集合A、B的公共元素所组成的集合.它称为集合A、B的交集.符号“∩”读作“交”，“A∩B”读作“A交B”.如例3中的集合A、B，则A∩B=｛2，4｝。

下面再举例介绍补集的概念。

例4 设集合I=｛1，3，5，7，9｝，集合A=｛3，5，7｝。

补集（或余集），如图中阴影部分表示的集合（整个长方形表示集合I）.对于两个没有公共元素的集合A和B，显然有|A∪B|=|A|+|B|。

容斥原理1、五年级（1）班有学生56人，其中45人完成数学作业，42人完成语文作业，这个班两种作业都做完的有多少人？2、某校挑选18名学生参加春季运动会，获一等奖的有12人，获二等奖的有11人，两个奖都取得的有9人，这次运动会上两个奖都没取得的有多少人？3、在1-100的全部自然数中，不是3的倍数也不是5的倍数的数有多少个？4、某学校组织同学参加足球和乒乓球比赛，参加足球比赛的有20人，参加乒乓球比赛的有18人，同时参加足球和乒乓球比赛的有13人，问参加比赛的共有多少人？5、某班有46人，其中会骑车的有17人，会游泳的有14人，既会骑车又会游泳的有5人，问两样都不会的有几人？6、某班共有45人，其中有35人会用电脑打字，这个班有男生23人，女生中有6人不会用电脑打字，那么男生中有多少人会用电脑打字？7、五（1）班有40名学生，参加围棋班的有15人，参加电脑班的有11人，参加美术班的有13人，同时参加围棋和电脑班的有4人，同时参加围棋和美术班的有5人，同时参加美术和电脑班的有5人呢，班上有3人三个班都参加了，问班级中没有参加兴趣班的有多少人？8、在一根长的木棍上有三种刻度线，第一种刻度线，将木棍10等分，第二种刻度线将木棍12等分，第三种刻度线将木棍15等分。

如果沿每条刻度线将木棍锯断，木棍总共被锯成多少段？创新题1、一个班有45个小学生，统计借课外书的情况是：全班学生都借有语文或数学课外书，借语文课外书的有39人，借数学课外书的有32人，语文、数学两种课外书都借的有多少人？2、在1-100的所有自然数中，既非3的倍数也不是4或5的倍数的数有多少个？3、80个外语老师中，懂英语的有65人，懂日语的有35人，其中必有既懂英语又懂日语的的老师，问只懂英语的老师有多少人？4、五年级某班学生进行百米跑、跳远、投掷3个项目的测试，跳远达到优秀的有28人，投掷达到优秀的有26人，百米跑达到优秀的有24人，百米跑和跳远都达优的有12人，跳远和投掷达优的有9人，百米跑和投掷都达优的有14人，3项都达优的有5人，这个班有多少位同学？单元测试题1、某班有50名学生，在第一次测验中有26人得满分，在第二次测验中有21 人得满分，如果两次测验都没得过满分的学生有17人，那么两次测验都活得满分的有多少人？2、第一小组的同学们都在做两道练习题，做对第一题的有15人，做对第二题的有10人，两题都做对的有7人，两题都做错的有2人，第一小组一共有多少人？3、问1-1000中所有不能被6,8,10整除的自然数有多少个？4、某校100个老师懂英语或法语，其中懂英语的有75人，既懂英语又懂法语的有20人，问懂法语的有多少人？只懂法语的有多少人？5、五年级112名同学参加语文、数学考试，没人至少有一门获优，已知语文获优者60人，数学获优者73人，求只有语文一门获优的人数.6、五一班有56名同学，只会打乒乓球的有28人，会打乒乓球又会打羽毛球的有16人，只会打羽毛球的有多少人？7、在1,2,3，、、、，1998这1998个数中，既不是8的倍数，又不是12的倍数的数共有多少个？。

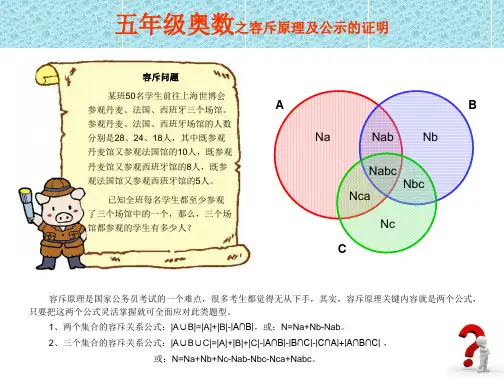
容斥原理在计数时，为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

容斥原理（1）如果被计数的事物有A、B两类，那么，A类或B类元素个数= A类元素个数+B类元素个数—既是A类又是B类的元素个数。

例1一次期末考试，某班有15人数学得满分，有12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？分析：依题意，被计数的事物有语、数得满分两类，“数学得满分”称为“A类元素”，“语文得满分”称为“B类元素”，“语、数都是满分”称为“既是A类又是B类的元素”，“至少有一门得满分的同学”称为“A类或B类元素个数”的总和。

试一试：某班学生每人家里至少有空调和电脑两种电器中的一种，已知家中有空调的有41人，有电脑的有34人，二者都有的有27人，这个班有学生多少人？（并说一说你的想法。

）容斥原理（2）如果被计数的事物有A、B、C三类，那么，A类或B类或C类元素个数= A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数1、某艺术团的小演奏家们每人都至少会演奏小提琴和钢琴中的一种。

他们中有32人会拉小提琴，27人会弹钢琴，小提琴和钢琴都能演奏的有11人。

这个团共有多少个小演奏家？2、一个班有学生42人，参加体育队的有30人，参加文艺队的有25人，并且全班每人至少参加一个队。

问：这个班两队都参加的有多少人？3、京华小学五年级学生采集标本。

采集昆虫标本的有25人，采集植物标本的有19人，两种标本都采集的有8人。

全班学生共有40人，没有采集标本的有多少人？4、有100位旅客，其中有10人既不懂英语又不懂日语，有75人懂英语，83人懂日语。

容斥原理（二）【例2】(★★★★)【例1】(★★★)唐僧西天取经共经历了81难，其中单独度过了3难，与孙悟空一起度过了77难，与猪八戒一起度过了65难，与沙和尚一起度过了62难，同时与孙悟空和猪八戒一起度过了64难，同时与孙悟空和沙和尚一起度过了61难，同时与猪八戒和沙和尚一起度过了60难。

请问：师徒四人共同度过的有多少难？某班人数60人，在一次抽考英语、数学、化学的考试中，英语及格的有41人，数学及格的有39人，化学及格的有42人；英语、数学两科不及格的有14人，数学、化学两科不及格的有13人，英语、化学两科不及格的有11人，有两科或两科以上不及格的人数为20人，则：⑴三科都不及格的有几人？⑵至少有一科不及格的有几人？⑶三科都及格的人数有几人？【例3】(★★★★)五年级一班有46名学生参加数学、语文、文艺三项课外小组。

其中有24人参加了数学小组，20人参加了语文小组，既参加数学小组又参加语文小组的有10人.参加文艺小组的人数是既参加数学小组又参加文艺.，，也参加语文小组的人数等于三项小组都参加的人数的2倍，求参加文艺小组的人数。

【例4】(★★★)六年级⑴班有32人参加数学竞赛，有27人参加英语竞赛，有22人参加语文竞赛，其中参加了数学和英语的有12人，参加了英语和语文的有14 人，参加了数学和语文的有10人，那么六年级⑴班全班至少有多少人？【例5】(★★★)甲、乙、丙三人都在读同一本故事书，书中有100个故事。

已知甲读了85个故事，乙读了70个故事，丙读了62个故事。

请问：甲、乙、丙三人共同读过的故事最少有多少个？1【例6】(★★★★★)在阳光明媚的一天下午，甲、乙、丙、丁四人给100盆花浇水，已知甲浇了30盆，乙浇了75盆，丙浇了80盆，丁浇了90盆，请问恰好被3个人浇过的花最少有多少盆？一、本讲重点知识回顾1．基本原理⑴二者容斥⑵三者容斥【例7】(★★★)中国田径队的40名运动员在训练基地进行封闭训练，其中男运动员有20名，训练长跑的运动员有15名，训练竞走的女运动员有8名，那么训练长跑的男运动员有多少名？C A BCA B C A B B C A CA B C2．口诀：奇层加，偶层减3．解题技巧：画图——文氏图，线段图方程列表高斯记号应用——取整运算答案【例1】59难【例3】21人【例2】⑴9人⑵29人⑶31人【例4】47人二、本讲经典例题容斥原理㈠：例1，例2，例5，例6 【例5】17个【例6】15盆容斥原理㈡：例１，例３，例６，例7【例7】3名2。

五年级奥数容斥问题：容斥原理（1）如果被计数的事物有a、b两类，那么，a类或b类元素个数= a类元素个数+b类元素个数—既是a类又是b类的元素个数。

容斥原理（2）如果被计数的事物有a、b、c三类，那么，a类或b类或c类元素个数= a类元素个数+b类元素个数+c类元素个数—既是a类又是b类的元素个数—既是a类又是c类的元素个数—既是b类又是c类的元素个数+既是a类又是b类而且是c类的元素个数1、艺术小学举行学生画展，其中18幅画不是六年级的，20幅画不是五年级的，现在知道五、六年级共展出22幅画。

问其他年级展出多少幅？分析：18幅不是六年级，那就是五年级和其他年级的，20幅不是五年级，就是六年级和其他年级，已知五六年级展出22幅，所以其他年级展出就是八幅。

（18+20-22）/2=8（幅）2、某地区100个外语教师中，每人至少懂英语和日语中的一种语言。

已知懂英语的75人，懂日语的有45人。

问只懂英语的有几人？分析；两种语言都懂的人为；懂英语的和懂日语和减外语教师总数。

只懂英语的就是75减两种都懂得了。

75+45-100=20（人）75-20=55（人）3、在1至100的整数中,能被2整除或能被3整除的数共有几个?分析：100中，能被2整除的有100/2=50个，能被3整除的有100/3=33个，同时能被2和3整除的100/6=16个，注意这16个包括在能被2和3整除的，要去掉。

就是100内能被或3整除的。

50+33-16=67个4、全班50人，不会骑自行车的有23人，不会滑旱冰的有35人，两样都会的有4人，两样都不会的有多少人？分析：骑自行车：27人会滑旱冰：15人都会：4人都不会的：50-（27+15-4）=12人画个图就可以看出来了，4个人是多加的，所以要减去。

5、六年级有52人，其中喜欢绘画的36人，喜欢书法的有42人，喜欢唱歌的有48人，喜欢跳舞的有34人，这个班最少有多少学生对这四项活动都喜欢？分析：52-36=16个人不喜欢绘画，52-42=10个人不喜欢书法，52-48=4个人不喜欢唱歌，52-34=18个人不喜欢跳舞。