第七讲:多面体与旋转体
- 格式:doc
- 大小:781.00 KB
- 文档页数:7
课题认识多面体与旋转体主备张教师教课课时1课时备课时间教课目的知识与能力过程与方法感情、态度、价值观理解多面体的有关观点;理解旋转体的有关观点。
能依据几何构造特点对空间物体进行分类。
感觉空间实物及模型,增强学生的直观感知。
教课要点多面体与旋转体的有关观点教课难点依据几何构造对空间物体的分类教课准备(包含课件、挂图、资料采集等)教课过程师生互动设计企图一、新课导入小学和初中我们学过平面上的一些几何图形如直线、师:回想前方从生活实质三角形、长方形、圆等等,现实生活中,我们四周还存在学过的几何图形有问题引入,惹起学生着好多不是平面上而是“空间”中的物体,它们占有着空哪些的兴趣。
间的一部分,比方粉笔盒、足球、易拉罐等. 假如只考虑这些物体的形状和大小,那么由这些物体抽象出来的空间图形叫做空间几何体 . 它们拥有千姿百态的形状,有着不一样的几何特点,此刻就让我们来研究它们吧!二、研究新知研究 1:多面体的有关观点教师发问,学在研究中学习知生回答下列问题,教师识,切合现代教课理总结。
念。
新知 1:由若干个平面围成的几何体几何体叫做多面体 . 围成每个多面体的多边形叫做多面体的面,如面ABCD;两个面的公共边叫多面体的棱,如棱 AB;棱和棱的公共点叫多面体的极点,如极点 A. 连接不在同一平面上的两个极点的线段叫做多面体的对角线,详细以下列图所示:顶D C点A B面棱CA B教师给出题掌握定义,培育目,学生疏组回答。
学合作意识。
研究 2:旋转体的有关观点教师发问,学在研究中学习知生回答下列问题,教师识,切合现代教课理总结。
念。
新知 2:由一条平面曲线绕一条定直线旋转所形成的曲面叫旋转面,关闭的旋转面围成的几何体叫做旋转体,这条定直线叫旋转体的轴 . 这条曲线叫做旋转体的母线。
以下列图的旋转体 :教师给出题在研究中学习知目,学生疏组回答。
识,切合现代教课理念。
四、讲堂小结1、多面体的观点及有关知识2、旋转体的观点及有关知识板书设计1、多面体:面、棱、极点、对角线;2、旋转体:旋转面、轴、母线作业设计手工制作:本节课课本上出现的几何体或自由制作。

《多面体与旋转体》知识点1、多面体:(1)棱柱的主要性质:①棱柱的所有侧棱都 ,直(正)棱柱的侧棱长等于 。
②棱柱的每一个侧面都是 形,直棱柱的每一个侧面都是形,正棱柱的各个侧面都是 形。
③棱柱中,过不相邻的两条侧棱的截面都是 形。
(2)填适当的符号,表示下列集合之间的关系:四棱柱 平行六面体 直平行六面体 长方体 正四棱柱 正方体(3)长方体中过一个顶点的三条棱长分别为a 、b 、c,则它的对角线长d= 。
(4)棱锥:① 叫做正棱锥。
②正棱锥各侧棱 ,各侧面是全等的 ,③s s 棱锥截棱锥底=④正棱锥的 、 和 组成一个直角三角形;正棱锥的高、侧棱、侧棱在底面的摄影也组成一个 。
(5)面积,体积公式:s 直棱柱侧= , v 棱柱= ,s 正棱锥侧= , v 棱锥= , 2、旋转体:(1)圆柱:平行于底面的截面是 ,轴截面是 ,s 轴截面= ,(2)圆锥:h, r, l 之间的关系式: 。
s s 圆锥截圆锥底= ,轴截面是 ,s 轴截面= ,(3)圆柱侧面展开图是 ,圆锥侧面展开图是 , s 圆柱侧= = , s 圆柱全= ,v 圆柱= , s 圆锥侧= = , s 圆锥全= ,v 圆锥= ,(4)球:①截面是 ,d, R, r, 之间的关系式 ,②球面上两点的距离:经过两点的大圆在这两点间的一段 的长度。
③ S 大圆= S 球= ,V 球=选择题:1、斜四棱柱的侧面为矩形的个数最多有 ( )A O 个B 1个C 2 个 D3个 2、若棱住的侧面是全等的矩形,则棱柱是( )A .直棱柱B .正棱柱C .正方体D .底面为菱形的直棱柱 3、若长方体的三条棱长分别是3、5、15,则长方体的对角线的长是( ) A .53 B 23 C .3 D .不同于以上答案 4、若两球的表面积之比为1:2,则其半径之比为( )A 1:2B 1:4C 1:2D 1:22 5、侧棱长为2,底面周长为3的正三棱锥的高是( )A .311 B .313 C .339 D .333 6、各棱长均为1的正三棱锥的全面积为 ( )A .2B .3C .2D .367、已知圆柱的轴截面是一个面积为4的正方形,则圆柱的侧面积是( )A .π2B .π4C .π6D .π8 8、圆锥侧面展开图是半径为a 的半圆,这个圆锥的高是( )A .aB .a 22 C .a 3 D .a 23 9、正方体的对角线长为L ,它的全面积是 ( )A .2L 2B .32L C .12L 2 D .18L 210、圆柱的一个底面面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是( ) A 4πS B 2πS C πS D 3πS11、轴截面为直角三角形的圆锥,侧面积与底面积之比为 ( )A 2:1B 3:1C 5:1D 2:1 12、正四棱锥底面边长为2,侧面积为8,它的体积为( )A334 B 23 C 43 D 83 13、若球的体积增大为原来的8倍,则它的表面积增大为原来的 ( )A2倍 B 4倍 C8倍 D16倍14、一个棱锥的底面面积为Q ,过它的高的中点作平行于底面的截面,那么截面面积 ( )A21Q B 31Q C 41Q D 22Q 15、各棱长均相等的正四棱锥的侧面与底面所成的二面角的余弦值为 ( )A63 B 33 C 23 D 36二、填空题:1、正方体一个面的对角线的长为a ,则正方体的对角线长是__________。


多面体与旋转体一、棱柱1、 由几个多边形围成的封闭的几何体叫做多面体。
2、 两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱。
棱柱的互相平行的两个面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻的两个侧面的公共边叫做棱柱的侧棱,两个底面间的距离叫做棱柱的高。
棱柱的基本性质:(1) 棱柱的侧面都是平行四边形。
(2) 棱柱的两个底面及平行于底面的截面都是全等的多边形。
3、 侧棱与底面不垂直的的棱柱叫做斜棱柱。
侧棱与底面垂直的棱柱叫做直棱柱。
底面是正多边形的直棱柱叫做正棱柱。
性质:(1) 直棱柱侧面都是矩形。
(2) 直棱柱侧棱与高相等。
(3) 正棱柱的侧面都是全等的矩形。
4、 底面是平行四边形的棱柱叫做平行六面体。
底面是矩形的直棱柱是长方体。
长方体的对角线平方等于三边长的平方和。
5、 夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任何平面所截得的两个截面的面积都相等,那么这两个几何体的体积相等。
6、 h V S =⋅棱柱底. 二、棱锥1、有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
棱锥的这个多边形的面叫做底面,其余各个三角形的面叫做侧面。
相邻的两个侧面的公共边叫做棱锥的侧棱。
各个侧面的公共顶点叫做棱锥的顶点,顶点到底面的距离叫做棱锥的高。
棱锥的基本性质:如果一个棱锥被平行于底面的一个平面所截,那么: (1) 侧棱和高被这个平面分成比例线段; (2) 截面和底面都是相似多边形;(3) 截面面积与底面面积之比,等于顶点到截面与顶点到底面的距离平方之比。
2、如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,这个棱锥叫做正棱锥。
正棱锥的性质:(1) 各侧棱相等,各侧面都是全等的等腰三角形。
(2) 正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形。
正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
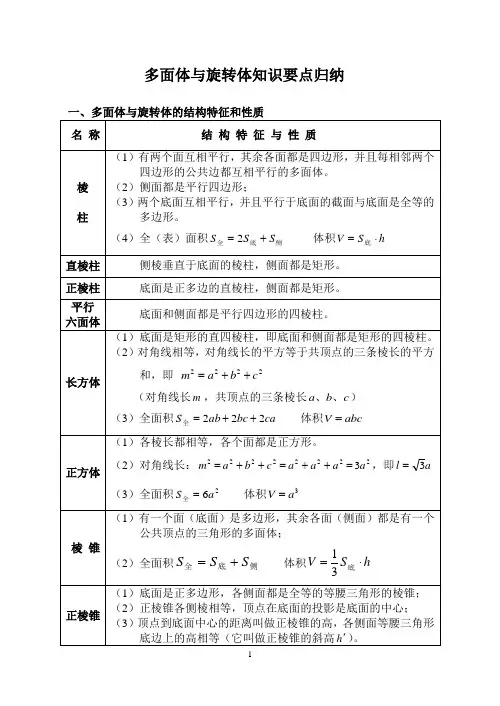
多面体与旋转体知识要点归纳
二、空间几何体的三视图和直观图
1.中心投影:光由一点向外散射形成的投影,叫做中心投影。
中心投影的投影线交于一点。
2.平行投影:在一束平行光线照射下形成的投影,叫做平行投影。
投影线正对着投影面时,叫做正投影,否则叫做斜投影。
平行投影的投影线是平行的。
3.三视图
正视图:光线从几何体的前面向后面正投影,得到的投影图叫做几何体的正视图。
侧视图:光线从几何体的左面向右面正投影,得到的投影图叫做几何体的侧视图。
俯视图:光线从几何体的上面向下面正投影,得到的投影图叫做几何体的俯视图。
画法:长对正、高平齐、宽相等。
4.直观图(斜二测画法)
(1)画坐标轴:把已知图形中互相垂直的x轴和y轴,在直观图中画成
45(或
135)角的x'轴和y'轴,
(2)画底面:已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴和y'轴的线段。
已知图形中平行于x轴的线段,在直观图中保持长度不
变,平行于y轴的线段,长度为原来的一半。
(3)画侧棱:侧棱的长度与原来几何体的侧棱的长度一样。


多面体和旋转体是高中数学中的重要概念,它们在几何学中起着重要的作用。
本篇文章将介绍多面体和旋转体的基本概念、性质以及它们在实际生活中的应用。
一、多面体多面体是指由若干个平面多边形围合而成的三维几何体。
每个面都是一个平面多边形,并且相邻两个面的公共边是相交于一点的。
多面体分为凸多面体和凹多面体,如果一个多面体的任何一个面都在另一个面的外部,则这个多面体是凸多面体;否则,这个多面体是凹多面体。
1. 多面体的性质(1)多面体的顶点数V和面数F之间有如下关系:V = F + E - 3,其中E表示边数。
这个公式称为欧拉公式。
(2)多面体的棱数E和面数F之间有如下关系:E = 3F - E - F,这个公式称为欧拉-斯图姆定理。
(3)多面体的对角线数D和面数F之间有如下关系:D = 2F - 4,这个公式称为拉格朗日定理。
2. 多面体的应用(1)多面体在计算机图形学中有着广泛的应用,例如,计算机生成的三维图形通常都是由许多平面多边形构成的。
(2)多面体在机械制造中也有着重要的应用,例如,制造凸轮、齿轮等零件时需要使用凸多面体或凹多面体的概念。
二、旋转体旋转体是指由一条平面曲线绕着它所在的平面内的一条定直线旋转所生成的立体。
曲线称为旋转体的母线,定直线称为旋转体的轴。
1. 旋转体的性质(1)如果一个旋转体的底面是一个圆,则这个旋转体一定是圆柱或圆锥;如果这个圆的半径等于旋转体的底面半径,则这个旋转体是圆柱;否则,这个旋转体是圆锥。
(2)如果一个旋转体的底面是一个椭圆或其他平面曲线,则这个旋转体一定是圆台或球;如果这个椭圆或其他平面曲线是旋转体的底面半径的倍数,则这个旋转体是圆台;否则,这个旋转体是球。
2. 旋转体的应用(1)旋转体在建筑工程中有着广泛的应用,例如,圆柱形和球形建筑物的外壳是由旋转体的概念构成的。
(2)旋转体在油管和通风管道的设计中也有着重要的应用。



第二章多面体和旋转体一多面体§2.1 棱柱一、素质教育目标(一)知识教学点1、棱柱的概念及性质。
2、平等六面体,长方体的概念及长方体的性质。
3、直棱柱直观图的画法4、棱柱侧面积的计算(二)能力训练点1、在学习棱住概念和性质过程中,努力提高学生的观察、抽象和概括能力。
2、通过直棱柱直观图的画法的教学,进一步提高学生的作图和识图能力。
3、通过直棱柱侧面积公式的教学,进一步增强学生把空间形转化为平面图形的意识,使学生进一步掌握化归的数学思想和方法,以提高学生分析问题、解决问题的能力。
(三)德育渗透点1、棱柱概念的形成,是从特殊到一般、具体到抽象的过程;通过教学使学生初步认识辩证唯物主义认识论的观点。
2、通过四面体、平行六面体、直平行六面体、长方体、正方体之间相互关系的教学,使学生树立普遍联系的唯物主义观点。
3、通过运用侧面积公式计算生产实践中具体零件的面积,使学生懂得数学对工、农业生产的意义,激励学生努力学好数学,将来为祖国的“四化”建设做出更大的贡献。
二、教学重点、难点、疑点及解决办法1、教学重点:理解棱柱的概念,掌握棱柱的性质及直棱柱侧面积公式,能利用性质及侧面积公式解决有关问题。
2、教学难点:直棱柱直观图的画法3、教学疑点:直棱柱的判断,注意引导学生严格按定义三、课时安排本课题建议安排3课时四、教与学过程设计第一课时节棱柱的概念及性质(一)引入将画有图2-1、图2-2、图2-3的小黑板挂出师:今天这一节课我们学习棱柱的概念和性质(给出课题),以上三个图形所表示的模型均为棱柱,下面我们一起来研究它们的共同特点。
(二)棱柱及有关概念的定义师:大家注意到图2-1到图2-3所表示的几何本均由一些面围成,而面与面之间有交线,因此可以从“面”和“线”两个角度去找它们的特点,先观察图2-1。
(1)首先看面:从面和面的关系及面的开头引导学生讨论,得出结论;有两个面互相平行,其余各面为四边形。
(2)再看线:从线与线之间的引导学生得出结论:每相邻两个四边形的公共边都互相平行。
![多面体与旋转体[优质ppt]](https://uimg.taocdn.com/a2db845727284b73f3425018.webp)
第七讲 多面体与旋转体多面体与旋转体是高中数学的重要内容之一,是考查各种能力的重要载体,其中异直线所成的角、直线与平面所成的角、二面角(理)以及点到平面的距离、简单图形侧面积与体积的计算是高考考查的重点内容。
本讲从内容上来说,主要集中在多面体与旋转体的概念与性质及其应用、截面面积、侧面积、全面积以及各种角与距离的计算等方面;从思想方法上来说,体会化“曲”为“直”、祖恒原理和图形割补等化归思想。
【高考热点】异面直线所成的角、直线与平面所成的角、二面角,空间线面位置关系的判断,面积与体积的计算。
【范例精讲】 例1.(1)正三棱锥S A B C -的侧棱,,SA SB SC 两两垂直,体积为V ,,,A B C '''分别是,,SA SB SC 上的点,且SC C S SB B S SA A S 41,31,21='='=',则三棱锥S A B C '''-的体积为( )(A )V 91(B )V121(C )V241(D )V721(2)如图,在多面体ABC D EF 中,已知A B C D 是边长为1的正方形,且A D EBC F ∆∆、均为正三角形,//,2EF AB EF =,则该多面体的体积为( ) (A 3(B 3(C )43(D )32解:(1)选C ;(2)选A 。
说明:对于第(1)小题,注意转化三棱锥的顶点灵活使用体积计算公式;对于(2)则需要利用图形的割补思想求解。
例2.在北纬45圈上有,A B 两点,设该纬度圈上,A B两点的劣弧长为4R (R 为地球半径),求,A B 两点间的球面距离。
解:设北纬45圈的半径为r ,则4r R =,设O '为北纬45圈的圆心,A O B α'∠=,则4r R α=,24R R α=,2πα=,所以AB R ==,在AB C ∆中,3A OB π∠=,所以,,A B 两点的球面距离等于3R π。
说明:要求两点的球面距离,应先由已知条件求出两点的直线距离,再求出这两点的球心角,进一步求出这两点的球面距离。
例3.图1是某储蓄罐的平面展开图,其中G C D ∠E D C =∠90F =∠=︒,且AD C D D E C G ===,FG FE =.若将五边形C D E F G 看成底面,AD 为高,则该储蓄罐是一个直五棱柱。
(1) 图2为面ABC D 的直观图,请以此为底面将该储蓄罐的直观图画完整;(2) 已知该储蓄罐的容积为31250cm V =,求制作该储蓄罐所需材料的总面积S (精确到整数位,材料厚度、接缝及投币口的面积忽略不计)。
解:(1) 该储蓄罐的直观图如右图所示;(2) 若设A D a =,则五边形C D E F G 的面积为254a ,得容积3512504V a ==,解得10a =,其展开图的面积2221550(116912S a a =++=+≈,因此制作该储蓄罐所需材料的总面积约为6912cm 。
例4.如图,在正四棱柱1111D C B A ABCD -中,4=AB ,81=AA 。
(1)求异面直线C B 1与11C A 所成角的大小;(用反三角函数形式表示)(2)若E 是线段1DD 上(不包含线段的两端点)的一个动.点.,请提出一个与三棱锥体积有关的数学问题(注:三棱锥需以点E 和已知正四棱柱八个顶点中的三个为顶点构成);并解答所提出的问题。
解:(1)如图,连接A C 、1A B ,由11//AA CC =,11D AB C DFGE图1ABCD图2AB CDFGE知11A ACC 是平行四边形,则11//A C AC =, 所以1B C A ∠为异面直线C B 1与11C A 所成角。
在1B C A ∆中,AC =11AB B C ==,则2221111cos 210AC B C AB AC B AC B C+-∠==⋅所以1arccos 10AC B ∠=(也可用向量求解)(2)第一种:提出问题:证明三棱锥1E B BC -的体积为定值。
问题解答:如图,因为1//D D 平面11B BCC ,所以1D D 上任意一点到平面11B BCC 的距离相等,因此三棱锥1E B BC -与三棱锥1D B B C -同底等高,11E B BC D B BC V V --=。
而11111644843323D B B C B B C V S D C -∆=⋅⋅=⨯⨯⨯⨯=,所以三棱锥1E B BC -的体积为定值643。
说明:若在侧面11B BCC 上任取三个顶点,与点E 构成三棱锥时,结论类似。
第二种:提出问题:三棱锥E A D C -的体积在E 点从点D 运动到1D 过程中单调递增。
问题解答:因为13E A D C A D C V S D E -∆=⋅⋅,知A D CS ∆为定值,则三棱锥E A D C -的体积与D E 成正比,可知E AD C V -随着D E 增大而增大,又因为()0,8DE ∈, 即三棱锥E A D C -的体积在E 点从点D 运动到1D 过程中单调递增。
说明:(1)若提出的问题是求三棱锥E A D C -的体积范围,也可。
11A1D1C 1A1D解答:因为8AD C S ∆=,而83E A D C V D E -=,()0,8DE ∈, 则64(0,)3E AD C V -∈。
(2)若在底面A B C D 上任取三个顶点,与点E 构成三棱锥时,结论类似;若在底面1111A B C D 上任取三个顶点,与点E 构成三棱锥时,结论类似(单调递减)。
【巩固提高】 一、填空题:1.正三棱锥的底面边长为6,侧棱长为,侧其体积为___________________。
2.在长方体1111ABC D A B C D -中,4A B B C ==,15AA =,P 是11C D 的中点,则直线P A 与平面A B C D 所成角的大小是___________________(结果用反三角函数值表示)。
3.已知正三棱柱的底面正三角形边长为2,侧棱长为3,则它的体积=V 。
4.圆锥的顶角为120°,高为a ,用过顶点的截面去截圆锥,则截面的最大面积为___。
5.棱长为a 的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为_____。
6.北纬45 圈上有,A B 两地,A 在东径120 ,B 在西径150 ,设地球半径为R ,,A B 两地球面距离为 ;7.若四棱锥P —ABCD 的底面是边长为a 的正方形,侧棱PA=a ,PB=PD=a 2,则在它的五个面中,互相垂直的面共有______对。
8.某厂生产的产品外形为正方体,棱长为cm 1,现设计一种长方体形纸箱做为包装,要求每个长方体形纸箱恰好装12件正方体形产品,则长方体形纸箱的表面积的值是_______2cm (只需写出一个可能的值)。
二、选择题:9.在正方体ABCD -A 1B 1C 1D 1中,下面结论错误..的是( ) (A ) BD ∥平面CB 1D 1 (B )AC 1⊥BD(C )AC 1⊥平面CB 1D 1 (D )异面直线AD 与CB 1角为6010.把边长为4和2的一个矩形绕其一边卷成一个圆柱的侧面,则圆柱的体积为( ) (A )16π(B )8π (C )16π或8π(D )16π或32π11.正四棱柱1111-ABC D A B C D 中,13,4AB BB ==,长为1的线段PQ 在棱1A A 上移动,长为3的线段M N 在棱1C C 上移动,点R 在棱1B B 上移动,则四棱锥R PQMN -的体积为( )(A )6 (B )10(C )12 (D )不确定12.在直三棱柱111-C B A ABC 中,2π=BAC ∠;1AA AC AB ===1.已知E G 与分别为11B A 和1CC 的中点,D 与F 分别为线段AC 和AB 上的动点(不包括端点).若EF GD ⊥,则线段DF 的长度的取值范围为 ( )(A)),155[(B ))2151[, (C )),21( (D )),2251(三、解答题:13.已知过球面上,,A B C 三点的截面和球心的距离为球半径的一半,且2AB BC C A ===,求球的表面积和体积。
14.在棱长为2的正方体1111D C B A ABCD -中,E 是棱11D C 的中点,F 是侧面D D AA 11的中心。
(1) 求三棱锥EF D A 11-的体积;(2) 求EF 与底面1111D C B A 所成的角的大小。
(结果用反三角函数表示)15.如图,直三棱柱111ABC A B C -底面A B C ∆中,1,CA CB ==90BCA ∠= ,棱12AA =,,M N 分别是111A B A A 、的中点(1)求B N 的长; (2)求BN 与CB 1所成的角;(3)求证:11C M A B ⊥。
16.如图,正方形A C D E 的边A E 与平面ABC 垂直,M 是C E 和A D 的交点,A C B C ⊥,且A C B C =。
(I )求证:A M ⊥平面EBC ;(II )求直线A B 与平面EBC 所成的角的大小; (III )求二面角A E B C --的大小。
参考答案:1.18 2.arctan23.33 4.22a 5.63a6.3R π7.4对8.50,40,38,32(只需写出一个可能的值) 9.D 10.D 11.C 12.A13.解:设截面圆心为O ',连结O A ',设球半径为R ,则22323O A '=⨯⨯=,在Rt O O A '∆中,222OA O A O O ''=+,所以222134R R =+,43R =,所以26449S R ππ==,3344425633381V R πππ⎛⎫==⋅= ⎪⎝⎭球。
14.解:(1)3111311111=⋅⋅==--F D A E EF D A V V 。
(2)取11D A 的中点G ,所求的角的大小等于GEF ∠的大小,在GEF Rt ∆中22tan =∠GEF ,所以EF 与底面1111D C B A 所成的角的大小是22arctan。
(也可用向量法求之)15.解:解法一:(1)因为点N 为直三棱柱侧棱中点所以N A A B ⊥,且1112AN AA ==, 又901BCA CB CA ∠===,,所以AB =所以||BN ==。
(2)分别延长111AA BB C C 、、至222A B C 、、,使222132A A B B C C A A ===,连结12B A ,则12//B A BN ,B N 与C B 所成的角,即为12B A 与C B 的夹角,连结2A C ,在21A B C ∆中,12B A BN ==1C B =2CA =12cos CB A ∠==所以异面直线BN 与CB 1所成的角为。