define_grid_motion的使用形式

FLUENT动网格需要的常用宏虽然瞬态PROFILE文件可以在一定程度上定义网格运动，然而其存在着一些缺陷。

最主要的一些缺陷存在于以下一些方面：（1）PROFILE无法精确的定义连续的运动。

其使用离散的点值进行插值。

如果想获得较为精确的运动定义，势必要定义很多点。

（2）一些情况下无法使用profile。

比如稳态动网格。

在FLUENT中定义网格运动，更多的是采用UDF宏。

fluent中与动网格有关的UDF 宏一共有5个，其中四个用于常规的网格运动定义，一个用于6DOF模型。

这些宏分别为：DEFINE_CG_MOTION、DEFINE_DYNAMIC_ZONE_PROPERTY、DEFINE_GEOM、DEFINE_GRID_MOTION、DEFINE_SDOF_PROPERTIES注意：动网格宏只能为编译型UDF。

1、DEFINE_CG_MOTION最常用的运动网格宏。

用户可以使用该宏定义每一时间步上的线速度或角速度来指定fluent中某一特定区域的运动。

DEFINE_CG_MOTION(name,de,vel,omega,time,dtime)参数说明：name：UDF的名字。

体现在fluent中表现为可选择的函数列表。

Dynamic_Thread *dt：存储了用户所指定的动网格属性和结构指针。

real vel[]：线速度。

vel[0]为x方向速度，vel[1]为y方向速度，vel[2]为z 方向速度real omega[]：角速度。

与线速度定义相同。

real time：当前时间。

real dtime：时间步长。

函数返回值为：void从函数的参数类型，配合c语言的参数调用方式可知，vel,omega为数值类型，属于传入类型。

因此只需在函数体中显式定义vel与omega即可将速度传入fluent求解器。

time与dtime是用于定义速度的。

详细实例可参看fluent udf 文档p182。

2、DEFINE_DYNAMIC_ZONE_PROPERTY该宏能用于以下一些场合：（1）在in-cylinder应用中定义旋转中心。

以NACA0012翼型俯仰振荡实例进行讲解动网格的应用过程；首先需要声明的是，这个例子也是来源于网络，原作者不详，在此向他表示感谢。

1、问题描述本例是想对作简谐振荡运动的NACA0012翼型的气动特性（升力系数，阻力系数和力矩系数）进行数值计算，来流速度为V，攻角的变化规律为：Alpha（t）=A/2*sin(omega*t)其中，A=10度，omega=10*pi 弧度/秒。

2、该例需要使用动网格来实现，首先需要编写刚体运动UDF实现翼型的俯仰运动，由于在FLUENT的UDF中只能指定速度，角速度；所以，需要将攻角对时间求导，得到转动角速度的规律：D（alpha）/dt=A*omega/2*cos(omega*t)编写的UDF在附件中。

3、由于本例只是为了讲述动网格的实现，至于其他方面的设置及分析就不再讨论；这里详细讲述下动网格的建立以及动网格的预览的结果。

步骤如下：1）将mesh文件读入到FLUENT中，Grid：check，scale…，Smooth/Swap…；Display Grid；2）定义求解器为，Define：pressure-based，2D，unsteady，Implicit，Green-Gauss Node Based（因本例使用的是三角形单元）.3）编译UDF，Define->User-Defined->Functions->Complied…此时打开了Complied UDFs的窗口，Add…在选择UDF的对话框中找到NACA0012DM文件夹中的airfoil.c文件，选中，ok；此时返回到Complied UDFs的窗口点击Build，FLUENT开始进行编译，可以在FLUENT窗口看到编译的一些过程提示；等编译完成，点击Load；就将已经编译好的UDF加载到FLUENT中了。

4）定义动网格参数，Define->Dynamic Mesh（选勾，激活动网格模型）->Parameters…此时打开了Dynamic Mesh Parameters 窗口，在Models中只选取Dynamic Mesh，本例的网格类型为三角形单元，要实现的运动为小幅度的转动，因此选用的动网格更新方法为Smoothing+Remeshing；开始依次对这两种更新方法进行参数设定：Smoothing中的参数设定：Spring Constant Factor（弹簧倔强系数），该值设定为一个较小的值，在0.01到0.1之间，本例选取0.08；Boundary Node Relaxation（边界节点松弛），设定为0.5；Convergence Tolerance（收敛判据），保持默认的0.001；Number of Iterations（迭代次数），保持默认的20；Remeshing中的参数设定：为了得到较好的网格更新，本例在使用局部网格重新划分方法时，使用尺寸函数，也就是Remeshing+Must Improve Skewness+Size Function的策略。

振动流化床仿真操作过程及参数选择1创建流化床模型。

根据靳海波论文提供的试验机参数，创建流化床模型。

流化床直148mm，高1m，开孔率9%，孔径2mm。

在筛板上铺两层帆布保证气流均布。

因为实验机为一个圆形的流化床，所以可简化为仅二维模型。

而实际实验中流化高度远小于1m，甚至500mm，所以为提高计算时间，可将模型高度缩为500mm。

由于筛板上铺设两层帆布以达到气流均分的目的，所以认为沿整个筛板的进口风速为均匀的。

最终简化模型如下图所示：上图为流化后的流化床模型，可以看出流化床下端的网格相对上端较密，因为流化行为主要发生的流化床下端，为了加快计算时间，所以采用这种下密上疏的划分方式。

其中进口设置为velocity inlet；出口设置为outflow；左右两边分为设置为wall。

在GAMBIT中设置完毕后，输出二维模型vfb.msh。

outflow边界条件不需要给定任何入口的物理条件，但是应用也会有限制，大致为以下四点：1.只能用于不可压缩流动2.出口处流动充分发展3.不能与任何压力边界条件搭配使用（压力入口、压力出口）4.不能用于计算流量分配问题（比如有多个出口的问题）2打开FLUENT 6.3.26，导入模型vfb.msh点击GRID—CHECK，检查网格信息及模型中设置的信息，核对是否正确，尤其查看是否出现负体积和负面积，如出现马上修改。

核对完毕后，点击GRID-SCALE 弹出SCALE GRID窗口，设置单位为mm，并点击change length unit按钮。

具体设置如下：3设置求解器保持其他设置为默认，更改TIME为unsteady，因为实际流化的过程是随时间变化的。

（1）pressure based 求解方法在求解不可压流体时，如果我们联立求解从动量方程和连续性方程离散得到的代数方程组，可以直接得到各速度分量及相应的压力值，但是要占用大量的计算内存，这一方法已可以在Fluent6.3中实现，所需内存为分离算法的1.5-2倍。

Fluent使用指南2第一步：网格1、读入网格（File→Read→Case）2、检查网格（Grid→Check）3、平滑网格（Grid→Smooth/Swap）4、更改网格的长度单位（Grid→Scale）5、显示网格（Display→Grid）第二步：建立求解模型1、保持求解器的默认设置不变（定常）2、开启标准K-ε湍流模型和标准壁面函数Define→Models→Viscous第三步：设置流体的物理属性ari→Density→viscosity→第四步：设置边界条件对outflow、velocity-inlet、wall 采用默认值第五步：求解1、Solv→Controls→Solution中，Discretitation→Pressure→standardPressure→Momentum→2、Solution Initialization→all zone3、Residual Monitors→Plot第六步:迭代第七步：进行后处理第八步：1、Define→Model→Evlerian2、在Vissous Model→K-epsilon Multiphase Model→Mixture 第九步：在Define Phase Model→Discrete phase ModelInteraction↓选中→Interaction With Continuous Phase Nomber of Continuous PhaseInteractions per DPM Interaction第十步：设置物理属性第十一步：Define→Operating →重力加速度Define→Boondary Conditionsflvid→Mixture→选中Sovrce Terms 其他默认Phase-1→选中Sovrce Terms 其他默认Phase-2→选中Sovrce Terms 其他默认inflow→Mixture→全部默认Phase-1→全部默认Phase-2→Multiphase→Volume Fraction→其他默认outflow→Mixture→默认Phase-1→默认Phase-2→默认wall→Mixture→全部默认Phase-1→默认Phase-2默认第十二步：Slove→Controls→Slution Controls→Pressure→Momentum→其余默认第十三步：千万不能再使用初始化第十四步：进行迭代计算截Z轴上的图:在Surface→iso↓Surface of constant↓Grid↓然后选x、y、z轴（根据具体情况而定）↓在Iso-Values→选取位置C的设置在New Surface Name中输入新各字→点创建然后在Display→Grid→Edge type→Feature→选中刚创建的那个面，然后Display查看刚才那面是否创建对最后在Display→Contours→Options→Filled→Surface→选中面，然后Display。

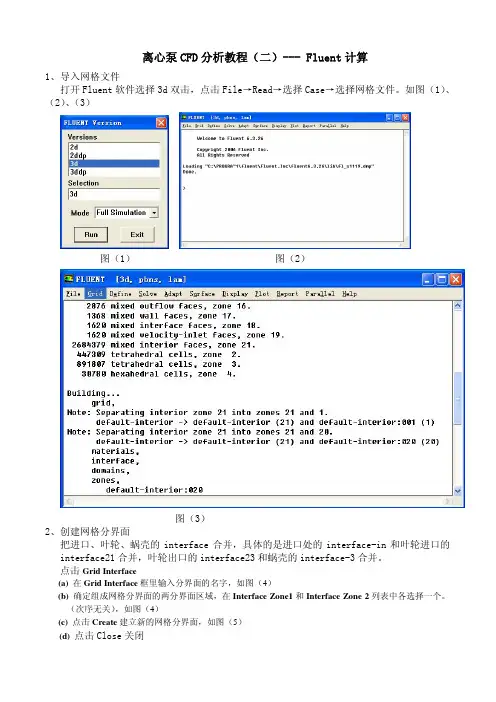
离心泵CFD分析教程（二）--- Fluent计算1、导入网格文件打开Fluent软件选择3d双击，点击File→Read→选择Case→选择网格文件。

如图（1）、（2）、（3）图（1） 图（2）图（3）2、创建网格分界面把进口、叶轮、蜗壳的interface合并，具体的是进口处的interface-in和叶轮进口的interface21合并，叶轮出口的interface23和蜗壳的interface-3合并。

点击Grid Interface(a) 在Grid Interface框里输入分界面的名字，如图（4）(b) 确定组成网格分界面的两分界面区域，在Interface Zone1和Interface Zone 2列表中各选择一个。

（次序无关），如图（4）(c) 点击Create建立新的网格分界面，如图（5）(d) 点击Close关闭图（4）图（5）注：1）创建网格分界面要在check网格之前，否则check网格时就会出错。

2）在创建网格分界面之后你会发现在Boundary Conditions里面多了四个边界（wall-13、wall-25、wall-27、wall-28），如图（6）图（6）3、check网格点击Grid → check，要留意如图（7）所示的volume statistics三项数据是否为正数，若为负数的话就要重新划分网格。

图（7）4、单位换算（scale Grid）点击Grid → scale Grid，在选择㎜，点击→，如图（8）图（8）5、平滑、交换网格点击Grid → Smooth/Swap Grid 如图（9）图（9）点击→，如图(10)，继续→直到多次为零而止,如图(11)图（10） 图 (11)注：这对于非结构网格来说非常重要。

6、求解器设置点击Define→Modles→Solver,在Time下面选择steady(定常)，点击OK，如图（12） 一般离心泵可选择定常，如果要测算瞬态流的话就要选择Unsteady图（12）7、湍流模型选择点击Define→Modles→Viscous Modle,选择k-epsilon(2kqn), 点击OK，如图（13）图（13）8、设置流体物性点击Define→Materials→右侧Fluent Database(如图14)→在Fluent Fluid Materials 里面选择Water-liquid(H2o<l>)（如图15）,点击Copy→Close图（14）.9、设置旋转单位点击Define→Units→angular-velocity→rpm→Close，如图（16）如图（16）10、设置运行条件点击Define→Operating Conditions→点击Gravity(重力)前面的小方块，在重力的作用坐标线上填上大小，负号表示重力的方向和坐标方向相反→点击OK在Operating Pressure可以设置参考压力，一般默认为一个大气压。

define_grid_motion的使用形式-回复问题：define_grid_motion的使用形式define_grid_motion是一个功能强大的工具，用于定义和控制网格动画的移动。

它通常用于Web开发中，通过对元素的位置和动画进行精细控制，实现更流畅和吸引人的用户体验。

本文将详细介绍define_grid_motion的使用形式，并提供一步一步的指导。

第一步：安装和导入define_grid_motion库首先，确保你的项目已经安装了define_grid_motion库。

你可以通过在终端中运行以下命令来安装它：npm install define_grid_motion或者，你可以在HTML文件中使用script标签直接导入库的最新版本：html<script src="一旦库安装完毕，你就可以在你的代码中导入它。

javascriptimport { defineGridMotion } from 'define_grid_motion';第二步：创建一个容器元素来进行动画在HTML文件中，你需要创建一个用于显示动画的容器元素。

你可以使用任何HTML元素来作为容器，比如一个div元素。

html<div id="animation-container"></div>第三步：定义和配置网格动画在你的JavaScript代码中，你需要定义和配置网格动画。

首先，获取容器元素的引用：javascriptconst animationContainer =document.getElementById('animation-container');接下来，创建一个网格动画实例，并将它附加到容器上：javascriptconst gridMotion = new defineGridMotion(animationContainer);现在你可以开始定义和配置动画了。

vueuse motion使用Vueuse Motion是一个Vue3的动画库，基于Motion和Framer Motion。

它提供了一组用于创建、控制和组合动画效果的组件和指令。

使用Vueuse Motion，首先需要安装它：```bashnpm install vueuse/motion@next```然后在Vue应用程序的入口文件中引入和使用它：```javascriptimport { createApp } from 'vue'import { motionPlugin } from '@vueuse/motion'import App from './App.vue'const app = createApp(App)e(motionPlugin)app.mount('#app')```接下来，就可以在应用程序中使用动画效果了。

比如，可以使用`<m-motion>`组件来创建动画效果：```vue<template><m-motion :initial="false" :opacity="0" :x="100"><div>Hello Vueuse Motion!</div></m-motion></template>```这里的`<m-motion>`组件接受多个属性，比如`initial`表示初始状态是显示还是隐藏，`opacity`表示透明度，`x`表示水平方向的偏移量等等。

除了使用`<m-motion>`组件，还可以使用`v-motion`指令来为任意元素添加动画效果：```vue<template><div v-motion:fade="'in'">Hello Vueuse Motion!</div></template>```这样，元素就会在页面中淡入淡出。

define grid motion相对坐标系Grid motion is a concept that is commonly used in the field of robotics and computer vision. It refers to the motion of objects or points in a 2D or 3D space relative to a grid-based coordinate system. In this article, we will explore the concept of grid motion in the context of a relative coordinate system in detail, discussing its applications, advantages, and limitations.To begin with, let's understand the basic idea of a grid-based coordinate system. In a grid-based coordinate system, a 2D or 3D space is divided into a set of equally spaced grid cells. Each grid cell is identified by its unique coordinates, usually represented by a combination of integers. For example, in a 2D grid, a point can be denoted by (x, y), where x represents the horizontal axis and y represents the vertical axis.In the context of grid motion, we consider the relative motion of an object or point with respect to this grid-based coordinate system. It means that the motion is measured and described in terms of changes in the object or point's coordinates relative to the grid.Now, let's dive deeper into the applications of grid motion in thefield of robotics and computer vision. One prominent application lies in the area of mapping and localization. By tracking the movements of an object or a robot in a grid-based coordinate system, we can build a map of the environment and accurately determine the position of the object or robot within that map. This is particularly useful in scenarios such as autonomous driving, where precise localization is essential for safe and efficient navigation.Another application of grid motion is in object tracking and motion estimation. By analyzing the relative changes in the grid coordinates of an object or point, we can estimate its velocity, acceleration, and trajectory. This information can be utilized to predict the future motion of the object or to detect abnormal movements, thus enabling various applications in surveillance, sports analysis, and virtual reality.Now, let's discuss the advantages of using grid motion in a relative coordinate system. One significant advantage is its simplicity and intuitive understanding. Grid-based coordinate systems are easy to visualize and comprehend, making it easier for humans to interpret and analyze the motion of objects or points. This simplicity alsofacilitates the implementation of algorithms and techniques for motion analysis, as the calculations can be performed based on the changes in grid coordinates directly.Furthermore, grid motion provides a discrete representation of motion, which can be advantageous in many scenarios. By discretizing the motion into a grid, we can effectively reduce the complexity of the problem and simplify the calculations. This is particularly beneficial when dealing with large-scale environments or when real-time performance is required.However, it is important to acknowledge the limitations of grid motion in a relative coordinate system. One limitation is its sensitivity to the grid resolution. The accuracy and precision of the motion estimation depend on the size of the grid cells. Smaller grid cells enable finer-grained motion analysis but may require more computational resources. On the other hand, larger grid cells may lead to higher quantization errors and less accurate motion estimation.Additionally, grid motion assumes that the motion is constrained within the grid cells. In reality, objects or points may move in acontinuous space, which can result in errors when estimating their motion based on the discrete grid coordinates. Therefore, it is crucial to consider the assumptions and limitations of grid motion when designing algorithms and systems based on this concept.In conclusion, grid motion in a relative coordinate system is a powerful concept used in robotics and computer vision for analyzing the motion of objects or points. By tracking their movements with respect to a grid-based coordinate system, we can accurately estimate their motion, predict future movements, and perform various tasks such as mapping, localization, and object tracking. While grid motion offers simplicity and intuitive understanding, it is essential to consider its limitations regarding grid resolution and the assumption of discrete motion.。