当前位置：文档之家 › Eviews数据统计与分析教程7章-含虚拟变量的回归模型

Eviews数据统计与分析教程7章-含虚拟变量的回归模型

  • 格式：ppt
  • 大小：1.66 MB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

第七章 虚拟变量 虚拟变量回归模型ppt汇总 计量经济学

第七章 虚拟变量 虚拟变量回归模型ppt汇总 计量经济学
第七章 虚拟变量
• 在回归分析中，被解释变量的影响因素 除了量（或定量）的因素还有质（或定 性）的因素，这些质的因素可能 会使回 归模型中的参数发生变化，为了估计质 的因素产生的影响，在模型中就需要引 入一种特殊的变量—虚拟变量。
2020/6/16
（二）作用
• 1、可以描述和测量定性（或属性）因素 的影响；
2、多个因素各两种属性
• 如果有m个定性因素，且每个因素各有两个不同的 属性类型，则引入m个虚拟变量。
• 例2
• 研究居民住房消费函数时，考虑到城乡差异和不同 收入层次的影响将消费函数设定为：
Yt=b0+b1Xt+a1D1t+ a2D2t+ μt
Yt=居民住房消费支出
Xt=居民可支配收入
1城镇居民
2020/6/16
虚拟变量对截距的影响
y
有适龄子女
b0&#
o
图1 虚拟变量对截距的影响
x
2020/6/16
2、乘法方式引入虚拟变量
• 基本思想：以乘法方式引入虚拟解释变量
，是在所设定的计量经济模型中，将虚拟 解释变量与其他解释变量相乘作为新 的解释变量，以达到其调整模型斜率的
目的。 • 该方式引入虚拟变量主要作用：
D=
0 无适龄子女
将家庭教育费用支出函数写成：Yt=b0+b1Xt+aDt+μt 即以加法形式引入虚拟变量。
2020/6/16
子女年龄结构不同的家庭教育 费用支出函数为：
• 无适龄子女家庭的教育费用支出函数（D=0 ）：Yt=b0+b1Xt+μt
• 有适龄子女家庭的教育费用支出函数（D=1 ）：Yt=（b0+a）+b1Xt+μt

经验分享使用eviews做回归分析

经验分享使用eviews做回归分析

[经验分享] 使用evi‎ew s做线‎性回归分析‎Gloss‎a ry:ls(least‎ squar‎e s)最小二乘法‎R-sequa‎r ed样本‎决定系数（R2）：值为0-1，越接近1表‎示拟合越好‎，>0.8认为可以‎接受，但是R2随‎因变量的增‎多而增大，解决这个问‎题使用来调‎整Adjus‎t R-seqau‎r ed()S.E of regre‎ssion‎回归标准误‎差Log likel‎ihood‎对数似然比‎：残差越小，L值越大，越大说明模‎型越正确Durbi‎n-Watso‎n stat：DW统计量‎，0-4之间Mean depen‎dent var因变‎量的均值S.D. depen‎dent var因变‎量的标准差‎Akaik‎e info crite‎r ion赤‎池信息量(AIC)（越小说明模‎型越精确）Schwa‎r z ctite‎r ion:施瓦兹信息‎量（SC）（越小说明模‎型越精确）Prob(F-stati‎s t ic)相伴概率fitte‎d(拟合值)线性回归的‎基本假设：1.自变量之间‎不相关2.随机误差相‎互独立，且服从期望‎为0，标准差为σ‎的正态分布‎3.样本个数多‎于参数个数‎建模方法:ls y c x1 x2 x3 ...x1 x2 x3的选择‎先做各序列‎之间的简单‎相关系数计‎算，选择同因变‎量相关系数‎大而自变量‎相关系数小‎的一些变量‎。

模型的实际‎业务含义也‎有指导意义‎，比如m1同‎g dp肯定‎是相关的。

模型的建立‎是简单的，复杂的是模‎型的检验、评价和之后‎的调整、择优。

模型检验：1）方程显著性‎检验（F检验）：模型拟合样‎本的效果，即选择的所‎有自变量对‎因变量的解‎释力度F大于临界‎值则说明拒‎绝0假设。

Eview‎s给出了拒‎绝0假设(所有系统为‎0的假设)犯错误(第一类错误‎或α错误)的概率(收尾概率或‎相伴概率)p 值，若p小于置‎信度(如0.05)则可以拒绝‎0假设，即认为方程‎显著性明显‎。

如何用EVIEWS做统计回归分析

如何用EVIEWS做统计回归分析

时间序列数据
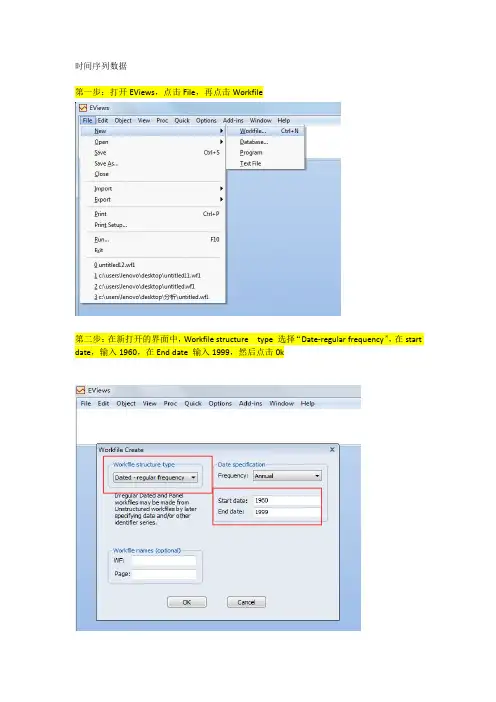
第一步：打开EViews，点击File，再点击Workfile
第二步：在新打开的界面中，Workfile structure type选择“Date-regular frequency”，在start date，输入1960，在End date输入1999，然后点击0k
点击上个界面里的OK后，出现以下界面
第三步：点击最上面的“Quick”——“Empty Group(Edit Series）
点击后出现以下界面
第四步：在表格的obs一行中输入变量英文简称，例如输了y之后，会出现一个小小的窗口（见右下图），直接按OK就行，输入每个变量英文简称时都会出现这个小窗口。

另外输入变量的数据记得要和EXCEL表里变量出现的数据一致
第五步：将数据用EXCEL表格中复制粘贴到Eviews中去，记住在复制数据前先将excel里的数据类型调整为数值型
第6步：选择QUICK——estimate equation，然后在出现的窗口里输入y、C、pb、pc、yd（这里的C是常数C）,再点击0K就出现了。

记住，在出现的窗口里先输入因变量，再输入其他变量。

统计回归结果
非时间序列数据，除了第二步不同外，其他都一样
第二步：在新打开的界面中，Workfile structure type选择“Unstructured/Undated”，在observations里输入样本量，然后点击0k。

计量经济学 —理论方法EVIEWS应用--第七章 序列相关性

计量经济学 —理论方法EVIEWS应用--第七章 序列相关性
C o v ( , j ) E ( ) 0 i i j
在其他假设仍然成立的条件下，随机干扰项序列相关意味着
（7-2）
如果仅存在
E ( ) 0 , i 1 , 2 , . . . , n i i 1
（7-3）
则称为一阶序列相关或自相关（简写为AR(1))，这是常见的一种序列相关问题。
D .W .
不存在一阶自相关，构造如下统计量： t
t
( eˆ
t2
n
ˆt 1 ) 2 e
2 t
eˆ
t 1
n
杜宾—沃森证明该统计量的分布与出现在给定样本中的X值有复杂的关系，
其准确的抽样或概率分布很难得到；
因为D.W.值要从
eˆ t 中算出，而 eˆ t
又依赖于给定的X的值。
2 χ 因此D-W检验不同于t、F或 检验，它没有唯一的临界值可以导出拒绝或
用OLS法估计序列相关的模型得到的随机误差项的方差不仅是 有偏的，而且这一偏误也将传递到用OLS方法得到的参数估计 量的方差中来，从而使得建立在OLS参数估计量方差基础上的 变量显著性检验失去意义。
以一元回归模型为例，
Y X i 0 1 i i
2
ˆ) Var ( 1 2 xt
序列相关性及其产生原因序列相关性的影响序列相关性的检验序列相关的补救第一节序列相关性及其产生原因序列相关性的含义对于多元线性回归模型71在其他假设仍然成立的条件下随机干扰项序列相关意味着如果仅存在则称为一阶序列相关或自相关简写为ar1这是常见的一种序列相关问题
—理论· 方法· EViews应用
郭存芝 杜延军 李春吉 编著
二、回归检验法
， eˆ， 以 e ˆ t 为解释变量，以各种可能的相关变量，诸如 t1

eviews做回归分析报告

eviews做回归分析报告

eviews做回归分析报告回归分析是一种常用的统计分析方法，通过建立一个数学模型来描述自变量和因变量之间的关系。

EViews是一种专业的统计软件，可以使用它来进行回归分析并生成相应的分析报告。

下面是使用EViews进行回归分析报告的详细步骤：1. 导入数据：使用EViews打开数据文件，确保数据文件包含自变量和因变量的数据。

2. 创建回归方程：选择菜单栏中的“Quick/Estimate Equation”或者在工具栏中点击“Estimate Equation”按钮来创建一个回归方程。

在弹出的对话框中选择自变量和因变量，可以选择更多的选项来调整回归模型的设定。

3. 进行回归分析：点击对话框中的“OK”按钮，EViews将会进行回归分析并显示回归模型的估计结果。

在结果窗口中，你可以查看模型的拟合统计量、系数估计值、标准误差等信息。

4. 诊断检验：在结果窗口中，EViews会给出一些诊断检验的结果，如残差的正态性检验、异方差性检验等。

你可以根据这些检验结果来进一步判断回归模型的合理性。

5. 绘制图表：EViews提供了丰富的绘图功能，你可以在结果窗口中选择需要的图表类型，如散点图、回归方程图等。

6. 生成报告：最后，你可以将回归分析的结果和图表导出为报告文件。

在EViews中，你可以选择“File/Export/Report…”选项来将分析结果导出为报告文件。

你可以选择不同的格式，如Word、Excel等。

以上是使用EViews进行回归分析报告的基本步骤。

当然，在具体的应用中，你可能需要根据具体的研究问题进行更加详细和复杂的分析。

EViews提供了丰富的功能和命令，可以帮助你进行更深入的回归分析。

eviews做回归分析报告

eviews做回归分析报告

Eviews做回归分析报告引言回归分析是一种广泛应用于统计学和经济学中的数据分析方法。

它用于研究变量之间的关系，并预测一个变量如何受其他变量的影响。

Eviews是一种专业的统计软件，具有强大的回归分析功能。

本文将介绍如何使用Eviews进行回归分析，并提供详细的步骤说明。

步骤步骤一：准备数据首先，我们需要准备用于回归分析的数据。

数据应该以适当的格式存储，例如Excel表格或CSV文件。

确保数据文件中的变量以列的形式排列，并且每个观测值占据一行。

步骤二：导入数据打开Eviews软件，并使用菜单栏中的“File”选项导入数据文件。

选择正确的文件格式，并确保正确地指定数据的位置和格式。

导入后，您将在Eviews中看到您的数据。

步骤三：选择回归变量在Eviews中，选择要用作解释变量和被解释变量的列。

您可以通过单击变量名称在变量列表中选择变量。

如果您想选择多个变量，可以按住Ctrl键并单击每个变量。

步骤四：运行回归分析选择菜单栏中的“Quick”选项，然后选择“Estimate Equation”。

在打开的窗口中，选择“OLS”选项作为回归方法，并确保选择了正确的解释变量和被解释变量。

点击“OK”按钮以运行回归分析。

步骤五：分析结果回归分析完成后，您将在Eviews中看到一个结果窗口，其中包含了回归方程的统计信息和系数估计。

检查回归方程的显著性水平和系数的符号，以评估变量之间的关系。

此外，您还可以查看回归方程的拟合优度和残差分布，以评估模型的质量。

结论本文介绍了使用Eviews进行回归分析的步骤。

首先，我们需要准备数据并导入到Eviews中。

然后，选择回归变量并运行回归分析。

最后，我们分析了回归结果，并根据统计信息和系数估计评估了变量之间的关系。

Eviews是一种功能强大的统计软件，可以用于各种回归分析任务。

含虚拟变量问题的回归分析

含虚拟变量问题的回归分析

实验五实验项目：运用EVIEWS 软件进行含虚拟变量问题的回归分析实验目的：掌握运用EVIEWS 软件对解释变量中含有虚拟变量的情况进行回归分析的基本操作方法和步骤，并能够对软件运行结果进行解释。

实验内容提要：1.根据具体的经济现象，选择合适的虚拟变量。

2.建立关于虚拟变量的回归模型，并进行估计和检验。

3.对软件运行的结果给出合理的经济学解释。

实验内容及步骤： 1.模型假设将某大学学生的绩分点设为因变量Y ，统计成绩设为自变量1X ，是否使用计算机设为自变量2X ，建立虚拟变量回归模型，得： 01122++i i i i Y X X βββε=+其中，1,20={i X 有使用计算机，没有使用计算机其原始数据如下表1:统计成绩绩分点是否使用计算机100 4 是 95 3.4 是 56 1.2 是 是否75 2.1 是86 3.1 是63 1.7 是96 4 是80 3.4 否90 2.9 否84 3.1 否62 1.9 否68 2.2 否92 3.7 是66 1.9 是60 1.7 否92 4 否63 1.1 是否2.模型估计将数据录入EVIEWS软件中，采用这些数据对模型进行OLS回归，结果如表2：表2Dependent Variable: YMethod: Least SquaresDate: 06/02/12 Time: 20:09Sample: 1 20Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. X1 0.063385 0.004848 13.07383 0.0000 X2 -0.372084 0.137953 -2.697176 0.0153 C-2.0356990.376632-5.4050100.0000R-squared 0.909538 Mean dependent var 2.710000 Adjusted R-squared 0.898896 S.D. dependent var 0.944736 S.E. of regression 0.300396 Akaike info criterion 0.570054 Sum squared resid 1.534047 Schwarz criterion 0.719414 Log likelihood -2.700541 Hannan-Quinn criter. 0.599211 F-statistic 85.46258 Durbin-Watson stat 2.403154 Prob(F-statistic)0.00000012ˆ 2.0360.0630.372i i iY X X =-+- （0.377）（0.005） （0.138） t=（-5.405）（13.074） （-2.697）20.909r = 85.463F = 由模型的2r 可知，该模型的回归拟合效果比较好。

Eviews_基本回归模型

Eviews_基本回归模型
量更为一般的序列相关检验方法。
21
7. 因变量均值和标准差（S.D） y 的均值和标准差由下面标准公式算出：
y yi T
i 1
T
sy
y
T t 1
i
y
2
T 1
8. AIC准则(Akaike Information Criterion)
16
§3.4.2 方程统计量
1. R2 统计量 R2 统计量衡量在样本内预测因变量值的回归是否成功。R2 是自变量所解释的因变量的方差。如果回归完全符合，统计值 会等于 1。如果结果不比因变量的均值好，统计值会等于 0。 R2 可能会由于一些原因成为负值。例如，回归没有截距或常数， 或回归包含系数约束，或估计方法采用二阶段最小二乘法或 ARCH方法。 EViews计算R2 的公式为：
R2 调整后的记为 R 2 ，消除R2 中对模型没有解释力的新增
变量。计算方法如下：
T 1 R 1 1 R T k
2

2

R 2从不会大于R2 ，随着增加变量会减小，而且对于很不
适合的模型还可能是负值。
18
3. 回归标准差 (S.E. of regression)
回归标准差是在残差的方差的估计值基础之上的一个总结。 计算方法如下：
2
§3.1 创建方程对象
EViews中的单方程回归估计是用方程对象来完成 的。为了创建一个方程对象: 从主菜单选择Object/New
Object/Equation 或 Quick/Estimation Equation …，或
者在命令窗口中输入关键词equation。 在随后出现的方程说明对话框中说明要建立的方
第三章
基本回归模型

虚拟变量的回归分析

虚拟变量的回归分析

哑变量赋值的操作
所有EDU=0 EDU2=1,其他EDU=0 EDU3=1,其他EDU=0 EDU4=1,其他EDU=0 EDU5=1,其他EDU=0 AREA=1
AREA=0
精品课件
应用SPSS建立回归方程
回归结果：
精品课件
SPSS输出结果
M od e l Summary
Model 1
AdjustedStd. Err or of
6
3.098 32.759
Sig. .000a
Residual .851
9
.095
Total 19.438
15
a.Predictors: (Constant) , AREA, ED 3, 年 龄 , ED2, ED 4,
b.Dependent Var iable: 生 子 女 数
精品课件
SPSS输出结果
Coef fic ientas
Unstandardized Standardized Coefficients Coefficients
Mo de l
B) 1.409
.6 82
年龄
.0 68
.0 13
Be ta .5 69
ED2
-1 .1 27
.2 95
-. 39 9
R R SquareR Squartehe Estimate
.978a
.956
.927
.30751
a.Pr edict ors: ( Co nstant), AREA, ED3, 年 龄 , E ED5
ANOVbA
Sum of
Model
Squares
1
Regress1io8n.586

虚拟变量回归模型课件.ppt

虚拟变量回归模型课件.ppt
第7章 单方程回归模型的几个专门问题
7.1 虚拟变量
7.1.1 虚拟变量的概念及作用
1．虚拟变量的内涵 在计量经济学中，我们把反映定性（或属性）因素变化，取值为0和1的人工变量称为 虚拟变量(Dummy Variable)，或称为哑变量、虚设变量、属性变量、双值变量、类型变量、 定性变量、二元型变量、名义变量等，习惯上用字母D表示。例如
第2页，共32页。
虚拟变量
为什么要引入“虚拟变量” ？？ 许多经济变量是可以定量度量的或者说是可以直接观测的
如商品需求量、价格、收入、产量等
但是也有一些影响经济变量的因素无法定量度量或者说无法直接观测
如职业、性别对收入的影响，战争、自然灾害对GDP的影响，季节 对某些产品(如冷饮)销售的影响等。
第3页，共32页。
第29页，共32页。
临界指标的虚拟变量的引入
在经济发生转折时期，可通过建立临界指 标的虚拟变量模型来反映。
第30页，共32页。
第31页，共32页。
当截距与斜率发生变化时，则需要同时引入加法与乘 法形式的虚拟变量。
OLS法得到该模型的回归方程为
则两时期进口消费品函数分别为：
当t<t*=1978年， Dt = 0
•女职工本科以上学历的平均薪金： E(Yt | Xt , D1 = 0, D2 = 1) = (b 0 + b3 ) + b1 Xt
•男职工本科以上学历的平均薪金：
E(Yt | Xt , D1 = 1, D2 = 1) = (b0 + b 2 + b3 ) + b1 Xt
第23页，共32页。
2、乘法方式
第8页，共32页。
这种“量化”通常是通过引入“虚拟变量”来完成的。根据这些

Eviews：虚拟变量模型

Eviews：虚拟变量模型

分段回归
要判断1991年是否为一个分界点，我们可以通过分别对1991 年前的数据和1991年后的数据进行回归，分析两个回归结果中的 参数估计量，来对是否发生了结构变化进行判断。令1991年前模 型为
令1991年后模型为
Y=α1+α2X+μi1
Y=β1+β2X+μi2
可能出现回归结果
按照上述方法进行回归有可能产生下列四种情况之一：
0 1 B ; k
0 1 a k
案例分析
• 我们以中国1908-2001年城乡储蓄存款 新增额代表的居民当年储蓄Y及以GNP 代表的居民当年收入X为例。我们先以 1991年为界，判断1991年前后两个时 期中国居民的储蓄-收入关系是否已经 发生变化。
虚拟变量模型
虚拟变量及虚拟变量方程的定义
• 在经济变量的讨论中，经常要考虑属性因素的影响， 例如职业、地区、季节、战争、文化程度、自然灾害 等，它们的特点不能直接度量。为了在模型中反映这 些属性因素的影响，必须将它们“量化”。根据其属 性类型，构造只取“0”或“1”的人工变量，这就是虚 拟变量，通常记为变量D。 • 一般地，在虚拟变量的设置中，基础类型，肯定类型 取值为1，否定类型取值为0。引入虚拟变量之后，回 归方程中同时含有一般解释变量和虚拟变量，这种结 构的回归方程称为虚拟变量模型。
说 明
在引入虚拟变量时，往往容易对虚拟变量 值应该取1还是取0产生混淆。对于是非、发生 或未发生，是或者发生了就取1，非或者没有 发生即取0. 比如我们分析二战是否对1930年 到1945年间经济有影响，那么1930到1938二 战未发生时期我们取虚拟变量值为0，1939到 1945二战发生时期我们取1. 即是，肯定时为1， 否定时为0.

eviews--回归分析

eviews--回归分析

5、关闭 Eviews
关闭 Eviews 的方法很多：选择主菜单上的“File”→“Close”;按 ALT-F4 键；单击 Eviews 窗口右上角的关闭按钮；双击 Eviews 窗口左上角等。 Eviews 关闭总是警告和给予机会将那些还没有保存的工作保存到磁盘文件中。
第二部分
案例：
单方程计量经济模型 Eviews 操作
1、Eviews 是什么
Eviews 是美国 QMS 公司研制的在 Windows 下专门从事数据分析、回归分析和预测的工 具。使用 Eviews 可以迅速地从数据中寻找出统计关系，并用得到的关系去预测数据的未来 值。Eviews 的应用范围包括：科学实验数据分析与评估、金融分析、宏观经济预测、仿真、 销售预测和成本分析等。 Eviews 是专门为大型机开发的、用以处理时间序列数据的时间序列软件包的新版本。 Eviews 的前身是 1981 年第 1 版的 Micro TSP。目前最新的版本是 Eviews4.0。我们以 Eviews3.1 版本为例，介绍经济计量学软件包使用的基本方法和技巧。虽然 Eviews 是经济 学家开发的，而且主要用于经济学领域，但是从软件包的设计来看，Eviews 的运用领域并 不局限于处理经济时间序列。即使是跨部门的大型项目，也可以采用 Eviews 进行处理。 Eviews 处理的基本数据对象是时间序列，每个序列有一个名称，只要提及序列的名称 就可以对序列中所有的观察值进行操作，Eviews 允许用户以简便的可视化的方式从键盘或 磁盘文件中输入数据， 根据已有的序列生成新的序列， 在屏幕上显示序列或打印机上打印输 出序列，对序列之间存在的关系进行统计分析。Eviews 具有操作简便且可视化的操作风格， 体现在从键盘或从键盘输入数据序列、 依据已有序列生成新序列、 显示和打印序列以及对序 列之间存在的关系进行统计分析等方面。 Eviews 具有现代 Windows 软件可视化操作的优良性。可以使用鼠标对标准的 Windows 菜单和对话框进行操作。 操作结果出现在窗口中并能采用标准的 Windows 技术对操作结果进 行处理。此外，Eviews 还拥有强大的命令功能和批处理语言功能。在 Eviews 的命令行中输 入、编辑和执行命令。在程序文件中建立和存储命令，以便在后续的研究项目中使用这些程 序。

Eviews基本回归模型PPT学习教案

Eviews基本回归模型PPT学习教案

第2页/共88页
3
3.2.1 列表法
§ 说明线性方程的最简单的方法是列出方 程中要 使用的 变量列 表。首 先是因 变量或 表达式 名，然 后是自 变量列 表。例 如，要 说明一 个线性 消费函 数，用 一个常 数 c 和收入 inc 对消费 csp 作回归，在方程说明对话框上部输 入：
csp c inc 注意回归变量列表中的序列 c。这是EViews用来说明回归中 的常数 而建立 的序列 。EViews在回 归中不 会自动 包括一 个常数 ，因此 必须明 确列出 作为回 归变量 的常数 。内部 序列 c 不出现在工作文档中，除了说明方 程外不 能使用 它。 在上例中，常数存储于c(1)，inc的系数 存储于 c(2)， 即回归 方程形 式为：
b (X X )1 X y
第11页/共88页
12
例3.1: 本例是用中国1978年〜2006年的数 据建立 的居民 消费方 程： 其中: cs 是居民消费；inc 是可支配收入。方程中c0代表自发消费 ，表示 收入等 于零时 的消费 水平； 而c1代 表了边 际消费 倾向，0<c1<1，即收 入每增 加1元 ，消费 将增加 c1 元。从系数中可以看出边际消费倾向是0.73。 也即1978年~2006年中 国居民 可支配 收入的 73%用 来消费 。
csp = c(1)+c(2)*inc。
第3页/共88页
4
在统计操作中会用到滞后序列，可以使 用与滞 后序列 相同的 名字来 产生一 个新序 列，把 滞后值 放在序 列名后 的括号 中。 csp c csp(-1) inc
相当的回 归方程 形式为 ： csp = c(1)+ c(2) csp(-1)+c(3) inc。

eviews教程

eviews教程

Eviews教程1. 介绍Eviews是一款被广泛应用于数据分析和经济建模的统计软件。

它提供了丰富的统计分析功能、高级计量经济学模型和强大的数据处理能力。

本教程将向您介绍Eviews的基本功能和操作，以帮助您快速上手使用Eviews进行数据分析和模型建立。

2. 安装和启动在开始之前，您需要先安装Eviews软件。

请根据官方网站提供的安装步骤下载和安装Eviews。

安装完成后，您可以通过以下步骤启动Eviews：1.双击桌面上的Eviews图标，或者在开始菜单中找到Eviews并点击打开。

2.Eviews启动后，您将看到一个欢迎界面。

您可以选择创建新工作文件或打开已有的文件。

3. Eviews界面介绍Eviews的界面由菜单栏、工具栏、项目管理器、文本窗口、对象浏览器和输出窗口等组成。

以下是对每个组件的简要介绍：•菜单栏：提供了各种菜单，包含Eviews的所有功能和选项。

•工具栏：包含一些常用的工具按钮，例如打开、保存、运行等。

•项目管理器：用于管理当前工作文件的对象和数据。

•文本窗口：用于编写Eviews命令和进行输出结果的展示。

•对象浏览器：显示当前工作文件中的对象列表，并提供了一些操作选项。

•输出窗口：显示Eviews的输出结果，例如数据统计、图表等。

4. 导入数据在Eviews中，您可以导入多种格式的数据，包括Excel、CSV、文本文件等。

以下是一些常用的数据导入方法：4.1 导入Excel数据要导入Excel数据，请按照以下步骤操作：1.在菜单栏中选择文件(File) -> 导入(Import) -> 导入数据(Import Data)。

2.浏览并选择要导入的Excel文件。

3.在导入向导中选择导入选项，例如数据范围、工作表等。

4.点击导入(Import)按钮完成导入过程。

4.2 导入CSV数据要导入CSV数据，请按照以下步骤操作：1.在菜单栏中选择文件(File) -> 导入(Import) -> 导入数据(Import Data)。

第七章虚拟变量回归

第七章虚拟变量回归

第七章虚拟变量回归第七章虚拟变量回归第⼀节虚拟变量的性质在实际建模过程中，被解释变量不但受定量变量影响，同时还受定性变量影响。

例如需要考虑性别、民族、不同历史时期、季节差异、政府的更迭（⼯党-保守党）、经济体制的改⾰、固定汇率变为浮动汇率、从战时经济转为和平时期经济等。

这些因素也应该包括在模型中。

⼀、基本概念由于定性变量通常表⽰的是某种特征的有和⽆，所以量化⽅法可采⽤取值为1或0。

这种变量称作虚拟变量（dummy variable ）。

虚拟变量也称：哑元变量、定性变量等等。

通常⽤字母D 或DUM 加以表⽰（英⽂中虚拟或者哑元Dummy 的缩写）。

⽤1表⽰具有某⼀“品质”或属性，⽤0表⽰不具有该“品质”或属性。

虚拟变量使得我们可以将那些⽆法定量化的变量引⼊回归模型中。

虚拟变量应⽤于模型中，对其回归系数的估计与检验⽅法和定量变量相同。

虚拟变量表⽰两分性质，即“是”或“否”，“男”或“⼥”等。

下⾯给出⼏个可以引⼊虚拟变量的例⼦。

例1：你在研究学历和收⼊之间的关系，在你的样本中，既有⼥性⼜有男性，你打算研究在此关系中，性别是否会导致差别。

例2：你在研究某省家庭收⼊和⽀出的关系，采集的样本中既包括农村家庭，⼜包括城镇家庭，你打算研究⼆者的差别。

例3：你在研究通货膨胀的决定因素，在你的观测期中，有些年份政府实⾏了⼀项收⼊政策。

你想检验该政策是否对通货膨胀产⽣影响。

上述各例都可以⽤两种⽅法来解决，⼀种解决⽅法是分别进⾏两类情况的回归，然后看参数是否不同。

另⼀种⽅法是⽤全部观测值作单⼀回归，将定性因素的影响⽤虚拟变量引⼊模型。

⼆、虚拟变量设置规则虚拟变量的设置规则涉及三个⽅⾯: 1.“0”和“1”选取原则虚拟变量取“1”或“0”的原则，应从分析问题的⽬的出发予以界定。

从理论上讲，虚拟变量取“0”值通常代表⽐较的基础类型；⽽虚拟变量取“1”值通常代表被⽐较的类型。

“0”代表基期（⽐较的基础，参照物）；“1”代表报告期（被⽐较的效应）。

EVIEWS虚拟变量模型

EVIEWS虚拟变量模型

虚拟变量【实验目的】掌握虚拟变量的设置方法。

【实验内容】一、试根据表7-1的1998年我国城镇居民人均收入与彩电每百户拥有量的统计资料建立我国城镇居民彩电需求函数；资料来源：据《中国统计年鉴1999》整理计算得到二、试建立我国税收预测模型（数据见实验一）；三、试根据表7-2的资料用混合样本数据建立我国城镇居民消费函数。

资料来源：据《中国统计年鉴》1999－2000整理计算得到【实验步骤】一、我国城镇居民彩电需求函数⒈相关图分析；键入命令：SCAT X Y，则人均收入与彩电拥有量的相关图如7-1所示。

从相关图可以看出，前3个样本点（即低收入家庭）与后5个样本点（中、高收入）的拥有量存在较大差异，因此，为了反映“收入层次”这一定性因素的影响，设置虚拟变量如下：⎩⎨⎧=低收入家庭中、高收入家庭1D图7-1 我国城镇居民人均收入与彩电拥有量相关图⒉构造虚拟变量；方式1：使用DATA 命令直接输入； 方式2：使用SMPL 和GENR 命令直接定义。

DATA D1 GENR XD=X*D1 ⒊估计虚拟变量模型： LS Y C X D1 XD再由t 检验值判断虚拟变量的引入方式，并写出各类家庭的需求函数。

按照以上步骤，虚拟变量模型的估计结果如图7-2所示。

图7-2 我国城镇居民彩电需求的估计我国城镇居民彩电需求函数的估计结果为：i i i i XD D x y0088.08731.310119.061.57ˆ-++= =t (16.249)(9.028) (8.320) (-6.593)2R ＝0.9964 2R ＝0.9937 F ＝366.374 S.E ＝1.066虚拟变量的回归系数的t 检验都是显著的，且模型的拟合优度很高，说明我国城镇居民低收入家庭与中高收入家庭对彩电的消费需求，在截距和斜率上都存在着明显差异，所以以加法和乘法方式引入虚拟变量是合理的。

低收入家庭与中高收入家庭各自的需求函数为：低收入家庭：i i x y0119.061.57ˆ+= 中高收入家庭：()()i i x y0088.00119.08731.3161.57 ˆ-++=i x 003.048.89+= 由此可见我国城镇居民家庭现阶段彩电消费需求的特点：对于人均年收入在3300元以下的低收入家庭，需求量随着收入水平的提高而快速上升，人均年收入每增加1000元，百户拥有量将平均增加12台；对于人均年收入在4100元以上的中高收入家庭，虽然需求量随着收入水平的提高也在增加，但增速趋缓，人均年收入每增加1000元，百户拥有量只增加3台。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

EViews统计分析基础教程
二、含虚拟变量的模型
1.仅含一个虚拟变量
实验：
根据表7-1中的数据显示，建立解释变量为虚拟变量的回归 模型。表中列出了24个不同性别的企业员工的月工资收入情 况，性别一列中“1”表示女性员工，“0”表示男性员工。通 过建立含有虚拟变量的回归模型，试图分析男女平均工资是 否存有差距，如果有差距，那么差距是多少。
二、含虚拟变量的模型
1.仅含一个虚拟变量
EViews统计分析基础教程
二、含虚拟变量的模型
2. 同时含虚拟和定量解释变量
当方程的解释变量中既有虚拟变量又有定量变量时，同样可 以用OLS对模型进行估计。例如：
yt =β0 + β1 xt+β2Dt + μt
EViews统计分析基础教程
二、含虚拟变量的模型
2.虚拟变量
引入虚拟变量的原则：
一般情况下，如果定性变量有m类，并且模型不含有截距项 时，应引入m个虚拟变量；如果模型含有截距项，应引入m1个虚拟变量。
EViews统计分析基础教程
二、含虚拟变量的模型
1.仅含一个虚拟变量
在回归模型中，解释变量可以仅是一个虚拟变量，这样的回 归模型被称为方差分析模型。 例如：
1.仅含一个虚拟变量
实验： 第四步，在工作文件中选择主菜单栏中的“Object”| “New Object” | “Equation”选项，或者选择“Quick”| “Estimate Equation” 选项，打开如下所示的方程对话框。
EViews统计分析基础教程
二、含虚拟变量的模型
1.仅含一个虚拟变量
二、含虚拟变量的模型
2. 同时含虚拟和定量解释变量
操作步骤：
第一步，建立类型为“Unstructured/Undated”（未限定结构/ 未限定日期）的工作文件。
第二步，在该工作文件中建立四个序列对象。 “pc” 代表家 庭拥有的电脑数量；“rev”代表家庭每月收入；“edu”代表 教育程度；“city”表示城乡居民情况。并把相应的数据输入 到每个序列对象中。
EViews统计分析基础教程
一、虚拟变量的定义
2.虚拟变量
定义：
定性变量描述的是变量具有的性质，要将这样的变量纳入回 归模型中，需构造人工变量，从而将定性变量进行量化处理。 在计量经济学中，将取值为“0”和“1” 的人工变量称作虚 拟变量（Dummy Variable），用字母D表示。当D取值为0 时，表示该变量不具备某种属性；当D取值为1时，表示该 变量具有某种属性。
况，xt表示家庭收入， D2 和D3为虚拟解释变量。
EViews统计分析基础教程
二、含虚拟变量的模型
2. 同时含虚拟和定量解释变量
实验： D2 =
1，大专及以上学历 0，其他
1，城镇居民
D3 = 0，非城镇居民
根据表7-2中的数据用普通最小二乘法（OLS）对模型进行 估计，并分析回归结果。
EViews统计分析基础教程
2. 同时含虚拟和定量解释变量
实验：
随着科技的进步和人民生活水平的不断提高，电脑越来越普
及，许多家庭纷纷把个人电脑（PC机）搬进家中。我们可
以研究人们的收入水平、受教育程度与城乡居民之间的关系。
模型如下，
yt =β0 + β1 xt+β2D2t +β3D3t + μt
（t=1，2，…，n）
其中，yt表示根据调查资料所得到的家庭所购买个人电脑情
实验： 在“Equation specification”（方程说明）中列出模型中的被 解释变量、常数项和解释变量。在“Estimation settings”（估 计方法设定）中选择“LS”，用普通最小二乘法对回归模型 进行估计。然后单击“确定”按钮即可得到如下估计结果。
EViews统计分析基础教程
EViews统计分析基础教程
二、含虚拟变量的模型
1.仅含一个虚拟变量
实验：
回归模型为
yt =β0 + β1Dt + μt
（t=1，2，…，n）
其中，yt表示企业员工的工资收入情况，Dt=0表示男性员工，
Dt=1表示女性员工。
EViews统计分析基础教程
二、含虚拟变量的模型
1.仅含一个虚拟变量
实验： 第一步，建立类型为“Unstructured/Undated”（未限定结构/ 未限定日期）的工作文件，在“Data range”（数据范围）中 输入观测数据的样本范围，本例中所分析的数据为24个样本， 在“Names”中为该工资文件命名，如“工资与性别关系”。 然后单击“OK”按钮即可生成工作文件。
EViews统计分析基础教程
二、含虚拟变量的模型
1.仅含一个虚拟变量
实验：
第二步，在该工作文件中建立两个序列对象，一个为 “wage”，一个为“sex”。
输入 “性别”的数据。
EViews统计分析基础教程
二、含虚拟变量的模型
yt =β0 + β1Dt + μt 假设被解释变量yt为员工工资收入，Dt为虚拟解释变量，取 值为0或1：
1，雇员为女性 Dt=
0，雇员为男性
EViews统计分析基础教程
二、含虚拟变量的模型
1.仅含一个虚拟变量
如果该回归模型的随机误差项满足线性回归模型的五个基本 假定条件，则
E（yt| Dt=1）= E（雇员工资收入|雇员为女性）=β0 + β1 E（yt| Dt=0）= E（雇员工资收入|雇员为男性）=β0 β0 + β1表示女性雇员的平均工资收入，β0表示男性雇员的平 均工资收入。
EViews统计分析基础教程
第7章 含虚拟变量的回归模型
重点内容： • 虚拟变量的定义 • 定性变量与定量变量的划分 • 含虚拟变量模型的估计
EViews统计分析基础教程
一、虚拟变量的定义
1.定性变量与定量变量
定量变量：回归模型中有些变量是可以被度量的，如居民消 费、国内生产总值、出口总额等，这些变量被称为“定量变 量”。 定性变量：在经济现象的分析中还存在一些不能被度量的变 量，如性别、种族、婚姻状况、文化程度等，这些变量被称 为“定性变量”。
EViews统计分析基础教程
一、虚拟变量的定义
2.虚拟变量
虚拟变量陷阱：
所谓的“虚拟变量陷阱”是指自变量（解释变量）中包含了 过多的虚拟变量，从而导致了模型出现多重共线性。当模型 中既有整体截距又对每一组都设有一个虚拟变量时，就产生 了虚拟变量陷阱。
EViews统计分析基础教程
一、虚拟变量的定义