EVIEWS虚拟变量模型.pdf
- 格式:pdf
- 大小:255.72 KB
- 文档页数:6

第七讲 经典单方程计量经济学模型:专门问题虚拟变量模型学习目标:1. 了解什么是虚拟变量以及什么是虚拟变量模型;2. 理解虚拟变量的设置原则;3. 掌握虚拟变量模型的两种基本引入方式(加法方式和乘法方式) ;4. 能够自行设计虚拟变量模型,并能够解释其中蕴含的经济意义;教学基本内容一、 虚拟变量 许多经济变量是可以定量度量,例如:商品需求量、价格、收入、产量等; 但有一些影响经济变量的因素是无法定量度量。
例如:职业、性别对收入的影响, 战争、自然灾害对GDP 勺影响,季节对某些产品(如冷饮)销售的影响等。
定性变量:把职业、性别这样无法定量度量的变量称为定性变量。
定量变量:把价格、 收入、销售额这样可以可以定量度量的变量称为定量变 量。
为了能够在模型中能够反映这些因素的影响, 提高模型的精度, 拓展回归模 型的功能,需要将它们“量化”。
这种“量化”通常是通过引入“虚拟变量” 来完成的。
根据这些因素的属性类型, 构造只取“ 0”或“ 1”的人工变量, 通常 称为虚拟变量( dummyvariables ) ,记为 D 。
虚拟变量只作为解释变量。
例如:反映性别的虚拟变量 D1;男0;女般地,基础类型和肯定类型取值为 1;比较类型和否定类型取值为 0虚拟变量的设置原则设置原则:每一定性变量(qualitative variable )所需的虚拟变量个数要比该定性变量的状 态类别数(categories 少1。
即如果有m 种状态,只在模型中引入m-1个虚拟变量例如,冷饮的销售量会受到季节变化的影响。
季节定性变量有春、夏、秋、 冬 4 种状态,只需要设置 3 个虚拟变量:反映文化程度的虚拟变量 D1;本科学历 0;非本科学历E(Y i | X i ,D i 0)1Xi1. 概念虚拟变量模型:同时含有一般解释变量与虚拟变量的模型称为虚拟变量模 型,也称方差分析( 2. 例子(analysis-of varianee: ANOVA )模型。


第七讲 经典单方程计量经济学模型:专门问题虚拟变量模型学习目标:1. 了解什么是虚拟变量以及什么是虚拟变量模型;2. 理解虚拟变量的设置原则;3. 掌握虚拟变量模型的两种基本引入方式(加法方式和乘法方式);4. 能够自行设计虚拟变量模型,并能够解释其中蕴含的经济意义; 教学基本内容一、 虚拟变量许多经济变量是可以定量度量,例如:商品需求量、价格、收入、产量等;但有一些影响经济变量的因素是无法定量度量。
例如:职业、性别对收入的影响,战争、自然灾害对GDP 的影响,季节对某些产品(如冷饮)销售的影响等。
定性变量:把职业、性别这样无法定量度量的变量称为定性变量。
定量变量:把价格、收入、销售额这样可以可以定量度量的变量称为定量变量。
为了能够在模型中能够反映这些因素的影响,提高模型的精度,拓展回归模型的功能,需要将它们“量化”。
这种“量化”通常是通过引入“虚拟变量”来完成的。
根据这些因素的属性类型,构造只取“0”或“1”的人工变量,通常称为虚拟变量(dummy variables ) ,记为D 。
虚拟变量只作为解释变量。
例如:反映性别的虚拟变量⎩⎨⎧=女男;0;1D 反映文化程度的虚拟变量⎩⎨⎧=非本科学历本科学历;0;1D 一般地,基础类型和肯定类型取值为1;比较类型和否定类型取值为0。
二、 虚拟变量的设置原则设置原则:每一定性变量(qualitative variable)所需的虚拟变量个数要比该定性变量的状态类别数(categories)少1。
即如果有m 种状态,只在模型中引入m-1个虚拟变量。
例如,冷饮的销售量会受到季节变化的影响。
季节定性变量有春、夏、秋、冬4种状态,只需要设置3个虚拟变量:⎩⎨⎧=其他春季;0;11D ⎩⎨⎧=其他夏季;0;12D ⎩⎨⎧=其他秋季;0;13D错误设置:⎩⎨⎧=其他春季;0;11D ⎩⎨⎧=其他夏季;0;12D ⎩⎨⎧=其他秋季;0;13D ⎩⎨⎧=其他冬季;0;14D 如果设置第4个虚变量,则出现“虚拟变量陷井”(Dummy Variable Trap )问题。






精品VAR 模型基本操作指引( Eviews )1 、 ADF双序列——打开序列数据窗口——View —— Unit Root Test——位根框(1 st difference,即△ X;intercept:包含截距;trend:包含)界判断:如果ADF 小于某一著性水平下的界,序列在此著性水平下平。
2 、根据 SIC 和 AC 确定 VAR 的滞后期位根操作的出果中3 、建立 VAR 模型在 workfile里——Quick——Estimate VAR⋯——窗缺省的是非束VAR ,另一是向量差修正模型。
出内生量的滞后期。
出用于运算的本范。
Endogenous 要求出VAR 模型中所包括的内生量。
Exogenous要求出外生量(一般包含常数)。
果示中,回系数下第一个括号中的准差,第二个括号中的t 。
4 、脉冲响分析/ 方差分解在行脉冲响函数断之前,需要先VAR模型的平性,用AR根(Inverse Roots of AR Characteristic polunomial)行。
AR根中,如果点都落在位里,才可以做脉冲分析。
如果模型不平,要重新修改量,去掉不著量。
VAR 模型估果窗口中——View —— impulse response——table5、整关系- 可编辑 -精品前提条件:序列同整打开序列数据窗口——View —— Cointegration Test⋯——6、差修正模型Quick —— Estimate VAR⋯——窗——VEC——相比VAR 的置中要多填入差修正个数( Number of CE’s),且此的外生量置中不需要再另外置常数。
—OK7、格杰因果前提条件:序列存在整关系Eviews 可以直接出两个量的双向格杰因果果。
打开数据窗口——View —— Granger Causality⋯——最大滞后度—OK8、建立整回方程建立回模型后,如果模型存在自相关,建立广差分模型- 可编辑 -。

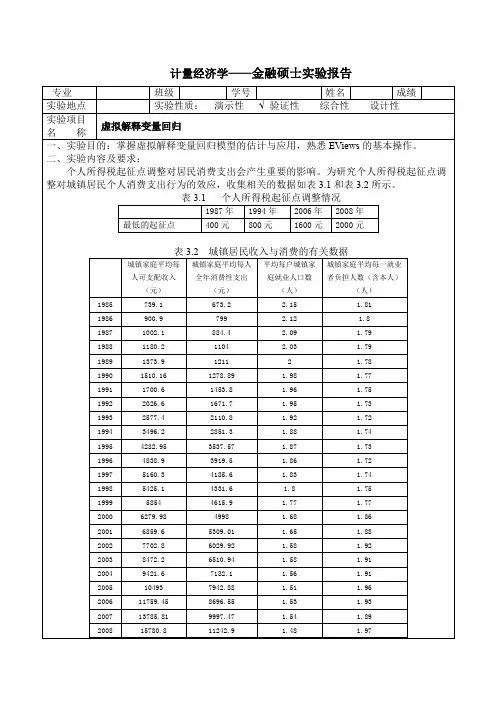
计量经济学——金融硕士实验报告若模型设定为:Consume t=C t+α1Income t+α2Consume t-1+α3Employment t+α4Burden t+α5d1t+α6d2t+α7d3t+α8d4t+εt 其中Consume t表示t期城镇居民家庭人均消费支出,Income t表示t期城镇居民家庭人均可支配收入,Employment t表示t期城镇居民家庭平均每户就业人口,Burden t表示t期城镇居民家庭平均每一就业者负担人数,d it(i=1,2,3,4)相应的虚拟变量。
1)构造用于描述个人所得税调整的虚拟变量,并简要说明其理由;考虑到个人所得税起征点调整对居民消费支出会产生重要的影响,而征税有m=5个不同阶段,故引入m-1=4个虚拟变量d1t,d2t,d3t,d4t。
1985≤t<1987 d1=0d2=0 d3=0d4=01987≤t<1994 d1=1 d2=0 d3=0d4=01994≤t<2006 d1=1 d2=1 d3=0d4=02006≤t<2008 d1=1 d2=1 d3=1 d4=02008≤td1=1 d2=1 d3=1 d4=1因为是个人所得税逐步增多的过程,所以在引入虚拟变量时,是使其在开始实施后依然保留之前的税收。
2)用散点图描述两两变量之间的关系,并给出你对模型设定的结论;①导入数据打开Eviews软件,选择“File”菜单中的“New--Workfile”选项(也可使用命令方式),建立工作文件后,录入数据。
命令格式:DATA income consumemployment burdend1d2d3d4②观测income、employment、burden同consum之间的关系,命令格式:SCAT income consumSCAT employmentconsumSCAT burden consum根据相关关系图,可以认为,consum与income之间存在正相关的线性关系,consum与employment之间存在近似反比例的关系,consum与burden之间的关系图比较混乱,认为可能并不存在相关关系。
虚拟变量【实验目的】掌握虚拟变量的设置方法。
【实验内容】一、试根据表7-1的1998年我国城镇居民人均收入与彩电每百户拥有量的统计资料建立我国城镇居民彩电需求函数;资料来源:据《中国统计年鉴1999》整理计算得到二、试建立我国税收预测模型(数据见实验一);三、试根据表7-2的资料用混合样本数据建立我国城镇居民消费函数。
资料来源:据《中国统计年鉴》1999-2000整理计算得到【实验步骤】一、我国城镇居民彩电需求函数⒈相关图分析;键入命令:SCAT X Y,则人均收入与彩电拥有量的相关图如7-1所示。
从相关图可以看出,前3个样本点(即低收入家庭)与后5个样本点(中、高收入)的拥有量存在较大差异,因此,为了反映“收入层次”这一定性因素的影响,设置虚拟变量如下:⎩⎨⎧=低收入家庭中、高收入家庭1D图7-1 我国城镇居民人均收入与彩电拥有量相关图⒉构造虚拟变量;方式1:使用DATA 命令直接输入; 方式2:使用SMPL 和GENR 命令直接定义。
DATA D1 GENR XD=X*D1 ⒊估计虚拟变量模型: LS Y C X D1 XD再由t 检验值判断虚拟变量的引入方式,并写出各类家庭的需求函数。
按照以上步骤,虚拟变量模型的估计结果如图7-2所示。
图7-2 我国城镇居民彩电需求的估计我国城镇居民彩电需求函数的估计结果为:i i i i XD D x y 0088.08731.310119.061.57ˆ-++==t (16.249)(9.028) (8.320) (-6.593)2R =0.9964 2R =0.9937 F =366.374 S.E =1.066虚拟变量的回归系数的t 检验都是显著的,且模型的拟合优度很高,说明我国城镇居民低收入家庭与中高收入家庭对彩电的消费需求,在截距和斜率上都存在着明显差异,所以以加法和乘法方式引入虚拟变量是合理的。
低收入家庭与中高收入家庭各自的需求函数为:低收入家庭:i i x y0119.061.57ˆ+= 中高收入家庭:()()i i x y0088.00119.08731.3161.57 ˆ-++=i x 003.048.89+= 由此可见我国城镇居民家庭现阶段彩电消费需求的特点:对于人均年收入在3300元以下的低收入家庭,需求量随着收入水平的提高而快速上升,人均年收入每增加1000元,百户拥有量将平均增加12台;对于人均年收入在4100元以上的中高收入家庭,虽然需求量随着收入水平的提高也在增加,但增速趋缓,人均年收入每增加1000元,百户拥有量只增加3台。
虚拟变量
【实验目的】
掌握虚拟变量的设置方法。
【实验内容】
一、试根据表7-1的1998年我国城镇居民人均收入与彩电每百户拥有量的统计资料建立我国城镇居民彩电需求函数;
资料来源:据《中国统计年鉴1999》整理计算得到
二、试建立我国税收预测模型(数据见实验一);
三、试根据表7-2的资料用混合样本数据建立我国城镇居民消费函数。
资料来源:据《中国统计年鉴》1999-2000整理计算得到
【实验步骤】
一、我国城镇居民彩电需求函数
⒈相关图分析;
键入命令:SCAT X Y,则人均收入与彩电拥有量的相关图如7-1所示。
从相关图可以看出,前3个样本点(即低收入家庭)与后5个样本点(中、
高收入)的拥有量存在较大差异,因此,为了反映“收入层次”这一定性因素的影响,设置虚拟变量如下:
⎩⎨
⎧=低收入家庭
中、高收入家庭
1D
图7-1 我国城镇居民人均收入与彩电拥有量相关图
⒉构造虚拟变量;
方式1:使用DATA 命令直接输入; 方式2:使用SMPL 和GENR 命令直接定义。
DATA D1 GENR XD=X*D1 ⒊估计虚拟变量模型: LS Y C X D1 XD
再由t 检验值判断虚拟变量的引入方式,并写出各类家庭的需求函数。
按照以上步骤,虚拟变量模型的估计结果如图7-2所示。
图7-2 我国城镇居民彩电需求的估计
我国城镇居民彩电需求函数的估计结果为:
i i i i XD D x y
0088.08731.310119.061.57ˆ−++= =t (16.249)(9.028) (8.320) (-6.593)
2R =0.9964 2R =0.9937 F =366.374 S.E =1.066
虚拟变量的回归系数的t 检验都是显著的,且模型的拟合优度很高,说明我国城镇居民低收入家庭与中高收入家庭对彩电的消费需求,在截距和斜率上都存在着明显差异,所以以加法和乘法方式引入虚拟变量是合理的。
低收入家庭与中高收入家庭各自的需求函数为:
低收入家庭:
i i x y
0119.061.57ˆ+= 中高收入家庭:
()()i i x y
0088.00119.08731.3161.57 ˆ−++=i x 003.048.89+= 由此可见我国城镇居民家庭现阶段彩电消费需求的特点:对于人均年收入在3300元以下的低收入家庭,需求量随着收入水平的提高而快速上升,人均年收入每增加1000元,百户拥有量将平均增加12台;对于人均年收入在4100元以上的中高收入家庭,虽然需求量随着收入水平的提高也在增加,但增速趋缓,人均年收入每增加1000元,百户拥有量只增加3台。
事实上,现阶段我国城镇居民中国收入家庭的彩电普及率已达到百分之百,所以对彩电的消费需求处于更新换代阶段。
二、我国税收预测模型
要求:设置虚拟变量反映1996年税收政策的影响。
方法:取虚拟变量D1=1(1996年以后),D1=0(1996年以前)。
键入命令:GENR XD=X*D1
LS Y C X D1 XD
则模型估计的相关信息如图7-3所示。
图7-3 引入虚拟变量后的我国税收预测模型
我国税收预测函数的估计结果为:
i i i i XD D x y
12139.0198.819508286.0268.1234ˆ+−+= =t (24.748) (47.949) (-10.329) (11.208)
2R =0.9990 2R =0.9987 F =3332.429 S.E =87.317
可见,虚拟变量的回归系数的t 检验都是显著的,且模型的拟合优度很高,说明1996年的税收政策对税收收入在截距和斜率上都产生了明显影响。
1996年前的税收函数为:
i i x y
08286.0268.1234ˆ+= 1996年后的税收函数为:
i i x y
20425.093.6960ˆ+−= 由此可见,在实施1996年的税收政策前,国内生产总值每增加10000元,税收收入增加828.6元;而1996年后,国内生产总值每增加10000元,税收收入则增加2042.5元,因此,1996年的税收政策大大提高了税收收入水平。
三、我国城镇居民消费函数 要求:
⒈利用虚拟变量分析两年的消费函数是否有显著差异; ⒉利用混合样本建立我国城镇居民消费函数。
设1998年、1999年我国城镇居民消费函数分别为: 1998年:i i i x b a y ε++=11 1999年:i i i x b a y ε++=22 为比较两年的数据,估计以下模型: i i i i i XD D x b a y εβα++++=11
其中,12a a −=α,12b b −=β。
具体估计过程如下:
CREATE U 16 建立工作文件 DATA Y X
(输入1998,1999年消费支出和收入的数据,1-8期为1998年资料,9-16期为1999年资料)
SMPL 1 8 样本期调成1998年 GENR D1=0 输入虚拟变量的值 SMPL 9 16 样本期调成1999年 GENR D1=1 输入虚拟变量的值 SMPL 1 16 样本期调成1998~1999年 GENR XD=X*D1 生成XD 的值 LS Y C X D1 XD 利用混合样本估计模型
则估计结果如图7-4:
图7-4 引入虚拟变量后的我国城镇居民消费模型
i i i i XD D x y
0080.01917.616237.070588.924ˆ−++= =t (10.776) (43.591) (0.510) (-0.417)
2R =0.9972 2R =0.9965 F =1411.331 S.E =113.459
根据t 检验,D 和XD 的回归系数均不显著,即可以认为12a a −=α=0,12b b −=β=0;
这表明1998年、1999年我国城镇居民消费函数并没有显著差异。
因此,可以将两年的样本数据合并成一个样本,估计城镇居民的消费函数。
独立样本回归与混合样本回归结果如图7-5~图7-7所示。
图7-5 1998年样本回归的我国城镇居民消费模型
图7-6 1999年样本回归的我国城镇居民消费模型
图7-7 混合样本回归的我国城镇居民消费模型
将不同样本估计的消费函数结果列在表7-3中,可以看出,使用混合回归明显地降低了系数的估计误差。
()b Sˆ2R 样本aˆbˆ()a Sˆ
1998~1999年955.67 0.6195 55.91 0.0089 0.9971 1998年924.71 0.6237 86.43 0.0144 0.9968 1999年985.9 0.6157 83.21 0.0127 0.9974。