下载文档原格式
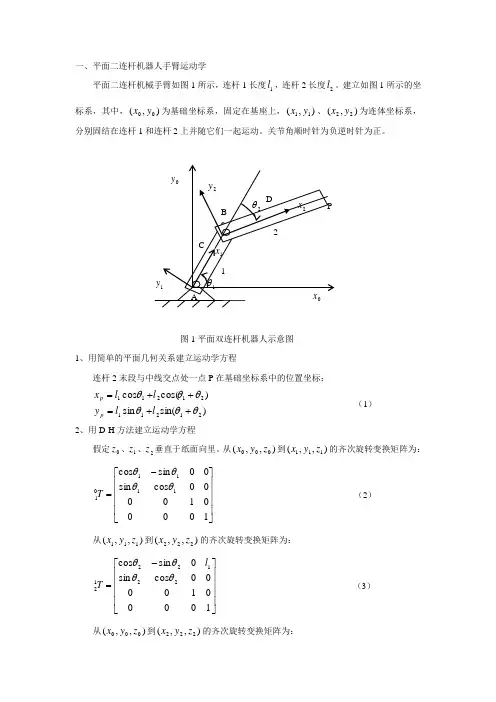
一、平面二连杆机器人手臂运动学平面二连杆机械手臂如图1所示，连杆1长度1l ，连杆2长度2l 。
建立如图1所示的坐标系，其中，),(00y x 为基础坐标系，固定在基座上，),(11y x 、),(22y x 为连体坐标系，分别固结在连杆1和连杆2上并随它们一起运动。
关节角顺时针为负逆时针为正。
图1平面双连杆机器人示意图 1、用简单的平面几何关系建立运动学方程连杆2末段与中线交点处一点P 在基础坐标系中的位置坐标：)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p （1）2、用D-H 方法建立运动学方程假定0z 、1z 、2z 垂直于纸面向里。
从),,(000z y x 到),,(111z y x 的齐次旋转变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 00sin cos 111101θθθθT （2） 从),,(111z y x 到),,(222z y x 的齐次旋转变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 0sin cos 2212212θθθθl T （3） 从),,(000z y x 到),,(222z y x 的齐次旋转变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⋅=10000100sin 0)cos()sin(cos 0)sin()cos(1000010000cos sin 0sin cos 1000010000cos sin 00sin cos 112121112121221221111120102θθθθθθθθθθθθθθθθθθl l l T T T （4）那么，连杆2末段与中线交点处一点P 在基础坐标系中的位置矢量为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⋅=110)sin(sin )cos(cos 10010000100sin 0)cos()sin(cos 0)sin()cos(212112121121121211121212020p p p z y x l l l l l l l P T P θθθθθθθθθθθθθθθθ （5）即，)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p （6）与用简单的平面几何关系建立运动学方程（1）相同。
简述机器人雅可比矩阵的概念机器人雅可比矩阵是机器人控制理论中的一个重要概念，它描述了机器人末端执行器在关节空间和笛卡尔空间中的运动学关系。
本文将从机器人运动学的基本概念入手，介绍雅可比矩阵的定义、性质和应用，以及在机器人控制中的重要作用。
一、机器人运动学基本概念机器人运动学是研究机器人运动规律和运动参数的学科，它是机器人控制理论的重要组成部分。
机器人运动学主要分为正运动学和逆运动学两个部分。
正运动学是指通过机器人关节角度计算机器人末端执行器的位置和姿态，即把关节空间的运动状态转换为笛卡尔空间的运动状态。
逆运动学则是指通过机器人末端执行器的位置和姿态计算机器人关节角度，即把笛卡尔空间的运动状态转换为关节空间的运动状态。
正逆运动学是机器人控制中的基本问题，也是机器人实际应用中必须解决的问题。
机器人运动学中的基本概念包括机器人坐标系、机器人关节角度、机器人末端执行器的位置和姿态等。
机器人坐标系是机器人运动学中的一个基本概念，它是描述机器人运动状态的基础。
机器人坐标系可以分为基座坐标系和工具坐标系两种类型。
基座坐标系是机器人的固定参考系，通常与机器人底座相对应。
工具坐标系则是机器人末端执行器的参考系，通常与机器人末端执行器的位置和姿态相对应。
机器人关节角度是机器人运动学中的另一个基本概念，它是描述机器人关节运动状态的参数。
机器人关节角度通常用关节角度向量表示，例如q=[q1, q2, ..., qn]T，其中n是机器人关节数量。
机器人关节角度向量是机器人控制中的重要参数，它可以用来控制机器人的关节运动状态。
机器人末端执行器的位置和姿态是机器人运动学中的另一个基本概念，它是描述机器人末端执行器运动状态的参数。
机器人末端执行器的位置通常用位置向量表示，例如p=[x, y, z]T，其中x、y、z 是机器人末端执行器在笛卡尔空间中的位置坐标。
机器人末端执行器的姿态通常用姿态矩阵或欧拉角表示，例如R=[r11, r12, r13; r21, r22, r23; r31, r32, r33]，其中r11、r12、r13、r21、r22、r23、r31、r32、r33是姿态矩阵的元素。
一、平面二连杆机器人手臂运动学平面二连杆机械手臂如图1所示，连杆1长度1l ，连杆2长度2l 。
建立如图1所示的坐标系，其中，),(00y x 为基础坐标系，固定在基座上，),(11y x 、),(22y x 为连体坐标系，分别固结在连杆1和连杆2上并随它们一起运动。
关节角顺时针为负逆时针为正。
图1平面双连杆机器人示意图 1、用简单的平面几何关系建立运动学方程连杆2末段与中线交点处一点P 在基础坐标系中的位置坐标：)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p （1）2、用D-H 方法建立运动学方程假定0z 、1z 、2z 垂直于纸面向里。
从),,(000z y x 到),,(111z y x 的齐次旋转变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 00sin cos 111101θθθθT （2） 从),,(111z y x 到),,(222z y x 的齐次旋转变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100010000cos sin 0sin cos 2212212θθθθl T （3） 从),,(000z y x 到),,(222z y x 的齐次旋转变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⋅=10000100sin 0)cos()sin(cos 0)sin()cos(1000010000cos sin 0sin cos 1000010000cos sin 00sin cos 112121112121221221111120102θθθθθθθθθθθθθθθθθθl l l T T T （4）那么，连杆2末段与中线交点处一点P 在基础坐标系中的位置矢量为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⋅=110)sin(sin )cos(cos 10010000100sin 0)cos()sin(cos 0)sin()cos(212112121121121211121212020p p p z y x l l l l l l l P T P θθθθθθθθθθθθθθθθ （5）即，)sin(sin )cos(cos 2121121211θθθθθθ++=++=l l y l l x p p （6）与用简单的平面几何关系建立运动学方程（1）相同。
机器人雅可比矩阵简介机器人雅可比矩阵（Robot Jacobian Matrix）是机器人运动学中的重要概念之一。
它描述了机器人末端执行器的速度与关节速度之间的关系，是机器人运动方程求解、运动规划和控制的基础。
本文将详细介绍机器人雅可比矩阵的定义、性质以及它在机器人学中的应用。
定义在介绍机器人雅可比矩阵之前，我们先回顾一下机器人运动学的基本概念。
假设有一个机器人系统，它由n个自由度的关节组成，每个关节的转动由关节角度表示。
而机器人的末端执行器的位置和姿态可以通过正向运动学求解得到，位置用笛卡尔坐标表示，姿态用旋转矩阵或四元数表示。
机器人雅可比矩阵描述了机器人末端执行器的速度与关节速度之间的关系。
具体来说，设机器人关节速度为q_dot，末端执行器速度为x_dot，机器人雅可比矩阵为J，那么雅可比矩阵满足以下关系：x_dot = J * q_dot性质机器人雅可比矩阵具有以下几个重要的性质：1.雅可比矩阵的维度为6×n，其中6表示笛卡尔坐标的维度，n表示机器人的自由度数。
2.雅可比矩阵是一个矩阵函数，它的元素可以表示为：J_ij = ∂f_i / ∂q_j其中，f_i表示末端执行器的第i个度量值，q_j表示第j个关节角度。
3.雅可比矩阵的每一列表示末端执行器在各个关节速度方向上的运动灵敏度。
如果某列的元素值较大，说明在该关节角度变化时，末端执行器的运动会更加敏感。
4.雅可比矩阵的秩决定了机器人在不同姿态下所能达到的运动自由度。
如果雅可比矩阵的秩小于n，那么机器人在某些姿态下会出现奇异配置，并且无法实现所需的末端执行器速度。
应用机器人雅可比矩阵在机器人学中有着广泛的应用。
下面介绍几个常见的应用场景：逆运动学求解在机器人学中，逆运动学是指已知末端执行器的位置和姿态，求解机器人关节角度的过程。
雅可比矩阵在逆运动学求解中起到了关键作用。
通过雅可比矩阵的逆矩阵，可以将末端执行器的速度映射到关节速度空间中，进而求解出关节速度。
题型：填空名词解释简答计算第一章定义：机器人是一种用于移动各种材料、零件、工具或专用装置，通过可编程序动作来执行种种任务并具有编程能力的多功能机械手。
特征：1）机器人的动作机构具有类似于人或其他生物体某些器官（肢体、感官等）的功能2）机器人具有通用性，工作种类多样，动作程序灵活多变。
3）机器人具有不同程度的智能性，如记忆、感知、推理、决策、学习等。
4）机器人具有独立性，完整的机器人系统在工作中可以不依赖于人的干预。
1.2工业机器人与数控机床有什么区别？1）机器人的运动为开式运动链而数控机床为闭式运动链2）工业机器人一般具有多关节，数控机床一般无关节且均为直角坐标系统3）工业机器人是用于工业中各种作业的自动化机器而数控机床应用于冷加工;4）机器人灵活性好，数控机床灵活性差。
1.4说明工业机器人的基本组成及三大部分之间的关系答:工业机器人由三个部分，六个子系统组成，这三个部分分别是机械部分、传感部分、控制部分；六个子系统分别是驱动系统、机械系统、感知系统、控制系统、机器人-环境交互系统和人机交互系统等。
他们的关系如下图所示：人机履叙|Jsta+s宦*»31.5简述下面几个术语的含义：自由度、重复定位精度、工作范围、最大工作速度、承载能力。
芥：门市度是机器人所典仃的独立坐标运动的数目，不包括于爪（衣瑞执行器）的开介门由度*重宣定位精度是关于精度的统计数据，指机器人重良到达某一确定位置准确的概率，是蛋复同…位置的范围.可以用各次不同位置平均值的偏差來表示•工作范围是指机器人乎臂末端或手腕中心所能到达的所有点的渠合，也叫工作区域。
「•作速度一般指最大T作速度，可以足指口由度匕最大的稳定速度，也可以定义为于臂末端垃人的合成速度〔通常在技术参数中加以说明人承我能力是指机器人在工作范尉内的任何位姿匕所能承受的址大质晟.从运动学的观点看，完成一特定作业时具有多余自由度的机器人称为冗余自由度机器人。
1.9工业机器人怎样按控制方式来分类？点位控制连续轨迹控制补充：按机器人的结构形式分类1、按坐标形式分类直角坐标型机器人、圆柱坐标型机器人球坐标型机器人、关节坐标型机器人2、按控制方式来分类点位控制连续轨迹控制3、按驱动方式分类气力驱动式、液力驱动式、电力驱动式、新型驱动式工业机器人的机械系统由机身、手臂、末端执行器三大件组成。
并联机器人的雅可比，可操作性，条件数和精度（翻译论文）虽然在最早的机器人研究中就已经有了雅可比矩阵的概念、可操纵性、条件数的概念，但是它们的真正意义并不是很好理解。
在本文中，我们重新审视这些作为并联机器人优化设计精度指标的概念。
首先，我们指出，通常的雅可比矩阵的输入—输入方程可能不足以分析平台的定位误差。
然后我们检验可操纵性的概念，表明其经典的解释是错误的。
我们考虑各种常见的局部灵巧指数，其中大部分是基于雅可比矩阵的条件数。
值得注意的是，即使对于一个给定的机器人，在一个特定的姿态也会有各种各样的条件数，这些条件数之间都不一致，和我们想得到的精度指标也不一致。
然后考虑了全局调节指数。
除了存在基于错误的局部准确性指数的问题外，还有一个忽略了大部分时间而进行计算的计算问题。
最后，我们检验了其他哪些指标可用于优化设计，并且介绍了计算它们的难度。
1 引言我们将使用一个相对通用的非冗余并联机构的定义。
当一个机构用至少两个运动链来控制自由度n<6的末端执行器时，我们定义它为并联机构，而其他的6-n 个自由度是一个恒定值通过单自由度驱动关节控制。
此外，如果将驱动器锁定，则末端执行器的自由度为0，非驱动关节有一个单自由度。
这样的定义涵盖了经典的六自由度机器人，比如Gough 和Hexa 平台，还有少于六自由度的机构，如Delta 和3-UPU 机构。
如今，并联机构的应用领域越来越广，如望远镜、精定位装置、包装速度快、机床、医疗。
对尺寸非常的敏感是并联机构优化设计的一个关键问题。
最优设计的方法有静力学性能指标。
精度显然是许多应用中的一个关键问题。
并联机构也有串联机构的一些关键问题，因此，针对这些问题做了很多广泛的研究，定义除了很多准确性指标，这些结果已经应用到并联机构上。
本文的目的是检验这些指标是否适用于并联机构。
雅可比矩阵和逆雅可比矩阵用于研究末端执行器的定位精度的，为了这个目的，很有必要研究它们的概念。
机器人动力学雅克比-概述说明以及解释1.引言1.1 概述机器人动力学是研究机器人运动过程中的力学和动力学特性的学科，主要涉及机器人的姿态、速度、加速度、力和力矩等相关物理量。
机器人动力学一直以来都是机器人领域的关键问题之一，对于机器人的运动控制和路径规划具有重要的指导意义。
雅克比矩阵是机器人动力学中一项关键的工具，用于描述机器人多自由度系统中各关节之间的运动传递关系。
通过雅克比矩阵，我们可以计算出机器人末端执行器在给定关节角速度下的线速度和角速度，从而实现对机器人运动的精确控制。
机器人动力学的研究在实际应用中有着广泛的意义。
首先，深入理解机器人的动力学特性可以帮助我们设计出更加高效、灵活的机器人控制算法，从而提升机器人的运动精度和速度。
其次，机器人动力学的研究还可以为机器人路径规划、障碍物避障等问题提供重要的理论支持和指导。
此外，随着机器人应用领域的拓展，如医疗、教育、家庭服务等，机器人动力学的研究也将在未来发挥更加重要的作用。
总结起来，机器人动力学是研究机器人运动特性的学科，雅克比矩阵则是机器人动力学中的重要工具。
通过研究和应用机器人动力学，我们可以实现对机器人运动的精确控制，提升机器人的运动效率和准确性，并且为机器人的应用和发展打下坚实的基础。
未来，机器人动力学的研究将随着机器人技术的不断发展而不断探索新的方向，并为更广泛的机器人应用提供理论支持和指导。
1.2 文章结构文章结构部分的内容应当包括对整篇文章的组织和章节安排进行介绍。
可以按照以下方式编写文章结构的内容：2. 文章结构本文共分为以下几个部分：引言、正文和结论。
2.1 引言部分将对机器人动力学的概念进行概述，介绍机器人动力学的背景和意义。
在此部分还将阐述本文的目的和结构。
2.2 正文部分将重点讨论雅克比矩阵的概念和应用。
首先，将介绍雅克比矩阵的定义和性质，以及其在机器人动力学中的重要作用。
接着，将探讨雅克比矩阵在路径规划、运动控制和力学分析等方面的应用。
中国科学技术科学一月2010卷53号：168−174DOI：10.1007/s11431-009-0375-y 一种基于尺寸均匀的雅可比矩阵的三自由度并联机械手孙涛，宋逸民，李永刚，刘林山天津大学机械工程学院，天津300072，1，中国；天津工程师范学院机械工程学院，天津300222，2，中国2009年5月18日收到，2009年8月19日接受对三自由度的平移和旋转耦合并联机械手进行了研究。
机械手的结构是由一个移动平台通过三个相同的系统连接到一个固定的基地（棱镜转动球形）串行的四肢，其独特的拓扑结构，导致传统的雅可比矩阵的物理单元的不一致和寄生运动的出现。
本文介绍了一种基于尺寸均匀的雅可比矩阵的条件下，机械手的kinetostatic性能指标后，上述机器人工作空间的搜索和分析的关键设计变量对工作空间的影响。
最后，提出了一种机械手的尺寸的合成方法，它可以看作是一个主题的寄生运动和其他一些工程约束的非线性规划问题。
PKMS（并联运动机床），三维合成，尺寸均匀的雅可比，3-PRS机械手，工作区。
引用：孙涛，宋逸民，李永刚等。
三维合成基于三维均匀雅可比矩阵三自由度并联机器人。
中国技术科学，2010，53：168-174，DOI：10.1007/s11431-009-0375-y1 引言有限的自由度（自由度）PKMS （并联机床）的发展一直是研究的热点，由于案情PKMS的深入浅出结构，成本较低，易于控制等一系列与6自由度PKMS比较。
平移和旋转耦合的有限自由度PKMS的外观和应用提供了用于制造或装配在飞机和汽车行业大型零件的瓶颈问题的选项。
举例来说，一个精心设计的有限自由度并联机床具有平移和旋转的耦合可能被集成到数控加工单元作为一个插件和播放模块，它可以沿着一个超长轨道或其他辅助设备在大型驱动飞机和汽车零部件加工或组装。
与平移和旋转耦合的有限自由度PKMS的杰出代表，在3 -PRS（棱柱回转球面）机器人已经应用到很多方面，因为结构紧凑，出色的运动学和动力学性能，例如，由DS技术公司[ 1著名短跑Z3头，2 ]在德国，以及参考文献[ 3 ]最初提出的望远镜中的应用，等等。
逆运动学雅可比矩阵逆运动学雅可比矩阵是机器人学中的重要概念，用于描述机器人末端执行器的运动学性质。
通过逆运动学雅可比矩阵，我们可以推导出机器人在给定末端执行器速度时，关节的运动速度。
本文将介绍逆运动学雅可比矩阵的定义、推导方法和应用场景。
逆运动学雅可比矩阵是描述机器人末端执行器速度与关节速度之间关系的矩阵。
在机器人学中，关节速度是指机器人各个关节的运动速度，末端执行器速度是指机器人末端执行器在笛卡尔坐标系下的速度。
逆运动学雅可比矩阵将这两种速度联系起来，帮助我们理解机器人的运动学特性。
逆运动学雅可比矩阵的定义如下：假设机器人有n个关节，末端执行器在笛卡尔坐标系下的速度为v，关节速度为q̇，则逆运动学雅可比矩阵J的定义如下所示：J = (∂f/∂q̇)⁻¹其中，f表示末端执行器的位置和姿态函数，∂f/∂q̇表示末端执行器速度对关节速度的偏导数。
逆运动学雅可比矩阵的维度为6xN，其中N表示机器人关节数量。
在推导逆运动学雅可比矩阵时，我们可以使用几何法或微分法。
几何法是基于坐标变换和几何关系的推导方法，而微分法则是基于微分运算的推导方法。
这两种方法在不同情况下都有其适用性。
逆运动学雅可比矩阵在机器人学中有广泛的应用。
首先，逆运动学雅可比矩阵可以用于机器人轨迹规划和路径优化。
通过计算机器人末端执行器速度和关节速度的关系，我们可以优化机器人的运动轨迹，使其更加平滑和高效。
逆运动学雅可比矩阵还可以用于机器人的运动控制和力控制。
通过控制机器人的关节速度，我们可以实现对机器人末端执行器的精确控制。
在力控制中，逆运动学雅可比矩阵可以帮助我们估计机器人末端执行器受到的外部力和力矩，并进行相应的控制。
逆运动学雅可比矩阵还可以用于机器人的碰撞检测和避障。
通过计算机器人末端执行器速度和关节速度的关系，我们可以判断机器人是否会与周围环境发生碰撞，并采取相应的避障策略。
总结起来，逆运动学雅可比矩阵是机器人学中的重要概念，用于描述机器人末端执行器的运动学性质。
精心整理
一、平面二连杆机器人手臂运动学
平面二连杆机械手臂如图1所示，连杆1长度1l ，连杆2长度2l ，连杆3长度为3l 。
建立如图1所示的坐标系，其中，),(00y x 为基础坐标系，固定在基座上，),(11y x 、),(22y x 、33(,)x y 为连体坐标系，分别固结在连杆1、连杆2、连杆3上并随它们一起运动。
关节角顺时针为负逆时针为正。
1
θ
图11112123123p p x y 2、用D-H 方法建立运动学方程
假定0z 、1z 、2z 垂直于纸面向外。
从),,(000z y x 到),,(111z y x 的齐次旋转变换矩阵为：
⎥⎥
⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡-=100
010000cos sin 00sin cos 1
11101
θθ
θθT （2）
从),,(111z y x 到),,(222z y x 的齐次旋转变换矩阵为：
⎥⎥
⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡-=100
010000cos sin 0sin cos 2
212212θθ
θθl T （3） 从222(,,)x y z 到333(,,)x y z 的齐次旋转变换矩阵为：
33212cos sin 0l T θθ-⎡⎤⎢⎥=从(003T =003P =结论：（6）与用简单的平面几何关系建立运动学方程（1）相同。
补充：正解用于仿真，逆解用于控制
建立以上运动学方程后，若已知个连杆的关节角123θθθ、、，就可以用运动学方程求出机械手臂末端位置坐标，这可以用于运动学仿真。
3、平面二连杆机器人手臂逆运动学
二、平面二连杆机器人手臂的速度雅可比矩阵
速度雅可比矩阵的定义：从关节速度向末端操作速度的线性变换。
现已二连杆平面机器人为例推导速度雅可比矩阵。
上面的运动学方程两边对时间求导，得到下面的速度表达式：
111212123123123111212122123123sin sin()()sin()()cos cos()()cos()()
p p dx l l l dt dy l l l dt
θθθθθθθθθθθθθθθθθθθθθθθθ=-⋅-+⋅+-++⋅++=⋅++⋅++++⋅++（17）
把上式写成如下的矩阵形式：
⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡++++-+--=⎥⎦⎤⎢⎣⎡21
2122121121221211)cos()cos(
cos )sin()sin(sin θθθθθθθθθθθθ l l l l l l y x p p （18） 令上式中的末端位置速度矢量X
x p =⎥⎤⎢⎡， 矩阵1
1l l ⎢⎣⎡-(1θJ
1(J θ2122
22211211θ∂J J J J 由此可知雅可比矩阵的定义：
⎥⎥⎥
⎥⎦
⎤
⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂=⎥⎦⎤⎢⎣⎡=21
21
2221
1211
21),(θθθθθθp p p p
J y y x x J J J
J （21） 三、平面二连杆机器人手臂的动力学方程
推倒动力学方程的方法很多，各有优缺点。
拉格朗日方法思路清晰、不考虑连杆之间的内力，是推倒动力学方程的常用方法。
下面推导图1所示的平面双连杆机器人的动力学方程。
图1中所示连杆均为均质杆，其转动惯量分别是1I 和2I 。
1、求两连杆的拉格朗日函数 （1）求系统总动能
连杆1的动能为：
2121121211211
1)1(12
1θθθ l m l m I K A ===
（21）
y x D D Y x D D （122(21121(2121l m I K ===
212212222222222122122222112122
122122222222212212
22121)cos 2131(61)cos 21616121()cos 32(2161)cos 31(21θθθθθθθθθθθθ l l m l m l m l l m l m l m l m l l l m l m l l l l m K K ++++++=+++++=
=（26） （2）求系统总势能 系统总势能为：
))sin(2
1
sin (sin 21212112111θθθθ+++=l l g m gl m P （27）
（3）求拉格朗日函数
)]sin(2
1
sin [sin 21)cos 2131(61)cos 21616121(21211211121221222222222212212222211212θθθθθθθθθθ++--++++++=-=l l g m gl m l l m l m l m l l m l m l m l m P
K L （28） （4）列写动力学方程
按照拉格朗日方程，对应关节1、2的驱动力矩分别为：
211
1τθθτ∂-
∂∂∂∂=∂∂-∂∂∂∂=
L
L t L
L t （29）
(21τ-=l m ）
同理：
2τ=（32）
轨迹规以及 用三直角坐标空间的轨迹规划（1）所有用于关节空间的轨迹规划方法都可以用于直角坐标空间轨迹规划；（2）直角坐标轨迹规划必须不断进行逆运动学运算，以便及时得到关节角。
这个过程可以归纳为以下计算循环：
（a ）将时间增加一个增量；
（b ）利用所选择的轨迹函数计算出手的位姿； （c ）利用逆运动学方程计算相应的关节变量； （d ）将关节变量信息送给控制器； （e ）返回到循环的开始。
五、二连杆机器人的控制。
