答案第2章 电阻电路的等效变换(含答案)

电路习题解答第一章 电路模型和电路定律【题1】：由U A B =5V 可得：I AC .=-25A ：U D B =0：U S .=125V 。

【题2】：D 。

【题3】：300；-100。

【题4】：D 。

【题5】：()a i i i =-12；()b u u u =-12；()c ()u u i i R =--S S S ；()d ()i i R u u =--S SS 1。

【题6】：3；-5；-8。

【题7】：D 。

【题8】：P US1=50 W ；P U S 26=- W ；P U S 3=0；P I S 115=- W ；P I S 2 W =-14；P I S 315=- W 。

【题9】：C 。

【题10】：3；-3。

【题11】：-5；-13。

【题12】：4（吸收）；25。

【题13】：0.4。

【题14】：3123I +⨯=；I =13A 。

【题15】：I 43=A ；I 23=-A ；I 31=-A ；I 54=-A 。

【题16】：I =-7A ；U =-35V ；X 元件吸收的功率为P U I =-=-245W 。

【题17】：由图可得U E B =4V ；流过2 Ω电阻的电流I E B =2A ；由回路ADEBCA 列KVL 得 U I A C =-23；又由节点D 列KCL 得I I C D =-4；由回路CDEC 列KVL 解得；I =3；代入上 式，得U A C =-7V 。

【题18】：P P I I 12122222==；故I I 1222=；I I 12=； ⑴ KCL ：43211-=I I ；I 185=A ；U I I S =-⨯=218511V 或16.V ；或I I 12=-。

⑵ KCL ：43211-=-I I ；I 18=-A ；U S =-24V 。

第二章电阻电路的等效变换【题1】：[解答]I=-+9473A=0.5A；U Ia b.=+=9485V；IU162125=-=a b.A；P=⨯6125.W=7.5W；吸收功率7.5W。

答案及解析115答案第一章电路模型和电路定律【题1】：由U A B 5 V 可得：IA C 2.5 A：U DB 0 ：U S 125. V。

【题2】：D。

【题3】：300；-100。

【题4】：D。

【题5】： a i i 1 i 2 ； b u u1 u2 ； c u u S i i S R S ； d i iS1RSu u S 。

【题6】：3；-5；-8。

【题7】：D。

【题8】：PU S 1 50 W ；P U S 2 6 W ；P U S3 0 ；P I S 1 15 W ；P I S2 14 W ；P I S 3 15 W 。

【题9】：C。

【题10】：3；-3。

【题11】：-5；-13。

【题12】：4（吸收）；25。

【题13】：0.4。

1【题14】：3 I 1 2 3 ；IA 。

3【题15】：I 4 3 A；I 2 3 A；I 3 1A；I 5 4 A。

【题16】：I 7 A；U 35 V；X 元件吸收的功率为P U I 245 W。

【题17】：由图可得U E B 4 V；流过 2 电阻的电流I E B 2 A；由回路ADEBCA 列KVL 得U A C 2 3I ；又由节点 D 列KCL 得I C D 4 I ；由回路CDEC 列KVL 解得；I 3 ；代入上式，得U A C 7 V。

【题18】：P1 P2 2 II212222 ；故I I122；I 1 I 2 ；⑴KCL：43I I ；I 11 12858A；U I 1 I 1 V 或 1.6 V；或I 1 I2 。

S 2 15⑵KCL：43I I ；I1 121 8 A；U S 24V。

第二章电阻电路的等效变换【题1】：[解答]I9 47 3ab 9 4 8.5 V；A =0 .5 A ；U II 1 U 6ab . A ；P 6 1.2 5 W = 7 .5 W ；吸1 252收功率7.5W。

【题2】：[解答]【题3】：[解答] C。

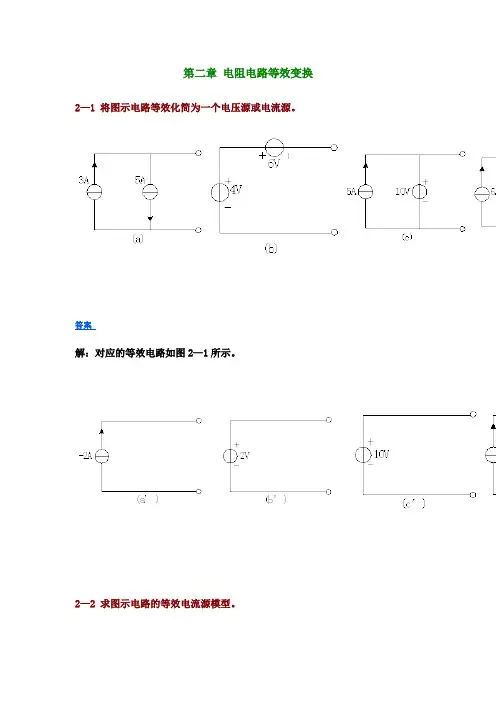
第二章电阻电路等效变换2—1 将图示电路等效化简为一个电压源或电流源。

答案解：对应的等效电路如图2—1所示。

2—2 求图示电路的等效电流源模型。

答案解：对应的等效电路如图2—2所示，其中（d）不存在等效的电流源模型。

2—3 求图示电路的等效电源模型。

答案解：对应的等效电路如图2—3所示，其中（d）不存在等效的电压源模型。

2—4 图示电路，求i、u和R。

ab答案解：（a ）经等效变换后，可得到右示（a’）电路。

（b ）经等效变换后，可得到右示（b’）电路。

2—5 图示电路，求i 。

答案解：电路（a ）经等效变换后，可得到（b ）图电路。

2—6 图示电路，求i、u。

s答案解：原电路经等效变换后，可得到2—6右示电路。

2—7 图示电路，求输入电阻R。

O答案解：原电路经△—Υ等效变换可得到2—7所示对应电路，其中：（a ）（b ）（c ）2—8 证明图（a）和图（b）电路是等效的。

答案证明：图（a）和图（b）电路等效变换过程如图2—8所示：所以，图（a）和图（b）电路等效。

（注：等效电路并不唯一）2—9 图示电路，求电压uab ,ucb。

答案解：2—10 图示电路，求电压u。

答案解：原电路经等效变换后，可得到下图所示电路，由此可得：2—11 图示电路，求电压R 。

已知u 1=1V 。

答案解：2—12 图示电路，求u。

3答案解：2—13 图示电路，求u 3。

答案 解：。

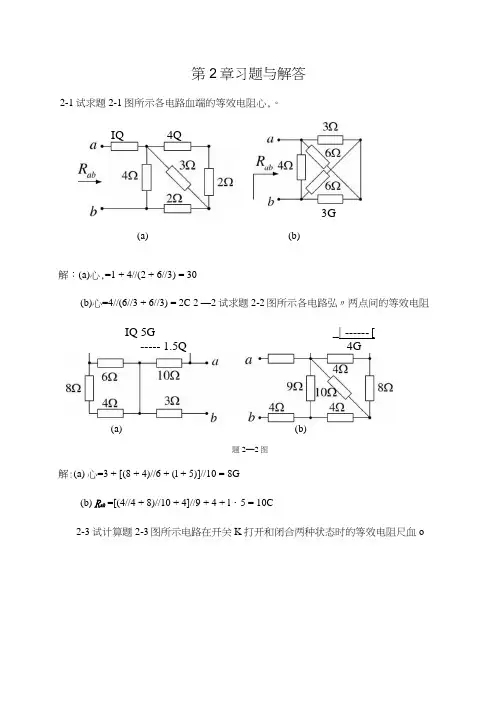
第2章习题与解答2-1试求题2-1图所示各电路血端的等效电阻心,。

解：(a)心,=1 + 4//(2 + 6//3) = 30(b)心=4//(6//3 + 6//3) = 2C 2 —2试求题2-2图所示各电路弘〃两点间的等效电阻IQ 5G_| ------ [ ----- 1.5Q 4G(a)(b)题2—2图解:(a) 心=3 + [(8 + 4)//6 + (l + 5)]//10 = 8G(b) R ah =[(4//4 + 8)//10 + 4]//9 + 4 + l ・5 = 10C2-3试计算题2-3图所示电路在开关K 打开和闭合两种状态时的等效电阻尺血oIQ 4Q3G(b)(a)题2—3图 解：(a)开关打开时心=(8 + 4)//4 = 3。

开关闭合时^,=4/74 = 20(b)开关打开时 R ah =(6 + 12)/7(6+12) = 90开关闭合时心=6//12 + 6//12 = 8。

2—4试求题2—4图(a)所示电路的电流/及题2—4图(b)所示电路的电压U 。

解：(a)从左往右流过1G 电阻的电流为I] =21/(1 + 6//12 + 3//6)二21/(l+4 + 2) = 3A 从上往下流过3 O 电阻的电流为I.= —x3 = 2A3 + 6 从上往下流过120电阻的电流为I p =—^-x3 = lA12 + 6 所以1 =【3叫2 = 1 A⑹从下往上流过6V 电压源的电流为"击莎1Q + O1V3Q 6Q(a)12Q6Q题2—4图从上往下流过两条并联支路的电流分别为2A所以U = 2x2-lx2=2V2 — 5试求题2 — 5图所示各电路ab端的等效电阻R ah,其中/?] = = 1。

2Q题2-5图解：(a)如图，对原电路做厶-丫变换后，得一平衡电桥所以心,=(*+*)//(1 + 1)= *°(b)将图中的两个Y形变成△形，如图所示2.5Q5Q 白804Q 4QT50T T2Q即得所以陰=L269G2 —6计算题2 —6图所示电路中弘b两点间的等效电阻。

第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念，电路等效变换的方法是电路问题分析中经常使用的方法。

所谓两个电路是互为等效的，是指（1）两个结构参数不同的电路再端子上有相同的电压、电流关系，因而可以互相代换；（2）代换的效果是不改变外电路（或电路中未被代换的部分）中的电压、电流和功率。

由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。

等效的对象是外接电路（或电路未变化部分）中的电压、电流和功率。

等效变换的目的是简化电路，方便地求出需要求的结果。

深刻地理解“等效变换”的思想，熟练掌握“等效变换”的方法在电路分析中是重要的。

2-1 电路如图所示，已知12100,2,8s u V R k R k ==Ω=Ω。

若：（1）38R k =Ω；（2）处开路）33(R R ∞=；（3）处短路）33(0R R =。

试求以上3种情况下电压2u 和电流23,i i 。

解：（1）2R 和3R 为并联，其等效电阻84R k ==Ω，则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==（2）当∞=3R ，有03=imA u i s 10100212===V i R u 80108222=⨯==（3）03=R ，有0,022==u imA R u i s 50210013===2-2 电路如图所示，其中电阻、电压源和电流源均为已知，且为正值。

求：（1）电压2u 和电流2i ；（2）若电阻1R 增大，对哪些元件的电压、电流有影响？影响如何？解：（1）对于2R 和3R 来说，其余部分的电路可以用电流源s i 等效代换，如题解图（a ）所示。

因此有 32332R R i R i += 32322R R i R R u s+=（2）由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源，如题解图（b ）所示。

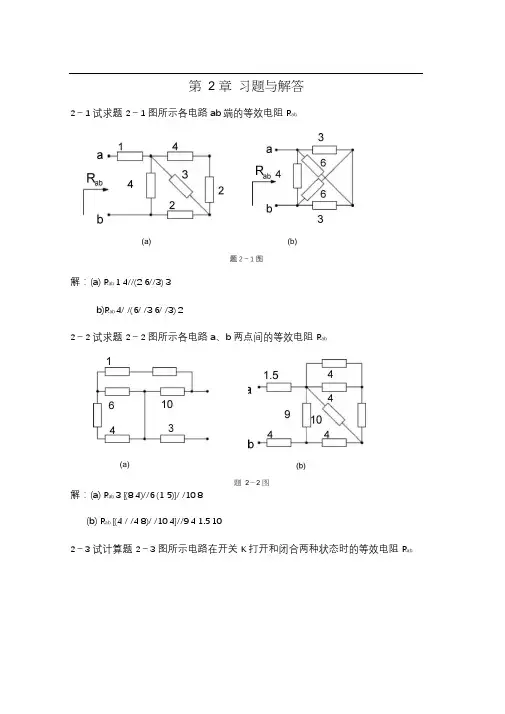
第 2 章习题与解答2－1试求题2－1图所示各电路ab端的等效电阻R ab题2－1 图解：(a) R ab 1 4//(2 6//3) 3b)R ab 4/ /(6/ /3 6/ /3) 22－2试求题2－2图所示各电路a、b两点间的等效电阻R ab解：(a) R ab 3 [(8 4)//6 (1 5)]/ /10 8(b) R ab [(4 / /4 8)/ /10 4]//9 4 1.5 102－3试计算题2－3图所示电路在开关K 打开和闭合两种状态时的等效电阻R ab(a)(b)1(a)题2－2 图解：（a）开关打开时R ab （8 4）/ /4 3开关闭合时R ab 4//4 2b）开关打开时R ab(6 12) / /(6 12) 9开关闭合时R ab6//12 6/ /12 8题2－4 图解：（a）从左往右流过1电阻的电流为I1 21/ (1 6/ /12 3 / /6)=21/ (1 42) 3A从上往下流过3电阻的电流为I3从上往下流过12 电阻的电流为I1263 2A366 3 1A12 6所以I I3-I12 =1Ab）从下往上流过6V 电压源的电流为I1+2) // (1+2) 1.56 4A2从上往下流过两条并联支路的电流分别为2A 所以 U 2 2-12=2V2－5试求题 2－5图所示各电路 ab 端的等效电阻 R ab ，其中 R 1 R 2 1b ）将图中的两个 Y 形变成△形，如图所示2.58445即得2(b)题 2－5 图1 11所以 R ab （ 1 1）/（/ 1 1） 1ab3 3 2所以R ab 1.269解：（a）将图中的Y 形变成△形，如图所示所以R ab 12//6 4b）将图中的Y 形变成△形，如图所示209402140382－6计算题2－6图所示电路中a8888 8 8b(a)12所以R ab 3/ /4 122－7 对题2－7 图所示电路，应用Y—△等效变换求电路ab 端的等效电阻角线电压U 及总电压U ab 。

电路答案——本资料由张纪光编辑整理（C2-241 内部专用）第一章电路模型和电路定律【题 1】：由UAB 5 V可得： I AC 2.5A： U DB0 ： U S12.5V。

【题 2】： D。

【题 3】： 300； -100 。

【题 4】： D。

【题5】：a i i1i 2；b u u1u2；c u u S i i S R S；d i i S 1R Su u S。

【题 6】： 3；-5 ； -8。

【题 7】： D。

【题 8】：P US150 W ；P US26W；P US30 ； P IS115 W ； P IS214W ；P IS315W。

【题 9】： C。

【题 10】：3； -3 。

【题 11】：-5 ； -13 。

【题 12】：4（吸收）； 25。

【题 13】：0.4 。

【题 14】：31I 2 3； I 1A 。

3【题 15】：I43A； I23A； I31A； I5 4 A。

【题 16】：I7A；U35 V；X元件吸收的功率为 P UI245W。

【题 17】：由图可得U EB 4 V；流过 2电阻的电流 I EB 2 A；由回路ADEBCA列KVL得U AC 2 3I ；又由节点D列KCL得 I CD 4I ；由回路CDEC列KVL解得；I 3 ；代入上式，得 U AC7 V。

【题 18】：P122 I12；故 I 22； I 1I 2；P2I 221I 2⑴ KCL：4I 13I 1；I 18；U S 2I1 1 I 18V或16.V；或I I。

2 5 A512⑵ KCL：4I 13I1；I18A；U S。

224 V第二章电阻电路的等效变换【题 1】：[解答 ]94A = 0.5 A ；U ab9I 4 8.5 V；I73U ab66 125. W = 7.5 W ；吸收I 12 1.25 A；P功率 7.5W。

【题 2】：[解答 ]【题 3】：[解答]C 。

【题 4】： [ 解答 ]等效电路如图所示，I 005. A。

2-1、求电路的入端电阻R AB 。

R= 2//2+4//6AB答案 3.4Ω2-2、求各电路的入端电阻R AB。

(6//6+9)//102-3、求各电路的入端电阻R AB。

→解：（a）(3//6+1)//6=2Ω(b) 等效电路如图所示：即2-4、试求下图所示电路中的电流I。

答案-1.1A2-5、求图示电路中的电流i。

答案：- 0.1A2-6、电路如图所示，求B点的电位V B。

解：该电路图可以改变成如下图所示的形式2-7、电路如图所示，求电流I和电压U AB。

解：原电路可以等效变换为如下电路152-8、电路如图所示，求AB端的等效电阻R AB。

解：在AB端外加电源，使u、i对二端电路来说是关联参考方向。

由图可得：得到2-9、求图 (a) 和 (b) 所示两电路的输入电阻。

2-10、用电源等效变换法求图示电路中负载R L 上的电压U 。

12A5ΩR L+ -14V +-4Ω14-2Ω 2Ω2Ω2-11、化简为一个等效的电压源支路。

(a) (b) (c) (d)其中111R U I S S =，222R U I S S =，21S S S I I I +=，)(2121R R R R R S +=，S S S I R U =。

恒流源与恒压源的串联和并联两种情况(1) (2)2-12、化简图示电路。

(a) (b) (c) (d)2-13、在图（a ）所示电路中，已知V 12=S U ，Ω=31R ，A 5=S I ，Ω=62R ，试求2R 支路中的电流2I 。

(a) (b) (c)解： 3)5312(633)(12112=++=++=S S I R U R R R I A10；2-14、在图示电路中，N为一个实际的直流电源。

当开关S断开时，电压表读数为V1。

试求该直流电源N的电压源模型与电流源模型。

当开关S闭合时，电流表读数为A解：等效电路如图：，2-15、电路如图所示。

已知Ω=61R ，Ω=1.02R ，98.0=α，Ω=53R ，V U 9.4=。

精心整理第2章习题与解答2－1试求题2－1图所示各电路ab 端的等效电阻ab R 。

(a) (b)题2－1图解：（a ）14//(26//3)3ab R =++=Ω（b 2－2解：（a （b 2－3(a)(b)解：（a （b 2－4(a) (b)题2－4图解：（a ）从左往右流过1Ω电阻的电流为从上往下流过3Ω电阻的电流为36I 32A 36=⨯=+ 从上往下流过12Ω电阻的电流为126I 31A 126=⨯=+ 所以312I I -I =1A =（b ）从下往上流过6V 电压源的电流为66I 4A 1.5===（1+2）//（1+2） 从上往下流过两条并联支路的电流分别为2A所以U 22-12=2V =⨯⨯2－5试求题2－5图所示各电路ab 端的等效电阻ab R ，其中121R R ==Ω。

(a) (b)题2－5图解：（a（b 即得所以ab R 2－6解：（a 所以ab R （b 所以ab R 2－7U 及总电压ab U 题2－7图解：将图中的Y 形变成△形，如图所示所以(32.5//526//2)//2655510ab R =++=+=Ω回到原图已知128I I +=348I I +=1310840I I +=245240I I +=联立解得1 2.4I A =2 5.6I A =32I A =46I A =所以121054U I I V =-+=2－8试求题2－8图所示电路的输入电阻in R 。

(a)(b)题2－8图解：（a ）如图所示，在电路端口加电压源U ，求I 所以21(1)in U R R R Iμ==+- （b ）如图所示，在电路端口加电压源U ，求I12R R U 2－（b 2－62－题2－11图解：先化简电路，如图所示43Ω所以有41(2933i i +-=3i A = 2－12题2－12图所示电路中全部电阻均为1Ω，试求电路中的电流i 。

题2－12图解：先求电路右边电阻块的等效电阻ab R ，如图所示将中间的Y 形化成△形。

第2章 习题与解答2－1试求题2－1图所示各电路ab 端的等效电阻ab R 。

2Ω3Ω(a)(b)题2－1图解：（a ）14//(26//3)3ab R =++=Ω （b ）4//(6//36//3)2ab R =+=Ω2－2试求题2－2图所示各电路a b 、两点间的等效电阻ab R 。

ab8Ωab8Ω(a)(b)题2－2图解：（a ）3[(84)//6(15)]//108ab R =++++=Ω （b ）[(4//48)//104]//94 1.510ab R =++++=Ω2－3试计算题2－3图所示电路在开关K 打开和闭合两种状态时的等效电阻ab R 。

8Ωab(a) (b)题2－3图解：（a ）开关打开时(84)//43ab R =+=Ω开关闭合时4//42ab R ==Ω（b ）开关打开时(612)//(612)9ab R =++=Ω开关闭合时6//126//128ab R =+=Ω2－4试求题2－4图（a ）所示电路的电流I 及题2－4图（b ）所示电路的电压U 。

6Ω6Ω(a) (b)题2－4图解：（a ）从左往右流过1Ω电阻的电流为1I 21/(16//123//621/(142)3A =++++=）=从上往下流过3Ω电阻的电流为36I 32A 36=⨯=+ 从上往下流过12Ω电阻的电流为126I 31A 126=⨯=+ 所以 312I I -I =1A =（b ）从下往上流过6V 电压源的电流为 66I 4A 1.5===（1+2）//（1+2）从上往下流过两条并联支路的电流分别为2A 所以 U 22-12=2V =⨯⨯2－5试求题2－5图所示各电路ab 端的等效电阻ab R ，其中121R R ==Ω。

2Ω(a)(b)题2－5图解：（a ）如图，对原电路做△-Y 变换后，得一平衡电桥1a所以 111//11332ab R =++=Ω（）（）（b ）将图中的两个Y 形变成△形，如图所示2Ωab即得4021Ωab所以 1.269ab R =Ω2－6计算题2－6图所示电路中a b 、两点间的等效电阻。

第二章(电阻电路的等效变换)习题解答一、选择题1．在图2—1所示电路中，电压源发出的功率为 B 。

A ．4W ；B ．3-W ；C ．3W ；D ．4-W2．在图2—2所示电路中，电阻2R 增加时，电流I 将 A 。

A ．增加；B ．减小；C ．不变；D ．不能确定3．在图2—3所示电路中，1I = D 。

A ．5.0A ；B ．1-A ；C ．5.1A ；D ．2A4．对于图2—4所示电路，就外特性而言，则 D 。

A ． a 、b 等效； B ． a 、d 等效； C ． a 、b 、c 、d 均等效； D ． b 、c 等效5．在图2—5所示电路中，N 为纯电阻网络，对于此电路，有 C 。

A ．S S I U 、都发出功率； B ．S S I U 、都吸收功率； C ．S I 发出功率，S U 不一定； D ．S U 发出功率，S I 不一定二、填空题1． 图2—6（a ）所示电路与图2—6（b ）所示电路等效，则在图2—6（b ）所示电路中，6=S U V ，Ω=2R 。

2．图2—7（a ）所示电路与图2—7（b ）所示电路等效，则在图2—7（b ）所示电路中，1=S I A ,Ω=2R 。

3．在图2—8所示电路中，输入电阻Ω=2ab R 。

4．在图2—9所示电路中，受控源发出的功率是30-W 。

5．在图2—10所示电路中，2A 电流源吸收的功率是20-W 。

三、计算题1．对于图2—11所示电路，试求：1)．电压1U 、2U ；2)．各电源的功率， 并指出是吸收还是发出。

解：21=U V ， 3132-=-⨯=)(U V 621122=⨯+=)(V P W (发出)，11221-=⨯+=)(U P A W (吸收1-W ，发出１W) 2．计算图2—12所示电路中的电流I 。

解：将图2—12所示电路中Ω1电阻和Ω2电阻的串联用Ω3的电阻等效，将4A 电流源和Ω3电阻的并联用12V 电压源和Ω3电阻的串联等效，可得图2—12所示电路的等效电路如图2—12（a ）。