浙江大学835材料力学(乙)历年考研试题
- 格式:pdf
- 大小:1.92 MB
- 文档页数:13

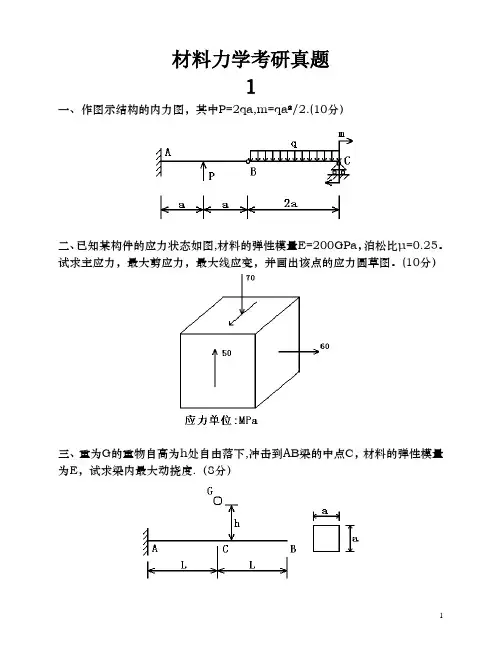
材料力学考研真题1一、作图示结构的内力图,其中P=2qa,m=qa²/2.(10分)二、已知某构件的应力状态如图,材料的弹性模量E=200GPa,泊松比µ=0.25。
试求主应力,最大剪应力,最大线应变,并画出该点的应力圆草图。
(10分)三、重为G的重物自高为h处自由落下,冲击到AB梁的中点C,材料的弹性模量为E,试求梁内最大动挠度.(8分)四、钢制平面直角曲拐ABC,受力如图。
q=2。
5πKN/m,AB段为圆截面,[σ]=160MPa,设L=10d,P x=qL,试设计AB段的直径d。
(15分)五、图示钢架,EI为常数,试求铰链C左右两截面的相对转角(不计轴力及剪力对变形的影响)。
(12分)六、图示梁由三块等厚木板胶合而成,载荷P可以在ABC梁上移动。
已知板的许用弯曲正应力为[σ]=10Mpa,许用剪应力[τ]=1Mpa,胶合面上的许用剪应力[τ]胶=0.34Mpa,a=1m,b=10cm,h=5cm,试求许可荷载[P].(10分)七、图示一转臂起重机架ABC ,其中AB 为空心圆截面杆D=76mm ,d=68mm,BC 为实心圆截面杆D 1=20mm ,两杆材料相同,σp =200Mpa ,σs =235Mpa ,E=206Gpa 。
取强度安全系数n=1。
5,稳定安全系数n st =4。
最大起重量G=20KN ,临界应力经验公式为σcr =304—1。
12λ(Mpa )。
试校核此结构。
(15分)八、水平曲拐ABC 为圆截面杆,在C 段上方有一铅垂杆DK ,制造时DK 杆短了△.曲拐AB 和BC 段的抗扭刚度和抗弯刚度皆为GI P 和EI 。
且GI P =45EI 。
杆DK 抗拉刚度为EA,且EA=225EIa。
试求:(1)在AB 段杆的B 端加多大扭矩,才可使C 点刚好与D 点相接触? (2)若C 、D 两点相接触后,用铰链将C 、D 两点连在一起,在逐渐撤除所加扭矩,求DK 杆内的轴力和固定端处A 截面上的内力。

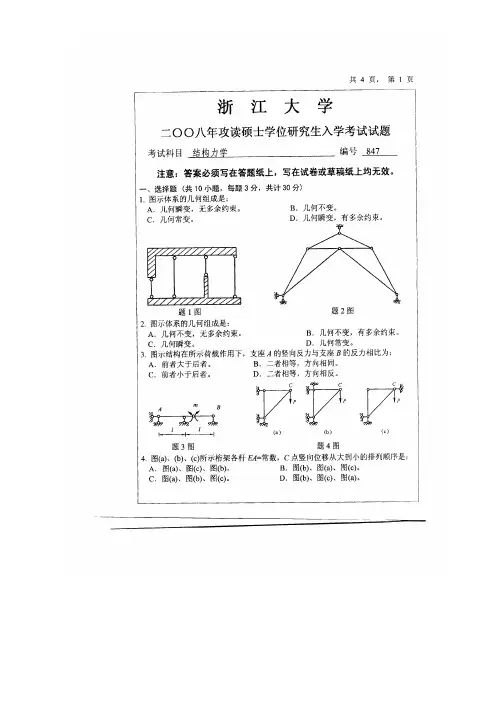
浙江大学材料力学甲考研真题一、选择题1. 下列选项中,具有永久变形的固体是()A. 弹性体B. 塑性体C. 刚性体D. 电介质2. 在应力应变曲线中,弹性阶段表征了材料的()A. 刚度B. 韧性C. 脆性D. 可塑性3. 在材料拉伸实验中,杨氏模量的计算公式为()A. E = σ/εB. E = F/AC. E = kxD. E = mg4. 下列变形方式中,不属于蠕变变形的是()A. 弯曲变形B. 拉伸变形C. 剪切变形D. 压缩变形5. 在材料力学中,疲劳破坏主要是由于()A. 高温作用B. 强烈的冲击C. 长期受载D. 变形过程中的变温二、填空题1. 材料的刚度可以用______来表示。
2. 断裂韧性是材料断裂过程中吸收的_____能量。
3. 杨氏模量是材料在____方向上的刚度。
4. 材料塑性变形的临界应力称为_____。
5. 蠕变试验是材料的_____性能的一种试验方法。
三、问答题1. 简述弹性体和塑性体的区别。
弹性体和塑性体是固体材料的两种基本变形方式。
弹性体是指在受力作用下可以发生弹性变形的物质。
弹性体的应变与应力之间的关系满足线性弹性关系,也即应力与应变成正比。
一旦外力撤去,弹性体会恢复原来的形状和大小。
而塑性体是指在受力作用下会发生永久性变形的物质。
塑性体的应变与应力之间的关系不满足线性关系。
一旦外力撤去,塑性体会保持变形状态。
2. 什么是杨氏模量?如何计算?杨氏模量是材料在拉伸过程中应力与应变之间的比值。
杨氏模量可以用于描述材料的刚度,也即材料在受力作用下变形的程度。
计算材料的杨氏模量时,可以通过材料在拉伸试验中的应力与应变的比值得到。
3. 什么是材料的蠕变特性?该如何进行蠕变试验?材料的蠕变特性是材料在长时间持续受力作用下,随时间变化而发生的变形现象。
材料的蠕变特性与应力、温度、时间等因素都有关。
蠕变试验是研究材料蠕变特性的一种方法。
在蠕变试验中,常常使用恒定应力或恒定应变的加载方式,来观察材料在长时间加载过程中的变形情况。

材料力学考研真题1一、作图示结构的内力图,其中P=2qa,m=qa²/2。
(10分)二、已知某构件的应力状态如图,材料的弹性模量E=200GPa,泊松比µ=0.25。
试求主应力,最大剪应力,最大线应变,并画出该点的应力圆草图。
(10分)三、重为G的重物自高为h处自由落下,冲击到AB梁的中点C,材料的弹性模量为E,试求梁内最大动挠度。
(8分)四、钢制平面直角曲拐ABC,受力如图。
q=2.5πKN/m,AB段为圆截面,[σ]=160MPa,设L=10d,P x=qL,试设计AB段的直径d。
(15分)五、图示钢架,EI为常数,试求铰链C左右两截面的相对转角(不计轴力及剪力对变形的影响)。
(12分)六、图示梁由三块等厚木板胶合而成,载荷P可以在ABC梁上移动。
已知板的许用弯曲正应力为[σ]=10Mpa,许用剪应力[τ]=1Mpa,胶合面上的许用剪应力[τ]胶=0.34Mpa,a=1m,b=10cm,h=5cm,试求许可荷载[P]。
(10分)七、图示一转臂起重机架ABC,其中AB为空心圆截面杆D=76mm,d=68mm,BC为实心圆截面杆D 1=20mm ,两杆材料相同,σp =200Mpa ,σs =235Mpa ,E=206Gpa 。
取强度安全系数n=1.5,稳定安全系数n st =4。
最大起重量G=20KN ,临界应力经验公式为σcr =304-1.12λ(Mpa )。
试校核此结构。
(15分)八、水平曲拐ABC 为圆截面杆,在C 段上方有一铅垂杆DK ,制造时DK 杆短了△。
曲拐AB 和BC 段的抗扭刚度和抗弯刚度皆为GI P 和EI 。
且GI P =45EI 。
杆DK抗拉刚度为EA ,且EA=225EIa。
试求:(1)在AB 段杆的B 端加多大扭矩,才可使C 点刚好与D 点相接触?(2)若C 、D 两点相接触后,用铰链将C 、D 两点连在一起,在逐渐撤除所加扭矩,求DK 杆内的轴力和固定端处A 截面上的内力。

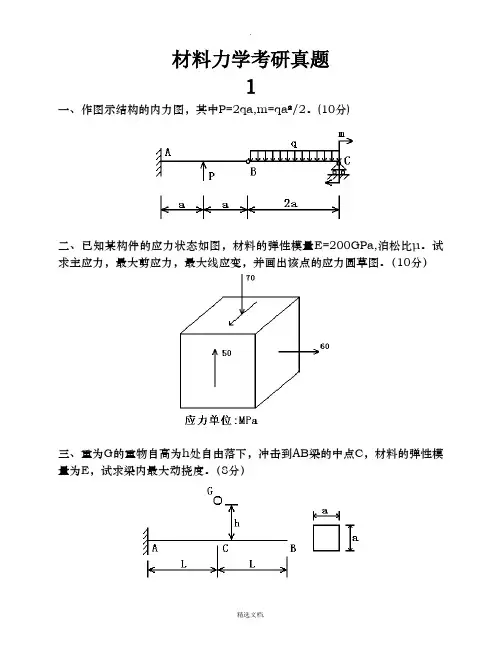
材料力学考研真题1一、作图示结构的内力图,其中P=2qa,m=qa²/2。
(10分)二、已知某构件的应力状态如图,材料的弹性模量E=200GPa,泊松比µ。
试求主应力,最大剪应力,最大线应变,并画出该点的应力圆草图。
(10分)三、重为G的重物自高为h处自由落下,冲击到AB梁的中点C,材料的弹性模量为E,试求梁内最大动挠度。
(8分)四、钢制平面直角曲拐ABC,受力如图。
πKN/m,AB段为圆截面,[σ]=160MPa,设L=10d,P x=qL,试设计AB段的直径d。
(15分)五、图示钢架,EI为常数,试求铰链C左右两截面的相对转角(不计轴力及剪力对变形的影响)。
(12分)六、图示梁由三块等厚木板胶合而成,载荷P可以在ABC梁上移动。
已知板的许用弯曲正应力为[σ]=10Mpa,许用剪应力[τ]=1Mpa,胶合面上的许用剪应力[τ]胶=0.34Mpa,a=1m,b=10cm,h=5cm,试求许可荷载[P]。
(10分)七、图示一转臂起重机架ABC ,其中AB 为空心圆截面杆D=76mm ,d=68mm ,BC 为实心圆截面杆D 1=20mm ,两杆材料相同,σp =200Mpa ,σs =235Mpa ,E=206Gpa 。
取强度安全系数n=1.5,稳定安全系数n st =4。
最大起重量G=20KN ,临界应力经验公式为σcr =λ(Mpa )。
试校核此结构。
(15分)八、水平曲拐ABC 为圆截面杆,在C 段上方有一铅垂杆DK ,制造时DK 杆短了△。
曲拐AB 和BC 段的抗扭刚度和抗弯刚度皆为GI P 和EI 。
且GI P =45EI 。
杆DK 抗拉刚度为EA ,且EA=225EI a。
试求: (1)在AB 段杆的B 端加多大扭矩,才可使C 点刚好与D 点相接触?(2)若C 、D 两点相接触后,用铰链将C 、D 两点连在一起,在逐渐撤除所加扭矩,求DK 杆内的轴力和固定端处A 截面上的内力。

浙江工业大学816材料力学(I)2023——2023年考研真题试题试卷一、选择题1.下列属于热力学性质的是() A. 密度 B. 理想气体状态方程 C. 热传导 D. 热膨胀系数2.金属材料的拉伸过程中,断后形式为() A. 切口 B. 百叶花纹 C. 金字塔花纹 D. 斯瑞斯纹3.以下变形机械模型中,属于连续介质之机械相似机械的变形模型不包括() A. 弹性模型 B. 弹塑性模型 C. 粘弹性模型 D. 塑性模型4.材料的外延层由上至下垂直于荷载方向有() A. 压缩区、弹性层、内延层 B. 压缩区、内延层、弹性层 C. 弹性层、压缩区、内延层 D. 弹性层、内延层、压缩区5.刚度矩阵[A]是对称的,那么应力矩阵[σ]一定()A. 也是对称的B. 不一定对称C. 是一个单位矩阵D. 是一个零矩阵二、判断题1.应力张量以应变张量为前因的() A. 正 B. 否2.具有各向同性的材料的应力张量一定在某一理想坐标系中被对角化为主应力张量() A. 正 B. 否三、填空题1.静态平衡方程表达式为 _____________2.应变能密度定义为 ______________3.在应力张量三个主应力相等模式下,应力状态为_____________四、解答题1.试说明杨氏模量和抗剪强度之间的关系。
解:杨氏模量和抗剪强度是材料力学中两个重要的力学性质。
杨氏模量是刻画材料在弹性阶段的刚度,它表示单位面积内材料在线性弹性区的变形程度。
而抗剪强度则是材料抗剪切应力的能力,它是材料在屈服前能够承受的最大剪切应力。
理论上,杨氏模量和抗剪强度之间存在一定的关系。
根据弹性理论,可以得到以下关系式:$$G = \\frac{E}{2(1+\\mu)}$$其中,G为剪切模量,G为杨氏模量,$\\mu$为泊松比。
由上式可以看出,杨氏模量和抗剪强度之间的关系是通过材料的泊松比来联系的。
当泊松比接近0.5时,材料的抗剪强度会趋近于杨氏模量的一半;而当泊松比接近0或1时,材料的抗剪强度会趋近于0。